3.3 指数函数(一)学案5(含答案)
文档属性
| 名称 | 3.3 指数函数(一)学案5(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 229.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-15 00:00:00 | ||
图片预览


文档简介
3.3 指数函数(一)
学案
课时目标 1.理解指数函数的概念,会判断一个函数是否为指数函数.2.掌握指数函数的图象和性质.
1.指数函数的概念
一般地,______________________叫做指数函数,其中x是自变量,函数的定义域是____.
2.指数函数y=ax(a>0,且a≠1)的图象和性质
a>1
0图象
定义域
R
值域
(0,+∞)
性质
过定点
过点______,即x=____时,y=____
函数值的变化
当x>0时,______;当x<0时,________
当x>0时,________;当x<0时,________
单调性
是R上的________
是R上的________
一、填空题
1.下列以x为自变量的函数中,是指数函数的是______.(填序号)
①y=(-4)x;②y=πx;③y=-4x;④y=ax+2(a>0且a≠1).
2.函数f(x)=(a2-3a+3)ax是指数函数,则a的值为________.
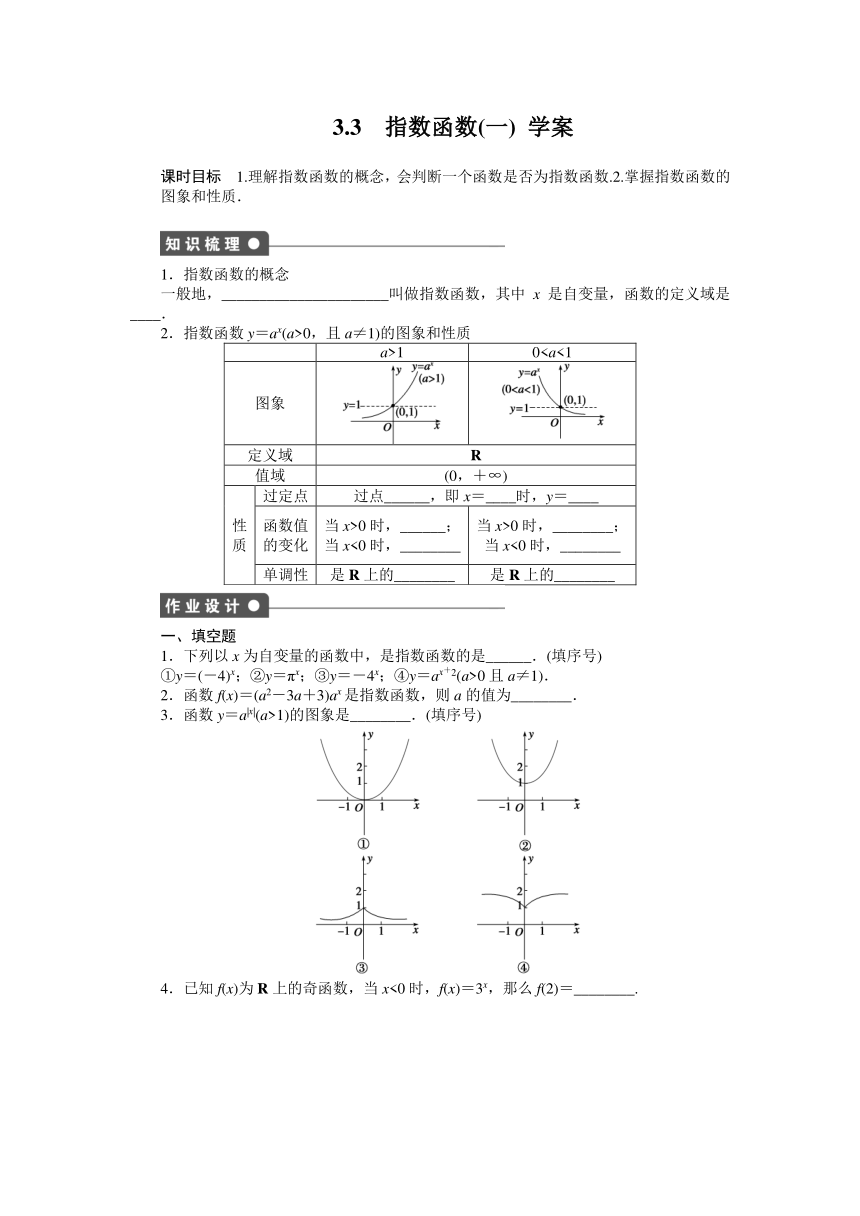
3.函数y=a|x|(a>1)的图象是________.(填序号)
4.已知f(x)为R上的奇函数,当x<0时,f(x)=3x,那么f(2)=________.
5.如图是指数函数
①y=ax;
②y=bx;
③y=cx;
④y=dx的图象,则a、b、c、d与1的大小关系是________.
6.函数y=()x-2的图象必过第________象限.
7.函数f(x)=ax的图象经过点(2,4),则f(-3)的值为____.
8.若函数y=ax-(b-1)(a>0,a≠1)的图象不经过第二象限,则a,b需满足的条件为________.
9.函数y=8-23-x(x≥0)的值域是________.
二、解答题
10.比较下列各组数中两个值的大小:
(1)0.2-1.5和0.2-1.7;
(2)和;
(3)2-1.5和30.2.
11.2000年10月18日,美国某城市的日报以醒目标题刊登了一条消息:“市政委员会今天宣布:本市垃圾的体积达到50
000
m3”,副标题是:“垃圾的体积每三年增加一倍”.如果把3年作为垃圾体积加倍的周期,请你完成下面关于垃圾的体积V(m3)与垃圾体积的加倍的周期(3年)数n的关系的表格,并回答下列问题.
周期数n
体积V(m3)
0
50
000×20
1
50
000×2
2
50
000×22
…
…
n
50
000×2n
(1)设想城市垃圾的体积每3年继续加倍,问24年后该市垃圾的体积是多少?
(2)根据报纸所述的信息,你估计3年前垃圾的体积是多少?
(3)如果n=-2,这时的n,V表示什么信息?
(4)写出n与V的函数关系式,并画出函数图象(横轴取n轴).
(5)曲线可能与横轴相交吗?为什么?
能力提升
12.定义运算a b=,则函数f(x)=1 2x的图象是________.(填序号)
13.定义在区间(0,+∞)上的函数f(x)满足对任意的实数x,y都有f(xy)=yf(x).
(1)求f(1)的值;
(2)若f()>0,解不等式f(ax)>0.(其中字母a为常数).
1.函数y=f(x)与函数y=f(-x)的图象关于y轴对称;函数y=f(x)与函数y=-f(x)的图象关于x轴对称;函数y=f(x)与函数y=-f(-x)的图象关于原点对称.
2.函数图象的平移变换是一种基本的图象变换.一般地,函数y=f(x-a)的图象可由函数y=f(x)的图象向右(a>0)或向左(a<0)平移|a|个单位得到.
3.3 指数函数(一)答案
知识梳理
1.函数y=ax(a>0,且a≠1) R 2.(0,1) 0 1 y>1
01 增函数 减函数
作业设计
1.②
解析 ①中-4<0,不满足指数函数底数的要求,③中因有负号,也不是指数函数,④中的函数可化为y=a2·ax,ax的系数不是1,故也不是指数函数.
2.2
解析 由题意得
解得a=2.
3.②
解析 该函数是偶函数.可先画出x≥0时,y=ax的图象,然后沿y轴翻折过去,便得到x<0时的函数图象.
4.-
解析 当x>0时,-x<0,∴f(-x)=3-x,
即-f(x)=()x,
∴f(x)=-()x.
因此有f(2)=-()2=-.
5.b解析 作直线x=1与四个指数函数图象交点的坐标分别为(1,a)、(1,b)、(1,c)、(1,d),由图象可知纵坐标的大小关系.
6.二、三、四
解析 函数y=()x的图象上所有的点向下平移2个单位,就得到函数y=()x-2的图象,所以观察y=()x-2的图象可知.
7.
解析 由题意a2=4,∴a=2.f(-3)=2-3=.
8.a>1,b≥2
解析 函数y=ax-(b-1)的图象可以看作由函数y=ax的图象沿y轴平移|b-1|个单位得到.若01时,由于y=ax的图象必过定点(0,1),当y=ax的图象沿y轴向下平移1个单位后,得到的图象不经过第二象限.由b-1≥1,得b≥2.因此,a,b必满足条件a>1,b≥2.
9.[0,8)
解析 y=8-23-x=8-23·2-x=8-8·()x
=8[1-()x].
∵x≥0,∴0<()x≤1,∴-1≤-()x<0,
从而有0≤1-()x<1,因此0≤y<8.
10.解 (1)考察函数y=0.2x.
因为0<0.2<1,
所以函数y=0.2x在实数集R上是单调减函数.
又因为-1.5>-1.7,所以0.2-1.5<0.2-1.7.
(2)考察函数y=()x.因为0<<1,
所以函数y=()x在实数集R上是单调减函数.
又因为<,所以>1.
(3)2-1.5<20,即2-1.5<1;30<30.2,
即1<30.2,所以2-1.5<30.2.
11.解 (1)由于垃圾的体积每3年增加1倍,24年后即8个周期后,该市垃圾的体积是50
000×28=12
800
000(m3).
(2)根据报纸所述的信息,估计3年前垃圾的体积是50
000×2-1=25
000(m3).
(3)如果n=-2,这时的n表示6年前,V表示6年前垃圾的体积.
(4)n与V的函数关系式是V=50
000×2n,图象如图所示.
(5)因为对任意的整数n,2n>0,所以V=50
000×2n>0,因此曲线不可能与横轴相交.
12.①
解析 由题意f(x)=1 2x=
13.解 (1)令x=1,y=2,可知f(1)=2f(1),故f(1)=0.
(2)设0且s>t,又f()>0,
∴f(x1)-f(x2)=f[()s]-f[()t]
=sf()-tf()=(s-t)f()>0,
∴f(x1)>f(x2).
故f(x)在(0,+∞)上是减函数.
又∵f(ax)>0,x>0,f(1)=0,
∴0当a=0时,x∈ ,
当a>0时,0当a<0时,综上:a≤0时,x∈ ;
a>0时,不等式解集为{x|0
学案
课时目标 1.理解指数函数的概念,会判断一个函数是否为指数函数.2.掌握指数函数的图象和性质.
1.指数函数的概念
一般地,______________________叫做指数函数,其中x是自变量,函数的定义域是____.
2.指数函数y=ax(a>0,且a≠1)的图象和性质
a>1
0
定义域
R
值域
(0,+∞)
性质
过定点
过点______,即x=____时,y=____
函数值的变化
当x>0时,______;当x<0时,________
当x>0时,________;当x<0时,________
单调性
是R上的________
是R上的________
一、填空题
1.下列以x为自变量的函数中,是指数函数的是______.(填序号)
①y=(-4)x;②y=πx;③y=-4x;④y=ax+2(a>0且a≠1).
2.函数f(x)=(a2-3a+3)ax是指数函数,则a的值为________.
3.函数y=a|x|(a>1)的图象是________.(填序号)
4.已知f(x)为R上的奇函数,当x<0时,f(x)=3x,那么f(2)=________.
5.如图是指数函数
①y=ax;
②y=bx;
③y=cx;
④y=dx的图象,则a、b、c、d与1的大小关系是________.
6.函数y=()x-2的图象必过第________象限.
7.函数f(x)=ax的图象经过点(2,4),则f(-3)的值为____.
8.若函数y=ax-(b-1)(a>0,a≠1)的图象不经过第二象限,则a,b需满足的条件为________.
9.函数y=8-23-x(x≥0)的值域是________.
二、解答题
10.比较下列各组数中两个值的大小:
(1)0.2-1.5和0.2-1.7;
(2)和;
(3)2-1.5和30.2.
11.2000年10月18日,美国某城市的日报以醒目标题刊登了一条消息:“市政委员会今天宣布:本市垃圾的体积达到50
000
m3”,副标题是:“垃圾的体积每三年增加一倍”.如果把3年作为垃圾体积加倍的周期,请你完成下面关于垃圾的体积V(m3)与垃圾体积的加倍的周期(3年)数n的关系的表格,并回答下列问题.
周期数n
体积V(m3)
0
50
000×20
1
50
000×2
2
50
000×22
…
…
n
50
000×2n
(1)设想城市垃圾的体积每3年继续加倍,问24年后该市垃圾的体积是多少?
(2)根据报纸所述的信息,你估计3年前垃圾的体积是多少?
(3)如果n=-2,这时的n,V表示什么信息?
(4)写出n与V的函数关系式,并画出函数图象(横轴取n轴).
(5)曲线可能与横轴相交吗?为什么?
能力提升
12.定义运算a b=,则函数f(x)=1 2x的图象是________.(填序号)
13.定义在区间(0,+∞)上的函数f(x)满足对任意的实数x,y都有f(xy)=yf(x).
(1)求f(1)的值;
(2)若f()>0,解不等式f(ax)>0.(其中字母a为常数).
1.函数y=f(x)与函数y=f(-x)的图象关于y轴对称;函数y=f(x)与函数y=-f(x)的图象关于x轴对称;函数y=f(x)与函数y=-f(-x)的图象关于原点对称.
2.函数图象的平移变换是一种基本的图象变换.一般地,函数y=f(x-a)的图象可由函数y=f(x)的图象向右(a>0)或向左(a<0)平移|a|个单位得到.
3.3 指数函数(一)答案
知识梳理
1.函数y=ax(a>0,且a≠1) R 2.(0,1) 0 1 y>1
0
作业设计
1.②
解析 ①中-4<0,不满足指数函数底数的要求,③中因有负号,也不是指数函数,④中的函数可化为y=a2·ax,ax的系数不是1,故也不是指数函数.
2.2
解析 由题意得
解得a=2.
3.②
解析 该函数是偶函数.可先画出x≥0时,y=ax的图象,然后沿y轴翻折过去,便得到x<0时的函数图象.
4.-
解析 当x>0时,-x<0,∴f(-x)=3-x,
即-f(x)=()x,
∴f(x)=-()x.
因此有f(2)=-()2=-.
5.b
6.二、三、四
解析 函数y=()x的图象上所有的点向下平移2个单位,就得到函数y=()x-2的图象,所以观察y=()x-2的图象可知.
7.
解析 由题意a2=4,∴a=2.f(-3)=2-3=.
8.a>1,b≥2
解析 函数y=ax-(b-1)的图象可以看作由函数y=ax的图象沿y轴平移|b-1|个单位得到.若0
9.[0,8)
解析 y=8-23-x=8-23·2-x=8-8·()x
=8[1-()x].
∵x≥0,∴0<()x≤1,∴-1≤-()x<0,
从而有0≤1-()x<1,因此0≤y<8.
10.解 (1)考察函数y=0.2x.
因为0<0.2<1,
所以函数y=0.2x在实数集R上是单调减函数.
又因为-1.5>-1.7,所以0.2-1.5<0.2-1.7.
(2)考察函数y=()x.因为0<<1,
所以函数y=()x在实数集R上是单调减函数.
又因为<,所以>1.
(3)2-1.5<20,即2-1.5<1;30<30.2,
即1<30.2,所以2-1.5<30.2.
11.解 (1)由于垃圾的体积每3年增加1倍,24年后即8个周期后,该市垃圾的体积是50
000×28=12
800
000(m3).
(2)根据报纸所述的信息,估计3年前垃圾的体积是50
000×2-1=25
000(m3).
(3)如果n=-2,这时的n表示6年前,V表示6年前垃圾的体积.
(4)n与V的函数关系式是V=50
000×2n,图象如图所示.
(5)因为对任意的整数n,2n>0,所以V=50
000×2n>0,因此曲线不可能与横轴相交.
12.①
解析 由题意f(x)=1 2x=
13.解 (1)令x=1,y=2,可知f(1)=2f(1),故f(1)=0.
(2)设0
∴f(x1)-f(x2)=f[()s]-f[()t]
=sf()-tf()=(s-t)f()>0,
∴f(x1)>f(x2).
故f(x)在(0,+∞)上是减函数.
又∵f(ax)>0,x>0,f(1)=0,
∴0
当a>0时,0
a>0时,不等式解集为{x|0
