3.3.2 指数函数的图像与性质的应用 学案1(含答案)
文档属性
| 名称 | 3.3.2 指数函数的图像与性质的应用 学案1(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-15 22:10:28 | ||
图片预览




文档简介
3.3.2
指数函数的图像与性质的应用
学案
课标解读
1.理解并掌握指数函数的图像和性质.(重点)2.掌握函数图像的简单变换.(易混点)3.能运用指数函数的有关性质去研究指数型函数的性质.(难点)
知识
函数图像的变换
【问题导思】
若已知函数f(x)=2x的图像.
1.如何得到f(x)=2x-1的图像?
【提示】 向右平移1个单位.
2.如何得到f(x)=2x-2的图像?
【提示】 向下平移2个单位.
3.如何得到f(x)=()x的图像?
【提示】 作f(x)=2x关于y轴的对称图像.
4.如何得到f(x)=-2x的图像?
【提示】 将f(x)=2x的图像以x轴为对称轴翻折到x轴下方.
1.平移变换
(1)左右平移:y=f(x)y=f(x+a)
特征:左加右减:
(2)上下平移:y=f(x)y=f(x)+k
特征:上加下减.
2.对称变换
(1)y=f(x)y=-f(x);
(2)y=f(x)y=f(-x);
(3)y=f(x)y=-f(-x).
3.翻折变换
(1)y=f(x)
y=f(|x|).
(2)y=f(x)
Y=|f(x)|
(见学生用书第43页)
类型1
函数图像的作法
利用函数f(x)=()x的图像,作出下列函数的图像:
(1)f(x+1);(2)-f(x);(3)f(-x).
【思路探究】 作出y=()x
的图像→明确f(x)与f(x+1),
-f(x),f(-x)图像间
的关系
分别得出图像
【自主解答】 作出f(x)=()x的图像,如图所示:
(1)f(x+1)的图像:需将f(x)的图像向左平移1个单位得f(x+1)的图像,如图(1).
(2)-f(x)的图像:作f(x)的图像关于x轴对称的图像得-f(x)的图像,如图(2).
(3)f(-x)的图像:作f(x)的图像关于y轴对称的图像得f(-x)的图像,如图(3).
1.利用已知的函数图像作图,主要运用图像的平移、对称等变换,平移变换需分清楚向何方向移,要移多少个单位,如(1);对称变换需分清对称轴是什么,如(2)(3).
2.利用变换作图,一般步骤是:
选基函数→写出变换过程→画图像
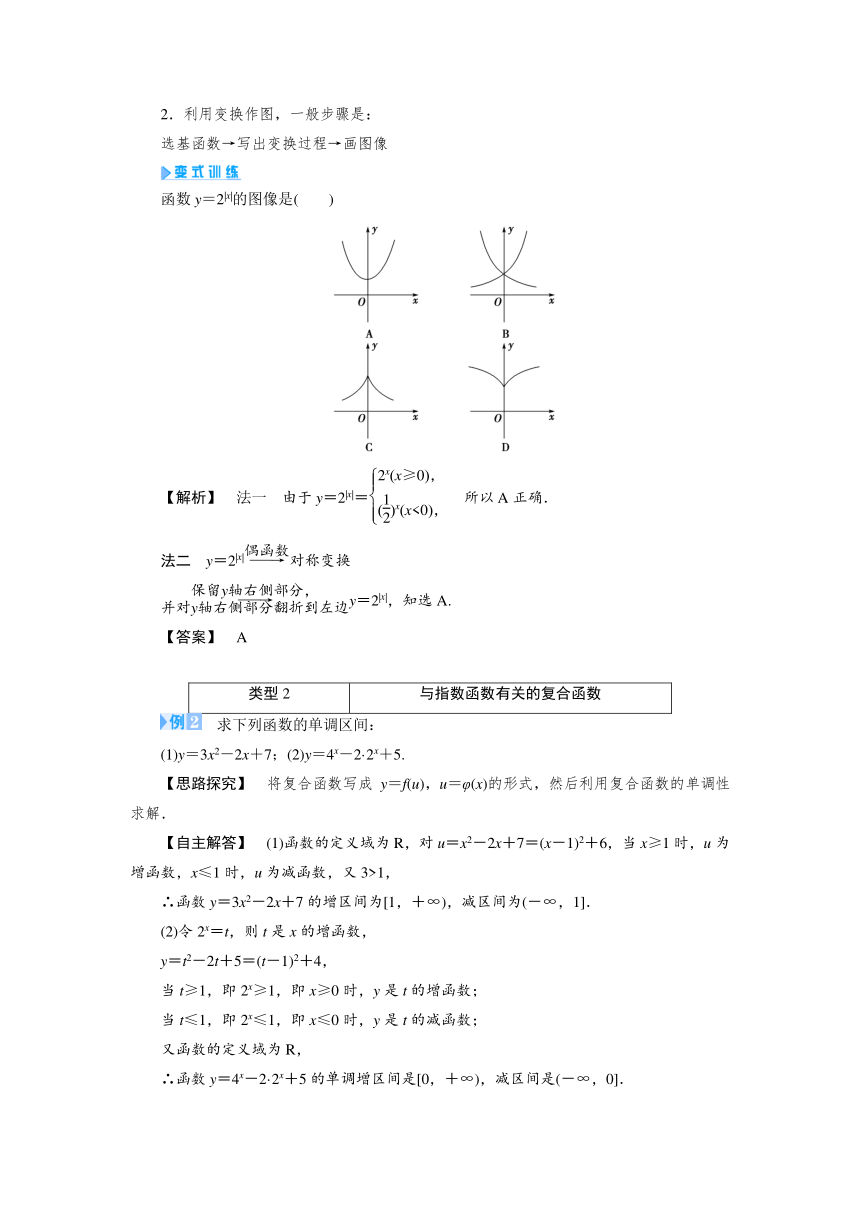
函数y=2|x|的图像是( )
【解析】 法一 由于y=2|x|=所以A正确.
法二 y=2|x|对称变换
y=2|x|,知选A.
【答案】 A
类型2
与指数函数有关的复合函数
求下列函数的单调区间:
(1)y=3x2-2x+7;(2)y=4x-2·2x+5.
【思路探究】 将复合函数写成y=f(u),u=φ(x)的形式,然后利用复合函数的单调性求解.
【自主解答】 (1)函数的定义域为R,对u=x2-2x+7=(x-1)2+6,当x≥1时,u为增函数,x≤1时,u为减函数,又3>1,
∴函数y=3x2-2x+7的增区间为[1,+∞),减区间为(-∞,1].
(2)令2x=t,则t是x的增函数,
y=t2-2t+5=(t-1)2+4,
当t≥1,即2x≥1,即x≥0时,y是t的增函数;
当t≤1,即2x≤1,即x≤0时,y是t的减函数;
又函数的定义域为R,
∴函数y=4x-2·2x+5的单调增区间是[0,+∞),减区间是(-∞,0].
1.求函数的单调区间,首先求函数的定义域,对复合函数的单调性,应注意y=f(u)与u=g(x)单调性的一致性和相反性.
2.在复合函数中,一般情况下,如果两个函数都是增函数或都是减函数,则复合函数是增函数;如果两个函数一增一减,则复合函数为减函数,简称“同增异减”.
(1)(2013·荆州检测)函数y=()x2-3x+2的单调增区间是________.
(2)y=(-1)-x2+2x+3的单调增区间是( )
A.(1,+∞) B.(-∞,1]
C.(1,3)
D.(-1,1)
【解析】 令u=x2-3x+2=(x-)2-,令y=()u在定义域内是减函数,而求y=()x2-3x+2的增区间,只需求u的减区间,∴x∈(-∞,].
(2)函数y的定义域为R,u=-x2+2x+3=-(x-1)2+4;x≥1时,u是减函数,又0<-1<1,
∴y的增区间为(1,+∞).
【答案】 (1)(-∞,] (2)A
类型3
指数函数的综合问题
已知函数f(x)=2x+2ax+b,且f(1)=,f(2)=.
(1)求a,b的值;
(2)判断f(x)的奇偶性并证明;
(3)判断并证明函数f(x)在[0,+∞)上的单调性,并求f(x)的值域.
【思路探究】 (1)将两个已知条件代入解析式即可求a,b;(2)求出函数的定义域,再依据奇偶性的判断方法求解;(3)依据单调性的证明步骤给出过程,再依据单调性求值域.
【自主解答】 (1)∵∴根据题意得解得
故a,b的值分别为-1,0.
(2)由(1)知f(x)=2x+2-x,f(x)的定义域为R,关于原点对称.
因为f(-x)=2-x+2x=f(x),所以f(x)为偶函数.
(3)设任意x1因为x11,
所以f(x1)-f(x2)<0,即f(x1)当x=0时,函数取得最小值,为f(0)=1+1=2,
所以f(x)的值域为[2,+∞).
1.指数函数的单调性与底数有关,因此讨论指数函数的单调性时,一定要明确底数与1的大小关系.与指数函数有关的函数的单调性也往往与底数有关,其解决方法一般是利用函数单调性的定义.
2.指数函数本身不具有奇偶性,但是与指数函数有关的函数可以具有奇偶性,其解决方法一般是利用函数奇偶性的定义和性质.
设a为实数,f(x)=a-(x∈R).
(1)证明f(x)在R上为增函数;
(2)试确定a的值,使f(x)为奇函数.
【解】 (1)证明:设x1,x2∈R,x1f(x1)-f(x2)=(a-)-(a-)
=.
由于指数函数y=2x在R上为增函数,且x1所以2x1<2x2,即2x1-2x2<0.
又由2x>0,得2x1+1>0,2x2+1>0.
所以f(x1)-f(x2)<0,即f(x1)故f(x)在R上为增函数.
(2)若f(x)为奇函数,则f(-x)=-f(x),
即a-=-(a-).
变形得2a=+
=+==2.
解得a=1.所以当a=1时,f(x)为奇函数.
指数函数问题中的数形结合思想
(12分)关于x的方程|ax-1|+1-2a=0有两个相等的实数根,求实数a的取值范围.
【思路点拨】 将条件转化为直线y=2a与函数y=|ax-1|+1(a>0且a≠1)的图像有两个交点,利用数形结合法求解.
【规范解答】 当a>1时,函数y=|ax-1|+1通过平移变换和翻折变换可得如图所示的图像(实线),4分
由图可知1<2a<2,
即1矛盾.6分
当0由图可知1<2a<2,即∴当直线y=2a与函数y=|ax-1|+1的图像有两个交点时a的取值范围是{a|1.解答此题要注意底数的不确定性,因此作图时要注意分类讨论.
2.根据条件确定直线y=2a与函数图像的位置关系,然后由位置关系建立不等式,进而求得结果,其求解过程体现了数形结合思想在处理函数图像的交点时的应用.
1.能根据图像的平移、翻折、对称解决与指数函数相关的问题.
2.对于形如f(x)=ag(x)(a>0,且a≠1)的函数,可以利用复合函数的单调性,转化为指数函数y=ax及函数g(x)的单调性来处理,具体是:
当a>1时,函数f(x)的单调性与函数g(x)的单调性一致;
当03.在一些较复杂的函数问题中,基本函数的性质可以直接在解题过程中应用.同时注意将复杂函数问题转化为基本函数问题.
(见学生用书第45页)
1.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )
A.y=x3 B.y=|x|+1
C.y=-x2+1
D.y=2-|x|
【解析】 ∵y=x3在定义域R上是奇函数,∴A不对.
y=-x2+1在定义域R上是偶函数,但在(0,+∞)上是减函数,故C不对.
D中y=2-|x|=()|x|虽是偶函数,但在(0,+∞)上是减函数,只有B对.
【答案】 B
2.函数y=()1-x的单调增区间为( )
A.(-∞,+∞)
B.(0,+∞)
C.(1,+∞)
D.(0,1)
【解析】 设t=1-x,则y=()t,则函数t=1-x的递减区间为(-∞,+∞),即为y=()1-x的递增区间.
【答案】 A
3.函数y=ax-3+3(a>0且a≠1)的图像过定点________.
【解析】 法一 因为指数函数y=ax(a>0且a≠1)的图像过定点(0,1),所以在函数y=ax-3+3中,令x=3,得y=1+3=4,即函数的图像过定点(3,4).
法二 将原函数变形,得y-3=ax-3,然后把y-3看作是(x-3)的指数函数,所以当x-3=0时,y-3=1,即x=3,y=4,所以原函数的图像过定点(3,4).
【答案】 (3,4)
4.已知函数f(x)=+.
(1)求f(x)的定义域;
(2)讨论f(x)的奇偶性.
【解】 (1)由2x-1≠0,得2x≠1,即x≠0,
所以函数的定义域为(-∞,0)∪(0,+∞).
(2)因为函数f(x)的定义域关于坐标原点对称,
且f(-x)=+=+
=-+
=-++=-1+-
=-(+)=-f(x),
所以f(x)为奇函数.
(见学生用书第107页)
一、选择题
1.为了得到函数y=2x-3+1的图像,只需把函数y=2x上的所有点( )
A.向右平移3个单位长度,再向下平移1个单位长度
B.向左平移3个单位长度,再向下平移1个单位长度
C.向右平移3个单位长度,再向上平移1个单位长度
D.向左平移3个单位长度,再向上平移1个单位长度
【解析】 y=2xy=2x-3y=2x-3+1.
【答案】 C
2.函数y=()|x|的值域为( )
A.{y|y>0} B.{y|y≤1}
C.{y|y≥1}
D.{y|0【解析】 由于|x|≥0,且y=()|x|为偶函数,结合其图像知0【答案】 D
3.若函数y=ax+b-1(a>0且a≠1)的图像经过第二、三、四象限,则一定有( )
A.00
B.a>1,且b>0
C.0D.a<1,且b>0
【解析】 根据题意,画出函数y=ax+b-1(a>0且a≠1)的大致图像,如图所示.所以0【答案】 C
4.若不等式2-x+a+1>0对一切x∈R恒成立,则实数a的取值范围是( )
A.a<-1
B.a≤-1
C.a>-1
D.a≥-1
【解析】 原不等式可化为()x>-a-1,由于()x>0,
所以要使原不等式对x∈R恒成立,只需-a-1≤0,
即a≥-1.
【答案】 D
5.(2013·商丘高一检测)若函数f(x)=
是R上的增函数,则实数a的取值范围为( )
A.(1,+∞)
B.(1,8)
C.(4,8)
D.[4,8)
【解析】 因为f(x)在R上是增函数,故结合图像(图略)知解得4≤a<8.
【答案】 D
二、填空题
6.若f(x)=π-(x-u)2的最大值为m,且f(x)是偶函数,则m+n=________.
【解析】 因为f(-x)=f(x),
所以π-(x+u)2=π-(x-u)2
所以(x+u)2=(x-u)2.
所以u=0,f(x)=π-x2,
因为x2≥0,所以-x2≤0.
所以0<π-x2≤1.
所以m=1,故m+n=1.
7.若函数f(x)=则不等式f(x)≥的解集为________.
【解析】 (1)当x≥0时,由f(x)≥得()x≥,
∴0≤x≤1.
(2)当x<0时,不等式≥明显不成立.
综上可知不等式f(x)≥的解集是{x|0≤x≤1}.
【答案】 {x|0≤x≤1}
8.(2013·大连高一检测)若关于x的方程()|x|+m=0有实数解,则实数m的取值范围是________.
【解析】 法一 ∵0<()|x|≤1,
∴m<()|x|+m≤m+1.
要使方程()|x|+m=0有解,只要m<0≤m+1,
解得-1≤m<0,故实数m的取值范围是[-1,0).
法二 令y=()|x|+m,作函数图像,如图:
依题意,函数y=()|x|+m的图像与x轴有交点,
∴解得-1≤m<0,即m∈[-1,0).
【答案】 [-1,0)
三、解答题
9.画出函数y=2|x+1|的图像,并根据图像指出它的单调区间.
【解】 变换作图,y=2xy=2|x|y=2|x+1|,如图.
由图可知函数y=2|x+1|在(-∞,-1)]上单调递减,
在(-1,+∞)上单调递增.
10.求函数y=()x2-2x+2(0≤x≤3)的值域.
【解】 令t=x2-2x+2,则y=()t,
又t=x2-2x+2=(x-1)2+1,0≤x≤3,
∴当x=1时,tmin=1;当x=3时,tmax=5.
故1≤t≤5,∴()5≤y≤()1,
故所求函数的值域为[,].
11.已知定义域为R的函数f(x)=是奇函数.
(1)求a,b的值;
(2)若对于任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
【解】 (1)∵f(x)为奇函数且在x=0处有意义,
∴f(0)=0,即=0,
∴b=1,
∴f(x)=.
又∵f(-1)=-f(1),
∴=-,
∴a=2.
(2)由(1)知f(x)=,
先研究f(x)=的单调性.
∵f(x)==-+,
∴f(x)=在R上为减函数.
∵f(x)为奇函数,
∴f(t2-2t)+f(2t2-k)<0,
即f(t2-2t)<-f(2t2-k)
=f(-2t2+k).
又∵f(x)在R为减函数,
∴t2-2t>-2t2+k,
即对一切t∈R,有3t2-2t-k>0,
∴Δ<0,即4+12k<0,
∴k<-.
故k的取值范围是(-∞,).
指数函数的图像与性质的应用
学案
课标解读
1.理解并掌握指数函数的图像和性质.(重点)2.掌握函数图像的简单变换.(易混点)3.能运用指数函数的有关性质去研究指数型函数的性质.(难点)
知识
函数图像的变换
【问题导思】
若已知函数f(x)=2x的图像.
1.如何得到f(x)=2x-1的图像?
【提示】 向右平移1个单位.
2.如何得到f(x)=2x-2的图像?
【提示】 向下平移2个单位.
3.如何得到f(x)=()x的图像?
【提示】 作f(x)=2x关于y轴的对称图像.
4.如何得到f(x)=-2x的图像?
【提示】 将f(x)=2x的图像以x轴为对称轴翻折到x轴下方.
1.平移变换
(1)左右平移:y=f(x)y=f(x+a)
特征:左加右减:
(2)上下平移:y=f(x)y=f(x)+k
特征:上加下减.
2.对称变换
(1)y=f(x)y=-f(x);
(2)y=f(x)y=f(-x);
(3)y=f(x)y=-f(-x).
3.翻折变换
(1)y=f(x)
y=f(|x|).
(2)y=f(x)
Y=|f(x)|
(见学生用书第43页)
类型1
函数图像的作法
利用函数f(x)=()x的图像,作出下列函数的图像:
(1)f(x+1);(2)-f(x);(3)f(-x).
【思路探究】 作出y=()x
的图像→明确f(x)与f(x+1),
-f(x),f(-x)图像间
的关系
分别得出图像
【自主解答】 作出f(x)=()x的图像,如图所示:
(1)f(x+1)的图像:需将f(x)的图像向左平移1个单位得f(x+1)的图像,如图(1).
(2)-f(x)的图像:作f(x)的图像关于x轴对称的图像得-f(x)的图像,如图(2).
(3)f(-x)的图像:作f(x)的图像关于y轴对称的图像得f(-x)的图像,如图(3).
1.利用已知的函数图像作图,主要运用图像的平移、对称等变换,平移变换需分清楚向何方向移,要移多少个单位,如(1);对称变换需分清对称轴是什么,如(2)(3).
2.利用变换作图,一般步骤是:
选基函数→写出变换过程→画图像
函数y=2|x|的图像是( )
【解析】 法一 由于y=2|x|=所以A正确.
法二 y=2|x|对称变换
y=2|x|,知选A.
【答案】 A
类型2
与指数函数有关的复合函数
求下列函数的单调区间:
(1)y=3x2-2x+7;(2)y=4x-2·2x+5.
【思路探究】 将复合函数写成y=f(u),u=φ(x)的形式,然后利用复合函数的单调性求解.
【自主解答】 (1)函数的定义域为R,对u=x2-2x+7=(x-1)2+6,当x≥1时,u为增函数,x≤1时,u为减函数,又3>1,
∴函数y=3x2-2x+7的增区间为[1,+∞),减区间为(-∞,1].
(2)令2x=t,则t是x的增函数,
y=t2-2t+5=(t-1)2+4,
当t≥1,即2x≥1,即x≥0时,y是t的增函数;
当t≤1,即2x≤1,即x≤0时,y是t的减函数;
又函数的定义域为R,
∴函数y=4x-2·2x+5的单调增区间是[0,+∞),减区间是(-∞,0].
1.求函数的单调区间,首先求函数的定义域,对复合函数的单调性,应注意y=f(u)与u=g(x)单调性的一致性和相反性.
2.在复合函数中,一般情况下,如果两个函数都是增函数或都是减函数,则复合函数是增函数;如果两个函数一增一减,则复合函数为减函数,简称“同增异减”.
(1)(2013·荆州检测)函数y=()x2-3x+2的单调增区间是________.
(2)y=(-1)-x2+2x+3的单调增区间是( )
A.(1,+∞) B.(-∞,1]
C.(1,3)
D.(-1,1)
【解析】 令u=x2-3x+2=(x-)2-,令y=()u在定义域内是减函数,而求y=()x2-3x+2的增区间,只需求u的减区间,∴x∈(-∞,].
(2)函数y的定义域为R,u=-x2+2x+3=-(x-1)2+4;x≥1时,u是减函数,又0<-1<1,
∴y的增区间为(1,+∞).
【答案】 (1)(-∞,] (2)A
类型3
指数函数的综合问题
已知函数f(x)=2x+2ax+b,且f(1)=,f(2)=.
(1)求a,b的值;
(2)判断f(x)的奇偶性并证明;
(3)判断并证明函数f(x)在[0,+∞)上的单调性,并求f(x)的值域.
【思路探究】 (1)将两个已知条件代入解析式即可求a,b;(2)求出函数的定义域,再依据奇偶性的判断方法求解;(3)依据单调性的证明步骤给出过程,再依据单调性求值域.
【自主解答】 (1)∵∴根据题意得解得
故a,b的值分别为-1,0.
(2)由(1)知f(x)=2x+2-x,f(x)的定义域为R,关于原点对称.
因为f(-x)=2-x+2x=f(x),所以f(x)为偶函数.
(3)设任意x1
所以f(x1)-f(x2)<0,即f(x1)
所以f(x)的值域为[2,+∞).
1.指数函数的单调性与底数有关,因此讨论指数函数的单调性时,一定要明确底数与1的大小关系.与指数函数有关的函数的单调性也往往与底数有关,其解决方法一般是利用函数单调性的定义.
2.指数函数本身不具有奇偶性,但是与指数函数有关的函数可以具有奇偶性,其解决方法一般是利用函数奇偶性的定义和性质.
设a为实数,f(x)=a-(x∈R).
(1)证明f(x)在R上为增函数;
(2)试确定a的值,使f(x)为奇函数.
【解】 (1)证明:设x1,x2∈R,x1
=.
由于指数函数y=2x在R上为增函数,且x1
又由2x>0,得2x1+1>0,2x2+1>0.
所以f(x1)-f(x2)<0,即f(x1)
(2)若f(x)为奇函数,则f(-x)=-f(x),
即a-=-(a-).
变形得2a=+
=+==2.
解得a=1.所以当a=1时,f(x)为奇函数.
指数函数问题中的数形结合思想
(12分)关于x的方程|ax-1|+1-2a=0有两个相等的实数根,求实数a的取值范围.
【思路点拨】 将条件转化为直线y=2a与函数y=|ax-1|+1(a>0且a≠1)的图像有两个交点,利用数形结合法求解.
【规范解答】 当a>1时,函数y=|ax-1|+1通过平移变换和翻折变换可得如图所示的图像(实线),4分
由图可知1<2a<2,
即
当0
2.根据条件确定直线y=2a与函数图像的位置关系,然后由位置关系建立不等式,进而求得结果,其求解过程体现了数形结合思想在处理函数图像的交点时的应用.
1.能根据图像的平移、翻折、对称解决与指数函数相关的问题.
2.对于形如f(x)=ag(x)(a>0,且a≠1)的函数,可以利用复合函数的单调性,转化为指数函数y=ax及函数g(x)的单调性来处理,具体是:
当a>1时,函数f(x)的单调性与函数g(x)的单调性一致;
当0
(见学生用书第45页)
1.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )
A.y=x3 B.y=|x|+1
C.y=-x2+1
D.y=2-|x|
【解析】 ∵y=x3在定义域R上是奇函数,∴A不对.
y=-x2+1在定义域R上是偶函数,但在(0,+∞)上是减函数,故C不对.
D中y=2-|x|=()|x|虽是偶函数,但在(0,+∞)上是减函数,只有B对.
【答案】 B
2.函数y=()1-x的单调增区间为( )
A.(-∞,+∞)
B.(0,+∞)
C.(1,+∞)
D.(0,1)
【解析】 设t=1-x,则y=()t,则函数t=1-x的递减区间为(-∞,+∞),即为y=()1-x的递增区间.
【答案】 A
3.函数y=ax-3+3(a>0且a≠1)的图像过定点________.
【解析】 法一 因为指数函数y=ax(a>0且a≠1)的图像过定点(0,1),所以在函数y=ax-3+3中,令x=3,得y=1+3=4,即函数的图像过定点(3,4).
法二 将原函数变形,得y-3=ax-3,然后把y-3看作是(x-3)的指数函数,所以当x-3=0时,y-3=1,即x=3,y=4,所以原函数的图像过定点(3,4).
【答案】 (3,4)
4.已知函数f(x)=+.
(1)求f(x)的定义域;
(2)讨论f(x)的奇偶性.
【解】 (1)由2x-1≠0,得2x≠1,即x≠0,
所以函数的定义域为(-∞,0)∪(0,+∞).
(2)因为函数f(x)的定义域关于坐标原点对称,
且f(-x)=+=+
=-+
=-++=-1+-
=-(+)=-f(x),
所以f(x)为奇函数.
(见学生用书第107页)
一、选择题
1.为了得到函数y=2x-3+1的图像,只需把函数y=2x上的所有点( )
A.向右平移3个单位长度,再向下平移1个单位长度
B.向左平移3个单位长度,再向下平移1个单位长度
C.向右平移3个单位长度,再向上平移1个单位长度
D.向左平移3个单位长度,再向上平移1个单位长度
【解析】 y=2xy=2x-3y=2x-3+1.
【答案】 C
2.函数y=()|x|的值域为( )
A.{y|y>0} B.{y|y≤1}
C.{y|y≥1}
D.{y|0
3.若函数y=ax+b-1(a>0且a≠1)的图像经过第二、三、四象限,则一定有( )
A.0
B.a>1,且b>0
C.0
【解析】 根据题意,画出函数y=ax+b-1(a>0且a≠1)的大致图像,如图所示.所以0
4.若不等式2-x+a+1>0对一切x∈R恒成立,则实数a的取值范围是( )
A.a<-1
B.a≤-1
C.a>-1
D.a≥-1
【解析】 原不等式可化为()x>-a-1,由于()x>0,
所以要使原不等式对x∈R恒成立,只需-a-1≤0,
即a≥-1.
【答案】 D
5.(2013·商丘高一检测)若函数f(x)=
是R上的增函数,则实数a的取值范围为( )
A.(1,+∞)
B.(1,8)
C.(4,8)
D.[4,8)
【解析】 因为f(x)在R上是增函数,故结合图像(图略)知解得4≤a<8.
【答案】 D
二、填空题
6.若f(x)=π-(x-u)2的最大值为m,且f(x)是偶函数,则m+n=________.
【解析】 因为f(-x)=f(x),
所以π-(x+u)2=π-(x-u)2
所以(x+u)2=(x-u)2.
所以u=0,f(x)=π-x2,
因为x2≥0,所以-x2≤0.
所以0<π-x2≤1.
所以m=1,故m+n=1.
7.若函数f(x)=则不等式f(x)≥的解集为________.
【解析】 (1)当x≥0时,由f(x)≥得()x≥,
∴0≤x≤1.
(2)当x<0时,不等式≥明显不成立.
综上可知不等式f(x)≥的解集是{x|0≤x≤1}.
【答案】 {x|0≤x≤1}
8.(2013·大连高一检测)若关于x的方程()|x|+m=0有实数解,则实数m的取值范围是________.
【解析】 法一 ∵0<()|x|≤1,
∴m<()|x|+m≤m+1.
要使方程()|x|+m=0有解,只要m<0≤m+1,
解得-1≤m<0,故实数m的取值范围是[-1,0).
法二 令y=()|x|+m,作函数图像,如图:
依题意,函数y=()|x|+m的图像与x轴有交点,
∴解得-1≤m<0,即m∈[-1,0).
【答案】 [-1,0)
三、解答题
9.画出函数y=2|x+1|的图像,并根据图像指出它的单调区间.
【解】 变换作图,y=2xy=2|x|y=2|x+1|,如图.
由图可知函数y=2|x+1|在(-∞,-1)]上单调递减,
在(-1,+∞)上单调递增.
10.求函数y=()x2-2x+2(0≤x≤3)的值域.
【解】 令t=x2-2x+2,则y=()t,
又t=x2-2x+2=(x-1)2+1,0≤x≤3,
∴当x=1时,tmin=1;当x=3时,tmax=5.
故1≤t≤5,∴()5≤y≤()1,
故所求函数的值域为[,].
11.已知定义域为R的函数f(x)=是奇函数.
(1)求a,b的值;
(2)若对于任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
【解】 (1)∵f(x)为奇函数且在x=0处有意义,
∴f(0)=0,即=0,
∴b=1,
∴f(x)=.
又∵f(-1)=-f(1),
∴=-,
∴a=2.
(2)由(1)知f(x)=,
先研究f(x)=的单调性.
∵f(x)==-+,
∴f(x)=在R上为减函数.
∵f(x)为奇函数,
∴f(t2-2t)+f(2t2-k)<0,
即f(t2-2t)<-f(2t2-k)
=f(-2t2+k).
又∵f(x)在R为减函数,
∴t2-2t>-2t2+k,
即对一切t∈R,有3t2-2t-k>0,
∴Δ<0,即4+12k<0,
∴k<-.
故k的取值范围是(-∞,).
