3.3.3 指数函数及其性质(一)学案1(含答案)
文档属性
| 名称 | 3.3.3 指数函数及其性质(一)学案1(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 60.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-15 22:19:29 | ||
图片预览


文档简介
3.3.3指数函数及其性质(一)学案
主要考点梳理
1.指数幂的有关概念
(1)正整数指数幂;
(2)零指数幂;
(3)负整数指数幂;
(4)正分数指数幂;
(5)负分数指数幂;
(6)的正分数指数幂等于.的负分数指数幂没有意义.
2.有理指数幂的运算性质
说明:上述有理指数幂的运算性质,对于无理数指数幂也适用.
3.指数函数的定义
形如的函数叫做指数函数.
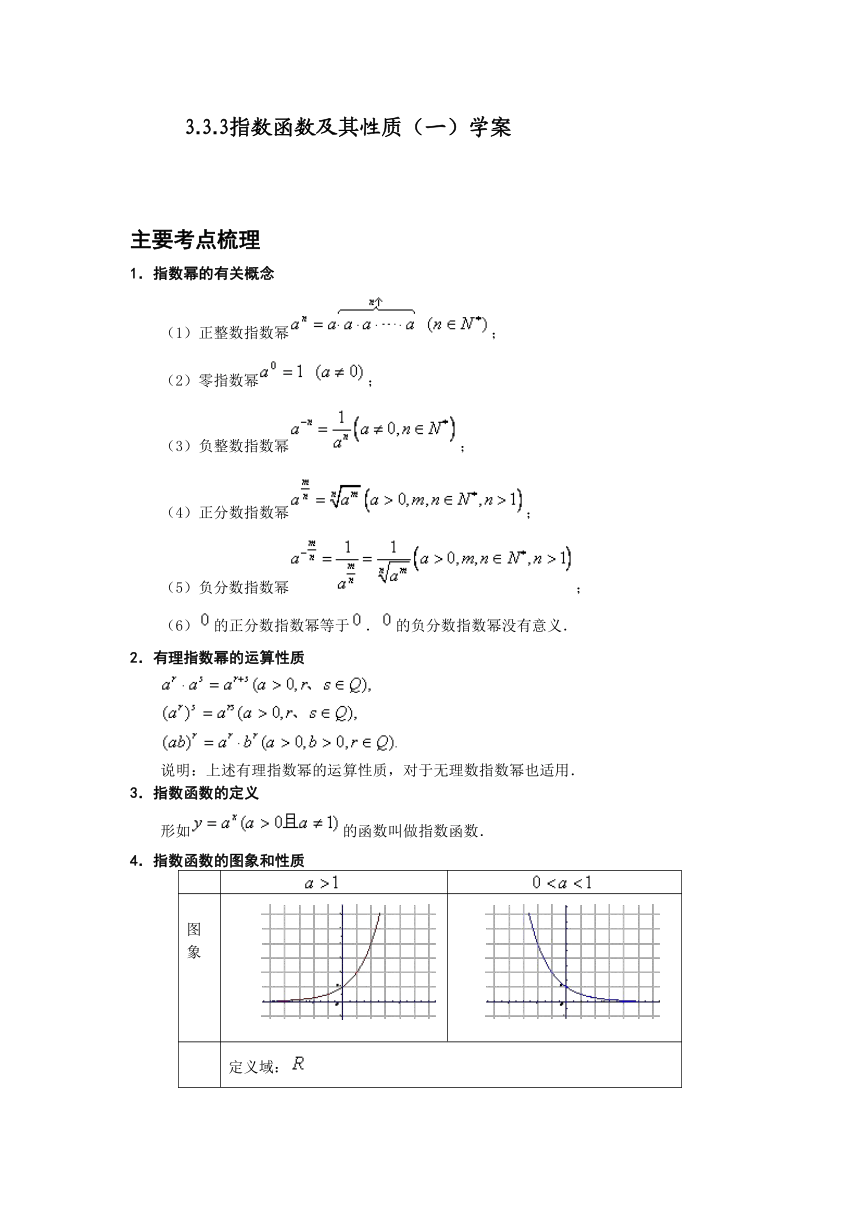
4.指数函数的图象和性质
图象
性质
定义域:
值域:
过点,即时,
当时,;当时,.
当时,;当时,.
在
上是增函数
在上是减函数
金题精讲
题一
题面:计算:(1);
(2);
(3).
题二
题面:已知.求下列各式的值:
(1); (2).
题三
题面:设函数若,则的取值范围是____________.
题四
题面:比较下列各题中两个值的大小:
(1)与; (2)与;
(3)与;
(4)与.
题五
题面:函数的图象大致为
(
).
题六
题面:已知函数若有则的取值范围为(
).
(A)
(B)
(C)
(D)
课后拓展练习
注:此部分为老师根据本讲课程内容为大家精选的课下拓展题目,故不在课堂中讲解,请同学们课下自己练习并对照详解进行自测.
题一
题面:计算下列各式(式中字母都是正数)
(); ().
题二
题面:设为定义在上的奇函数,当时,(为常数),则(
).
(A)
(B)
(C)1
(D)3
题三
题面:设,求证.
讲义参考答案
金题精讲
题一
答案:()原式;()原式;()原式.
题二
答案:(1);(2).
题三
答案:的取值范围是.
题四
答案:(1);(2);(3);(4).
题五
答案:A.
题六
答案:B.
课后拓展练习
题一
答案:(1);(2).
详解:(1)原式;
(2)原式.
题二
答案:A.
详解:由,,所以.
故,所以,选A.
题三
答案:见详解.
证明:.
主要考点梳理
1.指数幂的有关概念
(1)正整数指数幂;
(2)零指数幂;
(3)负整数指数幂;
(4)正分数指数幂;
(5)负分数指数幂;
(6)的正分数指数幂等于.的负分数指数幂没有意义.
2.有理指数幂的运算性质
说明:上述有理指数幂的运算性质,对于无理数指数幂也适用.
3.指数函数的定义
形如的函数叫做指数函数.
4.指数函数的图象和性质
图象
性质
定义域:
值域:
过点,即时,
当时,;当时,.
当时,;当时,.
在
上是增函数
在上是减函数
金题精讲
题一
题面:计算:(1);
(2);
(3).
题二
题面:已知.求下列各式的值:
(1); (2).
题三
题面:设函数若,则的取值范围是____________.
题四
题面:比较下列各题中两个值的大小:
(1)与; (2)与;
(3)与;
(4)与.
题五
题面:函数的图象大致为
(
).
题六
题面:已知函数若有则的取值范围为(
).
(A)
(B)
(C)
(D)
课后拓展练习
注:此部分为老师根据本讲课程内容为大家精选的课下拓展题目,故不在课堂中讲解,请同学们课下自己练习并对照详解进行自测.
题一
题面:计算下列各式(式中字母都是正数)
(); ().
题二
题面:设为定义在上的奇函数,当时,(为常数),则(
).
(A)
(B)
(C)1
(D)3
题三
题面:设,求证.
讲义参考答案
金题精讲
题一
答案:()原式;()原式;()原式.
题二
答案:(1);(2).
题三
答案:的取值范围是.
题四
答案:(1);(2);(3);(4).
题五
答案:A.
题六
答案:B.
课后拓展练习
题一
答案:(1);(2).
详解:(1)原式;
(2)原式.
题二
答案:A.
详解:由,,所以.
故,所以,选A.
题三
答案:见详解.
证明:.
