3.5 对数函数 教案2

3.5
对数函数
教案
【教学目标】
1、使学生理解对数函数的定义，进一步掌握对数函数的图像和性质。
2、：通过定义的复习，图像特征的观察、巩固过程使学生懂得理论与实践
的辩证关系，适时渗透分类讨论的数学思想，培养学生的探索发现能力和分析问题、解决问题的能力。
3、通过学生的参与过程，培养他们手脑并用、多思勤练的良好学习习惯和勇于探索、锲而不舍的治学精神。
【教学重难点】
教学重点：对数函数的图像和性质

教学难点：底数 a 的变化对函数性质的影响
【教学过程】
（一）预习检查、总结疑惑
检查落实了学生的预习情况并了解了学生的疑惑，使教学具有了针对性.
（二）情景导入、展示目标
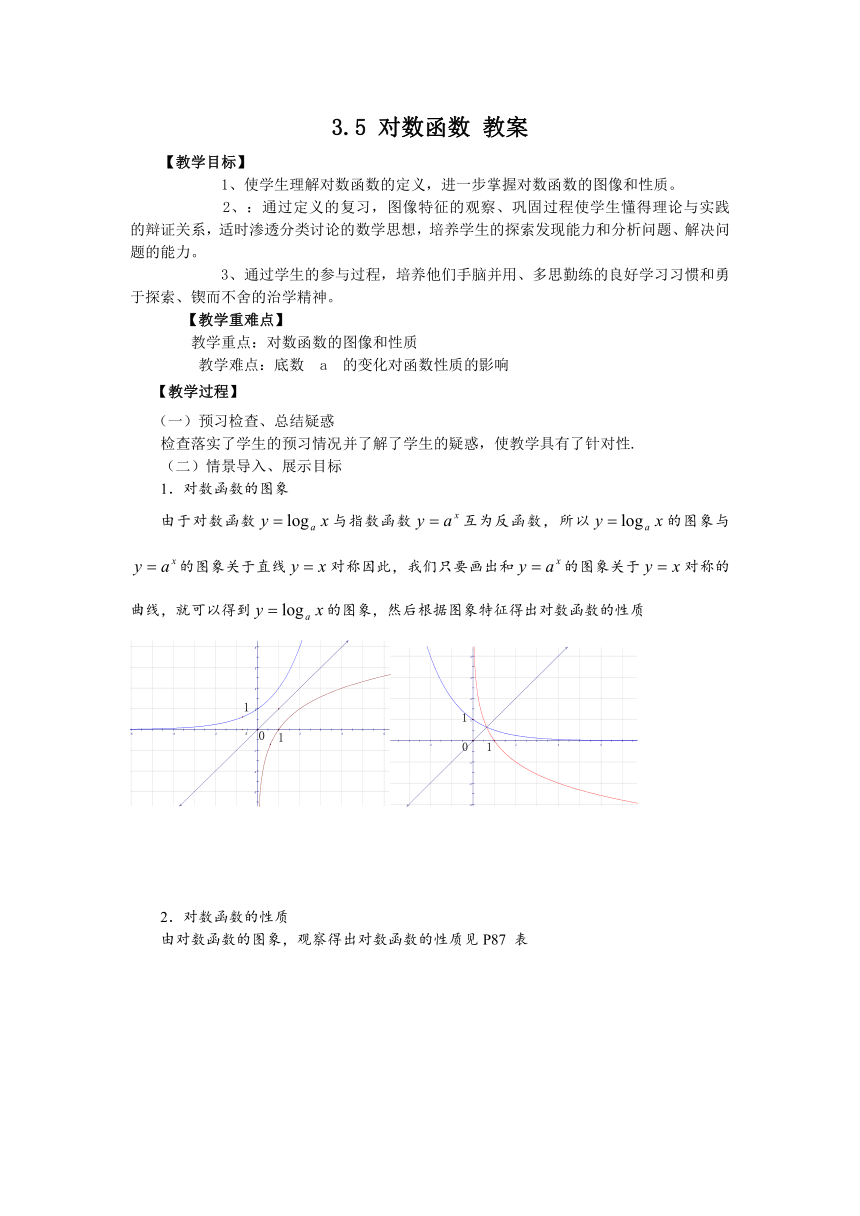
1．对数函数的图象
由于对数函数与指数函数互为反函数，所以的图象与的图象关于直线对称因此，我们只要画出和的图象关于对称的曲线，就可以得到的图象，然后根据图象特征得出对数函数的性质
2．对数函数的性质
由对数函数的图象，观察得出对数函数的性质见P87
表
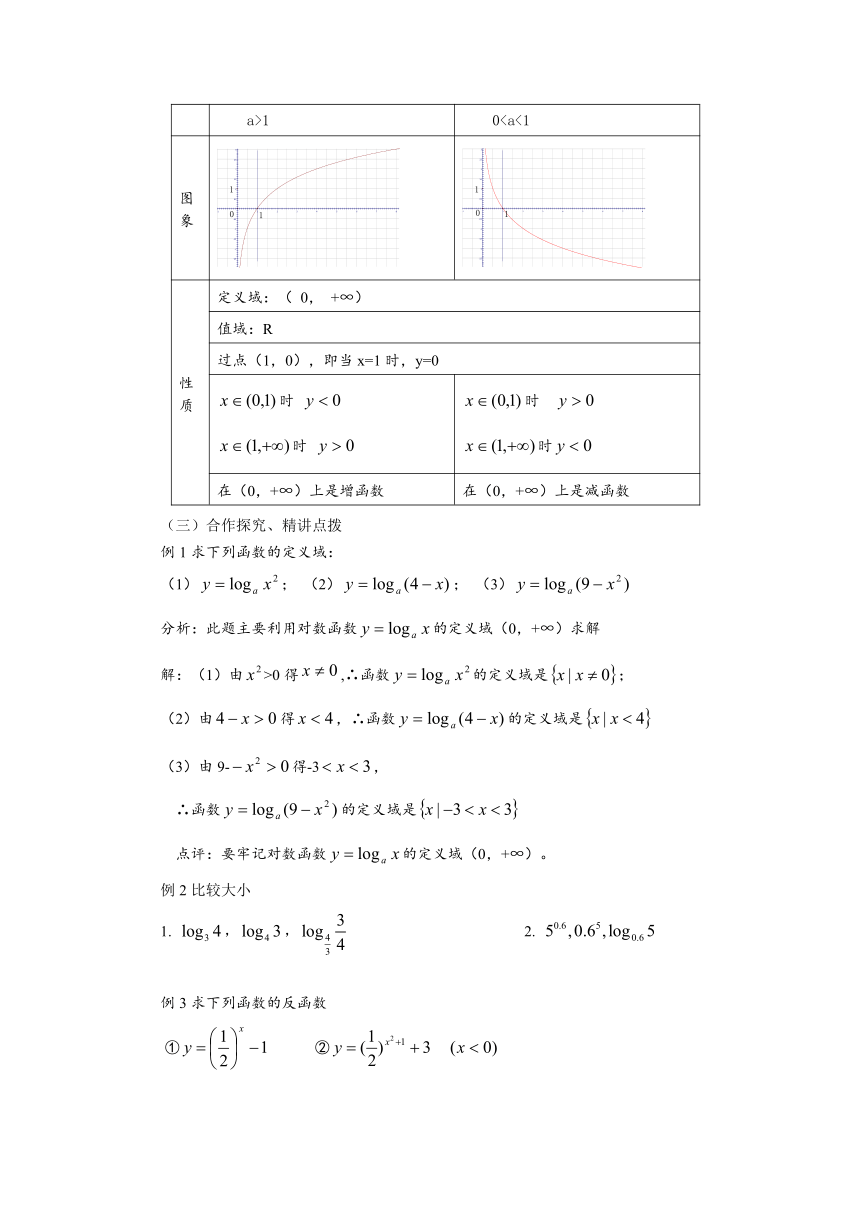
a>1
0图象
性质
定义域：（
0，
+∞）
值域：R
过点（1，0），即当x=1时，y=0
时
时
时
时
在（0，+∞）上是增函数
在（0，+∞）上是减函数
（三）合作探究、精讲点拨
例1求下列函数的定义域：
（1）；
（2）；
（3）
分析：此题主要利用对数函数的定义域（0，+∞）求解
解：（1）由>0得,∴函数的定义域是；
（2）由得，∴函数的定义域是
（3）由9-得-3，
∴函数的定义域是
点评：要牢记对数函数的定义域（0，+∞）。
例2比较大小
1.
，，
2.
例3求下列函数的反函数
①
②
解：①
∴
②
∴
例4
画出函数y=x及y=的图象，并且说明这两个函数的相同性质和不同性质.
解：相同性质：两图象都位于y轴右方，都经过点（1，0），这说明两函数的定义域都是（0，+∞），且当x=1,y=0.
不同性质：y=x的图象是上升的曲线，y=的图象是下降的曲线，这说明前者在（0，+∞）上是增函数，后者在（0，+∞）上是减函数.
（四）反思总结、当堂检测
1.求下列函数的定义域：
（1）y=(1-x)
(2)y=
(3)
y=
解：（1）由1-x＞0得x＜1
∴所求函数定义域为{x|x＜1
(2)由x≠0，得x≠1，又x＞0
∴所求函数定义域为{x|x＞0且x≠1}
(3)由
∴所求函数定义域为{x|x＜
(4)由
∴x≥1
∴所求函数定义域为{x|x≥1}
2.函数恒过的定点坐标是
（
）
A.
B.
C.
D.
3.若求实数的取值范围
【板书设计】
一、对数函数性质
1.
图像
2.
性质
二、例题
例1
变式1
例2
变式2
【作业布置】导学案课后练习与提高