3.5.2 对数函数y=log2x的图像和性质 同步测试1(含答案)
文档属性
| 名称 | 3.5.2 对数函数y=log2x的图像和性质 同步测试1(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 151.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-14 00:00:00 | ||
图片预览




文档简介
3.5.2
对数函数y=log2x的图像和性质
同步测试
(30分钟 50分)
一、选择题(每小题3分,共18分)
1.函数y=lox的反函数是( )
A.y=-()x B.y=()x
C.y=3x
D.y=-3x
【解析】选B.对数函数y=logax的反函数是指数函数y=ax,故函数y=lox的反函数是y=.
【变式训练】函数y=ex的图像与函数y=f(x)的图像关于直线y=x对称,则( )
A.f(x)=lgx
B.f(x)=log2x
C.f(x)=lnx
D.f(x)=xe
【解析】选C.易知y=f(x)是y=ex的反函数,
所以f(x)=lnx.故选C.
2.(2014·郑州高一检测)已知函数f(x)=log2(x+1),若f(α)=1,则α=( )
A.0
B.1
C.2
D.3
【解析】选B.因为f(α)=log2(α+1)=1,所以α+1=2.所以α=1.
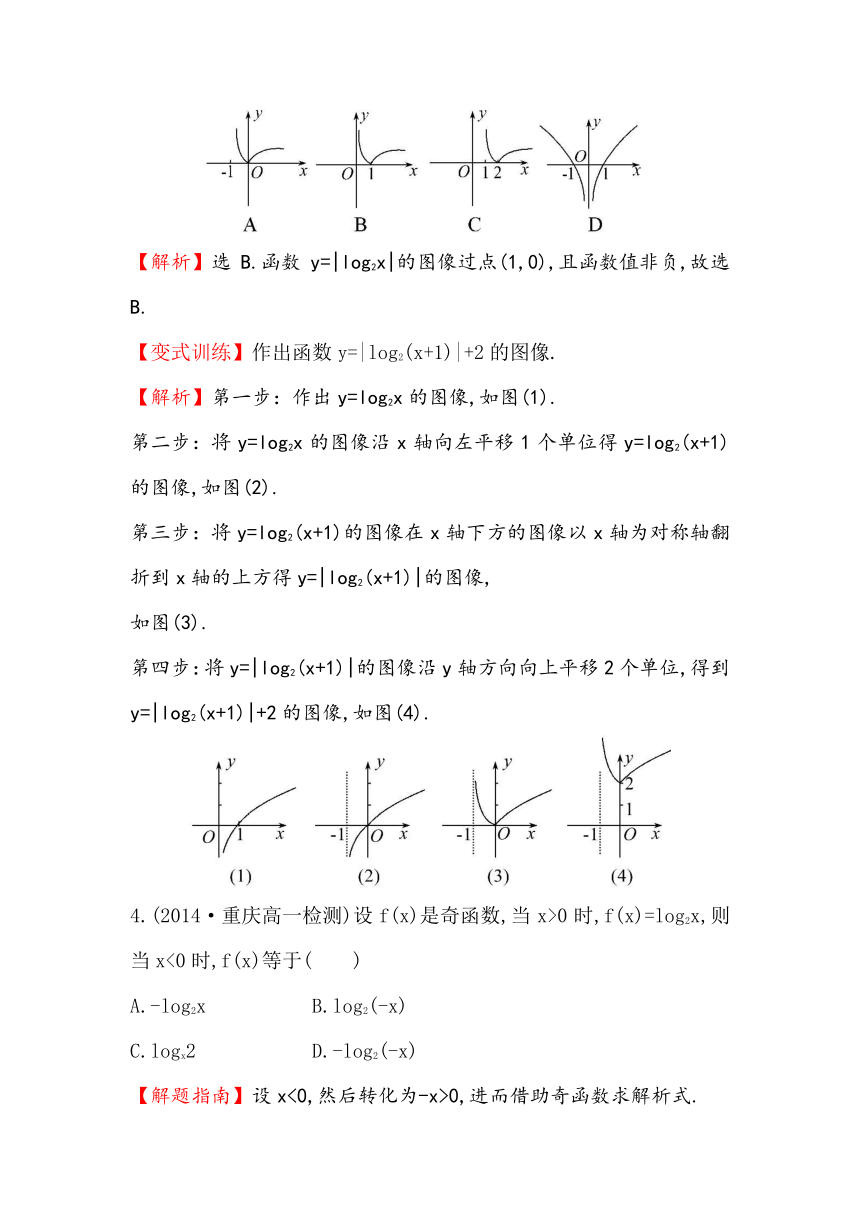
3.(2014·温州高一检测)函数y=|log2x|的图像是( )
【解析】选B.函数y=|log2x|的图像过点(1,0),且函数值非负,故选B.
【变式训练】作出函数y=|log2(x+1)|+2的图像.
【解析】第一步:作出y=log2x的图像,如图(1).
第二步:将y=log2x的图像沿x轴向左平移1个单位得y=log2(x+1)的图像,如图(2).
第三步:将y=log2(x+1)的图像在x轴下方的图像以x轴为对称轴翻折到x轴的上方得y=|log2(x+1)|的图像,
如图(3).
第四步:将y=|log2(x+1)|的图像沿y轴方向向上平移2个单位,得到y=|log2(x+1)|+2的图像,如图(4).
4.(2014·重庆高一检测)设f(x)是奇函数,当x>0时,f(x)=log2x,则当x<0时,f(x)等于( )
A.-log2x
B.log2(-x)
C.logx2
D.-log2(-x)
【解题指南】设x<0,然后转化为-x>0,进而借助奇函数求解析式.
【解析】选D.因为x<0,所以-x>0,
所以f(-x)=log2(-x).
又因为f(x)是奇函数,所以f(-x)=-f(x).
所以f(x)=-log2(-x).故选D.
【误区警示】本题在求解过程中常因搞混“x与-x”的转化关系,导致求解错误.
5.(2014·赣州高一检测)函数f(x)=的图像与函数g(x)=log2x图像交点个数是( )
A.1
B.2
C.3
D.4
【解析】选C.函数f(x)与g(x)在同一坐标系内的图像如图所示.
由图像可知,两图像有三个交点.
6.(2014·台州高一检测)已知函数f(x)=|log2x|,正实数m,n且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m,n的值分别为( )
A.,2
B.,
C.,2
D.,4
【解析】选A.如图所示.
由f(m)=f(n)可知,m,n位于1的两侧,
又f(x)在区间[m2,n]上的最大值为2,
所以|log2m2|=2,
所以log2m2=-2,
所以m=.
又f==1,
所以f(n)=log2n=1,所以n=2.
所以m=,n=2.
二、填空题(每小题4分,共12分)
7.(2014·德化高一检测)对数函数f(x)满足f(9)=2,则f(3)= .
【解析】设对数函数为f(x)=logax,所以2=loga9,
所以a=3,所以解析式为y=log3x.
所以f(3)=log33=1.
答案:1
8.已知f(x)=log2x,则f+f= .
【解析】f+f=log2+log2
=log2=-2.
答案:-2
9.(2014·浏阳高一检测)函数f(x)=的定义域为 .
【解题指南】分母不为零,真数大于零,同时成立.
【解析】由解得x<4且x≠3,
所以定义域为{x|x<4且x≠3}.
答案:{x|x<4且x≠3}
【变式训练】(2014·广州高一检测)函数f(x)=+lg(1+x)的定义域是( )
A.(-∞,-1)
B.(1,+∞)
C.(-1,1)∪(1,+∞)
D.(-∞,+∞)
【解析】选C.要使函数有意义,则有
即
所以函数的定义域为(-1,1)∪(1,+∞).
三、解答题(每小题10分,共20分)
10.函数f(x)=(a2-a+1)log(a+1)x是对数函数,求实数a的值.
【解析】因为函数f(x)=(a2-a+1)log(a+1)x是对数函数,
所以a2-a+1=1,解得a=0或a=1.
又a+1>0,a+1≠1,所以a=1.
【误区警示】本题在求解过程中常常因为忘记检验“a+1>0,a+1≠1”而产生增解a=0.
11.利用函数f(x)=log2x的图像和性质解决以下问题:
(1)比较log2与log2的大小.
(2)若log2(2-x)>0,求x的取值范围.
【解析】(1)函数f(x)=log2x在(0,+∞)上为增函数,
又因为>,所以log2>log2.
(2)log2(2-x)>0,即log2(2-x)>log21,
因为函数y=log2x为增函数,
所以2-x>1,所以x<1.
所以x的取值范围为(-∞,1).
(30分钟 50分)
一、选择题(每小题4分,共16分)
1.已知全集U=R,集合A为函数f(x)=ln(x-1)的定义域,则A=( )
A.(-∞,1]
B.[1,+∞)
C.(-∞,2]
D.[2,+∞)
【解析】选A.函数f(x)=ln(x-1)的定义域为{x|x>1},
所以 UA={x|x≤1}.
2.设f(log2x)=2x(x>0),则f(3)=( )
A.128
B.256
C.512
D.8
【解析】选B.令log2x=3,则x=8,所以f(3)=28=256.
【一题多解】令log2x=t,则x=2t,
所以f(t)=,所以f(3)=28=256.
3.(2014·合肥高一检测)若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,其图像经过点(,a),则f(x)=( )
A.log2x
B.lox
C.
D.x2
【解题指南】先求反函数,再借助对数函数的运算性质求a的值,最后求f(x)的解析式.
【解析】选B.因为函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,所以f(x)=logax.
因为f(x)=logax的图像经过点(,a),
所以loga=a a=,即f(x)=lox.
4.(2014·赤峰高一检测)已知f(x)是函数y=log2x的反函数,则y=f(1-x)的图像是( )
【解析】选C.函数y=log2x的反函数为y=2x,故f(x)=2x,于是f(1-x)=21-x=()x-1,此函数在R上为减函数,其图像过点(0,2),所以选项C中的图像符合要求.
二、填空题(每小题5分,共10分)
5.(2014·赣州高一检测)已知函数f(x)=log2(x+1)的值域是[1,2],那么函数f(x)的定义域是 .
【解析】因为f(x)=log2(x+1)的值域为[1,2],
所以1≤log2(x+1)≤2,
所以2≤x+1≤4,即1≤x≤3,
所以f(x)的定义域为[1,3].
答案:[1,3]
【变式训练】若f(x)=则满足f(x)=的x的值为 .
【解题指南】在不同的对应关系下求解x的值,最后求其并集便可.
【解析】因为当x≤1时,f(x)=≥,
所以满足f(x)=的x∈(1,+∞),
即log81x=,所以x==3.
答案:3
6.(2014·天津高一检测)函数f(x)=log2x在区间[a,2a](a>0)上的最大值与最小值之差为 .
【解析】因为f(x)=log2x在区间[a,2a]上是增函数,
所以f(x)max-f(x)min=f(2a)-f(a)=log22a-log2a=log22=1.
答案:1
三、解答题(每小题12分,共24分)
7.(2014·长沙高一检测)已知函数f(x)=的定义域为A,函数g(x)=(-1≤x≤0)的值域为B.
(1)求A∩B.
(2)若C={y|y≤a-1},且B C,求a的取值范围.
【解题指南】由题意列出不等式组,再解不等式组,得出函数的定义域A.再借助指数函数的单调性求集合B.最后借助集合的关系求解(1)(2).
【解析】(1)由题意知:
x≥2,
≤≤ 1≤≤2,
所以A={x|x≥2},B={y|1≤y≤2}.
所以A∩B={2}.
(2)由(1)知B={y|1≤y≤2},
若要使B C,则有a-1≥2,所以a≥3.
【变式训练】求下列函数的定义域:
(1)y=log3(1-x).
(2)y=.
(3)y=log7.
【解析】(1)因为当1-x>0,即x<1时,
函数y=log3(1-x)有意义,
所以函数y=log3(1-x)的定义域为(-∞,1).
(2)由log2x≠0,得x>0且x≠1.
所以函数y=的定义域为{x|x>0且x≠1}.
(3)由>0,得x<.
所以函数y=log7的定义域为.
8.求函数y=log2|x|的定义域,并画出它的图像,由图像指出它的单调区间.
【解题指南】可化为分段函数,利用函数图像的对称特征简化图像的作法.
【解析】函数的定义域为,函数的解析式可化为y=其图像如图
由图像可知,此函数在(0,+∞)上是增函数,在(-∞,0)上是减函数.
【变式训练】画出函数y=|lox|的图像,求使|lox|<1成立的x的取值范围.
【解析】函数y=|lox|的图像如图所示.
|lox|<1等价于-1
对数函数y=log2x的图像和性质
同步测试
(30分钟 50分)
一、选择题(每小题3分,共18分)
1.函数y=lox的反函数是( )
A.y=-()x B.y=()x
C.y=3x
D.y=-3x
【解析】选B.对数函数y=logax的反函数是指数函数y=ax,故函数y=lox的反函数是y=.
【变式训练】函数y=ex的图像与函数y=f(x)的图像关于直线y=x对称,则( )
A.f(x)=lgx
B.f(x)=log2x
C.f(x)=lnx
D.f(x)=xe
【解析】选C.易知y=f(x)是y=ex的反函数,
所以f(x)=lnx.故选C.
2.(2014·郑州高一检测)已知函数f(x)=log2(x+1),若f(α)=1,则α=( )
A.0
B.1
C.2
D.3
【解析】选B.因为f(α)=log2(α+1)=1,所以α+1=2.所以α=1.
3.(2014·温州高一检测)函数y=|log2x|的图像是( )
【解析】选B.函数y=|log2x|的图像过点(1,0),且函数值非负,故选B.
【变式训练】作出函数y=|log2(x+1)|+2的图像.
【解析】第一步:作出y=log2x的图像,如图(1).
第二步:将y=log2x的图像沿x轴向左平移1个单位得y=log2(x+1)的图像,如图(2).
第三步:将y=log2(x+1)的图像在x轴下方的图像以x轴为对称轴翻折到x轴的上方得y=|log2(x+1)|的图像,
如图(3).
第四步:将y=|log2(x+1)|的图像沿y轴方向向上平移2个单位,得到y=|log2(x+1)|+2的图像,如图(4).
4.(2014·重庆高一检测)设f(x)是奇函数,当x>0时,f(x)=log2x,则当x<0时,f(x)等于( )
A.-log2x
B.log2(-x)
C.logx2
D.-log2(-x)
【解题指南】设x<0,然后转化为-x>0,进而借助奇函数求解析式.
【解析】选D.因为x<0,所以-x>0,
所以f(-x)=log2(-x).
又因为f(x)是奇函数,所以f(-x)=-f(x).
所以f(x)=-log2(-x).故选D.
【误区警示】本题在求解过程中常因搞混“x与-x”的转化关系,导致求解错误.
5.(2014·赣州高一检测)函数f(x)=的图像与函数g(x)=log2x图像交点个数是( )
A.1
B.2
C.3
D.4
【解析】选C.函数f(x)与g(x)在同一坐标系内的图像如图所示.
由图像可知,两图像有三个交点.
6.(2014·台州高一检测)已知函数f(x)=|log2x|,正实数m,n且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m,n的值分别为( )
A.,2
B.,
C.,2
D.,4
【解析】选A.如图所示.
由f(m)=f(n)可知,m,n位于1的两侧,
又f(x)在区间[m2,n]上的最大值为2,
所以|log2m2|=2,
所以log2m2=-2,
所以m=.
又f==1,
所以f(n)=log2n=1,所以n=2.
所以m=,n=2.
二、填空题(每小题4分,共12分)
7.(2014·德化高一检测)对数函数f(x)满足f(9)=2,则f(3)= .
【解析】设对数函数为f(x)=logax,所以2=loga9,
所以a=3,所以解析式为y=log3x.
所以f(3)=log33=1.
答案:1
8.已知f(x)=log2x,则f+f= .
【解析】f+f=log2+log2
=log2=-2.
答案:-2
9.(2014·浏阳高一检测)函数f(x)=的定义域为 .
【解题指南】分母不为零,真数大于零,同时成立.
【解析】由解得x<4且x≠3,
所以定义域为{x|x<4且x≠3}.
答案:{x|x<4且x≠3}
【变式训练】(2014·广州高一检测)函数f(x)=+lg(1+x)的定义域是( )
A.(-∞,-1)
B.(1,+∞)
C.(-1,1)∪(1,+∞)
D.(-∞,+∞)
【解析】选C.要使函数有意义,则有
即
所以函数的定义域为(-1,1)∪(1,+∞).
三、解答题(每小题10分,共20分)
10.函数f(x)=(a2-a+1)log(a+1)x是对数函数,求实数a的值.
【解析】因为函数f(x)=(a2-a+1)log(a+1)x是对数函数,
所以a2-a+1=1,解得a=0或a=1.
又a+1>0,a+1≠1,所以a=1.
【误区警示】本题在求解过程中常常因为忘记检验“a+1>0,a+1≠1”而产生增解a=0.
11.利用函数f(x)=log2x的图像和性质解决以下问题:
(1)比较log2与log2的大小.
(2)若log2(2-x)>0,求x的取值范围.
【解析】(1)函数f(x)=log2x在(0,+∞)上为增函数,
又因为>,所以log2>log2.
(2)log2(2-x)>0,即log2(2-x)>log21,
因为函数y=log2x为增函数,
所以2-x>1,所以x<1.
所以x的取值范围为(-∞,1).
(30分钟 50分)
一、选择题(每小题4分,共16分)
1.已知全集U=R,集合A为函数f(x)=ln(x-1)的定义域,则A=( )
A.(-∞,1]
B.[1,+∞)
C.(-∞,2]
D.[2,+∞)
【解析】选A.函数f(x)=ln(x-1)的定义域为{x|x>1},
所以 UA={x|x≤1}.
2.设f(log2x)=2x(x>0),则f(3)=( )
A.128
B.256
C.512
D.8
【解析】选B.令log2x=3,则x=8,所以f(3)=28=256.
【一题多解】令log2x=t,则x=2t,
所以f(t)=,所以f(3)=28=256.
3.(2014·合肥高一检测)若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,其图像经过点(,a),则f(x)=( )
A.log2x
B.lox
C.
D.x2
【解题指南】先求反函数,再借助对数函数的运算性质求a的值,最后求f(x)的解析式.
【解析】选B.因为函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,所以f(x)=logax.
因为f(x)=logax的图像经过点(,a),
所以loga=a a=,即f(x)=lox.
4.(2014·赤峰高一检测)已知f(x)是函数y=log2x的反函数,则y=f(1-x)的图像是( )
【解析】选C.函数y=log2x的反函数为y=2x,故f(x)=2x,于是f(1-x)=21-x=()x-1,此函数在R上为减函数,其图像过点(0,2),所以选项C中的图像符合要求.
二、填空题(每小题5分,共10分)
5.(2014·赣州高一检测)已知函数f(x)=log2(x+1)的值域是[1,2],那么函数f(x)的定义域是 .
【解析】因为f(x)=log2(x+1)的值域为[1,2],
所以1≤log2(x+1)≤2,
所以2≤x+1≤4,即1≤x≤3,
所以f(x)的定义域为[1,3].
答案:[1,3]
【变式训练】若f(x)=则满足f(x)=的x的值为 .
【解题指南】在不同的对应关系下求解x的值,最后求其并集便可.
【解析】因为当x≤1时,f(x)=≥,
所以满足f(x)=的x∈(1,+∞),
即log81x=,所以x==3.
答案:3
6.(2014·天津高一检测)函数f(x)=log2x在区间[a,2a](a>0)上的最大值与最小值之差为 .
【解析】因为f(x)=log2x在区间[a,2a]上是增函数,
所以f(x)max-f(x)min=f(2a)-f(a)=log22a-log2a=log22=1.
答案:1
三、解答题(每小题12分,共24分)
7.(2014·长沙高一检测)已知函数f(x)=的定义域为A,函数g(x)=(-1≤x≤0)的值域为B.
(1)求A∩B.
(2)若C={y|y≤a-1},且B C,求a的取值范围.
【解题指南】由题意列出不等式组,再解不等式组,得出函数的定义域A.再借助指数函数的单调性求集合B.最后借助集合的关系求解(1)(2).
【解析】(1)由题意知:
x≥2,
≤≤ 1≤≤2,
所以A={x|x≥2},B={y|1≤y≤2}.
所以A∩B={2}.
(2)由(1)知B={y|1≤y≤2},
若要使B C,则有a-1≥2,所以a≥3.
【变式训练】求下列函数的定义域:
(1)y=log3(1-x).
(2)y=.
(3)y=log7.
【解析】(1)因为当1-x>0,即x<1时,
函数y=log3(1-x)有意义,
所以函数y=log3(1-x)的定义域为(-∞,1).
(2)由log2x≠0,得x>0且x≠1.
所以函数y=的定义域为{x|x>0且x≠1}.
(3)由>0,得x<.
所以函数y=log7的定义域为.
8.求函数y=log2|x|的定义域,并画出它的图像,由图像指出它的单调区间.
【解题指南】可化为分段函数,利用函数图像的对称特征简化图像的作法.
【解析】函数的定义域为,函数的解析式可化为y=其图像如图
由图像可知,此函数在(0,+∞)上是增函数,在(-∞,0)上是减函数.
【变式训练】画出函数y=|lox|的图像,求使|lox|<1成立的x的取值范围.
【解析】函数y=|lox|的图像如图所示.
|lox|<1等价于-1
