3.5.3 对数函数的图像和性质 学案4(含答案)
文档属性
| 名称 | 3.5.3 对数函数的图像和性质 学案4(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 67.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-14 00:00:00 | ||
图片预览

文档简介
3.5.3
对数函数的图像和性质
学案
课前预习
一、预习目标
记住对数函数的定义;初步把握对数函数的图象与性质.
二、预习内容
1、对数函数的定义_______________________________________.
2、对数函数y
=
logax
(a>0,且a≠
1)的图像和性质
研究函数
和
的图象;
请同学们完成x,y对应值表,并用描点法分别画出函数
和
的图象:
X
…
1
…
…
0
…
…
0
…
观察发现:认真观察函数
y=log2x的图象填写下表:
(表一)
图象特征
代数表述
图象位于y轴的________.
定义域为:
图象向上、向下呈_________趋势.
值域为:
图象自左向右呈___________趋势.
函数在(0,+∞)上是:
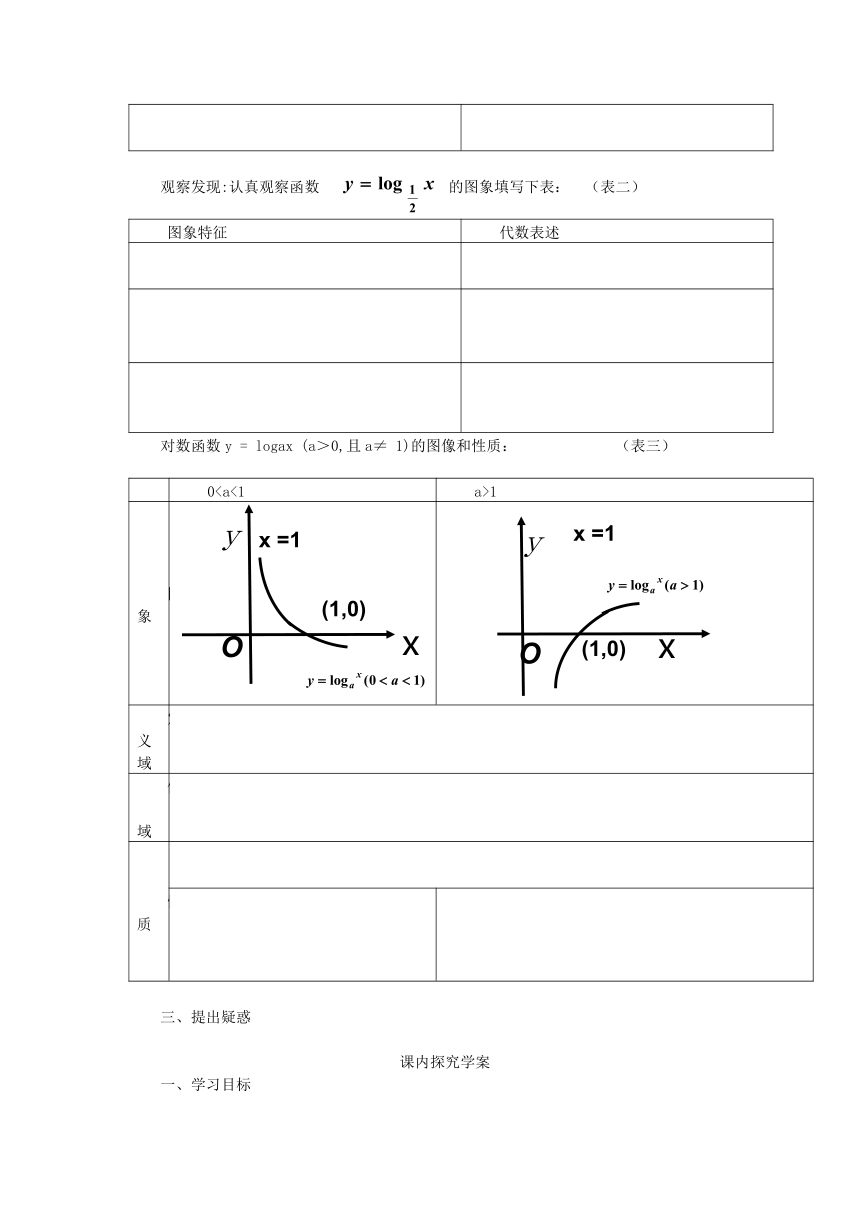
观察发现:认真观察函数
的图象填写下表:
(表二)
图象特征
代数表述
对数函数y
=
logax
(a>0,且a≠
1)的图像和性质:
(表三)
0a>1
图象
定义域
值 域
性质
三、提出疑惑
课内探究学案
一、学习目标
1理解对数函数的概念,熟悉对数函数的图象与性质规律.
2掌握对数函数的性质.
学习重难点
对数函数的图象与性质
二、学习过程
探究点一
例1:求下列函数的定义域:
(1)
;
(2)
.
练习:求下列函数的定义域:
(1)
;
(2)
.
解析
:
直接利用对数函数的定义域求解,而不能先化简.
解:略
点评:本题主要考查了对数函数的定义域极其求法.
探究点二
例2:比较下列各组数中两个值的大小:
(1)
(2)
(3)loga5.1,loga5.9
(a>0,且a≠
1).
(1)
____
;
(2)
____
;
(3)
若
<
,
则m____n;
(4)若
>
,则m____n.
三、反思总结
四、当堂检测
1、求下列函数的定义域
(1)
(2)
2、比较下列各组数中两个值的大小
(1)
(2)
课后练习与提高
1.函数f(x)=lg()是
(奇、偶)函数。
2.已知函数f(x)=log0.5
(-x2+4x+5),则f(3)与f(4)的大小关系为
。
3.已知函数在[0,1]上是减函数,求实数a的取值范围.
y
x
O
x
=1
(1,0)
O
y
x
(1,0)
x
=1
O
y
x
对数函数的图像和性质
学案
课前预习
一、预习目标
记住对数函数的定义;初步把握对数函数的图象与性质.
二、预习内容
1、对数函数的定义_______________________________________.
2、对数函数y
=
logax
(a>0,且a≠
1)的图像和性质
研究函数
和
的图象;
请同学们完成x,y对应值表,并用描点法分别画出函数
和
的图象:
X
…
1
…
…
0
…
…
0
…
观察发现:认真观察函数
y=log2x的图象填写下表:
(表一)
图象特征
代数表述
图象位于y轴的________.
定义域为:
图象向上、向下呈_________趋势.
值域为:
图象自左向右呈___________趋势.
函数在(0,+∞)上是:
观察发现:认真观察函数
的图象填写下表:
(表二)
图象特征
代数表述
对数函数y
=
logax
(a>0,且a≠
1)的图像和性质:
(表三)
0
图象
定义域
值 域
性质
三、提出疑惑
课内探究学案
一、学习目标
1理解对数函数的概念,熟悉对数函数的图象与性质规律.
2掌握对数函数的性质.
学习重难点
对数函数的图象与性质
二、学习过程
探究点一
例1:求下列函数的定义域:
(1)
;
(2)
.
练习:求下列函数的定义域:
(1)
;
(2)
.
解析
:
直接利用对数函数的定义域求解,而不能先化简.
解:略
点评:本题主要考查了对数函数的定义域极其求法.
探究点二
例2:比较下列各组数中两个值的大小:
(1)
(2)
(3)loga5.1,loga5.9
(a>0,且a≠
1).
(1)
____
;
(2)
____
;
(3)
若
<
,
则m____n;
(4)若
>
,则m____n.
三、反思总结
四、当堂检测
1、求下列函数的定义域
(1)
(2)
2、比较下列各组数中两个值的大小
(1)
(2)
课后练习与提高
1.函数f(x)=lg()是
(奇、偶)函数。
2.已知函数f(x)=log0.5
(-x2+4x+5),则f(3)与f(4)的大小关系为
。
3.已知函数在[0,1]上是减函数,求实数a的取值范围.
y
x
O
x
=1
(1,0)
O
y
x
(1,0)
x
=1
O
y
x
