4.1.2 利用二分法求方程的近似解 同步测试(含答案)
文档属性
| 名称 | 4.1.2 利用二分法求方程的近似解 同步测试(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 440.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-13 21:21:41 | ||
图片预览

文档简介
4.1.2利用二分法求方程的近似解
同步测试
一、选择题
1.函数的零点是( )
A.2,-2 B.2
C.-2 D.不存在
2.二次函数有两个不同的零点,则的取值范围是( )
A.(-,-2)
B.
C.
D.
3.函数在区间[-2,4]上的零点必定在区间( )
A. B.
C. D.
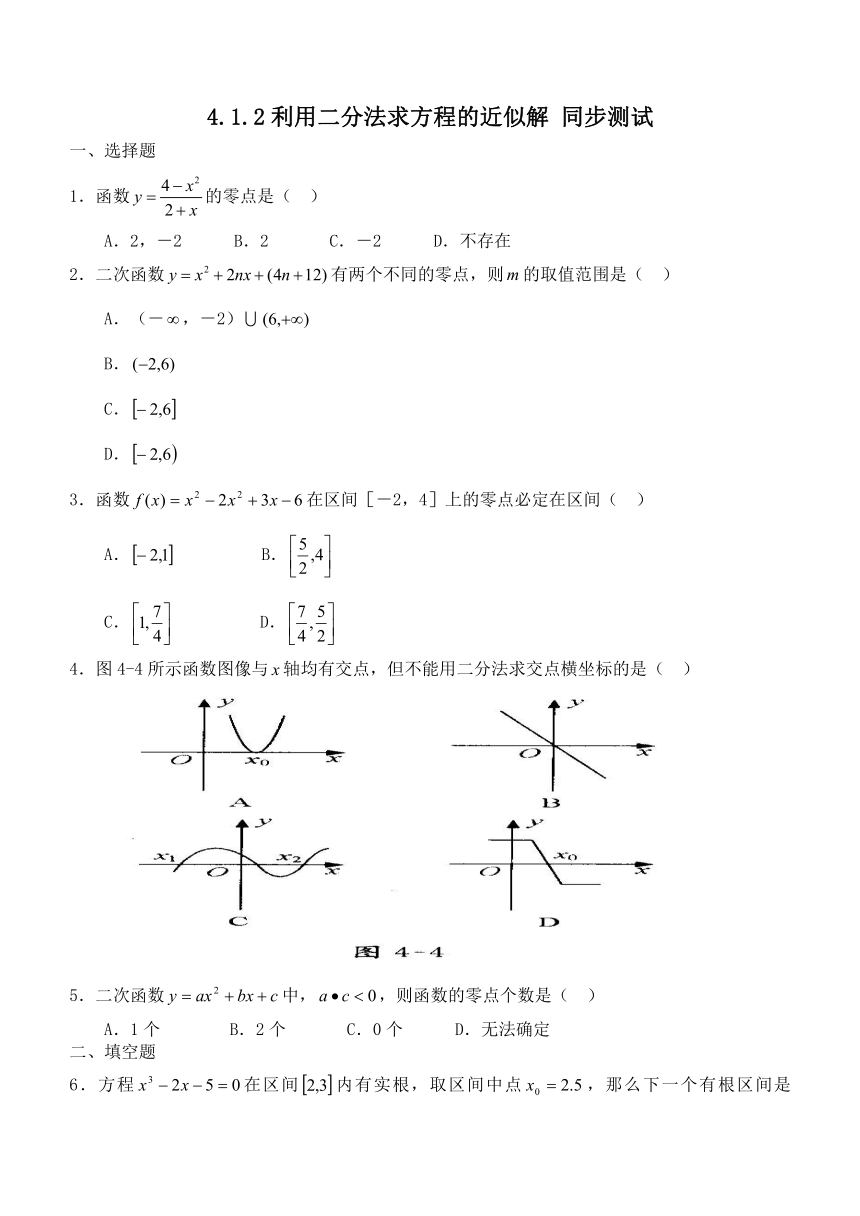
4.图4-4所示函数图像与轴均有交点,但不能用二分法求交点横坐标的是( )
5.二次函数中,,则函数的零点个数是( )
A.1个 B.2个
C.0个 D.无法确定
二、填空题
6.方程在区间内有实根,取区间中点,那么下一个有根区间是________.
7.方程的根__________.(精确到0.1)
三、解答题
8.用二分法求方程的近似解(精确到0.1)
求方程在(2,3)内根的近似值(精确到0.01)
参考答案
1.B
2.A
3.D
4.A
5.B
y
A
O
图
6.[2,2.5](点拨:用二分法)
7.2.6(点拨:用二分法)
8.原方程即2+3x-7=0,令f(x)=21+3x-7,用计算器或
计算机作出函数f(x)=2+3x-7的对应值表,与图像(如
图所示)
234
678
y=2x+3
6|-23102114075142273
观察图像可知∫(1)·f(2)<0,说明
在区间(1,2)内有零点x
取区间(1,2)的中点x1=1.5,用计算
器可得f(1.5)≈-0.87
因此f(1.25)·f(1.5)<0
6810X
所以x0∈(1.25,1,.5)
同理可得x0∈(1.375,1.5),
∈(1.375,1.4375)
第8题图
∵|1.375-1.4375=0.0625<0.1,
区间(1.375,1,4325)的两个端点精确到0.1的近似解都是
1.4,所以原方程精确到0.1的近似值为1.4
r252=-0846因为
)4
f(2.5)·f(3)<0所以零点03
x;∈(2.5,3).
0.1
重复上面的过程,将所得区
22.5/2.6252.753
0.2
间,中点值,中点函数值列成0
4
表并作出图像(如图所示)
0
第9题图
区间
中点值中点的函数值
(2,3)
0.084
(2.5,3)
2.75
.512
(2.5,2.75)
2.625
.215
(2.5,2.625)
2.5625
0.066
(2、5,2.5625)
2.53125
0.009
(2.53125,2.5625)
2.546875
0.029
(2.53125,2.546875)
2.53906250.010
(2.53125,2.5390625)2.535156250.001
∵2.5390625-2.53125=0.0078125<0.01,所以可将
x=2.54作为函数f(x)=1nx+2x-6的零点近似值,也
即方程lnx+2x-6=0根的近似值.
同步测试
一、选择题
1.函数的零点是( )
A.2,-2 B.2
C.-2 D.不存在
2.二次函数有两个不同的零点,则的取值范围是( )
A.(-,-2)
B.
C.
D.
3.函数在区间[-2,4]上的零点必定在区间( )
A. B.
C. D.
4.图4-4所示函数图像与轴均有交点,但不能用二分法求交点横坐标的是( )
5.二次函数中,,则函数的零点个数是( )
A.1个 B.2个
C.0个 D.无法确定
二、填空题
6.方程在区间内有实根,取区间中点,那么下一个有根区间是________.
7.方程的根__________.(精确到0.1)
三、解答题
8.用二分法求方程的近似解(精确到0.1)
求方程在(2,3)内根的近似值(精确到0.01)
参考答案
1.B
2.A
3.D
4.A
5.B
y
A
O
图
6.[2,2.5](点拨:用二分法)
7.2.6(点拨:用二分法)
8.原方程即2+3x-7=0,令f(x)=21+3x-7,用计算器或
计算机作出函数f(x)=2+3x-7的对应值表,与图像(如
图所示)
234
678
y=2x+3
6|-23102114075142273
观察图像可知∫(1)·f(2)<0,说明
在区间(1,2)内有零点x
取区间(1,2)的中点x1=1.5,用计算
器可得f(1.5)≈-0.87
因此f(1.25)·f(1.5)<0
6810X
所以x0∈(1.25,1,.5)
同理可得x0∈(1.375,1.5),
∈(1.375,1.4375)
第8题图
∵|1.375-1.4375=0.0625<0.1,
区间(1.375,1,4325)的两个端点精确到0.1的近似解都是
1.4,所以原方程精确到0.1的近似值为1.4
r252=-0846因为
)4
f(2.5)·f(3)<0所以零点03
x;∈(2.5,3).
0.1
重复上面的过程,将所得区
22.5/2.6252.753
0.2
间,中点值,中点函数值列成0
4
表并作出图像(如图所示)
0
第9题图
区间
中点值中点的函数值
(2,3)
0.084
(2.5,3)
2.75
.512
(2.5,2.75)
2.625
.215
(2.5,2.625)
2.5625
0.066
(2、5,2.5625)
2.53125
0.009
(2.53125,2.5625)
2.546875
0.029
(2.53125,2.546875)
2.53906250.010
(2.53125,2.5390625)2.535156250.001
∵2.5390625-2.53125=0.0078125<0.01,所以可将
x=2.54作为函数f(x)=1nx+2x-6的零点近似值,也
即方程lnx+2x-6=0根的近似值.
