4.1.2 利用二分法求方程的近似解 同步练习(含答案)
文档属性
| 名称 | 4.1.2 利用二分法求方程的近似解 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-14 00:00:00 | ||
图片预览


文档简介
4.1.2
利用二分法求方程的近似解
同步练习
基础巩固
?1.函数f(x)的图像与x轴有3个交点,则方程f(x)=0的实数解的个数是( ).
A.0
B.1
C.2
D.3
2.函数y=x的零点是( ).
A.0
B.(0,0)
C.(1,0)
D.1
3.函数f(x)=的零点一定位于区间( ).
A.
B.(1,2)
C.(2,e)
D.(e,3)
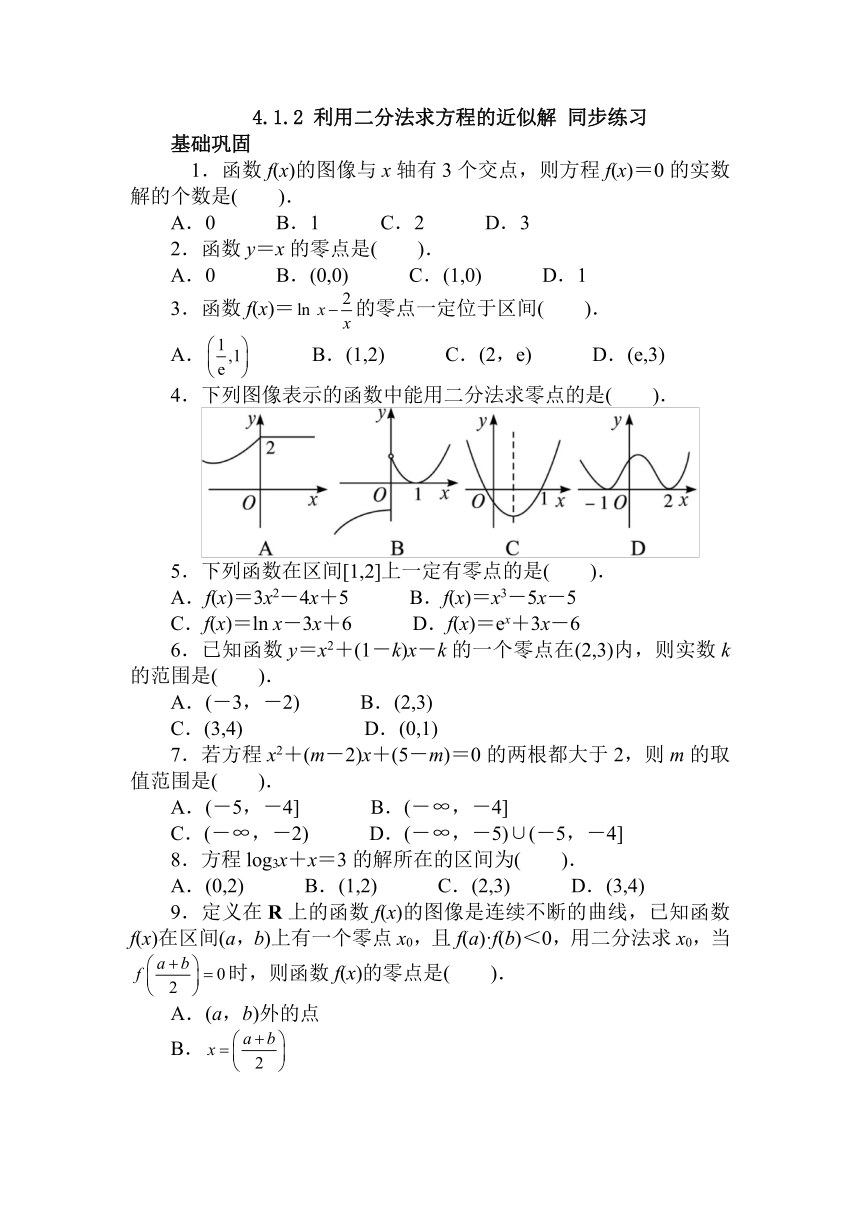
4.下列图像表示的函数中能用二分法求零点的是( ).
5.下列函数在区间[1,2]上一定有零点的是( ).
A.f(x)=3x2-4x+5
B.f(x)=x3-5x-5
C.f(x)=ln
x-3x+6
D.f(x)=ex+3x-6
6.已知函数y=x2+(1-k)x-k的一个零点在(2,3)内,则实数k的范围是( ).
A.(-3,-2)
B.(2,3)
C.(3,4)
D.(0,1)
7.若方程x2+(m-2)x+(5-m)=0的两根都大于2,则m的取值范围是( ).
A.(-5,-4]
B.(-∞,-4]
C.(-∞,-2)
D.(-∞,-5)∪(-5,-4]
8.方程log3x+x=3的解所在的区间为( ).
A.(0,2)
B.(1,2)
C.(2,3)
D.(3,4)
9.定义在R上的函数f(x)的图像是连续不断的曲线,已知函数f(x)在区间(a,b)上有一个零点x0,且f(a)·f(b)<0,用二分法求x0,当时,则函数f(x)的零点是( ).
A.(a,b)外的点
B.
C.区间或内的任意一个实数
D.a或b
10.设f(x)=3x+3x-8,用二分法求方程3x+3x-8=0在(1,2)内近似解的过程中,计算得到f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根落在区间( ).
A.(1,1.25)
B.(1.25,1.5)
C.(1.5,2)
D.不能确定
11.方程(x+1)(x-2)(x+3)+x=0的一个实数解所在的大致区间不可能是( ).
A.[-3,-2]
B.[-2,-1]
C.[0,2]
D.[2,4]
能力提升
12.已知函数f(x)=则函数y=f[f(x)]+1的零点个数是( ).
A.4
B.3
C.2
D.1
13.若函数存在零点,则m的取值范围是________.
14.求方程ln
x+x-3=0在(2,3)内的近似解.(精确到0.1)
15.求证:方程在(0,1)内必有一个实数解.
参考答案
1.D 点拨:因为函数f(x)的图像与x轴有3个交点,所以函数f(x)有3个零点,即方程f(x)=0有3个实数解.
2.A 点拨:函数y=x的零点是其图像与横轴交点的横坐标0,它是一个实数,而不是点,故选A.
3.C 点拨:∵=-1-2e<0,
f(1)=ln
1-=-2<0,
f(2)=ln
2-=ln
2-1=ln
2-ln
e=<0,
f(e)==>0,
∴函数f(x)=的零点一定位于区间(2,e)内.
4.C 点拨:在选项A,B,D中,找不到闭区间[a,b],使得函数在区间[a,b]上的图像是连续曲线,并且在区间端点的函数值符号相反,故选C.
5.D 点拨:对于A,f(1)=4,f(2)=9,f(1)·f(2)>0,无法判断f(x)在[1,2]上是否有零点;对于B,f(1)=-9,f(2)=-7,f(1)·f(2)>0,同选项A一样,无法判断;对于C,f(1)=3,f(2)=ln
2,f(1)·f(2)>0,同选项A,B一样,无法判断;对于D,f(1)=e-3,f(2)=e2,f(1)·f(2)<0,所以f(x)在[1,2]上有零点.
6.B 点拨:Δ=(1-k)2-4×(-k)=(1+k)2.
当Δ=0时,k=-1,二次函数y=x2+2x+1在区间(2,3)内无零点;
当Δ>0时,若函数y=x2+(1-k)x-k的一个零点在(2,3)内,则f(2)·f(3)<0,即(6-3k)·(12-4k)<0,所以(k-2)·(k-3)<0,解得2<k<3,因此,实数k的取值范围是(2,3).
7.A 点拨:考察函数f(x)=x2+(m-2)x+(5-m),由条件知它的两个零点都大于2,其图像如图所示.
由图可知,
即
∴-5<m≤-4.故选A.
8.C 点拨:考察函数f(x)=log3x+x-3,其图像是连续曲线,且f(2)=log32+2-3=<0,f(3)=log33+3-3=1>0,所以,方程log3x+x=3的解所在的区间为(2,3).
9.B
10.B 点拨:∵f(1.25)<0,f(1.5)>0,
∴方程的根落在(1.25,1.5)内.
11.D 点拨:设f(x)=(x+1)(x-2)(x+3)+x,则其图像是连续曲线,又知f(-3)=-3<0,f(-2)=2>0,所以f(x)在[-3,-2]内有零点,即原方程在[-3,-2]内有实数解.同理原方程在[-2,-1],[0,2]内也必有实数解,而在[2,4]上恒有f(x)>0,所以f(x)在[2,4]内没有实数解.
12.A 点拨:由f[f(x)]+1=0可得f[f(x)]=-1,又由f(-2)==-1可得f(x)=-2或f(x)=.若f(x)=-2,则x=-3或;若f(x)=,则或.综上可得y=f[f(x)]+1有4个零点.
13.[-1,0) 点拨:(方法1)函数的图像可以看作的图像向上或向下平移|m|个单位长度得到的.若函数存在零点,则m的取值范围是[-1,0).
(方法2)若函数存在零点,则方程,即有实数解.
∵|1-x|≥0,
∴,
∴-1≤m<0.
14.解:令f(x)=ln
x+x-3,
f(2)=ln
2-1=<0,f(3)=ln
3>0,
用二分法得方程ln
x+x-3=0的有解区间如下表:
次数
左端点
左端点函数值
右端点
右端点函数值
区间长度
第1次
2
-0.306
9
3
1.098
6
1
第2次
2
-0.306
9
2.5
0.416
3
0.5
第3次
2
-0.306
9
2.25
0.060
9
0.25
第4次
2.125
-0.121
2
2.25
0.060
9
0.125
第5次
2.187
5
-0.029
7
2.25
0.060
9
0.062
5
因为区间[2.187
5,2.25]的区间长度为0.062
5,它小于0.1,因此,这一区间内的任意一个数都可以作为方程ln
x+x-3=0的近似解,如2.2.
15.证明:考察函数f(x)=,即f(x)=,易知函数f(x)在[0,1]上是增函数.
∵f(0)=30-=-1<0,f(1)=,即f(0)·f(1)<0,
∴函数f(x)在区间(0,1)内有且只有一个零点,
即方程在(0,1)内必有一个实数解.
利用二分法求方程的近似解
同步练习
基础巩固
?1.函数f(x)的图像与x轴有3个交点,则方程f(x)=0的实数解的个数是( ).
A.0
B.1
C.2
D.3
2.函数y=x的零点是( ).
A.0
B.(0,0)
C.(1,0)
D.1
3.函数f(x)=的零点一定位于区间( ).
A.
B.(1,2)
C.(2,e)
D.(e,3)
4.下列图像表示的函数中能用二分法求零点的是( ).
5.下列函数在区间[1,2]上一定有零点的是( ).
A.f(x)=3x2-4x+5
B.f(x)=x3-5x-5
C.f(x)=ln
x-3x+6
D.f(x)=ex+3x-6
6.已知函数y=x2+(1-k)x-k的一个零点在(2,3)内,则实数k的范围是( ).
A.(-3,-2)
B.(2,3)
C.(3,4)
D.(0,1)
7.若方程x2+(m-2)x+(5-m)=0的两根都大于2,则m的取值范围是( ).
A.(-5,-4]
B.(-∞,-4]
C.(-∞,-2)
D.(-∞,-5)∪(-5,-4]
8.方程log3x+x=3的解所在的区间为( ).
A.(0,2)
B.(1,2)
C.(2,3)
D.(3,4)
9.定义在R上的函数f(x)的图像是连续不断的曲线,已知函数f(x)在区间(a,b)上有一个零点x0,且f(a)·f(b)<0,用二分法求x0,当时,则函数f(x)的零点是( ).
A.(a,b)外的点
B.
C.区间或内的任意一个实数
D.a或b
10.设f(x)=3x+3x-8,用二分法求方程3x+3x-8=0在(1,2)内近似解的过程中,计算得到f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根落在区间( ).
A.(1,1.25)
B.(1.25,1.5)
C.(1.5,2)
D.不能确定
11.方程(x+1)(x-2)(x+3)+x=0的一个实数解所在的大致区间不可能是( ).
A.[-3,-2]
B.[-2,-1]
C.[0,2]
D.[2,4]
能力提升
12.已知函数f(x)=则函数y=f[f(x)]+1的零点个数是( ).
A.4
B.3
C.2
D.1
13.若函数存在零点,则m的取值范围是________.
14.求方程ln
x+x-3=0在(2,3)内的近似解.(精确到0.1)
15.求证:方程在(0,1)内必有一个实数解.
参考答案
1.D 点拨:因为函数f(x)的图像与x轴有3个交点,所以函数f(x)有3个零点,即方程f(x)=0有3个实数解.
2.A 点拨:函数y=x的零点是其图像与横轴交点的横坐标0,它是一个实数,而不是点,故选A.
3.C 点拨:∵=-1-2e<0,
f(1)=ln
1-=-2<0,
f(2)=ln
2-=ln
2-1=ln
2-ln
e=<0,
f(e)==>0,
∴函数f(x)=的零点一定位于区间(2,e)内.
4.C 点拨:在选项A,B,D中,找不到闭区间[a,b],使得函数在区间[a,b]上的图像是连续曲线,并且在区间端点的函数值符号相反,故选C.
5.D 点拨:对于A,f(1)=4,f(2)=9,f(1)·f(2)>0,无法判断f(x)在[1,2]上是否有零点;对于B,f(1)=-9,f(2)=-7,f(1)·f(2)>0,同选项A一样,无法判断;对于C,f(1)=3,f(2)=ln
2,f(1)·f(2)>0,同选项A,B一样,无法判断;对于D,f(1)=e-3,f(2)=e2,f(1)·f(2)<0,所以f(x)在[1,2]上有零点.
6.B 点拨:Δ=(1-k)2-4×(-k)=(1+k)2.
当Δ=0时,k=-1,二次函数y=x2+2x+1在区间(2,3)内无零点;
当Δ>0时,若函数y=x2+(1-k)x-k的一个零点在(2,3)内,则f(2)·f(3)<0,即(6-3k)·(12-4k)<0,所以(k-2)·(k-3)<0,解得2<k<3,因此,实数k的取值范围是(2,3).
7.A 点拨:考察函数f(x)=x2+(m-2)x+(5-m),由条件知它的两个零点都大于2,其图像如图所示.
由图可知,
即
∴-5<m≤-4.故选A.
8.C 点拨:考察函数f(x)=log3x+x-3,其图像是连续曲线,且f(2)=log32+2-3=<0,f(3)=log33+3-3=1>0,所以,方程log3x+x=3的解所在的区间为(2,3).
9.B
10.B 点拨:∵f(1.25)<0,f(1.5)>0,
∴方程的根落在(1.25,1.5)内.
11.D 点拨:设f(x)=(x+1)(x-2)(x+3)+x,则其图像是连续曲线,又知f(-3)=-3<0,f(-2)=2>0,所以f(x)在[-3,-2]内有零点,即原方程在[-3,-2]内有实数解.同理原方程在[-2,-1],[0,2]内也必有实数解,而在[2,4]上恒有f(x)>0,所以f(x)在[2,4]内没有实数解.
12.A 点拨:由f[f(x)]+1=0可得f[f(x)]=-1,又由f(-2)==-1可得f(x)=-2或f(x)=.若f(x)=-2,则x=-3或;若f(x)=,则或.综上可得y=f[f(x)]+1有4个零点.
13.[-1,0) 点拨:(方法1)函数的图像可以看作的图像向上或向下平移|m|个单位长度得到的.若函数存在零点,则m的取值范围是[-1,0).
(方法2)若函数存在零点,则方程,即有实数解.
∵|1-x|≥0,
∴,
∴-1≤m<0.
14.解:令f(x)=ln
x+x-3,
f(2)=ln
2-1=<0,f(3)=ln
3>0,
用二分法得方程ln
x+x-3=0的有解区间如下表:
次数
左端点
左端点函数值
右端点
右端点函数值
区间长度
第1次
2
-0.306
9
3
1.098
6
1
第2次
2
-0.306
9
2.5
0.416
3
0.5
第3次
2
-0.306
9
2.25
0.060
9
0.25
第4次
2.125
-0.121
2
2.25
0.060
9
0.125
第5次
2.187
5
-0.029
7
2.25
0.060
9
0.062
5
因为区间[2.187
5,2.25]的区间长度为0.062
5,它小于0.1,因此,这一区间内的任意一个数都可以作为方程ln
x+x-3=0的近似解,如2.2.
15.证明:考察函数f(x)=,即f(x)=,易知函数f(x)在[0,1]上是增函数.
∵f(0)=30-=-1<0,f(1)=,即f(0)·f(1)<0,
∴函数f(x)在区间(0,1)内有且只有一个零点,
即方程在(0,1)内必有一个实数解.
