4.2.1 实际问题的函数刻画 同步练习(含答案)
文档属性
| 名称 | 4.2.1 实际问题的函数刻画 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 89.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-13 00:00:00 | ||
图片预览



文档简介
4.2.1
实际问题的函数刻画
( file: / / / D:\\TDDOWNLOAD\\各科教材\\成才之路·北师大版数学必修1\\4-2.ppt"
\t
"_parent )
( file: / / / D:\\TDDOWNLOAD\\各科教材\\成才之路·北师大版数学必修1\\4-2.ppt"
\t
"_parent )
同步练习
一、选择题
1.生产一定数量商品的全部费用称为生产成本,它可以表示为商品数量的函数,现知一企业生产某种商品的数量为x件时的成本函数为c(x)=20+2x+x2(万元),若售出一件商品收入是20万元,那么该企业为获取最大利润,应生产这种商品的数量为( )
A.18件
B.36件
C.22件
D.9件
[答案] A
[解析] y=20x-c(x)=20x-20-2x-x2=-x2+18x-20.∴x=18时,y有最大值.
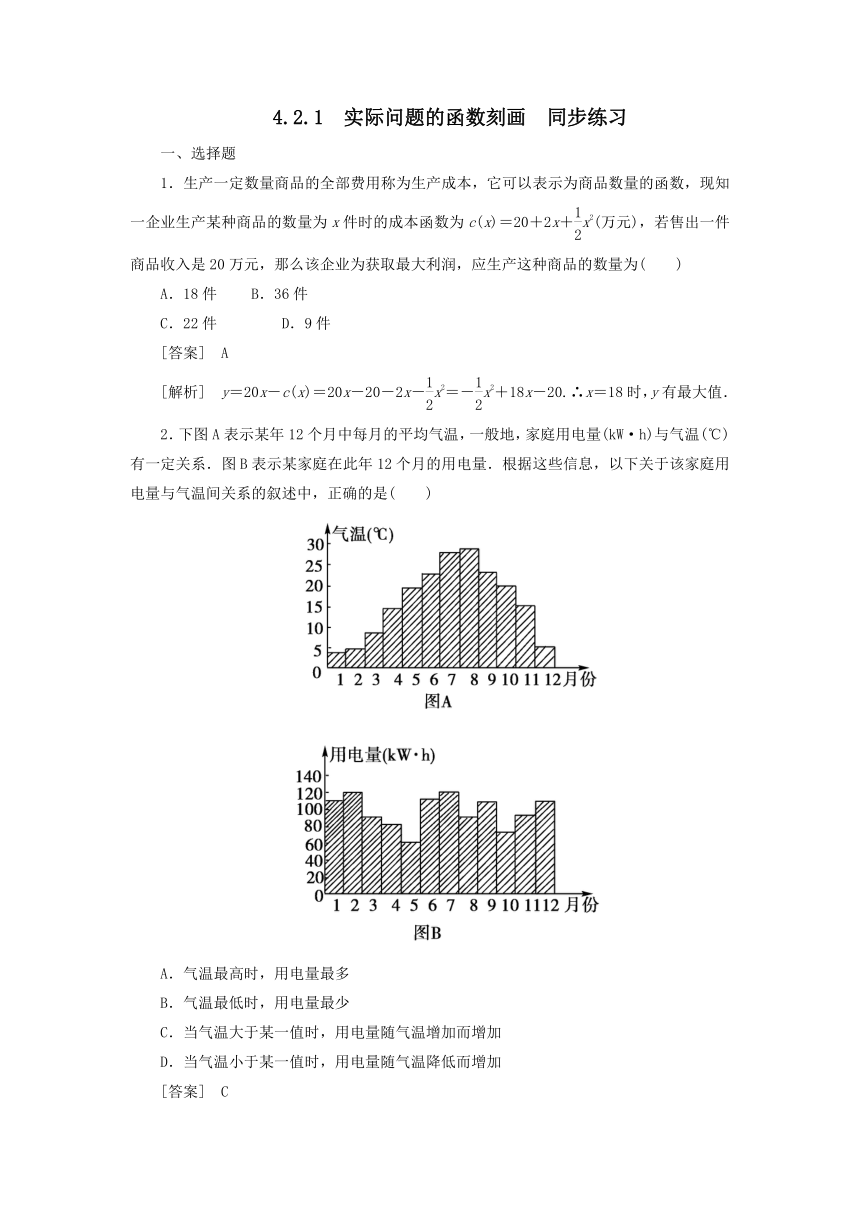
2.下图A表示某年12个月中每月的平均气温,一般地,家庭用电量(kW·h)与气温(℃)有一定关系.图B表示某家庭在此年12个月的用电量.根据这些信息,以下关于该家庭用电量与气温间关系的叙述中,正确的是( )
A.气温最高时,用电量最多
B.气温最低时,用电量最少
C.当气温大于某一值时,用电量随气温增加而增加
D.当气温小于某一值时,用电量随气温降低而增加
[答案] C
[解析] 逐月分析图像的升降趋势和变化率,排除干扰选项便能确定答案.
比较两图可以发现,2月份用电量最多,而2月份气温不是最高,因此排除A.同理可排除B.
8月至12月份气温一直下降,但用电量有增有减,排除D.
由5、6、7三个月的气温和用电量可得出C正确.故选C.
3.在我国大西北,某地区荒漠化土地面积每年平均比上一年增长10.4%,专家预测经过x年可能增长为原来的y倍,则函数y=f(x)的图像大致为( )
[答案] D
[解析] 设原来的荒漠化土地面积为a,则ay=a(1+10.4%)x,即y=1.104x(x≥0).
4.2002年3月5日,第九届全国人民代表大会第五次会议《政府工作报告》指出:2001年,国内生产总值达到95933亿元,比上年增长7.3%.如果“十五”期间(2001年~2005年)每年我国生产总值按此年增长,那么到“十五”末我国国内生产总值约为( )
A.115000亿元
B.120000亿元
C.127000亿元
D.135000亿元
[答案] C
[解析] 由于2001年生产总值已达95933亿元,则从2001年底到2005年底中时间只有4年,故x=4.
则y=95933×(1+7.3%)4≈127000亿元.
5.某个企业的一个车间有8名工人,以往每人年薪为1万元.从今年起,计划每人的年薪比上一年增加10%,另外每年新招3名工人,每名新工人的第一年年薪为8千元,第二年起与老工人的年薪相同.若以今年为第一年,那么第x年企业付给工人的工资总额y(万元)表示成x的函数,其表达式为( )
A.y=(3x+5)1.1x+2.4
B.y=8×1.1x+2.4x
C.y=(3x+8)1.1x+2.4
D.y=(3x+5)1.1x-1+2.4
[答案] A
[解析] 第一年企业付给工人的工资总额为8×1.1+3×0.8(万元),
第二年应付给工人的工资总额为(8+3)×1.12+3×0.8(万元),
依次类推:第x年企业付给工人的工资总额应为y=[8+3(x-1)]×1.1x+2.4=(3x+5)×1.1x+2.4.
6.据报道,青海湖的湖水在最近50年内减少了10%,如果按此规律,设2012年有湖水量为m,从2012年起,过x年后湖水量y与x的函数关系式为( )
A.y=0.9
B.y=(1-0.1)m
C.y=0.9·m
D.y=(1-0.150x)m
[答案] C
[解析] 湖水剩余量y与年数x构成指数函数关系,y=0.9m.
二、填空题
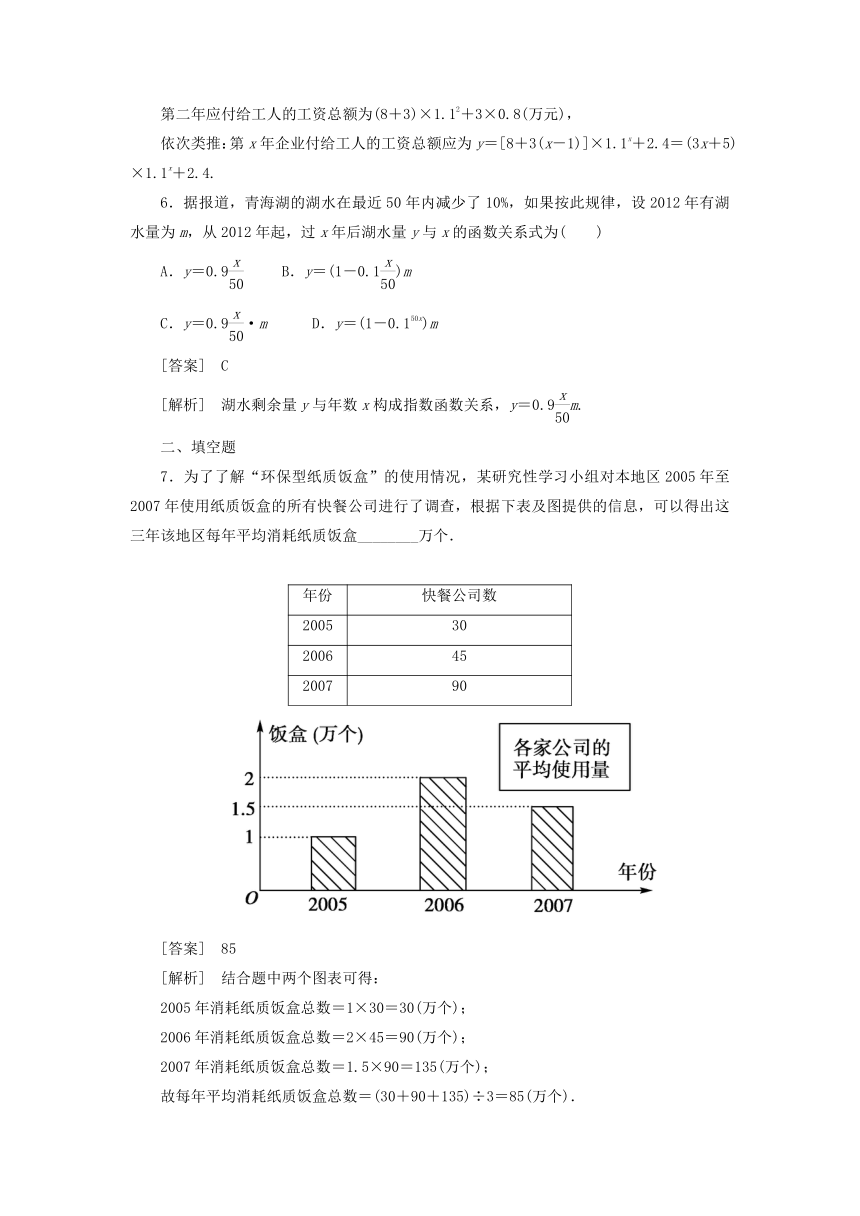
7.为了了解“环保型纸质饭盒”的使用情况,某研究性学习小组对本地区2005年至2007年使用纸质饭盒的所有快餐公司进行了调查,根据下表及图提供的信息,可以得出这三年该地区每年平均消耗纸质饭盒________万个.
年份
快餐公司数
2005
30
2006
45
2007
90
[答案] 85
[解析] 结合题中两个图表可得:
2005年消耗纸质饭盒总数=1×30=30(万个);
2006年消耗纸质饭盒总数=2×45=90(万个);
2007年消耗纸质饭盒总数=1.5×90=135(万个);
故每年平均消耗纸质饭盒总数=(30+90+135)÷3=85(万个).
8.某公司欲投资13亿元进行项目开发,现有以下6个项目可供选择:
项目
A
B
C
D
E
F
投资额(亿元)
5
2
6
4
6
1
利润(亿元)
0.55
0.4
0.6
0.5
0.9
0.1
设计一个投资方案,使投资13亿元所获利润大于1.6亿元,则应选的项目是______.(只需写出项目的代号)
[答案] A、B、E或B、D、E、F
[解析] 当投资为13亿元时,有以下两种投资选择方案:f(A,B,E)=0.55+0.4+0.9=1.85(投资13亿元);
f(B,D,E,F)=0.4+0.5+0.9+0.1=1.9(投资13亿元).
三、解答题
9.某化工厂生产一种溶液,按市场要求,杂质含量不能超过1‰,若初时含杂质2%,每过滤一次可使杂质含量减少,问至少应过滤几次才能使产品达到市场要求?(已知:lg2=0.3010,lg3=0.4771)
[解析] 解法一:∵每次过滤杂质含量降为原来的,过滤n次后杂质含量为·n.
依题意,得·n≤,即n≤,
∵7=>,8=<,
∴由题意知至少应过滤8次才能使产品达到市场要求.
解法二:接解法一:()n≤,
则n(lg2-lg3)≤-(1+lg2),
即n≥≈7.4,又n∈N+,
∴n≥8,即至少应过滤8次才能使产品达到市场要求.
能
力
提
升
一、选择题
1.
如右图所示的是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at,有以下叙述:
①这个指数函数的底数为2;
②第5个月时,浮萍面积就会超过30m2;
③浮萍从4m2蔓延到12m2只需1.5个月;
④浮萍每月增加的面积都相等;
⑤若浮萍蔓延到2m2、4m2、8m2所经过的时间分别为t1、t2、t3,则t1+t2=t3.
其中正确的是( )
A.①②
B.①②③④
C.②③④⑤
D.①②⑤
[答案] D
[解析] 设此指数函数为y=ax(a>0且a≠1),
由图像可知:(1,2),(2,4)代入可得:
a=2,∴y=2x,故①正确.
当x=5时,y=25=32>30,②正确.
当y=4时,x=2,当y=12时,x=log212>log22,从而可知浮萍从4m2蔓延到12m2用时超过1.5个月,③错,显然④错误.
把y=2,4,8代入y=2t分别得t1=1,t2=2,t3=3,故⑤正确.因此选D.
2.用清水洗衣服,若每次能洗去污垢的,要使存留的污垢不超过1%,则至少要洗的次数是( )
A.3 B.4 C.5 D.6
[答案] B
[解析] 设至少要洗x次,则(1-)x≤,
∴x≥≈3.321,因此需4次.
二、填空题
3.伦敦市为成功举办2012年奥运会,决定从2008年底到2011年底三年间更新市内全部出租车,若每年更新的车辆数比前一年递增10%,则2009年底已更新现有总车辆数的百分比约为________(保留3位有效数字).
[答案] 30.2%
[解析] 设现有车辆总数为a,2009年底更新了现有总车辆数的百分比为x,则a·x+a·x(1+10%)+ax(1+10%)2=a.
∴x(1+1.1+1.12)=1.
∴x≈30.2%.
4.为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为y=t-a(a为常数),如图所示.根据图中提供的信息,回答下列问题:
(1)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为________________;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过________小时后,学生才能回到教室.
[答案] (1)y=;(2)0.6.
[解析] 由图像可知,当0≤t<0.1时,y=10t;
当t<0.1时,由1=0.1-a,得a=0.1,
∴当t>0.1时,y=t-.
∴y=,
由题意可知()t-<0.25,得t>0.6(小时).
三、解答题
5.某工厂生产商品A,每件售价80元,每年产销80万件,工厂为了开发新产品,经过市场调查,决定提出商品A的销售金额的p%作为新产品开发费(即每销售100元提出p元),并将商品A的年产销量减少了10p万件.
(1)若工厂提出的新产品开发费不少于96万元,求p的取值范围;
(2)若工厂仅考虑每年提出最高的开发费,求此时p的值.
[解析] 由题意知,当开发费是商品A的销售金额的p%时,销售量为(80-10p)万件,此时销售金额为80×(80-10p)万元,
新产品开发金额f(p)=80×(80-10p)×p%(万元).
(1)由题设知
解得2≤p≤6.
即新产品开发费不少于96万元时,p的取值范围为2≤p≤6.
(2)当0=-8(p-4)2+128.
∴当p=4时,f(p)max=128.
即当p=4时,开发金额最多,可达到128万元.
6.要在墙上开一个上部为半圆,下部为矩形的窗户(如图所示),在窗框为定长l的条件下,要使窗户透光面积最大,窗户应具有怎样的尺寸?
[解析] 设半圆的直径为x,矩形的高度为y,窗户透光面积为S,则窗框总长l=+x+2y,
y=,由y>0,得x∈(0,).
S=x2+xy=x2+·x
=-(x-)2+,x∈(0,).
当x=时,Smax=,此时,y==.
答:窗户中的矩形高为,且半径等于矩形的高时,窗户的透光面积最大.
7.某工厂今年1月、2月、3月生产某种产品分别为1万件、1.2万件、1.3万件.为了估计以后每个月的产量,以这三个月的产品数量为依据,用一个函数来模拟该产品的月产量y与月份x的关系.模拟函数可以选择二次函数或函数y=a·bx+c(其中a,b,c为常数),已知4月份该产品的产量为1.37万件,试问用以上哪个函数作为模拟函数较好?并说明理由.
[解析] 设两个函数
y1=f(x)=px2+qx+r(p≠0);
y2=g(x)=a·bx+c.
依题意,有解得
∴y1=f(x)=-0.05x2+0.35x+0.7,
∴f(4)=1.3(万件),
依题意,也有解得
∴y2=g(x)=-0.8×(0.5)x+1.4,
g(4)=-0.8×(0.5)4+1.4=1.35(万件).
经比较可知,g(4)=1.35(万件),比f(4)=1.3(万件)更接近于4月份的产量1.37万件.
∴选用y2=g(x)=-0.8×(0.5)x+1.4作为模拟函数较好.
实际问题的函数刻画
( file: / / / D:\\TDDOWNLOAD\\各科教材\\成才之路·北师大版数学必修1\\4-2.ppt"
\t
"_parent )
( file: / / / D:\\TDDOWNLOAD\\各科教材\\成才之路·北师大版数学必修1\\4-2.ppt"
\t
"_parent )
同步练习
一、选择题
1.生产一定数量商品的全部费用称为生产成本,它可以表示为商品数量的函数,现知一企业生产某种商品的数量为x件时的成本函数为c(x)=20+2x+x2(万元),若售出一件商品收入是20万元,那么该企业为获取最大利润,应生产这种商品的数量为( )
A.18件
B.36件
C.22件
D.9件
[答案] A
[解析] y=20x-c(x)=20x-20-2x-x2=-x2+18x-20.∴x=18时,y有最大值.
2.下图A表示某年12个月中每月的平均气温,一般地,家庭用电量(kW·h)与气温(℃)有一定关系.图B表示某家庭在此年12个月的用电量.根据这些信息,以下关于该家庭用电量与气温间关系的叙述中,正确的是( )
A.气温最高时,用电量最多
B.气温最低时,用电量最少
C.当气温大于某一值时,用电量随气温增加而增加
D.当气温小于某一值时,用电量随气温降低而增加
[答案] C
[解析] 逐月分析图像的升降趋势和变化率,排除干扰选项便能确定答案.
比较两图可以发现,2月份用电量最多,而2月份气温不是最高,因此排除A.同理可排除B.
8月至12月份气温一直下降,但用电量有增有减,排除D.
由5、6、7三个月的气温和用电量可得出C正确.故选C.
3.在我国大西北,某地区荒漠化土地面积每年平均比上一年增长10.4%,专家预测经过x年可能增长为原来的y倍,则函数y=f(x)的图像大致为( )
[答案] D
[解析] 设原来的荒漠化土地面积为a,则ay=a(1+10.4%)x,即y=1.104x(x≥0).
4.2002年3月5日,第九届全国人民代表大会第五次会议《政府工作报告》指出:2001年,国内生产总值达到95933亿元,比上年增长7.3%.如果“十五”期间(2001年~2005年)每年我国生产总值按此年增长,那么到“十五”末我国国内生产总值约为( )
A.115000亿元
B.120000亿元
C.127000亿元
D.135000亿元
[答案] C
[解析] 由于2001年生产总值已达95933亿元,则从2001年底到2005年底中时间只有4年,故x=4.
则y=95933×(1+7.3%)4≈127000亿元.
5.某个企业的一个车间有8名工人,以往每人年薪为1万元.从今年起,计划每人的年薪比上一年增加10%,另外每年新招3名工人,每名新工人的第一年年薪为8千元,第二年起与老工人的年薪相同.若以今年为第一年,那么第x年企业付给工人的工资总额y(万元)表示成x的函数,其表达式为( )
A.y=(3x+5)1.1x+2.4
B.y=8×1.1x+2.4x
C.y=(3x+8)1.1x+2.4
D.y=(3x+5)1.1x-1+2.4
[答案] A
[解析] 第一年企业付给工人的工资总额为8×1.1+3×0.8(万元),
第二年应付给工人的工资总额为(8+3)×1.12+3×0.8(万元),
依次类推:第x年企业付给工人的工资总额应为y=[8+3(x-1)]×1.1x+2.4=(3x+5)×1.1x+2.4.
6.据报道,青海湖的湖水在最近50年内减少了10%,如果按此规律,设2012年有湖水量为m,从2012年起,过x年后湖水量y与x的函数关系式为( )
A.y=0.9
B.y=(1-0.1)m
C.y=0.9·m
D.y=(1-0.150x)m
[答案] C
[解析] 湖水剩余量y与年数x构成指数函数关系,y=0.9m.
二、填空题
7.为了了解“环保型纸质饭盒”的使用情况,某研究性学习小组对本地区2005年至2007年使用纸质饭盒的所有快餐公司进行了调查,根据下表及图提供的信息,可以得出这三年该地区每年平均消耗纸质饭盒________万个.
年份
快餐公司数
2005
30
2006
45
2007
90
[答案] 85
[解析] 结合题中两个图表可得:
2005年消耗纸质饭盒总数=1×30=30(万个);
2006年消耗纸质饭盒总数=2×45=90(万个);
2007年消耗纸质饭盒总数=1.5×90=135(万个);
故每年平均消耗纸质饭盒总数=(30+90+135)÷3=85(万个).
8.某公司欲投资13亿元进行项目开发,现有以下6个项目可供选择:
项目
A
B
C
D
E
F
投资额(亿元)
5
2
6
4
6
1
利润(亿元)
0.55
0.4
0.6
0.5
0.9
0.1
设计一个投资方案,使投资13亿元所获利润大于1.6亿元,则应选的项目是______.(只需写出项目的代号)
[答案] A、B、E或B、D、E、F
[解析] 当投资为13亿元时,有以下两种投资选择方案:f(A,B,E)=0.55+0.4+0.9=1.85(投资13亿元);
f(B,D,E,F)=0.4+0.5+0.9+0.1=1.9(投资13亿元).
三、解答题
9.某化工厂生产一种溶液,按市场要求,杂质含量不能超过1‰,若初时含杂质2%,每过滤一次可使杂质含量减少,问至少应过滤几次才能使产品达到市场要求?(已知:lg2=0.3010,lg3=0.4771)
[解析] 解法一:∵每次过滤杂质含量降为原来的,过滤n次后杂质含量为·n.
依题意,得·n≤,即n≤,
∵7=>,8=<,
∴由题意知至少应过滤8次才能使产品达到市场要求.
解法二:接解法一:()n≤,
则n(lg2-lg3)≤-(1+lg2),
即n≥≈7.4,又n∈N+,
∴n≥8,即至少应过滤8次才能使产品达到市场要求.
能
力
提
升
一、选择题
1.
如右图所示的是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at,有以下叙述:
①这个指数函数的底数为2;
②第5个月时,浮萍面积就会超过30m2;
③浮萍从4m2蔓延到12m2只需1.5个月;
④浮萍每月增加的面积都相等;
⑤若浮萍蔓延到2m2、4m2、8m2所经过的时间分别为t1、t2、t3,则t1+t2=t3.
其中正确的是( )
A.①②
B.①②③④
C.②③④⑤
D.①②⑤
[答案] D
[解析] 设此指数函数为y=ax(a>0且a≠1),
由图像可知:(1,2),(2,4)代入可得:
a=2,∴y=2x,故①正确.
当x=5时,y=25=32>30,②正确.
当y=4时,x=2,当y=12时,x=log212>log22,从而可知浮萍从4m2蔓延到12m2用时超过1.5个月,③错,显然④错误.
把y=2,4,8代入y=2t分别得t1=1,t2=2,t3=3,故⑤正确.因此选D.
2.用清水洗衣服,若每次能洗去污垢的,要使存留的污垢不超过1%,则至少要洗的次数是( )
A.3 B.4 C.5 D.6
[答案] B
[解析] 设至少要洗x次,则(1-)x≤,
∴x≥≈3.321,因此需4次.
二、填空题
3.伦敦市为成功举办2012年奥运会,决定从2008年底到2011年底三年间更新市内全部出租车,若每年更新的车辆数比前一年递增10%,则2009年底已更新现有总车辆数的百分比约为________(保留3位有效数字).
[答案] 30.2%
[解析] 设现有车辆总数为a,2009年底更新了现有总车辆数的百分比为x,则a·x+a·x(1+10%)+ax(1+10%)2=a.
∴x(1+1.1+1.12)=1.
∴x≈30.2%.
4.为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为y=t-a(a为常数),如图所示.根据图中提供的信息,回答下列问题:
(1)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为________________;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过________小时后,学生才能回到教室.
[答案] (1)y=;(2)0.6.
[解析] 由图像可知,当0≤t<0.1时,y=10t;
当t<0.1时,由1=0.1-a,得a=0.1,
∴当t>0.1时,y=t-.
∴y=,
由题意可知()t-<0.25,得t>0.6(小时).
三、解答题
5.某工厂生产商品A,每件售价80元,每年产销80万件,工厂为了开发新产品,经过市场调查,决定提出商品A的销售金额的p%作为新产品开发费(即每销售100元提出p元),并将商品A的年产销量减少了10p万件.
(1)若工厂提出的新产品开发费不少于96万元,求p的取值范围;
(2)若工厂仅考虑每年提出最高的开发费,求此时p的值.
[解析] 由题意知,当开发费是商品A的销售金额的p%时,销售量为(80-10p)万件,此时销售金额为80×(80-10p)万元,
新产品开发金额f(p)=80×(80-10p)×p%(万元).
(1)由题设知
解得2≤p≤6.
即新产品开发费不少于96万元时,p的取值范围为2≤p≤6.
(2)当0
∴当p=4时,f(p)max=128.
即当p=4时,开发金额最多,可达到128万元.
6.要在墙上开一个上部为半圆,下部为矩形的窗户(如图所示),在窗框为定长l的条件下,要使窗户透光面积最大,窗户应具有怎样的尺寸?
[解析] 设半圆的直径为x,矩形的高度为y,窗户透光面积为S,则窗框总长l=+x+2y,
y=,由y>0,得x∈(0,).
S=x2+xy=x2+·x
=-(x-)2+,x∈(0,).
当x=时,Smax=,此时,y==.
答:窗户中的矩形高为,且半径等于矩形的高时,窗户的透光面积最大.
7.某工厂今年1月、2月、3月生产某种产品分别为1万件、1.2万件、1.3万件.为了估计以后每个月的产量,以这三个月的产品数量为依据,用一个函数来模拟该产品的月产量y与月份x的关系.模拟函数可以选择二次函数或函数y=a·bx+c(其中a,b,c为常数),已知4月份该产品的产量为1.37万件,试问用以上哪个函数作为模拟函数较好?并说明理由.
[解析] 设两个函数
y1=f(x)=px2+qx+r(p≠0);
y2=g(x)=a·bx+c.
依题意,有解得
∴y1=f(x)=-0.05x2+0.35x+0.7,
∴f(4)=1.3(万件),
依题意,也有解得
∴y2=g(x)=-0.8×(0.5)x+1.4,
g(4)=-0.8×(0.5)4+1.4=1.35(万件).
经比较可知,g(4)=1.35(万件),比f(4)=1.3(万件)更接近于4月份的产量1.37万件.
∴选用y2=g(x)=-0.8×(0.5)x+1.4作为模拟函数较好.
