4.2.1 实际问题的函数刻画 同步训练(含答案)
文档属性
| 名称 | 4.2.1 实际问题的函数刻画 同步训练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 266.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-14 00:00:00 | ||
图片预览


文档简介
4.2.1
实际问题的函数刻画
同步训练
(30分钟
50分)
一、选择题(每小题4分,共16分)
1.某种生物增长的数量y与时间x的关系如下表:
下面函数关系式中,能表达这种关系的是(
)
(A)y=x2-1
(B)y=2x-1
(C)y=2x-1
(D)y=1.5x2-2.5x+2
2.一种放射性物质不断变化为其他物质,每经过一年,剩余的物质为原来的,则经过多少年,剩余的物质是原来的
(
)
(A)5
(B)4
(C)3
(D)2
3.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为:
y=,其中,x代表拟录用人数,
y代表面试人数,若应聘的面试人数为60人,则该公司拟录用人数为(
)
(A)15
(B)40
(C)25
(D)130
4.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为(
)
(A)y=[]
(B)y=[]
(C)y=[]
(D)y=[]
二、填空题(每小题4分,共8分)
5.某不法商人将彩电先按原价提高40%,然后在广告上写上“大酬宾,八折优惠”,结果是每台彩电比原价多赚了270元,那么每台彩电原价是__________元.
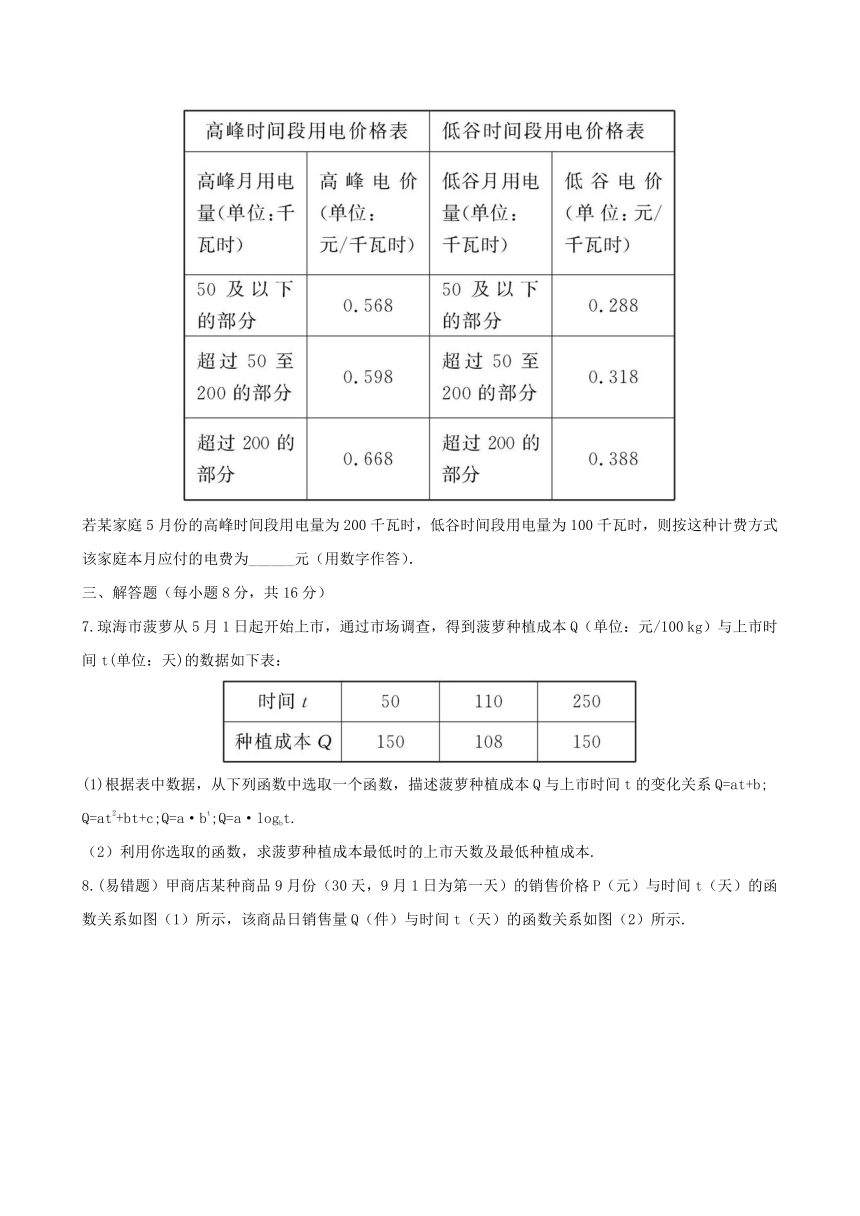
6.某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:
若某家庭5月份的高峰时间段用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为______元(用数字作答).
三、解答题(每小题8分,共16分)
7.琼海市菠萝从5月1日起开始上市,通过市场调查,得到菠萝种植成本Q(单位:元/100
kg)与上市时间t(单位:天)的数据如下表:
(1)根据表中数据,从下列函数中选取一个函数,描述菠萝种植成本Q与上市时间t的变化关系Q=at+b;
Q=at2+bt+c;Q=a·bt;Q=a·logbt.
(2)利用你选取的函数,求菠萝种植成本最低时的上市天数及最低种植成本.
8.(易错题)甲商店某种商品9月份(30天,9月1日为第一天)的销售价格P(元)与时间t(天)的函数关系如图(1)所示,该商品日销售量Q(件)与时间t(天)的函数关系如图(2)所示.
(1)写出:图(1)表示的销售价格与时间的函数关系式P=f(t),图(2)表示的日销售量与时间的函数关系式Q=g(t),及日销售金额M(元)与时间的函数关系M=h(t).
(2)乙商店销售同一种商品,在9月份采用另一种销售策略,日销售金额N(元)与时间t(天)之间的函数关系为N=-2t2-10t+2
750,比较9月份每天两商店销售金额的大小.
【挑战能力】
(10分)某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
(1)分别写出两种产品的收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大利益,其最大收益是多少万元?
答案解析
1.【解析】选D.
把点的坐标(1,1)(3,8)代入四个选项检验,可知只有D选项符合题意.
2.【解析】选C.假设经过x年,剩余的物质是原来的.由题意可知()x=.解得x=3.
3.【解析】选C.若4x=60,则x=15>10,不合题意;若2x+10=60,则x=25,满足题意;若1.5x=60,则x=40<100,不合题意.故拟录用人数为25人.
【举一反三】若应聘的面试人数为90人,其他条件不变,则该公司拟录用人数为(
)
(A)15
(B)40
(C)25
(D)130
【解析】选B.若4x=90,则x=22.5>10,不合题意;若2x+10=90,则x=40,满足题意;若1.5x=90,则x=60<100,不合题意.故拟录用人数为40人.
4.【解题指南】求解本题可抓住“当各班人数除以10的余数大于6时再增选一名代表”这一特征,并借助特殊值法求解.
【解析】选B.由题意,可用特殊值法求解,当x=17时,A选项错误,当x=16时,[]=2,[]=2,所以C,D选项错误,故选B.
【方法技巧】特殊值法解选择题的方法技巧
用特殊值(特殊数值、特殊图形、特殊位置、特殊情形等)代替题设普遍条件,得出特殊结论,对各个选项进行检验,从而作出正确的判断.常用的特殊值有特殊数值、特殊数列、特殊函数、特殊图形、特殊角、特殊位置等,注意:特殊值法只能否定选择项,不能肯定选择项.
当正确的选择对象在题设普遍条件下都成立的情况下,用特殊值(取得越简单越好)进行探求,从而清晰、快捷地得到正确的答案,即通过对特殊情况的研究来判断一般规律,是解答本类选择题的最佳策略.
5.【解析】设每台彩电原价为x元,依题意有80%·x(1+40%)-x=270.解得x=2
250.
答案:2
250
6.【解析】应付的电费应分两部分构成:
高峰部分为50×0.568+150×0.598;
低谷部分为50×0.288+50×0.318,
两部分之和为148.4.
答案:148.4
【变式训练】一辆汽车在某段路程中的行驶速度与时间的关系如图所示.
(1)图中阴影部分的面积等于_______;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2
004
km,试建立汽车行驶这段路程时汽车里程表读数S
km与时间t
h的函数解析式为______.
【解析】(1)阴影部分面积为:
50×1+80×1+90×1+75×1+65×1=360.
(2)根据图有:
S=
答案:(1)360
7.【解析】(1)由表中的数据知,当时间t变化时,种植成本并不是单调的,故只能选取Q=at2+bt+c,
即
解得:Q=.
(2)由(1)知Q=
=
(t-150)2+100.
当t=150天时,菠萝种植成本最低为Q=100元/100
kg.
8.【解析】(1)设价格函数是y=kt+b,过(0,15),(30,30),
则
∴f(t)=t+15(0≤t≤30,t∈N).
设销售量函数y=at+m,过(0,160),(30,40),
则
∴g(t)=-4t+160(0≤t≤30,t∈N).
则M=(t+15)(-4t+160)=-2t2+20t+2
400(0≤t≤30,t∈N).
(2)N=-2t2-10t+2
750(t∈N),M-N=30t-350.
当0≤t≤11时M-N<0,当12≤t≤30时M-N>0.
即前11天甲商店销售额少,以后乙商店均比甲商店少.
【挑战能力】
【解析】(1)设两种产品的收益与投资额的函数关系分别为f(x)=k1x,g(x)=k2,所以f(1)==k1,g(1)==k2,
即f(x)=x(x≥0),g(x)=(x≥0);
(2)设投资债券类产品x万元,则股票类投资为(20-x)万元,
依题意得:y=f(x)+g(20-x)=+(0≤x≤20),
令t=(0≤t≤),
则y=,
所以当t=2,即x=16万元时,收益最大,ymax=3万元.
实际问题的函数刻画
同步训练
(30分钟
50分)
一、选择题(每小题4分,共16分)
1.某种生物增长的数量y与时间x的关系如下表:
下面函数关系式中,能表达这种关系的是(
)
(A)y=x2-1
(B)y=2x-1
(C)y=2x-1
(D)y=1.5x2-2.5x+2
2.一种放射性物质不断变化为其他物质,每经过一年,剩余的物质为原来的,则经过多少年,剩余的物质是原来的
(
)
(A)5
(B)4
(C)3
(D)2
3.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为:
y=,其中,x代表拟录用人数,
y代表面试人数,若应聘的面试人数为60人,则该公司拟录用人数为(
)
(A)15
(B)40
(C)25
(D)130
4.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为(
)
(A)y=[]
(B)y=[]
(C)y=[]
(D)y=[]
二、填空题(每小题4分,共8分)
5.某不法商人将彩电先按原价提高40%,然后在广告上写上“大酬宾,八折优惠”,结果是每台彩电比原价多赚了270元,那么每台彩电原价是__________元.
6.某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:
若某家庭5月份的高峰时间段用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为______元(用数字作答).
三、解答题(每小题8分,共16分)
7.琼海市菠萝从5月1日起开始上市,通过市场调查,得到菠萝种植成本Q(单位:元/100
kg)与上市时间t(单位:天)的数据如下表:
(1)根据表中数据,从下列函数中选取一个函数,描述菠萝种植成本Q与上市时间t的变化关系Q=at+b;
Q=at2+bt+c;Q=a·bt;Q=a·logbt.
(2)利用你选取的函数,求菠萝种植成本最低时的上市天数及最低种植成本.
8.(易错题)甲商店某种商品9月份(30天,9月1日为第一天)的销售价格P(元)与时间t(天)的函数关系如图(1)所示,该商品日销售量Q(件)与时间t(天)的函数关系如图(2)所示.
(1)写出:图(1)表示的销售价格与时间的函数关系式P=f(t),图(2)表示的日销售量与时间的函数关系式Q=g(t),及日销售金额M(元)与时间的函数关系M=h(t).
(2)乙商店销售同一种商品,在9月份采用另一种销售策略,日销售金额N(元)与时间t(天)之间的函数关系为N=-2t2-10t+2
750,比较9月份每天两商店销售金额的大小.
【挑战能力】
(10分)某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
(1)分别写出两种产品的收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大利益,其最大收益是多少万元?
答案解析
1.【解析】选D.
把点的坐标(1,1)(3,8)代入四个选项检验,可知只有D选项符合题意.
2.【解析】选C.假设经过x年,剩余的物质是原来的.由题意可知()x=.解得x=3.
3.【解析】选C.若4x=60,则x=15>10,不合题意;若2x+10=60,则x=25,满足题意;若1.5x=60,则x=40<100,不合题意.故拟录用人数为25人.
【举一反三】若应聘的面试人数为90人,其他条件不变,则该公司拟录用人数为(
)
(A)15
(B)40
(C)25
(D)130
【解析】选B.若4x=90,则x=22.5>10,不合题意;若2x+10=90,则x=40,满足题意;若1.5x=90,则x=60<100,不合题意.故拟录用人数为40人.
4.【解题指南】求解本题可抓住“当各班人数除以10的余数大于6时再增选一名代表”这一特征,并借助特殊值法求解.
【解析】选B.由题意,可用特殊值法求解,当x=17时,A选项错误,当x=16时,[]=2,[]=2,所以C,D选项错误,故选B.
【方法技巧】特殊值法解选择题的方法技巧
用特殊值(特殊数值、特殊图形、特殊位置、特殊情形等)代替题设普遍条件,得出特殊结论,对各个选项进行检验,从而作出正确的判断.常用的特殊值有特殊数值、特殊数列、特殊函数、特殊图形、特殊角、特殊位置等,注意:特殊值法只能否定选择项,不能肯定选择项.
当正确的选择对象在题设普遍条件下都成立的情况下,用特殊值(取得越简单越好)进行探求,从而清晰、快捷地得到正确的答案,即通过对特殊情况的研究来判断一般规律,是解答本类选择题的最佳策略.
5.【解析】设每台彩电原价为x元,依题意有80%·x(1+40%)-x=270.解得x=2
250.
答案:2
250
6.【解析】应付的电费应分两部分构成:
高峰部分为50×0.568+150×0.598;
低谷部分为50×0.288+50×0.318,
两部分之和为148.4.
答案:148.4
【变式训练】一辆汽车在某段路程中的行驶速度与时间的关系如图所示.
(1)图中阴影部分的面积等于_______;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2
004
km,试建立汽车行驶这段路程时汽车里程表读数S
km与时间t
h的函数解析式为______.
【解析】(1)阴影部分面积为:
50×1+80×1+90×1+75×1+65×1=360.
(2)根据图有:
S=
答案:(1)360
7.【解析】(1)由表中的数据知,当时间t变化时,种植成本并不是单调的,故只能选取Q=at2+bt+c,
即
解得:Q=.
(2)由(1)知Q=
=
(t-150)2+100.
当t=150天时,菠萝种植成本最低为Q=100元/100
kg.
8.【解析】(1)设价格函数是y=kt+b,过(0,15),(30,30),
则
∴f(t)=t+15(0≤t≤30,t∈N).
设销售量函数y=at+m,过(0,160),(30,40),
则
∴g(t)=-4t+160(0≤t≤30,t∈N).
则M=(t+15)(-4t+160)=-2t2+20t+2
400(0≤t≤30,t∈N).
(2)N=-2t2-10t+2
750(t∈N),M-N=30t-350.
当0≤t≤11时M-N<0,当12≤t≤30时M-N>0.
即前11天甲商店销售额少,以后乙商店均比甲商店少.
【挑战能力】
【解析】(1)设两种产品的收益与投资额的函数关系分别为f(x)=k1x,g(x)=k2,所以f(1)==k1,g(1)==k2,
即f(x)=x(x≥0),g(x)=(x≥0);
(2)设投资债券类产品x万元,则股票类投资为(20-x)万元,
依题意得:y=f(x)+g(20-x)=+(0≤x≤20),
令t=(0≤t≤),
则y=,
所以当t=2,即x=16万元时,收益最大,ymax=3万元.
