4.2.3 函数建模案例 同步测试(含答案)
文档属性
| 名称 | 4.2.3 函数建模案例 同步测试(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 45.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-14 18:05:37 | ||
图片预览


文档简介
4.2.3
函数建模案例
同步测试
一、选择题
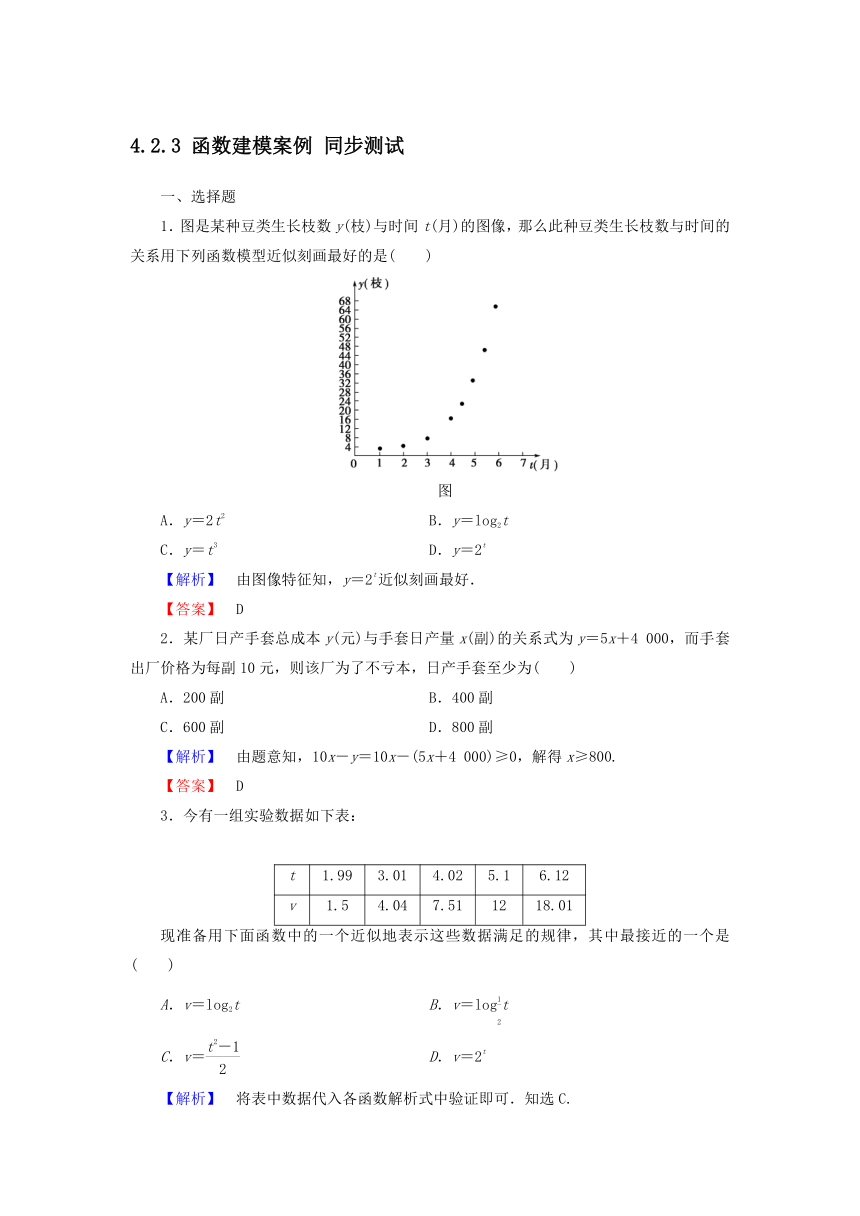
1.图是某种豆类生长枝数y(枝)与时间t(月)的图像,那么此种豆类生长枝数与时间的关系用下列函数模型近似刻画最好的是( )
图
A.y=2t2
B.y=log2t
C.y=t3
D.y=2t
【解析】 由图像特征知,y=2t近似刻画最好.
【答案】 D
2.某厂日产手套总成本y(元)与手套日产量x(副)的关系式为y=5x+4
000,而手套出厂价格为每副10元,则该厂为了不亏本,日产手套至少为( )
A.200副
B.400副
C.600副
D.800副
【解析】 由题意知,10x-y=10x-(5x+4
000)≥0,解得x≥800.
【答案】 D
3.今有一组实验数据如下表:
t
1.99
3.01
4.02
5.1
6.12
v
1.5
4.04
7.51
12
18.01
现准备用下面函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是( )
A.v=log2t
B.v=logt
C.v=
D.v=2t
【解析】 将表中数据代入各函数解析式中验证即可.知选C.
【答案】 C
4.我国为了加强对烟酒生产的宏观管理,除了应征税收外,还征收附加税.已知某种酒每瓶售价为70元,不收附加税时,每年大约销售100万瓶;若每销售100元国家要征附加税x元(叫做税率x%),则每年销售量将减少10x万瓶,如果要使每年在此项经营中所收取的附加税额不少于112万元,则x的最小值为( )
A.2
B.6
C.8
D.10
【解析】 依题意有(100-10x)×70×≥112.
∴2≤x≤8.
【答案】 A
5.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为:y=其中,x代表拟录用人数,y代表面试人数,若应聘的面试人数为60,则该公司拟录用人数为( )
A.15
B.40
C.25
D.130
【解析】 令y=60,
若4x=60,则x=15>10,不合题意;
若2x+10=60,则x=25,满足题意;
若1.5x=60,则x=40<100,不合题意.
故拟录用人数为25人.
【答案】 C
二、填空题
6.经市场调查,某商品的日销售量(单位:件)和价格(单位:元/件)均为时间t(单位:天)的函数.日销售量为f(t)=2t+100,价格为g(t)=t+4,则该种商品的日销售额S(单位:元)与时间t的函数关系式为S(t)=________.
【解析】 日销售额S=f(t)·g(t)=(2t+100)(t+4).
【答案】 (2t+100)(t+4)
7.将长度为1的铁丝分成两段,分别围成一个正方形和一个圆,要使正方形与圆的面积之和最小,正方形的周长应为________.
【解析】 设正方形的周长为x,则圆的周长为1-x,则
正方形与圆的面积和为S=()2+π·()2
=x2-x+(0<x<1),
∴x=-=时,S有最小值.
【答案】
8.国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4
000元的按超出800元部分的14%纳税;超过4
000元的按全稿酬的11.2%纳税.某人出版了一书共纳税420元,这个人的稿费为________元.
【解析】 设稿费为x元,纳税为y元,由题意可知
y=
∵此人纳税为420元,∴(x-800)×14%=420,
∴x=3
800.
【答案】 3
800
三、解答题
图4-2-3
9.某单位用木料制作如图4-2-3所示的框架,框架的下部是一组邻边长分别为x,y(单位:m)的矩形,上部是等腰直角三角形,要求框架的总面积为8
m2.
(1)写出y与x的函数关系式;
(2)写出用料l与x的函数关系式.
【解】 (1)由题意,得x2+xy=8,
所以y=-(0(2)由题意,得l=2x+2y+2(x)
=2x+x+2y=(+)x+,
所以l=(+)x+
(010.为应对国际金融危机对企业带来的不利影响,2011年底某企业实行裁员增效,已知现有员工200人,每人每年可创纯利润1万元,据评估,在生产条件不变的情况下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人(被裁员的员工)0.4万元生活费,并且企业正常运行所需人数不得少于现有员工的.设该企业裁员x人后纯收益为y万元.
(1)写出y关于x的函数关系式,并指出x的取值范围;
(2)问该企业裁员多少人,才能获得最大的经济效益?
【解】 (1)裁员x人后,企业员工数为(200-x)人,每人每年创纯利润(1+0.01x)万元,企业每年需付给下岗工人0.4x万元,
则y=(200-x)(1+0.01x)-0.4x=-0.01x2+0.6x+200.
∵200-x≥×200 x≤50,
∴x的取值范围为0(2)y=-0.01(x-30)2+209,
∵0∴当x=30时,y取得最大值209.
∴该企业应裁员30人,可获得年最大纯收益209万元.
11.某地区不同身高的未成年男性的体重平均值如下表:
身高/cm
60
70
80
90
100
110
体重/kg
6.13
7.90
9.99
12.15
15.02
17.50
身高/cm
120
130
140
150
160
170
体重/kg
20.92
26.86
31.11
38.85
47.25
55.05
(1)根据表中提供的数据,能否建立恰当的函数模型,使它能比较近似地反应这个地区未成年男性体重y(kg)与身高x(cm)的函数关系?若能,试写出这个函数模型的解析式;
(2)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为175
cm,体重为78
kg的未成年男性的体重是否正常?
【解】 (1)以身高为横坐标,体重为纵坐标,画出散点图,如图.根据点的分布特征,可考虑以y=a·bx作为刻画这个地区未成年男性的体重与身高关系的函数模型.
不妨取其中的两组数据(70,7.90),(160,47.25),
代入y=a·bx,得用计算器算得a≈2,b≈1.02.
这样,我们就得到一个函数模型:y=2×1.02x.
将已知数据代入上述函数解析式或作出上述函数的图像,可以发现这个函数模型与已知数据的拟合程度较好,这说明它能较好地反映这个地区未成年男性的体重与身高的关系.
(2)将x=175代入y=2×1.02x,得y=2×1.02175,由计算器可得y≈63.98.
由于78÷63.98≈1.22>1.2,所以该未成年男性偏胖.
函数建模案例
同步测试
一、选择题
1.图是某种豆类生长枝数y(枝)与时间t(月)的图像,那么此种豆类生长枝数与时间的关系用下列函数模型近似刻画最好的是( )
图
A.y=2t2
B.y=log2t
C.y=t3
D.y=2t
【解析】 由图像特征知,y=2t近似刻画最好.
【答案】 D
2.某厂日产手套总成本y(元)与手套日产量x(副)的关系式为y=5x+4
000,而手套出厂价格为每副10元,则该厂为了不亏本,日产手套至少为( )
A.200副
B.400副
C.600副
D.800副
【解析】 由题意知,10x-y=10x-(5x+4
000)≥0,解得x≥800.
【答案】 D
3.今有一组实验数据如下表:
t
1.99
3.01
4.02
5.1
6.12
v
1.5
4.04
7.51
12
18.01
现准备用下面函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是( )
A.v=log2t
B.v=logt
C.v=
D.v=2t
【解析】 将表中数据代入各函数解析式中验证即可.知选C.
【答案】 C
4.我国为了加强对烟酒生产的宏观管理,除了应征税收外,还征收附加税.已知某种酒每瓶售价为70元,不收附加税时,每年大约销售100万瓶;若每销售100元国家要征附加税x元(叫做税率x%),则每年销售量将减少10x万瓶,如果要使每年在此项经营中所收取的附加税额不少于112万元,则x的最小值为( )
A.2
B.6
C.8
D.10
【解析】 依题意有(100-10x)×70×≥112.
∴2≤x≤8.
【答案】 A
5.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为:y=其中,x代表拟录用人数,y代表面试人数,若应聘的面试人数为60,则该公司拟录用人数为( )
A.15
B.40
C.25
D.130
【解析】 令y=60,
若4x=60,则x=15>10,不合题意;
若2x+10=60,则x=25,满足题意;
若1.5x=60,则x=40<100,不合题意.
故拟录用人数为25人.
【答案】 C
二、填空题
6.经市场调查,某商品的日销售量(单位:件)和价格(单位:元/件)均为时间t(单位:天)的函数.日销售量为f(t)=2t+100,价格为g(t)=t+4,则该种商品的日销售额S(单位:元)与时间t的函数关系式为S(t)=________.
【解析】 日销售额S=f(t)·g(t)=(2t+100)(t+4).
【答案】 (2t+100)(t+4)
7.将长度为1的铁丝分成两段,分别围成一个正方形和一个圆,要使正方形与圆的面积之和最小,正方形的周长应为________.
【解析】 设正方形的周长为x,则圆的周长为1-x,则
正方形与圆的面积和为S=()2+π·()2
=x2-x+(0<x<1),
∴x=-=时,S有最小值.
【答案】
8.国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4
000元的按超出800元部分的14%纳税;超过4
000元的按全稿酬的11.2%纳税.某人出版了一书共纳税420元,这个人的稿费为________元.
【解析】 设稿费为x元,纳税为y元,由题意可知
y=
∵此人纳税为420元,∴(x-800)×14%=420,
∴x=3
800.
【答案】 3
800
三、解答题
图4-2-3
9.某单位用木料制作如图4-2-3所示的框架,框架的下部是一组邻边长分别为x,y(单位:m)的矩形,上部是等腰直角三角形,要求框架的总面积为8
m2.
(1)写出y与x的函数关系式;
(2)写出用料l与x的函数关系式.
【解】 (1)由题意,得x2+xy=8,
所以y=-(0
=2x+x+2y=(+)x+,
所以l=(+)x+
(0
(1)写出y关于x的函数关系式,并指出x的取值范围;
(2)问该企业裁员多少人,才能获得最大的经济效益?
【解】 (1)裁员x人后,企业员工数为(200-x)人,每人每年创纯利润(1+0.01x)万元,企业每年需付给下岗工人0.4x万元,
则y=(200-x)(1+0.01x)-0.4x=-0.01x2+0.6x+200.
∵200-x≥×200 x≤50,
∴x的取值范围为0
∵0
∴该企业应裁员30人,可获得年最大纯收益209万元.
11.某地区不同身高的未成年男性的体重平均值如下表:
身高/cm
60
70
80
90
100
110
体重/kg
6.13
7.90
9.99
12.15
15.02
17.50
身高/cm
120
130
140
150
160
170
体重/kg
20.92
26.86
31.11
38.85
47.25
55.05
(1)根据表中提供的数据,能否建立恰当的函数模型,使它能比较近似地反应这个地区未成年男性体重y(kg)与身高x(cm)的函数关系?若能,试写出这个函数模型的解析式;
(2)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为175
cm,体重为78
kg的未成年男性的体重是否正常?
【解】 (1)以身高为横坐标,体重为纵坐标,画出散点图,如图.根据点的分布特征,可考虑以y=a·bx作为刻画这个地区未成年男性的体重与身高关系的函数模型.
不妨取其中的两组数据(70,7.90),(160,47.25),
代入y=a·bx,得用计算器算得a≈2,b≈1.02.
这样,我们就得到一个函数模型:y=2×1.02x.
将已知数据代入上述函数解析式或作出上述函数的图像,可以发现这个函数模型与已知数据的拟合程度较好,这说明它能较好地反映这个地区未成年男性的体重与身高的关系.
(2)将x=175代入y=2×1.02x,得y=2×1.02175,由计算器可得y≈63.98.
由于78÷63.98≈1.22>1.2,所以该未成年男性偏胖.
