函数的最值与导数课件人教A版(选修1-1)
文档属性
| 名称 | 函数的最值与导数课件人教A版(选修1-1) |

|
|
| 格式 | rar | ||
| 文件大小 | 574.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-12 00:00:00 | ||
图片预览






文档简介
课件25张PPT。第三章 导数及其应用3.3.3 函数的最值与导数极值反映的是函数在某一点附近的局部
性质,而不是函数在整个定义域内的性质。但是我们往往更关心函数在某个区间上
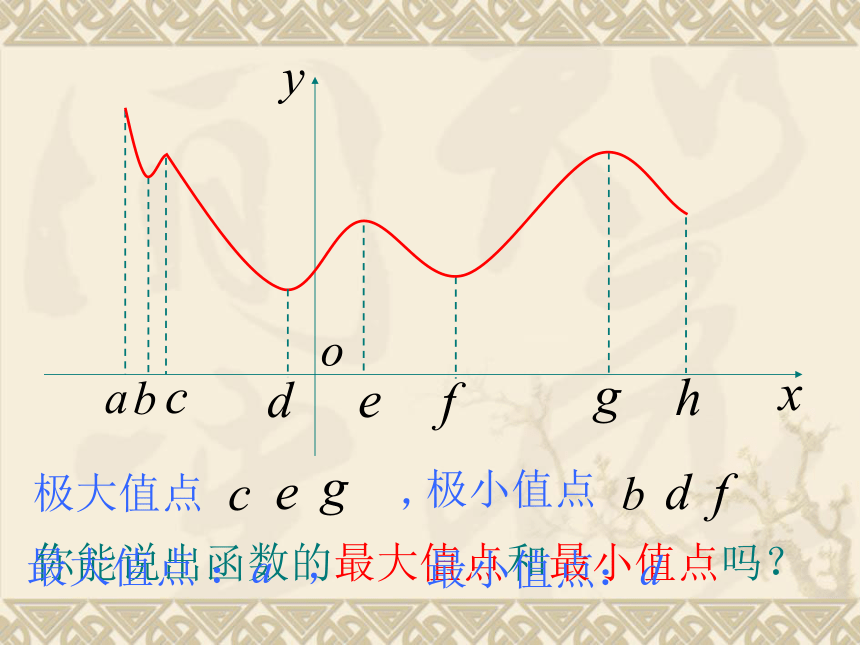
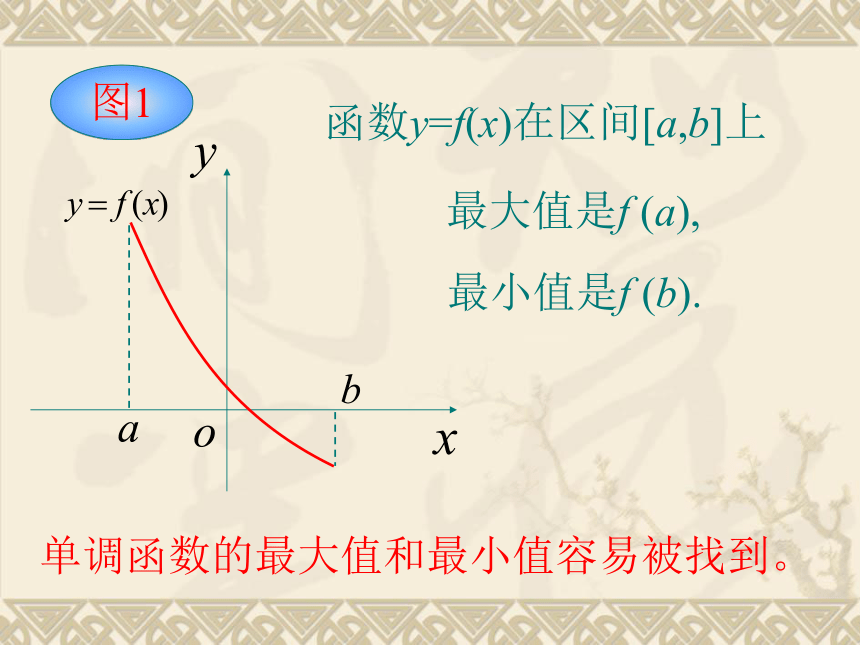
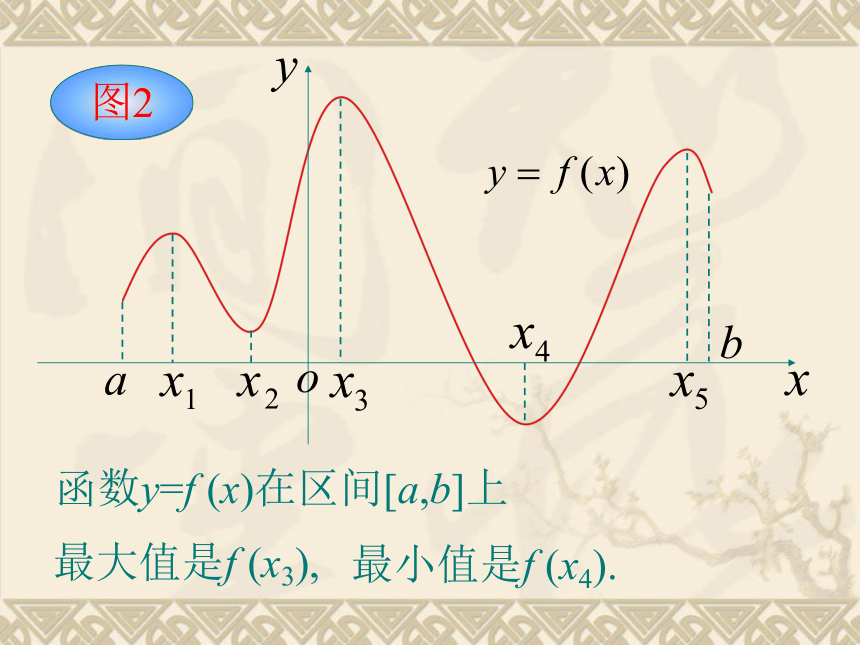
哪个值最大,哪个值最小。观察区间[a,b]上函数y=f (x)的图象,你能找出它的极大值点,极小值点吗?你能说出函数的最大值点和最小值点吗?最大值点 :a ,最小值点:d最小值是f (b).单调函数的最大值和最小值容易被找到。函数y=f(x)在区间[a,b]上最大值是f (a),图1最大值是f (x3),图2函数y=f (x)在区间[a,b]上最小值是f (x4).一般地,如果在区间[a,b]上函数y=f (x)
的图象是一条连续不断的曲线,那么
它必有最大值和最小值。怎样求函数y=f (x)在区间[a ,b]内的最大值
和最小值?思考只要把函数y=f (x)的所有极值连同端点
的函数值进行比较即可。例1、求函数f(x)=x3-12x+12在[0, 3]上的
最大值,最小值。例1、求函数f(x)=x3-12x+12在[0,3]上的
最大值,最小值。解:由上节课的例1知,在[0,3]上, 当x=2时, f(x)=x3-12x+12有极小值,并且极小值为f (2)=-4.又由于f (0)=12,f (3)=3,因此,函数 f(x)=x3-12x+12在[0, 3]上的
最大值为12,最小值为-4。①求函数y=f(x)在(a,b)内的极值
(极大值与极小值); ②将函数y=f(x)的各极值与f(a)、f(b)(即端点的函数值)作比较,其中最大的一个为最大值,最小的一个为最小值. 求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下练习1、求函数y=5-36x+3x2+4x3在区间
[-2,2]上的最大值与最小值。因为f(-2)=57, f(1.5)=-28.75, f(2)=-23所以函数的最大值为57,最小值为-28.75练习2、求函数f(x)=x3-3x2+6x-2在区间
[-1,1]上的最值。所以 f(x)在[-1,1]上是增函数,故当x=-1时,f(x)取得最小值-12;当x=1时,f(x)取得最大值2。例2、已知函数f(x)=-x3+3x2+9x+a;
(1)求f(x)的单调递减区间;
(2)若f(x)在区间[-2,2]上的最大值为20,
求它在该区间上的最小值。函数f(x)的单调递减区间为
(-∞,-1) ∪(3,+∞)(2) ∵f(-2)=8+12-18+a=2+af(2)=-8+12+18+a=22+a∴f(2)>f(-2)于是有22+a=20,解得a=-2∴f(x)=-x3+3x2+9x-2∴f(x)在[-1,2]上单调递增又由于f(x)在[-2,-1]上单调递减,即函数f(x)在区间[-2,2]上的最小值为-7。∴ f(2)和f(-1)分别是f(x)在区间[-2,2]上的
最大值和最小值。∴f(-1)=1+3-9-2=-7,例3、证明:当x>0时,x>ln(1+x)解:设f(x)=x-ln(1+x).即x>ln(1+x).又因为f(x)在x=0处连续,所以f(x)在x≥0上单调递增,从而当x>0时,有f(x)=x-ln(1+x)>f(0)=0练习3:当x>1时,证明不等式:显然f(x)在[1,+∞)上连续,且f(1)=0.例4、求证当x=1时,f(x)有极小值,这里也是最小值所以当x>0时,f(x) ≥f(1)=0小 结:①求函数y=f(x)在(a,b)内的极值
(极大值与极小值); ②将函数y=f(x)的各极值与f(a)、f(b)(即端点的函数值)作比较,其中最大的一个为最大值,最小的一个为最小值. 求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下再见
性质,而不是函数在整个定义域内的性质。但是我们往往更关心函数在某个区间上
哪个值最大,哪个值最小。观察区间[a,b]上函数y=f (x)的图象,你能找出它的极大值点,极小值点吗?你能说出函数的最大值点和最小值点吗?最大值点 :a ,最小值点:d最小值是f (b).单调函数的最大值和最小值容易被找到。函数y=f(x)在区间[a,b]上最大值是f (a),图1最大值是f (x3),图2函数y=f (x)在区间[a,b]上最小值是f (x4).一般地,如果在区间[a,b]上函数y=f (x)
的图象是一条连续不断的曲线,那么
它必有最大值和最小值。怎样求函数y=f (x)在区间[a ,b]内的最大值
和最小值?思考只要把函数y=f (x)的所有极值连同端点
的函数值进行比较即可。例1、求函数f(x)=x3-12x+12在[0, 3]上的
最大值,最小值。例1、求函数f(x)=x3-12x+12在[0,3]上的
最大值,最小值。解:由上节课的例1知,在[0,3]上, 当x=2时, f(x)=x3-12x+12有极小值,并且极小值为f (2)=-4.又由于f (0)=12,f (3)=3,因此,函数 f(x)=x3-12x+12在[0, 3]上的
最大值为12,最小值为-4。①求函数y=f(x)在(a,b)内的极值
(极大值与极小值); ②将函数y=f(x)的各极值与f(a)、f(b)(即端点的函数值)作比较,其中最大的一个为最大值,最小的一个为最小值. 求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下练习1、求函数y=5-36x+3x2+4x3在区间
[-2,2]上的最大值与最小值。因为f(-2)=57, f(1.5)=-28.75, f(2)=-23所以函数的最大值为57,最小值为-28.75练习2、求函数f(x)=x3-3x2+6x-2在区间
[-1,1]上的最值。所以 f(x)在[-1,1]上是增函数,故当x=-1时,f(x)取得最小值-12;当x=1时,f(x)取得最大值2。例2、已知函数f(x)=-x3+3x2+9x+a;
(1)求f(x)的单调递减区间;
(2)若f(x)在区间[-2,2]上的最大值为20,
求它在该区间上的最小值。函数f(x)的单调递减区间为
(-∞,-1) ∪(3,+∞)(2) ∵f(-2)=8+12-18+a=2+af(2)=-8+12+18+a=22+a∴f(2)>f(-2)于是有22+a=20,解得a=-2∴f(x)=-x3+3x2+9x-2∴f(x)在[-1,2]上单调递增又由于f(x)在[-2,-1]上单调递减,即函数f(x)在区间[-2,2]上的最小值为-7。∴ f(2)和f(-1)分别是f(x)在区间[-2,2]上的
最大值和最小值。∴f(-1)=1+3-9-2=-7,例3、证明:当x>0时,x>ln(1+x)解:设f(x)=x-ln(1+x).即x>ln(1+x).又因为f(x)在x=0处连续,所以f(x)在x≥0上单调递增,从而当x>0时,有f(x)=x-ln(1+x)>f(0)=0练习3:当x>1时,证明不等式:显然f(x)在[1,+∞)上连续,且f(1)=0.例4、求证当x=1时,f(x)有极小值,这里也是最小值所以当x>0时,f(x) ≥f(1)=0小 结:①求函数y=f(x)在(a,b)内的极值
(极大值与极小值); ②将函数y=f(x)的各极值与f(a)、f(b)(即端点的函数值)作比较,其中最大的一个为最大值,最小的一个为最小值. 求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下再见
