随机事件的概率
图片预览











文档简介
(共33张PPT)
昨夜西风凋碧树,独上高楼,望尽天涯路
衣带渐宽终不悔,为依销得人憔悴
众里寻它千百度,蓦然回首,那人却在等火阑珊处
问题1.你是彩民吗?你买的彩票一定能中奖吗?
事件一:
事件二:
木柴燃烧能产生热量吗?
观察下列事件:
明天,地球还会转动
事件三:
事件四:
猜猜看:王义夫下一枪会中十环吗?
煮熟的鸭子,跑了
事件五:
事件六:
扔一块硬币,要是能出现正面就好了。
在标准大气压下,且温度低于0℃时,这里的雪会融化吗?
这些事件发生与否,各有什么特点呢?
(2)“木柴燃烧,产生能量”
(4)“某人射击一次,中靶”
(5)“掷一枚硬币,出现正面”
(6)“在标准大气压下且温度低于0℃时,雪融化”
必然发生
必然发生
不可能发生
不可能发生
可能发生也可能不发生
可能发生也可能不发生
(1)无特殊情况,明天地球仍会转动
(3)煮熟的鸭子,跑了
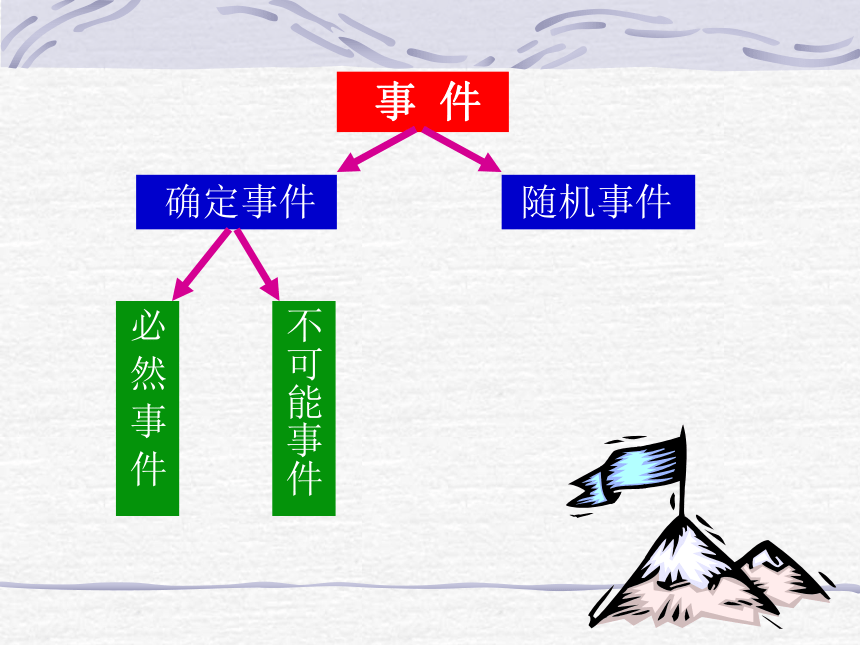
事 件
确定事件
随机事件
必 然 事 件
不可能事件
一、定义:
随机事件:
在条件S下可能发生也可能不发生的事件叫随机事件。
必然事件:
在条件S下必然要发生的事件叫必然事件。
不可能事件:
在条件S下不可能发生的事件叫不可能事件。
确定事件和随机事件统称为事件,一般用大写字母A,B,C…表示。
例1 指出下列事件是必然事件,不可能事件,还是随机事件:
(1)某地1月1日刮西北风;
(2)当x是实数,
;
(3)手电筒的电池没电,灯泡发亮;
(4)一个电影院某天的上座率超过50%。
随机事件
必然事件
不可能事件
随机事件
(5)打开电视机正在播放整点新闻
(6)在2010年的世界杯上,中国足球队以2:0战胜
巴西足球队
随机事件
随机事件
练习:
1、指出下列事件是必然事件、不可能事件、还是 随机事件?
(1)如果a,b都是实数,那么a+b=b+a;
(2)从分别标有号数1,2,3,4,5,6,7,8,9,10的10张号签中任取一张,得到4号签;
(3)没有水份,种籽发芽;
(4)某电话总机在60秒内接到至少15次呼唤;
(5)在标准大气压下,水的温度达到50℃,沸腾;
(6)同性电荷,相互排斥。
必然
随机
不可能
随机
必然
不可能
练习:
2、请你列举一些你了解的必然事件、不可能事件、随机事件。
二、试验及事件的概率
问:
随机事件的“可能发生也可能不发生”是不是没有任何规律地随意发生呢?
想一想?
让我们来做一个试验:
试验:把一枚硬币抛多次,观察其出现的结果,并记录各结果出现的频数,然后计算各频率。
同学们按课本P109的五个步骤做实验,并填写相应表格。
根据实验分别回答下列问题:
(1)在实验中出现了几种实验结果?还有其它实验结果吗?
(2)一次试验中的一个实验结果固定吗?有无规律?
(3)这些实验结果出现的频率有何关系?
(4)如果允许你做大量重复试验,你认为结果又如何呢?
实验中只出现两种结果,没有其它结果,每一次试验的结果不固定,但只是“正面”、“反面”两种中的一种,且它们出现的比例均接近于0.5,但不相等。
通过这么多的实验,我们可以发觉:
一、事件A的频数:
在相同的条件S下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现nA的次数为事件A出现的频数(frequency)。
二、事件A的频率:
称事件A出现的比例 为事件A出现的频率(relative frequency)。
思考: 频率的取值范围是什么?
[0,1]
实例 将一枚硬币抛掷 5 次、50 次、500 次, 各做
7 遍, 观察正面出现的次数及频率.
试验
序号
1 2 3 4 5 6 7
2
3
1 5 1 2 4
22
25
21
25
24
18
27
251
249
256
247
251
262
258
0.4
0.6
0.2
1.0
0.2
0.4
0.8
0.44
0.50
0.42
0.48
0.36
0.54
0.502
0.498
0.512
0.494
0.524
0.516
0.50
0.502
波动最小
随n的增大, 频率 f 呈现出稳定性
三、事件A的概率:
注:
事件A的概率:
(2)0≤P(A)≤1 不可能事件的概率为0,必然事件为1,随机事件的概率大于0而小于1。
一般地,在大量重复进行同一试验时,事件A发生的频率 总是接近于某个常数,在它附近摆动。这个常数叫做事件A的概率,记作P(A)。
(1)频率 总在P(A)附近摆动,当n越
大时,摆动幅度越小。
思考:频率与概率的有什么区别和联系
① 频率是随机的,在试验之前不能确定;
② 概率是一个确定的数,与每次试验无关;
①随着试验次数的增加,频率会越来越接近概率;
②频率是概率的近似值,概率是用来度量事
件发生可能性的大小.
区别:
联系:
练习:
1、下列事件:
(1)口袋里有伍角、壹角、壹元的硬币若干枚,随机地摸出一枚是壹角。
(2)在标准大气压下,水在90℃沸腾。
(3)射击运动员射击一次命中10环。
(4)同时掷两颗骰子,出现的点数之和不超过12。
其中是随机事件的有 ( )
A、 (1) B、(1)(2) C、(1)(3) D、(2)(4)
C
2、下列事件:
(1)a,b∈R且a(2)抛一石块,石块飞出地球。
(3)掷一枚硬币,正面向上。
(4)掷一颗骰子出现点8。
其中是不可能事件的是 ( )
A、(1)(2) B、(2)(3) C、(2)(4) D、(1)(4)
C
3、随机事件在n次试验中发生了m次,则( )
(A) 0<m<n (B) 0<n<m
(C) 0≤m≤n (D) 0≤n≤m
C
4、某射手在同一条件下进行射击,结果如下:
射击次数n 10 20 50 100 200 500
击中靶心的次数 m 8 19 44 92 178 455
击中靶心的频率m/n
(1)计算表中击中靶心的各个频率;
(2)这个射手射击一次,击中靶心的概率约为多少?
0.8
0.95
0.88
0.92
0.89
0.91
5、一个地区从某年起几年之内的新生儿数及其中的男婴数如下:
时间范围 1年内 2年内 3年内 4年内
新生婴儿数 5544 9607 13520 17190
男婴数 2883 4970 6994 8892
男婴出生频率
(1)填写上表中的男婴出生频率(如果用计算器计算,结果保留到小数点后第3位);
(2)这一地区男婴出生的概率约为多少?
0.520
0.517
0.517
0.517
课堂小结:
1、本节课需掌握的知识:
①了解必然事件,不可能事件,随机事件的概念;
② 理解频数、频率的意义。
③理解随机事件的发生在大量重复试验下,呈现规律性,它的频率接近一个常数。
2.频率与概率的区别和联系
1651年,法国一位贵族梅累向法国数学家、物理学家帕斯卡提出了一个十分有趣的 “分赌注”问题.
问题是这样的,一次梅累和赌友掷骰子,各押赌注32个金币.双方约定,梅累如果先掷出三次6点,或者赌友先掷三次4点,就算赢了对方.赌博进行了一段时间,梅累已经两次掷出6点,赌友已经一次掷出4点.这时候梅累接到通知,要他马上陪同国王接见外宾,赌博只好中断了.请问:两个人应该怎样分这64个金币才算合理呢
故事阅读
赌友说,他要再碰上两次4点,或梅累要再
碰上一次6点就算赢,所以他有权分得梅累
的一半,即梅累分64个金币的 ,自己分
64 个金币的 .
梅累争辩说,不对,即使下一次赌友掷出了4
点,他还可以得到 ,即32个金币;再加上
下一次他还有一半希望得到16个金币,所以
他应该分得64个金币的 ,赌友只能分得64
个金币的 .两人到底谁说得对呢
帕斯卡是17世纪有名的“神童”数学家。 可是,梅累提出的“分赌注”的问题,却把他难住了.他苦苦思考了两三年,到1654年才算有了点眉目,于是写信给他的好友费马,两人讨论结果,取得了一致的意见:梅累的分法是对的,他应得64个金币的四分之三,赌友应得64金币的四分之一。这时有位荷兰的数学家惠更斯在巴黎听到这件新闻,也参加了他们的讨论.讨论结果,惠更斯把它写成一本书叫做《论赌博中的计算》(1657年),这就是概率论最早的一部著作. 概率论现在已经成了数学的一个重要分支,在科学技术各领域里有着十分广泛的应用.
以经典的生日聚会为例子,以1年365天计,你如果肯定在某人群中至少要有两人生日相同,那么需要多少人?
大家不难得到结果,366人,只要人数超过365人,必然会有人生日相同。
现在请同学们想一下,如果一个班有60个人,他们中间至少有两人生日相同的概率是多少?
概率的应用:
你可能想,大概20%~30%,错!有90%的可能。
人数 至少有两人生日相同的概率
10 0.12
20 0.41
23 0.51
30 0.70
57 0.90
366 1.0
从上表可以看出,要有100%把握确认至少有两人生日相同需要366人,而有90%把握认为至少有两人生日相同只需要57人。大家可能奇怪,怎么会有这样的结果,通过本章的学习,同学们将对其有进一步的了解。
昨夜西风凋碧树,独上高楼,望尽天涯路
衣带渐宽终不悔,为依销得人憔悴
众里寻它千百度,蓦然回首,那人却在等火阑珊处
问题1.你是彩民吗?你买的彩票一定能中奖吗?
事件一:
事件二:
木柴燃烧能产生热量吗?
观察下列事件:
明天,地球还会转动
事件三:
事件四:
猜猜看:王义夫下一枪会中十环吗?
煮熟的鸭子,跑了
事件五:
事件六:
扔一块硬币,要是能出现正面就好了。
在标准大气压下,且温度低于0℃时,这里的雪会融化吗?
这些事件发生与否,各有什么特点呢?
(2)“木柴燃烧,产生能量”
(4)“某人射击一次,中靶”
(5)“掷一枚硬币,出现正面”
(6)“在标准大气压下且温度低于0℃时,雪融化”
必然发生
必然发生
不可能发生
不可能发生
可能发生也可能不发生
可能发生也可能不发生
(1)无特殊情况,明天地球仍会转动
(3)煮熟的鸭子,跑了
事 件
确定事件
随机事件
必 然 事 件
不可能事件
一、定义:
随机事件:
在条件S下可能发生也可能不发生的事件叫随机事件。
必然事件:
在条件S下必然要发生的事件叫必然事件。
不可能事件:
在条件S下不可能发生的事件叫不可能事件。
确定事件和随机事件统称为事件,一般用大写字母A,B,C…表示。
例1 指出下列事件是必然事件,不可能事件,还是随机事件:
(1)某地1月1日刮西北风;
(2)当x是实数,
;
(3)手电筒的电池没电,灯泡发亮;
(4)一个电影院某天的上座率超过50%。
随机事件
必然事件
不可能事件
随机事件
(5)打开电视机正在播放整点新闻
(6)在2010年的世界杯上,中国足球队以2:0战胜
巴西足球队
随机事件
随机事件
练习:
1、指出下列事件是必然事件、不可能事件、还是 随机事件?
(1)如果a,b都是实数,那么a+b=b+a;
(2)从分别标有号数1,2,3,4,5,6,7,8,9,10的10张号签中任取一张,得到4号签;
(3)没有水份,种籽发芽;
(4)某电话总机在60秒内接到至少15次呼唤;
(5)在标准大气压下,水的温度达到50℃,沸腾;
(6)同性电荷,相互排斥。
必然
随机
不可能
随机
必然
不可能
练习:
2、请你列举一些你了解的必然事件、不可能事件、随机事件。
二、试验及事件的概率
问:
随机事件的“可能发生也可能不发生”是不是没有任何规律地随意发生呢?
想一想?
让我们来做一个试验:
试验:把一枚硬币抛多次,观察其出现的结果,并记录各结果出现的频数,然后计算各频率。
同学们按课本P109的五个步骤做实验,并填写相应表格。
根据实验分别回答下列问题:
(1)在实验中出现了几种实验结果?还有其它实验结果吗?
(2)一次试验中的一个实验结果固定吗?有无规律?
(3)这些实验结果出现的频率有何关系?
(4)如果允许你做大量重复试验,你认为结果又如何呢?
实验中只出现两种结果,没有其它结果,每一次试验的结果不固定,但只是“正面”、“反面”两种中的一种,且它们出现的比例均接近于0.5,但不相等。
通过这么多的实验,我们可以发觉:
一、事件A的频数:
在相同的条件S下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现nA的次数为事件A出现的频数(frequency)。
二、事件A的频率:
称事件A出现的比例 为事件A出现的频率(relative frequency)。
思考: 频率的取值范围是什么?
[0,1]
实例 将一枚硬币抛掷 5 次、50 次、500 次, 各做
7 遍, 观察正面出现的次数及频率.
试验
序号
1 2 3 4 5 6 7
2
3
1 5 1 2 4
22
25
21
25
24
18
27
251
249
256
247
251
262
258
0.4
0.6
0.2
1.0
0.2
0.4
0.8
0.44
0.50
0.42
0.48
0.36
0.54
0.502
0.498
0.512
0.494
0.524
0.516
0.50
0.502
波动最小
随n的增大, 频率 f 呈现出稳定性
三、事件A的概率:
注:
事件A的概率:
(2)0≤P(A)≤1 不可能事件的概率为0,必然事件为1,随机事件的概率大于0而小于1。
一般地,在大量重复进行同一试验时,事件A发生的频率 总是接近于某个常数,在它附近摆动。这个常数叫做事件A的概率,记作P(A)。
(1)频率 总在P(A)附近摆动,当n越
大时,摆动幅度越小。
思考:频率与概率的有什么区别和联系
① 频率是随机的,在试验之前不能确定;
② 概率是一个确定的数,与每次试验无关;
①随着试验次数的增加,频率会越来越接近概率;
②频率是概率的近似值,概率是用来度量事
件发生可能性的大小.
区别:
联系:
练习:
1、下列事件:
(1)口袋里有伍角、壹角、壹元的硬币若干枚,随机地摸出一枚是壹角。
(2)在标准大气压下,水在90℃沸腾。
(3)射击运动员射击一次命中10环。
(4)同时掷两颗骰子,出现的点数之和不超过12。
其中是随机事件的有 ( )
A、 (1) B、(1)(2) C、(1)(3) D、(2)(4)
C
2、下列事件:
(1)a,b∈R且a
(3)掷一枚硬币,正面向上。
(4)掷一颗骰子出现点8。
其中是不可能事件的是 ( )
A、(1)(2) B、(2)(3) C、(2)(4) D、(1)(4)
C
3、随机事件在n次试验中发生了m次,则( )
(A) 0<m<n (B) 0<n<m
(C) 0≤m≤n (D) 0≤n≤m
C
4、某射手在同一条件下进行射击,结果如下:
射击次数n 10 20 50 100 200 500
击中靶心的次数 m 8 19 44 92 178 455
击中靶心的频率m/n
(1)计算表中击中靶心的各个频率;
(2)这个射手射击一次,击中靶心的概率约为多少?
0.8
0.95
0.88
0.92
0.89
0.91
5、一个地区从某年起几年之内的新生儿数及其中的男婴数如下:
时间范围 1年内 2年内 3年内 4年内
新生婴儿数 5544 9607 13520 17190
男婴数 2883 4970 6994 8892
男婴出生频率
(1)填写上表中的男婴出生频率(如果用计算器计算,结果保留到小数点后第3位);
(2)这一地区男婴出生的概率约为多少?
0.520
0.517
0.517
0.517
课堂小结:
1、本节课需掌握的知识:
①了解必然事件,不可能事件,随机事件的概念;
② 理解频数、频率的意义。
③理解随机事件的发生在大量重复试验下,呈现规律性,它的频率接近一个常数。
2.频率与概率的区别和联系
1651年,法国一位贵族梅累向法国数学家、物理学家帕斯卡提出了一个十分有趣的 “分赌注”问题.
问题是这样的,一次梅累和赌友掷骰子,各押赌注32个金币.双方约定,梅累如果先掷出三次6点,或者赌友先掷三次4点,就算赢了对方.赌博进行了一段时间,梅累已经两次掷出6点,赌友已经一次掷出4点.这时候梅累接到通知,要他马上陪同国王接见外宾,赌博只好中断了.请问:两个人应该怎样分这64个金币才算合理呢
故事阅读
赌友说,他要再碰上两次4点,或梅累要再
碰上一次6点就算赢,所以他有权分得梅累
的一半,即梅累分64个金币的 ,自己分
64 个金币的 .
梅累争辩说,不对,即使下一次赌友掷出了4
点,他还可以得到 ,即32个金币;再加上
下一次他还有一半希望得到16个金币,所以
他应该分得64个金币的 ,赌友只能分得64
个金币的 .两人到底谁说得对呢
帕斯卡是17世纪有名的“神童”数学家。 可是,梅累提出的“分赌注”的问题,却把他难住了.他苦苦思考了两三年,到1654年才算有了点眉目,于是写信给他的好友费马,两人讨论结果,取得了一致的意见:梅累的分法是对的,他应得64个金币的四分之三,赌友应得64金币的四分之一。这时有位荷兰的数学家惠更斯在巴黎听到这件新闻,也参加了他们的讨论.讨论结果,惠更斯把它写成一本书叫做《论赌博中的计算》(1657年),这就是概率论最早的一部著作. 概率论现在已经成了数学的一个重要分支,在科学技术各领域里有着十分广泛的应用.
以经典的生日聚会为例子,以1年365天计,你如果肯定在某人群中至少要有两人生日相同,那么需要多少人?
大家不难得到结果,366人,只要人数超过365人,必然会有人生日相同。
现在请同学们想一下,如果一个班有60个人,他们中间至少有两人生日相同的概率是多少?
概率的应用:
你可能想,大概20%~30%,错!有90%的可能。
人数 至少有两人生日相同的概率
10 0.12
20 0.41
23 0.51
30 0.70
57 0.90
366 1.0
从上表可以看出,要有100%把握确认至少有两人生日相同需要366人,而有90%把握认为至少有两人生日相同只需要57人。大家可能奇怪,怎么会有这样的结果,通过本章的学习,同学们将对其有进一步的了解。
