1.3 统计图表 学案4(含答案)
图片预览


文档简介
1.3
统计图表
学案
1.通过实例初步体会分布的意义和作用.
2.在表示数据的过程中,复习几种统计图表(包括条形、扇形、折线统计图),学习茎叶图,体会它们各自的特点和用途.
3.能根据问题的需要选择合适的统计图表,并能用自己的方式进行表示.
统计图表
统计图表是表达和分析________的重要工具,它不仅可以帮助我们从数据中获取有用的信息,还可以帮助我们直观、准确地理解相应的________.统计图表有:________统计图、________统计图、________统计图、茎叶图.
利用科学抽样方法收集了样本数据后,下一步要做的工作就是分析和处理数据,其中较理想的方法是将所得数据进行适当的整理、分析,并转化为直观的图形形式表现出来,以便从中获取相应的信息,帮助我们制定恰当的决策.
1.条形统计图是用____________表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按照一定的顺序排列起来.其特点是便于看出和比较各种数量的多少,即条形统计图能清楚地表示出每个项目的具体__________.
【做一做1】如图所示是某校八年级学生到校方式的条形统计图,根据图形可得出骑自行车人数占八年级学生总人数的( ).
A.20%
B.30%
C.50%
D.60%
2.扇形统计图中,用圆面积代表________,圆面中的各个扇形分别代表总体中的不同部分,扇形面积的大小反映____________________.扇形统计图可以很清楚地表示各部分数量同总数之间的关系,即扇形统计图能清楚地表示出各部分在总体中所占的__________.
【做一做2】如图为某校高三(1)班的男女比例图表,已知该班共有学生55人,则该班男生比女生约多( ).
A.13人
B.21人
C.24人
D.34人
3.折线统计图是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连结起来.折线统计图不但可以表示出__________,而且能够清楚地表示__________,即折线统计图能够清晰地反映数据的________情况.
【做一做3】如图是某市5月1日至5月7日每天最高、最低气温的折线统计图,在这7天中,日温差最大的一天是( ).
A.5月1日
B.5月2日
C.5月3日
D.5月5日
4.茎叶图.
(1)制作方法:将所有两位数的十位数字作为______,个位数字作为______,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶可以按从大到小(或从小到大)的顺序同行列出(也可以没有大小顺序).
(2)优点:一是茎叶图上没有________的损失,所有的原始数据都可以从茎叶图中得到;二是茎叶图可以随时________,方便表示与比较.
缺点:当数据量很大或有多组数据时,茎叶图就不那么直观、清晰了.
【做一做4】如图表示8位销售员一个月销售商品数量的茎叶图,则销售数据分别为________________(单位:百件).
如何选择统计图表统计所收集到的数据?
剖析:在统计过程中收集到的数据量较多时,在用统计图表示之前,一般需要先将数据按一定的方式进行整理.在此基础上,再根据不同的需要选择适当的统计图进行表示.
如果只需大致判断一些数据的分布规律,了解数据中各元素所占比例的大小情况可以使用扇形统计图.例如统计一个农村种植的各种农作物的比例.
如果需要根据图表了解各个数据所占的频率可以使用条形统计图.例如统计一批产品中优等品所占频率.
如果要了解数据的增减情况可以采用折线图.例如统计一个人考试成绩变化情况.
如果要了解数据的全部信息可以使用茎叶图.例如篮球比赛的记分.
因此要选择恰当的统计图表直观表达统计的数据,必须把各种统计图表的特点和问题中的需要结合起来,确定选择哪种统计图表.
题型一
条形统计图的应用
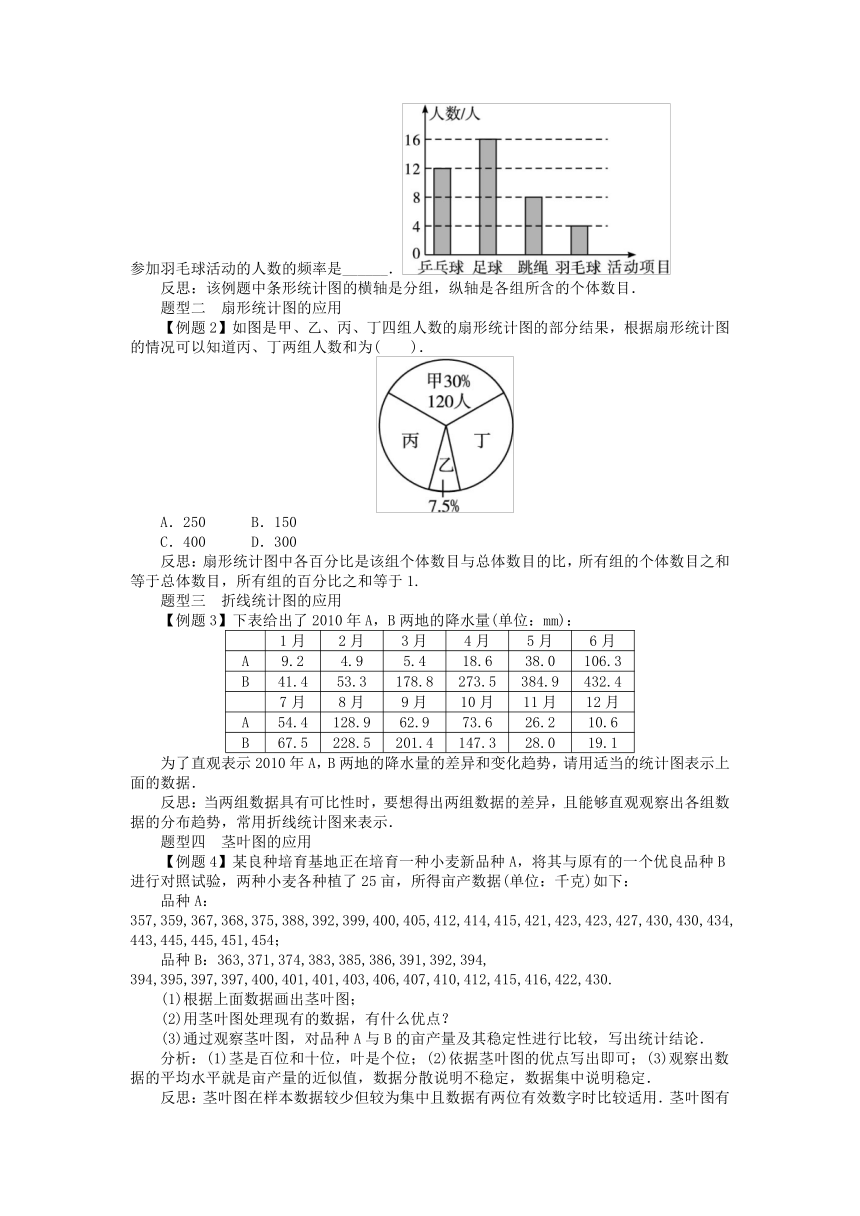
【例题1】某班计划开展一些课外活动,全班有40名学生报名参加,他们就乒乓球、足球、跳绳、羽毛球等4项活动的参加人数做了统计,绘制了条形统计图(如图所示),那么参加羽毛球活动的人数的频率是______.
反思:该例题中条形统计图的横轴是分组,纵轴是各组所含的个体数目.
题型二
扇形统计图的应用
【例题2】如图是甲、乙、丙、丁四组人数的扇形统计图的部分结果,根据扇形统计图的情况可以知道丙、丁两组人数和为( ).
A.250
B.150
C.400
D.300
反思:扇形统计图中各百分比是该组个体数目与总体数目的比,所有组的个体数目之和等于总体数目,所有组的百分比之和等于1.
题型三
折线统计图的应用
【例题3】下表给出了2010年A,B两地的降水量(单位:mm):
1月
2月
3月
4月
5月
6月
A
9.2
4.9
5.4
18.6
38.0
106.3
B
41.4
53.3
178.8
273.5
384.9
432.4
7月
8月
9月
10月
11月
12月
A
54.4
128.9
62.9
73.6
26.2
10.6
B
67.5
228.5
201.4
147.3
28.0
19.1
为了直观表示2010年A,B两地的降水量的差异和变化趋势,请用适当的统计图表示上面的数据.
反思:当两组数据具有可比性时,要想得出两组数据的差异,且能够直观观察出各组数据的分布趋势,常用折线统计图来表示.
题型四
茎叶图的应用
【例题4】某良种培育基地正在培育一种小麦新品种A,将其与原有的一个优良品种B进行对照试验,两种小麦各种植了25亩,所得亩产数据(单位:千克)如下:
品种A:357,359,367,368,375,388,392,399,400,405,412,414,415,421,423,423,427,430,430,434,443,445,445,451,454;
品种B:363,371,374,383,385,386,391,392,394,
394,395,397,397,400,401,401,403,406,407,410,412,415,416,422,430.
(1)根据上面数据画出茎叶图;
(2)用茎叶图处理现有的数据,有什么优点?
(3)通过观察茎叶图,对品种A与B的亩产量及其稳定性进行比较,写出统计结论.
分析:(1)茎是百位和十位,叶是个位;(2)依据茎叶图的优点写出即可;(3)观察出数据的平均水平就是亩产量的近似值,数据分散说明不稳定,数据集中说明稳定.
反思:茎叶图在样本数据较少但较为集中且数据有两位有效数字时比较适用.茎叶图有两个突出的优点,一是统计图上没有原始信息的损失,所有的数据信息都可以从茎叶图中得到;二是茎叶图可以在比赛时随时记录,方便记录和表示.
1当收集到的数据量很大或有多组数据时,需要比较各种数量的多少,用哪种统计图较合适( ).
A.茎叶图
B.条形统计图
C.折线统计图
D.扇形统计图
2如图是2009年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶图,则最低分和最高分分别为( ).
A.79,93
B.84,87
C.48,78
D.39,97
3某班学生在课外活动中参加文娱、美术、体育小组的人数之比为3∶1∶6,则在扇形统计图中表示参加体育小组人数的扇形圆心角是( ).
A.108°
B.216°
C.60°
D.36°
4甲、乙两个班级各随机选出15名同学进行测验,成绩的茎叶图如图所示,则甲班、乙班的最高成绩各是________,从图中看,________班的平均成绩较高.
5某地农村某户农民年收入如下(单位:元):
土地收入
打工收入
养殖收入
其他收入
4
320
3
600
2
357
843
请用不同的统计图来表示上面的数据.
答案:
基础知识·梳理
数据 结果 条形 扇形 折线
1.一个单位长度 数目
【做一做1】B
2.总体 部分占总体的百分比的大小 百分比
【做一做2】A
3.数量的多少 数量增减变化的情况 变化
【做一做3】D
4.(1)茎 叶 (2)信息 记录
【做一做4】45,45,52,56,57,58,60,63 由茎叶图可知销售数据都是两位数,分别为45,45,52,56,57,58,60,63.
典型例题·领悟
【例题1】0.1 参加羽毛球活动的人数是4,则频率为=0.1.
【例题2】A 甲组人数是120,占30%,则总人数是=400.则乙组人数是400×7.5%=30,则丙、丁两组人数和为400-120-30=250.
【例题3】解:用折线统计图表示题中的数据,如图.
其中虚线为B地降水量,实线为A地降水量.
【例题4】解:(1)茎叶图如图所示.
(2)用茎叶图处理现有的数据不仅可以看出数据的分布状况,而且可以看出每组中的具体数据.
(3)通过观察茎叶图,可以发现品种A的产量在420千克以上的亩数比品种B多10亩,而且品种A的产量在390千克以下的亩数与品种B一样多,由此可知,品种A的平均亩产量比品种B的平均亩产量高.但品种A的亩产量不够稳定,而品种B的亩产量比较集中,所以品种B的亩产量比较稳定.
随堂练习·巩固
1.
B 由于需要比较各种数量的多少,并且收集到的数据量很大或有多组数据,符合条形统计图的特点.
2.A
3.B 参加体育小组人数占总人数的×100%=60%,则扇形圆心角是360°×60%=216°.
4.96,92 乙
5.分析:题意的要求是将此四个数据用统计图表示出来,可利用条形统计图、折线统计图、扇形统计图来表示.
解:用条形统计图表示,如图所示.
用折线统计图表示,如图所示.
用扇形统计图表示,如图所示.
统计图表
学案
1.通过实例初步体会分布的意义和作用.
2.在表示数据的过程中,复习几种统计图表(包括条形、扇形、折线统计图),学习茎叶图,体会它们各自的特点和用途.
3.能根据问题的需要选择合适的统计图表,并能用自己的方式进行表示.
统计图表
统计图表是表达和分析________的重要工具,它不仅可以帮助我们从数据中获取有用的信息,还可以帮助我们直观、准确地理解相应的________.统计图表有:________统计图、________统计图、________统计图、茎叶图.
利用科学抽样方法收集了样本数据后,下一步要做的工作就是分析和处理数据,其中较理想的方法是将所得数据进行适当的整理、分析,并转化为直观的图形形式表现出来,以便从中获取相应的信息,帮助我们制定恰当的决策.
1.条形统计图是用____________表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按照一定的顺序排列起来.其特点是便于看出和比较各种数量的多少,即条形统计图能清楚地表示出每个项目的具体__________.
【做一做1】如图所示是某校八年级学生到校方式的条形统计图,根据图形可得出骑自行车人数占八年级学生总人数的( ).
A.20%
B.30%
C.50%
D.60%
2.扇形统计图中,用圆面积代表________,圆面中的各个扇形分别代表总体中的不同部分,扇形面积的大小反映____________________.扇形统计图可以很清楚地表示各部分数量同总数之间的关系,即扇形统计图能清楚地表示出各部分在总体中所占的__________.
【做一做2】如图为某校高三(1)班的男女比例图表,已知该班共有学生55人,则该班男生比女生约多( ).
A.13人
B.21人
C.24人
D.34人
3.折线统计图是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连结起来.折线统计图不但可以表示出__________,而且能够清楚地表示__________,即折线统计图能够清晰地反映数据的________情况.
【做一做3】如图是某市5月1日至5月7日每天最高、最低气温的折线统计图,在这7天中,日温差最大的一天是( ).
A.5月1日
B.5月2日
C.5月3日
D.5月5日
4.茎叶图.
(1)制作方法:将所有两位数的十位数字作为______,个位数字作为______,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶可以按从大到小(或从小到大)的顺序同行列出(也可以没有大小顺序).
(2)优点:一是茎叶图上没有________的损失,所有的原始数据都可以从茎叶图中得到;二是茎叶图可以随时________,方便表示与比较.
缺点:当数据量很大或有多组数据时,茎叶图就不那么直观、清晰了.
【做一做4】如图表示8位销售员一个月销售商品数量的茎叶图,则销售数据分别为________________(单位:百件).
如何选择统计图表统计所收集到的数据?
剖析:在统计过程中收集到的数据量较多时,在用统计图表示之前,一般需要先将数据按一定的方式进行整理.在此基础上,再根据不同的需要选择适当的统计图进行表示.
如果只需大致判断一些数据的分布规律,了解数据中各元素所占比例的大小情况可以使用扇形统计图.例如统计一个农村种植的各种农作物的比例.
如果需要根据图表了解各个数据所占的频率可以使用条形统计图.例如统计一批产品中优等品所占频率.
如果要了解数据的增减情况可以采用折线图.例如统计一个人考试成绩变化情况.
如果要了解数据的全部信息可以使用茎叶图.例如篮球比赛的记分.
因此要选择恰当的统计图表直观表达统计的数据,必须把各种统计图表的特点和问题中的需要结合起来,确定选择哪种统计图表.
题型一
条形统计图的应用
【例题1】某班计划开展一些课外活动,全班有40名学生报名参加,他们就乒乓球、足球、跳绳、羽毛球等4项活动的参加人数做了统计,绘制了条形统计图(如图所示),那么参加羽毛球活动的人数的频率是______.
反思:该例题中条形统计图的横轴是分组,纵轴是各组所含的个体数目.
题型二
扇形统计图的应用
【例题2】如图是甲、乙、丙、丁四组人数的扇形统计图的部分结果,根据扇形统计图的情况可以知道丙、丁两组人数和为( ).
A.250
B.150
C.400
D.300
反思:扇形统计图中各百分比是该组个体数目与总体数目的比,所有组的个体数目之和等于总体数目,所有组的百分比之和等于1.
题型三
折线统计图的应用
【例题3】下表给出了2010年A,B两地的降水量(单位:mm):
1月
2月
3月
4月
5月
6月
A
9.2
4.9
5.4
18.6
38.0
106.3
B
41.4
53.3
178.8
273.5
384.9
432.4
7月
8月
9月
10月
11月
12月
A
54.4
128.9
62.9
73.6
26.2
10.6
B
67.5
228.5
201.4
147.3
28.0
19.1
为了直观表示2010年A,B两地的降水量的差异和变化趋势,请用适当的统计图表示上面的数据.
反思:当两组数据具有可比性时,要想得出两组数据的差异,且能够直观观察出各组数据的分布趋势,常用折线统计图来表示.
题型四
茎叶图的应用
【例题4】某良种培育基地正在培育一种小麦新品种A,将其与原有的一个优良品种B进行对照试验,两种小麦各种植了25亩,所得亩产数据(单位:千克)如下:
品种A:357,359,367,368,375,388,392,399,400,405,412,414,415,421,423,423,427,430,430,434,443,445,445,451,454;
品种B:363,371,374,383,385,386,391,392,394,
394,395,397,397,400,401,401,403,406,407,410,412,415,416,422,430.
(1)根据上面数据画出茎叶图;
(2)用茎叶图处理现有的数据,有什么优点?
(3)通过观察茎叶图,对品种A与B的亩产量及其稳定性进行比较,写出统计结论.
分析:(1)茎是百位和十位,叶是个位;(2)依据茎叶图的优点写出即可;(3)观察出数据的平均水平就是亩产量的近似值,数据分散说明不稳定,数据集中说明稳定.
反思:茎叶图在样本数据较少但较为集中且数据有两位有效数字时比较适用.茎叶图有两个突出的优点,一是统计图上没有原始信息的损失,所有的数据信息都可以从茎叶图中得到;二是茎叶图可以在比赛时随时记录,方便记录和表示.
1当收集到的数据量很大或有多组数据时,需要比较各种数量的多少,用哪种统计图较合适( ).
A.茎叶图
B.条形统计图
C.折线统计图
D.扇形统计图
2如图是2009年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶图,则最低分和最高分分别为( ).
A.79,93
B.84,87
C.48,78
D.39,97
3某班学生在课外活动中参加文娱、美术、体育小组的人数之比为3∶1∶6,则在扇形统计图中表示参加体育小组人数的扇形圆心角是( ).
A.108°
B.216°
C.60°
D.36°
4甲、乙两个班级各随机选出15名同学进行测验,成绩的茎叶图如图所示,则甲班、乙班的最高成绩各是________,从图中看,________班的平均成绩较高.
5某地农村某户农民年收入如下(单位:元):
土地收入
打工收入
养殖收入
其他收入
4
320
3
600
2
357
843
请用不同的统计图来表示上面的数据.
答案:
基础知识·梳理
数据 结果 条形 扇形 折线
1.一个单位长度 数目
【做一做1】B
2.总体 部分占总体的百分比的大小 百分比
【做一做2】A
3.数量的多少 数量增减变化的情况 变化
【做一做3】D
4.(1)茎 叶 (2)信息 记录
【做一做4】45,45,52,56,57,58,60,63 由茎叶图可知销售数据都是两位数,分别为45,45,52,56,57,58,60,63.
典型例题·领悟
【例题1】0.1 参加羽毛球活动的人数是4,则频率为=0.1.
【例题2】A 甲组人数是120,占30%,则总人数是=400.则乙组人数是400×7.5%=30,则丙、丁两组人数和为400-120-30=250.
【例题3】解:用折线统计图表示题中的数据,如图.
其中虚线为B地降水量,实线为A地降水量.
【例题4】解:(1)茎叶图如图所示.
(2)用茎叶图处理现有的数据不仅可以看出数据的分布状况,而且可以看出每组中的具体数据.
(3)通过观察茎叶图,可以发现品种A的产量在420千克以上的亩数比品种B多10亩,而且品种A的产量在390千克以下的亩数与品种B一样多,由此可知,品种A的平均亩产量比品种B的平均亩产量高.但品种A的亩产量不够稳定,而品种B的亩产量比较集中,所以品种B的亩产量比较稳定.
随堂练习·巩固
1.
B 由于需要比较各种数量的多少,并且收集到的数据量很大或有多组数据,符合条形统计图的特点.
2.A
3.B 参加体育小组人数占总人数的×100%=60%,则扇形圆心角是360°×60%=216°.
4.96,92 乙
5.分析:题意的要求是将此四个数据用统计图表示出来,可利用条形统计图、折线统计图、扇形统计图来表示.
解:用条形统计图表示,如图所示.
用折线统计图表示,如图所示.
用扇形统计图表示,如图所示.
