1.3 统计图表 学案5(含答案)
图片预览



文档简介
1.3
统计图表
学案
课标解读
1.了解统计图表的作用与意义.2.理解茎叶图的概念并会应用(重点).3.会利用合适的统计图表研究生活中的例子(难点).
知识点1
条形统计图
【问题导思】
条形统计图的优点、缺点分别是什么?
【提示】 优点:(1)能够显示每组中的具体数据;
(2)易于比较数据间的差别.
缺点:不能明确显示部分与整体的对比.
条形统计图是用纵轴的一个单位表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按照一定的顺序排列起来.其特点是便于看出和比较各种数量的多少,即条形统计图能清楚地表示出每个项目的具体数据.
知识点二
折线统计图
【问题导思】
1.折线统计图中横轴上的点表示的是单个孤立的值还是样本值的范围?
【提示】 单个孤立的值.
2.折线统计图的优、缺点是什么?
【提示】 优点:可以表示数量的多少,直观地反映数量的增减情况,即变化趋势.
缺点:不适合总体分布较多的情况.
建立直角坐标系,用横轴上的数字表示样本值,用纵轴上的单位长度表示一定的数量,根据样本值和数量的多少描出相应点,然后用直线段顺次连接相邻点,得到一条折线,用这条折线表示样本数据情况,这种表述和分析数据的统计图称为折线统计图.
折线统计图不但可以表示数量的多少,而且能够用折线的起伏清楚直观地表示数量的增减变化的情况.
知识点三
扇形统计图
【问题导思】
扇形统计图的优缺点有哪些?
【提示】 优点:能直观显示总体中各部分的分布情况.
缺点:会丢失部分数据信息,且不适合总体中部分较多的情况.
扇形统计图中,用圆面积代表总体,圆面中的各个扇形分别代表总体中的不同部分,扇形面积的大小反映所表示的那部分占总体的百分比的大小.扇形统计图可以很清楚地表示各部分数量同总数之间的关系,即扇形统计图能清楚地表示出各部分在总体中所占的百分比.
知识点四
茎叶图
【问题导思】
1.茎叶图的茎和叶分别如何排列?
【提示】 (1)将每个数据分为茎(高位)和叶(低位)两部分;
(2)将表示茎的数字按大小顺序由上到下排成一列;
(3)将各个数据的叶按大小顺序写在茎相应的一侧.
2.茎叶图的优、缺点有哪些?
【提示】 优点:能保留原始数据,并可随时记录,记录和表示比较方便.
缺点:当数据量很大或有多组数据时不便于表示.
茎叶图的制作:茎相同的共用一个茎,茎按从小到大顺序从上到下列出,共茎的叶一般按从大到小或从小到大的顺序同时列出.
类型1
条形统计图
某人统计了一本书中的100个句子的字数,得出下列结果:1~5个字的15句,6~10个字的27句,11~15个字的32句,16~20个字的15句,21~25个字的8句,26~30个字的3句.
(1)试作出条形统计图;
(2)统计出1~15个字及16~30个字的句子个数所占百分比,作出条形统计图;
(3)统计出1~10个字,11~20个字,21~30个字的句子个数所占百分比,作出条形统计图.
【思路探究】 条形统计图中,横轴表示句子字数,纵轴表示句子个数,注意横轴、纵轴的刻度线要均匀,准确.
【自主解答】 (1)条形统计图如图(1)所示:
(2)1~15个字的句子个数为1~5个字,6~10个字,11~15个字的句子个数之和:15+27+32=74,所占百分比为74%;16~30个字的句子个数为16~20个字,21~25个字,25~30个字的句子个数之和:15+8+3=26,所占百分比为26%.条形统计如图(2)所示:
(3)1~10个字的句子个数为15+27=42,所占百分比为42%;11~20个字的句子个数为32+15=47,所占百分比为47%;21~30个字的句子个数为8+3=11,所占百分比为11%.条形统计图如图(3)所示.
1.依据题目的具体要求设置纵轴的含义.若图(1)的纵轴改为百分比,则各直条的数字表示相应的百分比.
2.从上述文字及统计图来看,从图(2)到图(3)再到图(1)反映的总体信息依次增多,且对相应字数的句子所占总体百分比的表述越来越精确.在实际问题中,我们常常根据问题的需要来选择不同的表达方式,以获得对数据的了解.
某班计划开展一些课外活动,全班有40名学生报名参加,他们就乒乓球、足球、跳绳、羽毛球等4项活动的参加人数做了统计,绘制了条形统计图(如图1-3-1所示),那么参加羽毛球活动的人数的频率是________.
图1-3-1
【解析】 参加羽毛球活动的人数为4,∴频率为=0.1.
【答案】 0.1
类型2
折线统计图
某摩托车厂2012年第三、四季度各月的月产量如下表:
月份
7
8
9
10
11
12
月产量(辆)
300
350
450
540
700
600
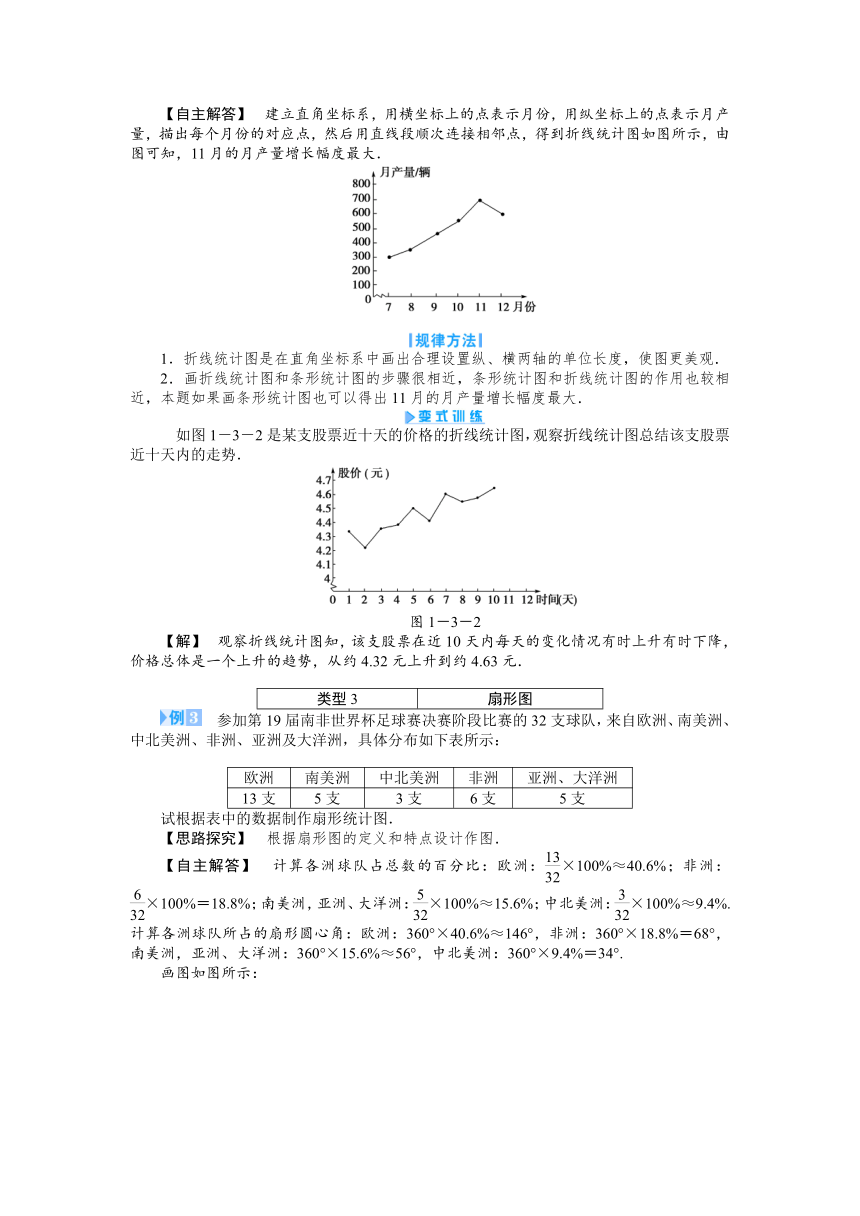
根据统计表绘制折线统计图,哪个月的月产量增长幅度最大?
【思路探究】 在绘制折线统计图时,可以先整理和观察数据统计表,建立直角坐标系,用两坐标轴上的点分别表示数据,再描出数据的相应点,顺次连接相邻的点,得到一条折线.
【自主解答】 建立直角坐标系,用横坐标上的点表示月份,用纵坐标上的点表示月产量,描出每个月份的对应点,然后用直线段顺次连接相邻点,得到折线统计图如图所示,由图可知,11月的月产量增长幅度最大.
1.折线统计图是在直角坐标系中画出合理设置纵、横两轴的单位长度,使图更美观.
2.画折线统计图和条形统计图的步骤很相近,条形统计图和折线统计图的作用也较相近,本题如果画条形统计图也可以得出11月的月产量增长幅度最大.
如图1-3-2是某支股票近十天的价格的折线统计图,观察折线统计图总结该支股票近十天内的走势.
图1-3-2
【解】 观察折线统计图知,该支股票在近10天内每天的变化情况有时上升有时下降,价格总体是一个上升的趋势,从约4.32元上升到约4.63元.
类型3
扇形图
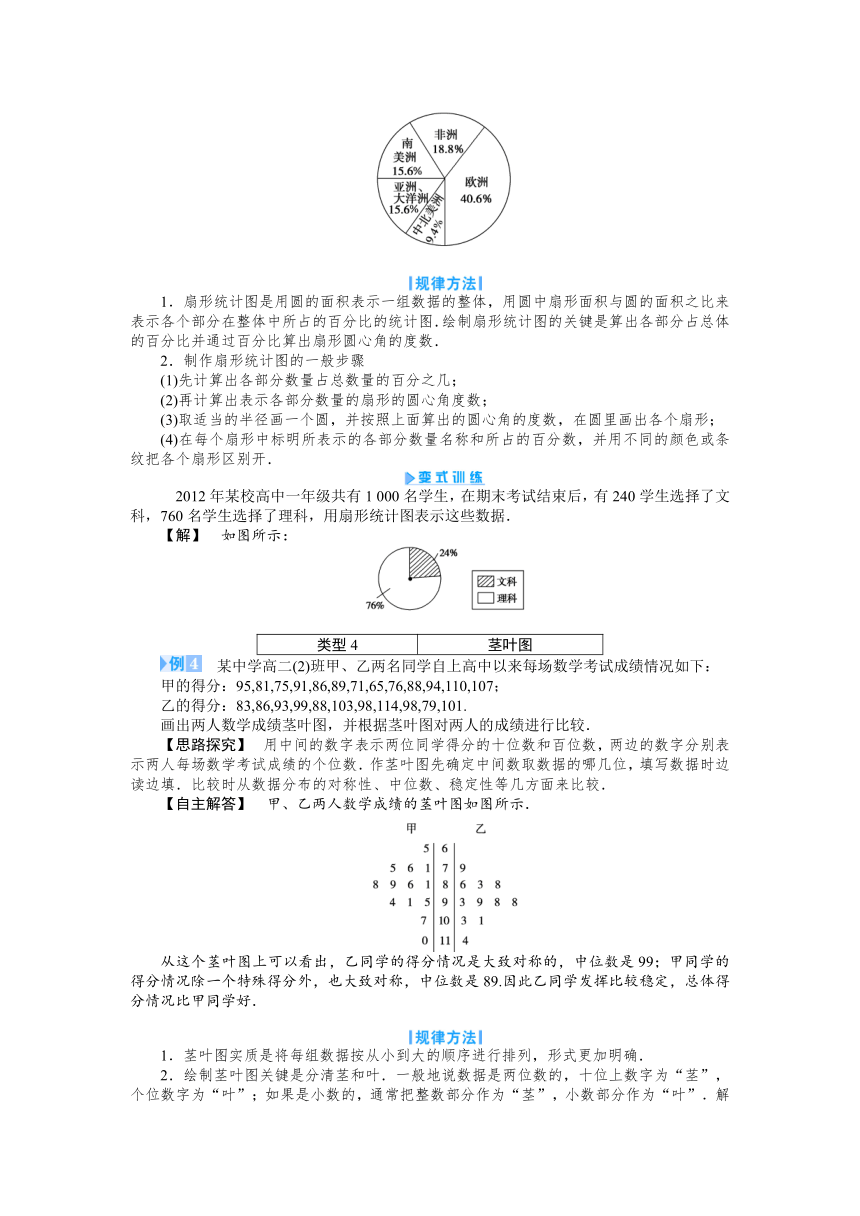
参加第19届南非世界杯足球赛决赛阶段比赛的32支球队,来自欧洲、南美洲、中北美洲、非洲、亚洲及大洋洲,具体分布如下表所示:
欧洲
南美洲
中北美洲
非洲
亚洲、大洋洲
13支
5支
3支
6支
5支
试根据表中的数据制作扇形统计图.
【思路探究】 根据扇形图的定义和特点设计作图.
【自主解答】 计算各洲球队占总数的百分比:欧洲:×100%≈40.6%;非洲:×100%=18.8%;南美洲,亚洲、大洋洲:×100%≈15.6%;中北美洲:×100%≈9.4%.计算各洲球队所占的扇形圆心角:欧洲:360°×40.6%≈146°,非洲:360°×18.8%=68°,南美洲,亚洲、大洋洲:360°×15.6%≈56°,中北美洲:360°×9.4%=34°.
画图如图所示:
1.扇形统计图是用圆的面积表示一组数据的整体,用圆中扇形面积与圆的面积之比来表示各个部分在整体中所占的百分比的统计图.绘制扇形统计图的关键是算出各部分占总体的百分比并通过百分比算出扇形圆心角的度数.
2.制作扇形统计图的一般步骤
(1)先计算出各部分数量占总数量的百分之几;
(2)再计算出表示各部分数量的扇形的圆心角度数;
(3)取适当的半径画一个圆,并按照上面算出的圆心角的度数,在圆里画出各个扇形;
(4)在每个扇形中标明所表示的各部分数量名称和所占的百分数,并用不同的颜色或条纹把各个扇形区别开.
2012年某校高中一年级共有1
000名学生,在期末考试结束后,有240学生选择了文科,760名学生选择了理科,用扇形统计图表示这些数据.
【解】 如图所示:
类型4
茎叶图
某中学高二(2)班甲、乙两名同学自上高中以来每场数学考试成绩情况如下:
甲的得分:95,81,75,91,86,89,71,65,76,88,94,110,107;
乙的得分:83,86,93,99,88,103,98,114,98,79,101.
画出两人数学成绩茎叶图,并根据茎叶图对两人的成绩进行比较.
【思路探究】 用中间的数字表示两位同学得分的十位数和百位数,两边的数字分别表示两人每场数学考试成绩的个位数.作茎叶图先确定中间数取数据的哪几位,填写数据时边读边填.比较时从数据分布的对称性、中位数、稳定性等几方面来比较.
【自主解答】 甲、乙两人数学成绩的茎叶图如图所示.
从这个茎叶图上可以看出,乙同学的得分情况是大致对称的,中位数是99;甲同学的得分情况除一个特殊得分外,也大致对称,中位数是89.因此乙同学发挥比较稳定,总体得分情况比甲同学好.
1.茎叶图实质是将每组数据按从小到大的顺序进行排列,形式更加明确.
2.绘制茎叶图关键是分清茎和叶.一般地说数据是两位数的,十位上数字为“茎”,个位数字为“叶”;如果是小数的,通常把整数部分作为“茎”,小数部分作为“叶”.解题时要根据数据特点合理选择茎和叶.
本例中将甲的得分普遍增加5分,再作比较.
【解】 甲、乙两人数学成绩的茎叶图如图所示.
从茎叶图上可以看出,乙同学的得分情况是大致对称的,中位数是99;甲同学的得分情况也是大致对称的,中位数为94.由茎叶图可知.乙同学发挥更稳定.
错画茎叶图致误
甲、乙两名篮球运动员上赛季每场比赛的得分如下:
甲:12,15,24,25,31,31,36,36,37,39,44,49,50;
乙:8,13,14,16,23,26,28,33,38,39,51.
试比较这两位运动员的得分水平.
【错解】
从茎叶图可以看出,甲得分大致对称,所以甲发挥得好.
【错因分析】 没有正确画出茎叶图,理由不充分.
【防范措施】 1.熟练掌握画茎叶图的方法和步骤.
2.对茎叶图的对称性及集中程度要明确.
【正解】 画出两人得分的茎叶图,为了便于对比分析,可将茎放在中间共用,叶分列左、右两侧.
从茎叶图可以看出,甲运动员的得分大致对称,平均得分、众数及中位数都是30多分,乙运动员的得分除一个51分外,也大致对称,平均得分及中位数都是20多分,因此甲运动员发挥得比较稳定,总体的得分情况比乙好.
四种统计图的优、缺点
统计图
优点
缺点
条形统计图
当数据量很大时,能直观地反映数据分布的大致情况,并且能清晰地表示出各个区间的具体数目
丢失部分数据信息
折线统计图
可以表示数量的多少,直观地反映数量的增减情况,即变化趋势
不适合总体分布较多的情况
扇形统计图
能直观显示总体中各部分的分布情况
会丢失部分数据信息,且不适合总体中部分较多的情况
茎叶图
能保留原始数据,并可随时记录,记录和表示比较方便
当数据量很大或有多组数据时不便于表示
1.下面哪种统计图没有数据信息的缺失,所有的原始数据都可以从该图中得到( )
A.条形统计图 B.茎叶图
C.扇形统计图
D.折线统计图
【解析】 由茎叶图的特点知,茎叶图满足上述条件.
【答案】 B
2.如图所示1-3-3是从一批产品中抽样得到的数据的条形统计图,由图可看出数据出现机会最大的范围是( )
图1-3-3
A.(8.1,8.3)
B.(8.2,8.4)
C.(8.4,8.5)
D.(8.6,8.7)
【解析】 由图易知数据出现在(8.2,8.4)范围内最大.
【答案】 B
3.如图1-3-4所示的两组数据中,波动比较大的是( )
图1-3-4
A.a组
B.b组
C.一样大
D.无法确定
【解析】 由折线图可知,a波动较大.
【答案】 A
4.某著名饮食品牌在某地开了甲、乙两家连锁店,一周内的每天回头客的数量统计结果如下:
甲:52 51 49 48 53 48 49
乙:60 65 40 35 25 65 60
用茎叶图分析哪个连锁店的客源比较稳定.
【解】 茎叶图如右图所示:
由茎叶图看出,甲连锁店的回头客数量比较集中,所以甲连锁店的客源比较稳定.
一、选择题
1.南美洲面积占地球陆地总面积的11.9%;
北美洲面积占地球陆地总面积的16.1%;
大洋洲面积占地球陆地总面积的6%;
南极洲面积占地球陆地总面积的9.3%.
想用统计图来描述这些数据,最合适的是( )
A.条形图 B.扇形图
C.折线图
D.茎叶图
【解析】 扇形图主要适用于所占百分比问题,故选B.
【答案】 B
2.观察省统计局公布的“十五”时期安徽省农村居民人均收入每年比上一年增长率的统计图(如图1-3-5所示),下列说法正确的是( )
图1-3-5
A.2003年农村居民人均收入低于2002年
B.农村居民人均收入比上一年增长率低于9%的有2年
C.农村居民人均收入最多是2004年
D.农村居民人均收入每年比上一年的增长率有大有小,但农村居民人均收入在持续增加
【解析】 由折线图给定的信息知从2001年到2005年每年的增长率都在增加,故农村居民人均收入始终持续增加.故选D.
【答案】 D
3.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自阅读课外书所用时间的数据,结果用条形图(如图1-3-6)表示,根据条形图可得这50名学生这一天平均每人的课外阅读时间为( )
图1-3-6
A.0.6
h
B.0.9
h
C.1.0
h
D.1.5
h
【解析】 由条形图知在被调查的50名同学中,有5人的课外阅读时间为2.0
h,有10人的课外阅读时间为1.5
h,有10人的课外阅读时间为1.0
h,有20人的课外阅读时间为0.5
h,有5人的课外阅读时间为0,故一天中平均每人的课外阅读时间为(5×0+5×2+10×1+10×1.5+20×0.5)=0.9(h).
【答案】 B
4.甲、乙两位同学在8次数学考试中的成绩的茎叶图如图1-3-7所示,则成绩比较稳定的为( )
图1-3-7
A.甲
B.乙
C.甲、乙一样
D.无法确定
【解析】 由茎叶图知甲的成绩有7次集中在80~90间,而乙的成绩则比较分散,故甲的成绩要比乙的成绩要稳定.
【答案】 A
5.(2012·江西高考)小波一星期的总开支分布如图(1)所示,一星期的食品开支如图(2)所示,则小波一星期的鸡蛋开支占总开支的百分比为( )
图(1)
图(2)
图1-3-8
A.30%
B.10%
C.3%
D.不能确定
【解析】 由题图(2)可知小波一星期的食品开支共计300元,其中鸡蛋开支30元.又由题图(1)知,一周的食品开支占总开支的30%,则可知一周总开支为1
000元,所以鸡蛋开支占总开支的百分比为×100%=3%.
【答案】 C
二、填空题
6.在2011暑期社会实践活动和社区服务中,小明所在小组的同学与一家玩具生产厂家联系,给该厂组装玩具,该厂同意他们组装240套玩具.这些玩具分为A、B、C三种型号,如图1-3-9所示:
图1-3-9
若每人组装同一种型号玩具的速度都相同,根据以上信息,完成下列空格:
(1)从上述统计图可知,A、B、C型玩具各有________、________、________套.
(2)若每人组装A型玩具16套与组装C型玩具12套所花的时间相同,那么a的值为________,每人每小时组装C型玩具________套.
【解析】 A型有240×55%=132(套),B型240×20%=48(套),C型有240×25%=60(套).
(2)由题图左图可知每人组装A型玩具16套用2小时,所以组装C型玩具12套用2小时,则每小时组装6套,由2a-2=6,得a=4.
【答案】 (1)132 48 60 (2)4 6
7.如图是某市5月1日至5月7日每天最高、最低气温的折线统计图,在这7天中,日温差最大的一天是________.
图1-3-10
【解析】 由图知5月1日~5月7日的温差分别为:12
℃,12
℃,11
℃,10.5
℃,12.5
℃,10
℃,10
℃,故5月5日温差最大.
【答案】 5月5日
8.(2013·上饶检测)某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用分层抽样法,将全体职工随机按1~200编号,则50岁以上年龄段应抽取________人.
图1-3-11
【解析】 50岁以上的职工数为200×20%=40人按分层抽样法应抽取的人数为40×=8.
【答案】 8
三、解答题
9.英才学校的四个年级学生分布如图①所示的扇形统计图,通过对全体学生暑假期间所读课外书情况的调查,制成各年级读书情况的条形统计图(如图②).已知英才学校被调查的四个年级共有学生1
500人,求:
① ②
图1-3-12
(1)高一年级学生暑假期间共读课外书的本数;
(2)暑假期间读课外书总量最少的是几年级学生,共读课外书的本数.
【解】 (1)因为高一年级学生占总人数的百分比为1-24%-28%-22%=26%,共有1
500人,所以高一年级有1
500×26%=390(人),每人读6.2本,故高一年级学生暑假期间共读课外书390×6.2=2
418(本).
(2)七年级参加调查的人数有1
500×28%=420(人),阅读课外书总量为420×5.6=2
352(本);八年级参加调查的人数有1
500×24%=360(人),阅读课外书总量为360×6.6=2
376(本);高二年级参加调查的人数有1
500×22%=330(人),阅读课外书总量为330×7.3=2
409(本),故暑假期间阅读课外书总量最少的是七年级学生,共读课外书2
352本.
10.甲、乙两个小组各10名学生,这20名学生某次英语口语测试的成绩如下(单位:分):
甲组 76 90 84 86 81 87 86 82 85 83
乙组 82 84 85 89 79 80 91 89 79 74
用茎叶图表示两个小组的成绩,并判断哪个小组的成绩更整齐一些.
【解】 茎叶图如下图所示:
由图容易看出甲组成绩较集中,即甲组的成绩更整齐一些.
11.某地农村某户农民年收入如下(单位:元):
土地收入
打工收入
养殖收入
其他收入
4
320
3
600
2
357
843
请用不同的统计图来表示上面的数据.
【解】 用条形统计图表示,如图所示:
用折线统计图表示,如图所示:
用扇形统计图表示,如图所示:
统计图表
学案
课标解读
1.了解统计图表的作用与意义.2.理解茎叶图的概念并会应用(重点).3.会利用合适的统计图表研究生活中的例子(难点).
知识点1
条形统计图
【问题导思】
条形统计图的优点、缺点分别是什么?
【提示】 优点:(1)能够显示每组中的具体数据;
(2)易于比较数据间的差别.
缺点:不能明确显示部分与整体的对比.
条形统计图是用纵轴的一个单位表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按照一定的顺序排列起来.其特点是便于看出和比较各种数量的多少,即条形统计图能清楚地表示出每个项目的具体数据.
知识点二
折线统计图
【问题导思】
1.折线统计图中横轴上的点表示的是单个孤立的值还是样本值的范围?
【提示】 单个孤立的值.
2.折线统计图的优、缺点是什么?
【提示】 优点:可以表示数量的多少,直观地反映数量的增减情况,即变化趋势.
缺点:不适合总体分布较多的情况.
建立直角坐标系,用横轴上的数字表示样本值,用纵轴上的单位长度表示一定的数量,根据样本值和数量的多少描出相应点,然后用直线段顺次连接相邻点,得到一条折线,用这条折线表示样本数据情况,这种表述和分析数据的统计图称为折线统计图.
折线统计图不但可以表示数量的多少,而且能够用折线的起伏清楚直观地表示数量的增减变化的情况.
知识点三
扇形统计图
【问题导思】
扇形统计图的优缺点有哪些?
【提示】 优点:能直观显示总体中各部分的分布情况.
缺点:会丢失部分数据信息,且不适合总体中部分较多的情况.
扇形统计图中,用圆面积代表总体,圆面中的各个扇形分别代表总体中的不同部分,扇形面积的大小反映所表示的那部分占总体的百分比的大小.扇形统计图可以很清楚地表示各部分数量同总数之间的关系,即扇形统计图能清楚地表示出各部分在总体中所占的百分比.
知识点四
茎叶图
【问题导思】
1.茎叶图的茎和叶分别如何排列?
【提示】 (1)将每个数据分为茎(高位)和叶(低位)两部分;
(2)将表示茎的数字按大小顺序由上到下排成一列;
(3)将各个数据的叶按大小顺序写在茎相应的一侧.
2.茎叶图的优、缺点有哪些?
【提示】 优点:能保留原始数据,并可随时记录,记录和表示比较方便.
缺点:当数据量很大或有多组数据时不便于表示.
茎叶图的制作:茎相同的共用一个茎,茎按从小到大顺序从上到下列出,共茎的叶一般按从大到小或从小到大的顺序同时列出.
类型1
条形统计图
某人统计了一本书中的100个句子的字数,得出下列结果:1~5个字的15句,6~10个字的27句,11~15个字的32句,16~20个字的15句,21~25个字的8句,26~30个字的3句.
(1)试作出条形统计图;
(2)统计出1~15个字及16~30个字的句子个数所占百分比,作出条形统计图;
(3)统计出1~10个字,11~20个字,21~30个字的句子个数所占百分比,作出条形统计图.
【思路探究】 条形统计图中,横轴表示句子字数,纵轴表示句子个数,注意横轴、纵轴的刻度线要均匀,准确.
【自主解答】 (1)条形统计图如图(1)所示:
(2)1~15个字的句子个数为1~5个字,6~10个字,11~15个字的句子个数之和:15+27+32=74,所占百分比为74%;16~30个字的句子个数为16~20个字,21~25个字,25~30个字的句子个数之和:15+8+3=26,所占百分比为26%.条形统计如图(2)所示:
(3)1~10个字的句子个数为15+27=42,所占百分比为42%;11~20个字的句子个数为32+15=47,所占百分比为47%;21~30个字的句子个数为8+3=11,所占百分比为11%.条形统计图如图(3)所示.
1.依据题目的具体要求设置纵轴的含义.若图(1)的纵轴改为百分比,则各直条的数字表示相应的百分比.
2.从上述文字及统计图来看,从图(2)到图(3)再到图(1)反映的总体信息依次增多,且对相应字数的句子所占总体百分比的表述越来越精确.在实际问题中,我们常常根据问题的需要来选择不同的表达方式,以获得对数据的了解.
某班计划开展一些课外活动,全班有40名学生报名参加,他们就乒乓球、足球、跳绳、羽毛球等4项活动的参加人数做了统计,绘制了条形统计图(如图1-3-1所示),那么参加羽毛球活动的人数的频率是________.
图1-3-1
【解析】 参加羽毛球活动的人数为4,∴频率为=0.1.
【答案】 0.1
类型2
折线统计图
某摩托车厂2012年第三、四季度各月的月产量如下表:
月份
7
8
9
10
11
12
月产量(辆)
300
350
450
540
700
600
根据统计表绘制折线统计图,哪个月的月产量增长幅度最大?
【思路探究】 在绘制折线统计图时,可以先整理和观察数据统计表,建立直角坐标系,用两坐标轴上的点分别表示数据,再描出数据的相应点,顺次连接相邻的点,得到一条折线.
【自主解答】 建立直角坐标系,用横坐标上的点表示月份,用纵坐标上的点表示月产量,描出每个月份的对应点,然后用直线段顺次连接相邻点,得到折线统计图如图所示,由图可知,11月的月产量增长幅度最大.
1.折线统计图是在直角坐标系中画出合理设置纵、横两轴的单位长度,使图更美观.
2.画折线统计图和条形统计图的步骤很相近,条形统计图和折线统计图的作用也较相近,本题如果画条形统计图也可以得出11月的月产量增长幅度最大.
如图1-3-2是某支股票近十天的价格的折线统计图,观察折线统计图总结该支股票近十天内的走势.
图1-3-2
【解】 观察折线统计图知,该支股票在近10天内每天的变化情况有时上升有时下降,价格总体是一个上升的趋势,从约4.32元上升到约4.63元.
类型3
扇形图
参加第19届南非世界杯足球赛决赛阶段比赛的32支球队,来自欧洲、南美洲、中北美洲、非洲、亚洲及大洋洲,具体分布如下表所示:
欧洲
南美洲
中北美洲
非洲
亚洲、大洋洲
13支
5支
3支
6支
5支
试根据表中的数据制作扇形统计图.
【思路探究】 根据扇形图的定义和特点设计作图.
【自主解答】 计算各洲球队占总数的百分比:欧洲:×100%≈40.6%;非洲:×100%=18.8%;南美洲,亚洲、大洋洲:×100%≈15.6%;中北美洲:×100%≈9.4%.计算各洲球队所占的扇形圆心角:欧洲:360°×40.6%≈146°,非洲:360°×18.8%=68°,南美洲,亚洲、大洋洲:360°×15.6%≈56°,中北美洲:360°×9.4%=34°.
画图如图所示:
1.扇形统计图是用圆的面积表示一组数据的整体,用圆中扇形面积与圆的面积之比来表示各个部分在整体中所占的百分比的统计图.绘制扇形统计图的关键是算出各部分占总体的百分比并通过百分比算出扇形圆心角的度数.
2.制作扇形统计图的一般步骤
(1)先计算出各部分数量占总数量的百分之几;
(2)再计算出表示各部分数量的扇形的圆心角度数;
(3)取适当的半径画一个圆,并按照上面算出的圆心角的度数,在圆里画出各个扇形;
(4)在每个扇形中标明所表示的各部分数量名称和所占的百分数,并用不同的颜色或条纹把各个扇形区别开.
2012年某校高中一年级共有1
000名学生,在期末考试结束后,有240学生选择了文科,760名学生选择了理科,用扇形统计图表示这些数据.
【解】 如图所示:
类型4
茎叶图
某中学高二(2)班甲、乙两名同学自上高中以来每场数学考试成绩情况如下:
甲的得分:95,81,75,91,86,89,71,65,76,88,94,110,107;
乙的得分:83,86,93,99,88,103,98,114,98,79,101.
画出两人数学成绩茎叶图,并根据茎叶图对两人的成绩进行比较.
【思路探究】 用中间的数字表示两位同学得分的十位数和百位数,两边的数字分别表示两人每场数学考试成绩的个位数.作茎叶图先确定中间数取数据的哪几位,填写数据时边读边填.比较时从数据分布的对称性、中位数、稳定性等几方面来比较.
【自主解答】 甲、乙两人数学成绩的茎叶图如图所示.
从这个茎叶图上可以看出,乙同学的得分情况是大致对称的,中位数是99;甲同学的得分情况除一个特殊得分外,也大致对称,中位数是89.因此乙同学发挥比较稳定,总体得分情况比甲同学好.
1.茎叶图实质是将每组数据按从小到大的顺序进行排列,形式更加明确.
2.绘制茎叶图关键是分清茎和叶.一般地说数据是两位数的,十位上数字为“茎”,个位数字为“叶”;如果是小数的,通常把整数部分作为“茎”,小数部分作为“叶”.解题时要根据数据特点合理选择茎和叶.
本例中将甲的得分普遍增加5分,再作比较.
【解】 甲、乙两人数学成绩的茎叶图如图所示.
从茎叶图上可以看出,乙同学的得分情况是大致对称的,中位数是99;甲同学的得分情况也是大致对称的,中位数为94.由茎叶图可知.乙同学发挥更稳定.
错画茎叶图致误
甲、乙两名篮球运动员上赛季每场比赛的得分如下:
甲:12,15,24,25,31,31,36,36,37,39,44,49,50;
乙:8,13,14,16,23,26,28,33,38,39,51.
试比较这两位运动员的得分水平.
【错解】
从茎叶图可以看出,甲得分大致对称,所以甲发挥得好.
【错因分析】 没有正确画出茎叶图,理由不充分.
【防范措施】 1.熟练掌握画茎叶图的方法和步骤.
2.对茎叶图的对称性及集中程度要明确.
【正解】 画出两人得分的茎叶图,为了便于对比分析,可将茎放在中间共用,叶分列左、右两侧.
从茎叶图可以看出,甲运动员的得分大致对称,平均得分、众数及中位数都是30多分,乙运动员的得分除一个51分外,也大致对称,平均得分及中位数都是20多分,因此甲运动员发挥得比较稳定,总体的得分情况比乙好.
四种统计图的优、缺点
统计图
优点
缺点
条形统计图
当数据量很大时,能直观地反映数据分布的大致情况,并且能清晰地表示出各个区间的具体数目
丢失部分数据信息
折线统计图
可以表示数量的多少,直观地反映数量的增减情况,即变化趋势
不适合总体分布较多的情况
扇形统计图
能直观显示总体中各部分的分布情况
会丢失部分数据信息,且不适合总体中部分较多的情况
茎叶图
能保留原始数据,并可随时记录,记录和表示比较方便
当数据量很大或有多组数据时不便于表示
1.下面哪种统计图没有数据信息的缺失,所有的原始数据都可以从该图中得到( )
A.条形统计图 B.茎叶图
C.扇形统计图
D.折线统计图
【解析】 由茎叶图的特点知,茎叶图满足上述条件.
【答案】 B
2.如图所示1-3-3是从一批产品中抽样得到的数据的条形统计图,由图可看出数据出现机会最大的范围是( )
图1-3-3
A.(8.1,8.3)
B.(8.2,8.4)
C.(8.4,8.5)
D.(8.6,8.7)
【解析】 由图易知数据出现在(8.2,8.4)范围内最大.
【答案】 B
3.如图1-3-4所示的两组数据中,波动比较大的是( )
图1-3-4
A.a组
B.b组
C.一样大
D.无法确定
【解析】 由折线图可知,a波动较大.
【答案】 A
4.某著名饮食品牌在某地开了甲、乙两家连锁店,一周内的每天回头客的数量统计结果如下:
甲:52 51 49 48 53 48 49
乙:60 65 40 35 25 65 60
用茎叶图分析哪个连锁店的客源比较稳定.
【解】 茎叶图如右图所示:
由茎叶图看出,甲连锁店的回头客数量比较集中,所以甲连锁店的客源比较稳定.
一、选择题
1.南美洲面积占地球陆地总面积的11.9%;
北美洲面积占地球陆地总面积的16.1%;
大洋洲面积占地球陆地总面积的6%;
南极洲面积占地球陆地总面积的9.3%.
想用统计图来描述这些数据,最合适的是( )
A.条形图 B.扇形图
C.折线图
D.茎叶图
【解析】 扇形图主要适用于所占百分比问题,故选B.
【答案】 B
2.观察省统计局公布的“十五”时期安徽省农村居民人均收入每年比上一年增长率的统计图(如图1-3-5所示),下列说法正确的是( )
图1-3-5
A.2003年农村居民人均收入低于2002年
B.农村居民人均收入比上一年增长率低于9%的有2年
C.农村居民人均收入最多是2004年
D.农村居民人均收入每年比上一年的增长率有大有小,但农村居民人均收入在持续增加
【解析】 由折线图给定的信息知从2001年到2005年每年的增长率都在增加,故农村居民人均收入始终持续增加.故选D.
【答案】 D
3.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自阅读课外书所用时间的数据,结果用条形图(如图1-3-6)表示,根据条形图可得这50名学生这一天平均每人的课外阅读时间为( )
图1-3-6
A.0.6
h
B.0.9
h
C.1.0
h
D.1.5
h
【解析】 由条形图知在被调查的50名同学中,有5人的课外阅读时间为2.0
h,有10人的课外阅读时间为1.5
h,有10人的课外阅读时间为1.0
h,有20人的课外阅读时间为0.5
h,有5人的课外阅读时间为0,故一天中平均每人的课外阅读时间为(5×0+5×2+10×1+10×1.5+20×0.5)=0.9(h).
【答案】 B
4.甲、乙两位同学在8次数学考试中的成绩的茎叶图如图1-3-7所示,则成绩比较稳定的为( )
图1-3-7
A.甲
B.乙
C.甲、乙一样
D.无法确定
【解析】 由茎叶图知甲的成绩有7次集中在80~90间,而乙的成绩则比较分散,故甲的成绩要比乙的成绩要稳定.
【答案】 A
5.(2012·江西高考)小波一星期的总开支分布如图(1)所示,一星期的食品开支如图(2)所示,则小波一星期的鸡蛋开支占总开支的百分比为( )
图(1)
图(2)
图1-3-8
A.30%
B.10%
C.3%
D.不能确定
【解析】 由题图(2)可知小波一星期的食品开支共计300元,其中鸡蛋开支30元.又由题图(1)知,一周的食品开支占总开支的30%,则可知一周总开支为1
000元,所以鸡蛋开支占总开支的百分比为×100%=3%.
【答案】 C
二、填空题
6.在2011暑期社会实践活动和社区服务中,小明所在小组的同学与一家玩具生产厂家联系,给该厂组装玩具,该厂同意他们组装240套玩具.这些玩具分为A、B、C三种型号,如图1-3-9所示:
图1-3-9
若每人组装同一种型号玩具的速度都相同,根据以上信息,完成下列空格:
(1)从上述统计图可知,A、B、C型玩具各有________、________、________套.
(2)若每人组装A型玩具16套与组装C型玩具12套所花的时间相同,那么a的值为________,每人每小时组装C型玩具________套.
【解析】 A型有240×55%=132(套),B型240×20%=48(套),C型有240×25%=60(套).
(2)由题图左图可知每人组装A型玩具16套用2小时,所以组装C型玩具12套用2小时,则每小时组装6套,由2a-2=6,得a=4.
【答案】 (1)132 48 60 (2)4 6
7.如图是某市5月1日至5月7日每天最高、最低气温的折线统计图,在这7天中,日温差最大的一天是________.
图1-3-10
【解析】 由图知5月1日~5月7日的温差分别为:12
℃,12
℃,11
℃,10.5
℃,12.5
℃,10
℃,10
℃,故5月5日温差最大.
【答案】 5月5日
8.(2013·上饶检测)某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用分层抽样法,将全体职工随机按1~200编号,则50岁以上年龄段应抽取________人.
图1-3-11
【解析】 50岁以上的职工数为200×20%=40人按分层抽样法应抽取的人数为40×=8.
【答案】 8
三、解答题
9.英才学校的四个年级学生分布如图①所示的扇形统计图,通过对全体学生暑假期间所读课外书情况的调查,制成各年级读书情况的条形统计图(如图②).已知英才学校被调查的四个年级共有学生1
500人,求:
① ②
图1-3-12
(1)高一年级学生暑假期间共读课外书的本数;
(2)暑假期间读课外书总量最少的是几年级学生,共读课外书的本数.
【解】 (1)因为高一年级学生占总人数的百分比为1-24%-28%-22%=26%,共有1
500人,所以高一年级有1
500×26%=390(人),每人读6.2本,故高一年级学生暑假期间共读课外书390×6.2=2
418(本).
(2)七年级参加调查的人数有1
500×28%=420(人),阅读课外书总量为420×5.6=2
352(本);八年级参加调查的人数有1
500×24%=360(人),阅读课外书总量为360×6.6=2
376(本);高二年级参加调查的人数有1
500×22%=330(人),阅读课外书总量为330×7.3=2
409(本),故暑假期间阅读课外书总量最少的是七年级学生,共读课外书2
352本.
10.甲、乙两个小组各10名学生,这20名学生某次英语口语测试的成绩如下(单位:分):
甲组 76 90 84 86 81 87 86 82 85 83
乙组 82 84 85 89 79 80 91 89 79 74
用茎叶图表示两个小组的成绩,并判断哪个小组的成绩更整齐一些.
【解】 茎叶图如下图所示:
由图容易看出甲组成绩较集中,即甲组的成绩更整齐一些.
11.某地农村某户农民年收入如下(单位:元):
土地收入
打工收入
养殖收入
其他收入
4
320
3
600
2
357
843
请用不同的统计图来表示上面的数据.
【解】 用条形统计图表示,如图所示:
用折线统计图表示,如图所示:
用扇形统计图表示,如图所示:
