1.5.1 估计总体的分布 学案1(含答案)
文档属性
| 名称 | 1.5.1 估计总体的分布 学案1(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 70.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-16 18:54:17 | ||
图片预览




文档简介
1.5.1
估计总体的分布
学案
一、学习目标
1.通过实例体会分布的意义和作用.
2.在表示样本数据的过程中,学会列频率分布表,画频率分布直方图、频率折线图.
3.通过实例体会频率分布直方图、频率折线图、的各自特征,从而恰当地选择上述方法分析样本的分布,准确地做出总体估计.
二、重点、难点
重点:会列频率分布表,画频率分布直方图、频率折线图.
难点:能通过样本的频率分布估计总体的分布.
三、课前预习
1.频率分布的概念:
〖探究〗:同样一组数据,如果组距不同,横轴、纵轴的单位不同,得到的图和形状也会不同。不同的形状给人以不同的印象,这种印象有时会影响我们对总体的判断,分别以0.1和1为组距重新作图,然后谈谈你对图的印象?(把学生分成两大组进行,分别作出两种组距的图,然后组织同学们对所作图不同的看法进行交流……)
2.频率分布折线图:
四、堂中互动
【教师点拨】1.画频率分布直方图一般步骤:①找最值,算极差,确定组距②分组决定各组分点,累计各组的频数③画图.画图时特别要注意纵坐标是,还要标明横坐标表示什么及其单位.
2.利用样本在某一范围内的频率,可以近似地估计总体在这一范围内的频率.
例.下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高(单位cm)
(1)列出样本频率分布表;
(2)画出频率分布直方图;
(3)估计身高小于134cm的人数占总人数的百分比.
点评:列出样本频率分布表或画出频率分布直方图主要是要熟练掌握它们的步骤.
五、即学即练
1.在用样本频率估计总体分布的过程中,下列说法中正确的是(
)
A.总体容量越大,估计越精确
B.总体容量越小,估计越精确
C.样本容量越大,估计越精确
D.样本容量越小,估计越精确
2.有一个容量为45的样本数据,分组后,各组频数如下:
[12.5,15.5)
3,
[15.5,18.5)
8,
[18.5,21.5)
9,
[21.5,24.5)
11,
[24.5,27.5)
10,
[27.5,30.5)
4。
根据累计频率分布,估计小于27.5的数据约为总体的(
)
A.91%
B.30%
C.92%
D.95%
3.有一个容量为20的样本数据,分组后,组距与各组频数如下:
[10,20)
2,
[20,30)
3,
[30,40)
4,
[40,50)
5,
[50,60)
4,
[60,70)
2.
则样本在区间
[10,50)上的频率为(
)
A.5%
B.25%
C.50%
D.70%
练案
A组
1.将容量为n的样本中的数据分成6组,绘制频率分布直方图.若第一组至第六组数据的频率之比为2:3:4:6:4:1,且前三组数据的频数之和等于27,则n等于
.
2.某校为了了解学生的课外阅读情况,随机调查了50名学生,
得到他们在某一天各自课外阅读所用时间的数据,结果用右侧的条
形图表示.
根据条形图可得这50名学生这一天平均每人的课外阅读
时间为
(
)
A.0.6小时
B.0.9小时
C.1.0小时
D.1.5小时
3.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a,
b的值分别为(
)
A.0,27,78
B.0,27,83
C.2.7,78
D.2.7,83
4.用条形图表示下表中关注不同广告的人数、频率。
广告类型
人数
比例
频率%
商品广告
112
0.560
56
服务广告
51
0.255
25.5
金融广告
9
0.045
4.5
房地产广告
16
0.080
8
招生招聘广告
10
0.050
5
其他广告
2
0.010
1
合计
200
1.000
100
5.从全校参加科技知识竞赛的学生试卷中,抽取一个样本,考察竞赛的成绩分布.将样本分成5组,绘成频率分布直方图(如图),图中从左到右各小组的小长方形的高的比是1∶3∶6∶4∶2,最后边一组的频数是6.请结合频率分布直方图提供的信息,解答下列问题:
(1)样本的容量是多少?
(2)列出频率分布表;
(3)成绩落在哪个范围内的人数最多 并求该小组的频数、频率;
(4)估计这次竞赛中,成绩不低于60分的学生占总人数的百分比.
B组
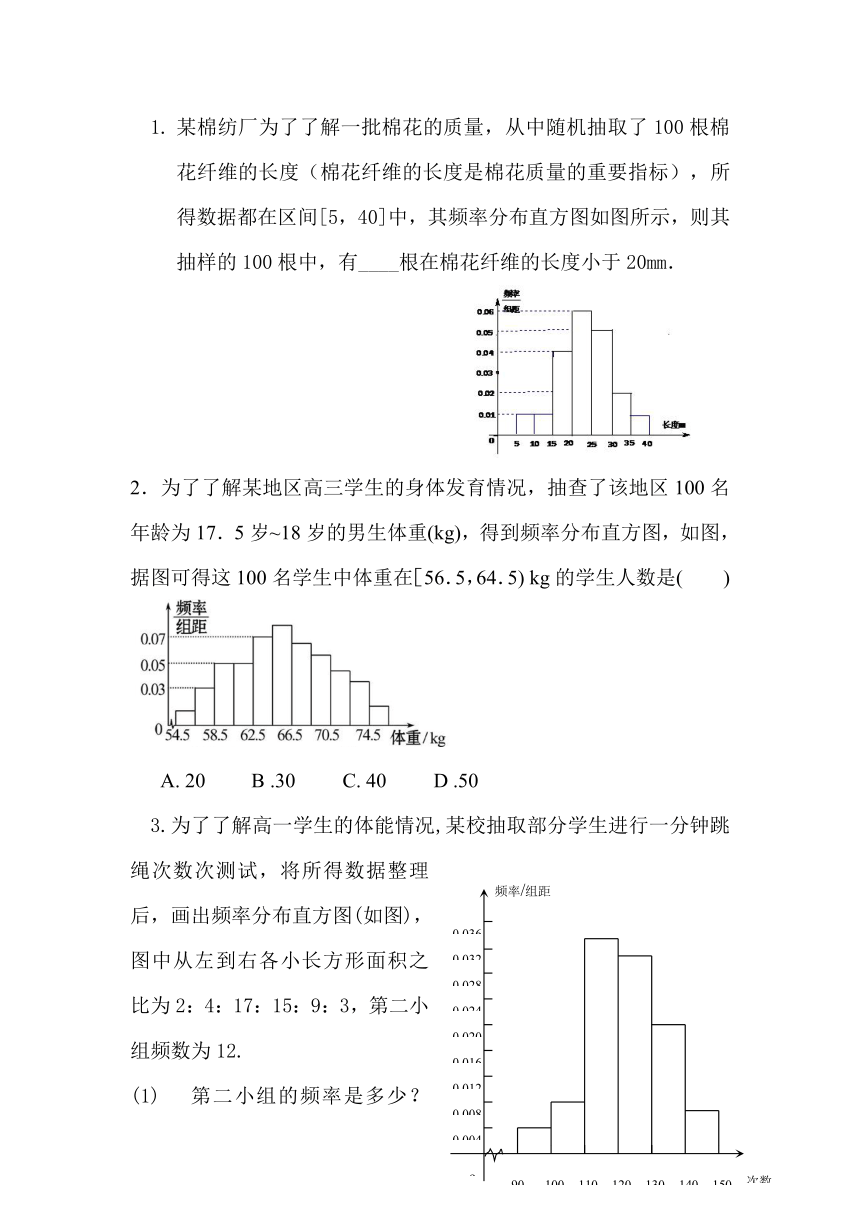
某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示,则其抽样的100根中,有____根在棉花纤维的长度小于20mm.
2.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图,如图,据图可得这100名学生中体重在[56.5,64.5)
kg的学生人数是(
)
A.
20
B
.30
C.
40
D
.50
3.为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
第二小组的频率是多少?样本容量是多少?
若次数在110以上(含110次)为达标,试估计
该学校全体高一学生的达标率是多少?
在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由。
1.5.1
估计总体的分布
答案
三、课前预习
1.频率分布是指一个样本数据在各个小范围内所占比例的大小。一般用频率分布直方图反映样本的频率分布。其一般步骤为:计算一组数据中最大值与最小值的差,即求极差(1)决定组距与组数;⑵将数据分组;⑶列频率分布表;⑷画频率分布直方图。
以课本P32106块头盖骨分布问题为例,经过以上几个步骤画出频率分布直方图。(让学生自己动手作图)
频率分布直方图的特征:⑴从频率分布直方图可以清楚的看出数据分布的总体趋势。⑵从频率分布直方图得不出原始的数据内容,把数据表示成直方图后,原有的具体数据信息就被抹掉了。
2.连接频率分布直方图中各小长方形上端的中点,就得到频率分布折线图。
四、堂中互动
解:(1)样本频率分布表如下:
(2)其频率分布直方图如下:
(3)由样本频率分布表可知身高小于134cm
的男孩出现的频率为0.04+0.07+0.08=0.19,所以我们估计身高小于134cm的人数占总人数的19%.
五、即学即练
1.
C
2.A
3.D
练案
A组
1.
60
2.B
3.A
4.解:人数分布条形图如下
频率分布条形图如下
5.解:(1)由于各组的组距相等,所以各组的频率与各小长方形的高成正比且各组频率的和等于1,那么各组的频率分别为,,,,.设该样本容量为n,则=,所以样本容量为n=48.
(2)由以上得频率分布表如下:
成绩
频数
频率
[50.5,60.5)
3
[60.5,70.5)
9
[70.5,80.5)
18
[80.5,90.5)
12
[90.5,100.5)
6
合计
48
1
(3)成绩落在[70.5,80.5)之间的人数最多,该组的频数和频率分别是18和.
(4)不低于60分的学生占总人数的百分比约为
×100%≈94%.
B组
1.35
2.A
3.分析:在频率分布直方图中,各小长方形的面积等于相应各组的频率,小长方形的高与频数成正比,各组频数之和等于样本容量,频率之和等于1。
解:(1)由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小,因此第二小组的频率为:又因为频率=
所以
(2)由图可估计该学校高一学生的达标率约为
(3)由已知可得各小组的频数依次为6,12,51,45,27,9,所以前三组的频数之和为69,前四组的频数之和为114,所以跳绳次数的中位数落在第四小组内。
0.5
人数(人)
时间(小时)
20
10
5
0
1.0
1.5
2.0
15
0.3
0.1
4.3
4.4
4.5
4.6
4.7
4.8
4.9
5.0
5.1
5.2
视力
90
100
110
120
130
140
150
次数
o
0.004
0.008
0.012
0.016
0.020
0.024
0.028
频率/组距
0.032
0.036
122
126
130
134
138
142
146
150
158
154
身高(cm)
o
0.01
0.02
0.03
0.04
0.05
0.06
0.07
频率/组距
估计总体的分布
学案
一、学习目标
1.通过实例体会分布的意义和作用.
2.在表示样本数据的过程中,学会列频率分布表,画频率分布直方图、频率折线图.
3.通过实例体会频率分布直方图、频率折线图、的各自特征,从而恰当地选择上述方法分析样本的分布,准确地做出总体估计.
二、重点、难点
重点:会列频率分布表,画频率分布直方图、频率折线图.
难点:能通过样本的频率分布估计总体的分布.
三、课前预习
1.频率分布的概念:
〖探究〗:同样一组数据,如果组距不同,横轴、纵轴的单位不同,得到的图和形状也会不同。不同的形状给人以不同的印象,这种印象有时会影响我们对总体的判断,分别以0.1和1为组距重新作图,然后谈谈你对图的印象?(把学生分成两大组进行,分别作出两种组距的图,然后组织同学们对所作图不同的看法进行交流……)
2.频率分布折线图:
四、堂中互动
【教师点拨】1.画频率分布直方图一般步骤:①找最值,算极差,确定组距②分组决定各组分点,累计各组的频数③画图.画图时特别要注意纵坐标是,还要标明横坐标表示什么及其单位.
2.利用样本在某一范围内的频率,可以近似地估计总体在这一范围内的频率.
例.下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高(单位cm)
(1)列出样本频率分布表;
(2)画出频率分布直方图;
(3)估计身高小于134cm的人数占总人数的百分比.
点评:列出样本频率分布表或画出频率分布直方图主要是要熟练掌握它们的步骤.
五、即学即练
1.在用样本频率估计总体分布的过程中,下列说法中正确的是(
)
A.总体容量越大,估计越精确
B.总体容量越小,估计越精确
C.样本容量越大,估计越精确
D.样本容量越小,估计越精确
2.有一个容量为45的样本数据,分组后,各组频数如下:
[12.5,15.5)
3,
[15.5,18.5)
8,
[18.5,21.5)
9,
[21.5,24.5)
11,
[24.5,27.5)
10,
[27.5,30.5)
4。
根据累计频率分布,估计小于27.5的数据约为总体的(
)
A.91%
B.30%
C.92%
D.95%
3.有一个容量为20的样本数据,分组后,组距与各组频数如下:
[10,20)
2,
[20,30)
3,
[30,40)
4,
[40,50)
5,
[50,60)
4,
[60,70)
2.
则样本在区间
[10,50)上的频率为(
)
A.5%
B.25%
C.50%
D.70%
练案
A组
1.将容量为n的样本中的数据分成6组,绘制频率分布直方图.若第一组至第六组数据的频率之比为2:3:4:6:4:1,且前三组数据的频数之和等于27,则n等于
.
2.某校为了了解学生的课外阅读情况,随机调查了50名学生,
得到他们在某一天各自课外阅读所用时间的数据,结果用右侧的条
形图表示.
根据条形图可得这50名学生这一天平均每人的课外阅读
时间为
(
)
A.0.6小时
B.0.9小时
C.1.0小时
D.1.5小时
3.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a,
b的值分别为(
)
A.0,27,78
B.0,27,83
C.2.7,78
D.2.7,83
4.用条形图表示下表中关注不同广告的人数、频率。
广告类型
人数
比例
频率%
商品广告
112
0.560
56
服务广告
51
0.255
25.5
金融广告
9
0.045
4.5
房地产广告
16
0.080
8
招生招聘广告
10
0.050
5
其他广告
2
0.010
1
合计
200
1.000
100
5.从全校参加科技知识竞赛的学生试卷中,抽取一个样本,考察竞赛的成绩分布.将样本分成5组,绘成频率分布直方图(如图),图中从左到右各小组的小长方形的高的比是1∶3∶6∶4∶2,最后边一组的频数是6.请结合频率分布直方图提供的信息,解答下列问题:
(1)样本的容量是多少?
(2)列出频率分布表;
(3)成绩落在哪个范围内的人数最多 并求该小组的频数、频率;
(4)估计这次竞赛中,成绩不低于60分的学生占总人数的百分比.
B组
某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示,则其抽样的100根中,有____根在棉花纤维的长度小于20mm.
2.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图,如图,据图可得这100名学生中体重在[56.5,64.5)
kg的学生人数是(
)
A.
20
B
.30
C.
40
D
.50
3.为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
第二小组的频率是多少?样本容量是多少?
若次数在110以上(含110次)为达标,试估计
该学校全体高一学生的达标率是多少?
在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由。
1.5.1
估计总体的分布
答案
三、课前预习
1.频率分布是指一个样本数据在各个小范围内所占比例的大小。一般用频率分布直方图反映样本的频率分布。其一般步骤为:计算一组数据中最大值与最小值的差,即求极差(1)决定组距与组数;⑵将数据分组;⑶列频率分布表;⑷画频率分布直方图。
以课本P32106块头盖骨分布问题为例,经过以上几个步骤画出频率分布直方图。(让学生自己动手作图)
频率分布直方图的特征:⑴从频率分布直方图可以清楚的看出数据分布的总体趋势。⑵从频率分布直方图得不出原始的数据内容,把数据表示成直方图后,原有的具体数据信息就被抹掉了。
2.连接频率分布直方图中各小长方形上端的中点,就得到频率分布折线图。
四、堂中互动
解:(1)样本频率分布表如下:
(2)其频率分布直方图如下:
(3)由样本频率分布表可知身高小于134cm
的男孩出现的频率为0.04+0.07+0.08=0.19,所以我们估计身高小于134cm的人数占总人数的19%.
五、即学即练
1.
C
2.A
3.D
练案
A组
1.
60
2.B
3.A
4.解:人数分布条形图如下
频率分布条形图如下
5.解:(1)由于各组的组距相等,所以各组的频率与各小长方形的高成正比且各组频率的和等于1,那么各组的频率分别为,,,,.设该样本容量为n,则=,所以样本容量为n=48.
(2)由以上得频率分布表如下:
成绩
频数
频率
[50.5,60.5)
3
[60.5,70.5)
9
[70.5,80.5)
18
[80.5,90.5)
12
[90.5,100.5)
6
合计
48
1
(3)成绩落在[70.5,80.5)之间的人数最多,该组的频数和频率分别是18和.
(4)不低于60分的学生占总人数的百分比约为
×100%≈94%.
B组
1.35
2.A
3.分析:在频率分布直方图中,各小长方形的面积等于相应各组的频率,小长方形的高与频数成正比,各组频数之和等于样本容量,频率之和等于1。
解:(1)由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小,因此第二小组的频率为:又因为频率=
所以
(2)由图可估计该学校高一学生的达标率约为
(3)由已知可得各小组的频数依次为6,12,51,45,27,9,所以前三组的频数之和为69,前四组的频数之和为114,所以跳绳次数的中位数落在第四小组内。
0.5
人数(人)
时间(小时)
20
10
5
0
1.0
1.5
2.0
15
0.3
0.1
4.3
4.4
4.5
4.6
4.7
4.8
4.9
5.0
5.1
5.2
视力
90
100
110
120
130
140
150
次数
o
0.004
0.008
0.012
0.016
0.020
0.024
0.028
频率/组距
0.032
0.036
122
126
130
134
138
142
146
150
158
154
身高(cm)
o
0.01
0.02
0.03
0.04
0.05
0.06
0.07
频率/组距
