1.5.2 估计总体的数字特征 学案1(含答案)
文档属性
| 名称 | 1.5.2 估计总体的数字特征 学案1(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 157.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-16 19:02:17 | ||
图片预览




文档简介
1.5.2
估计总体的数字特征
学案
一、学习目标
1.了解众数、中位数、平均数并会求一组数据的平均数.
2.理解方差、标准差的概念并会求方差、标准差.
3.会用方差、标准差估计总体的数字特征.
4.形成对数据处理过程进行初步评价的意识.高
二、重点、难点
重点:用样本平均数和标准差估计总体的平均数与标准差.
难点:能应用相关知识解决简单的实际问题.
三、课前预习
(一)、众数、中位数、平均数
1.众数
一组数据中重复出现次数
的数称为这组数的众数.
2.
中位数把一组数据按从小到大的顺序排列,把处于最中间位置的那个数称为这组数据的中位数.
当数据个数为奇数时,中位数是按从小到大的顺序排列的
的那个数.
当数据个数为偶数时,中位数是按从小到大的顺序排列的最中间两个数的
.
3.
平均数
如果有n个数,那么
叫这n个数的平均数.
4.实际问题中求得的众数、中位数、平均数应带上单位.
(二)、标准差、方差
1.数据的离散程度可用极差、
、
来描述.样本方差描述了一组数据围绕平均数波动的大小.一般地,设样本的数据为,样本的平均数为,则定义
,表示方差.
2.为了得到以样本数据的单位表示的波动幅度,通常要求出样本方差的算术平方根
=
,表示样本标准差.不要漏写单位.
(三)、如何从频率分布直方图中估计众数、中位数、平均数呢?
众数:最高矩形的中点.
中位数:左右两边直方图的面积相等.
平均数:频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
四、堂中互动
【教师点拨】:对于中位数关键是把已知数据按顺序排列,当数据个数为奇数时,中位数是按从小到大的顺序排列的最中间的那个数.当数据个数为偶数时,中位数是按从小到大的顺序排列的最中间两个数的平均数.众数即找出现最多的数据,平均数只要按公式计算即可.
例1:据报道,某公司的33名职工的月工资(以元为单位)如下:
职务
董事长
副董事长
董事
总经理
经理
管理员
职员
人数
1
1
2
1
5
3
20
工资
5
500
5
000
3
500
3
000
2
500
2
000
1
500
(1)求该公司职工月工资的平均数、中位数、众数;
(2)假设副董事长的工资从5
000元提升到20
000元,董事长的工资从5
500元提升到30
000元,那么新的平均数、中位数、众数又是什么?(精确到元)
(3)你认为哪个统计量更能反映这个公司员工的工资水平?结合此问题谈一谈你的看法.
点评:熟练掌握平均数、中位数、众数定义及其计算公式.
【教师点拨】平均数是反映一组数据的平均水平,平均数越大,平均水平越高,平均数越小,平均水平越低;方差是反映一组数据的波动水平,方差越大,波动越大,越不稳定,方差越小,越稳定.
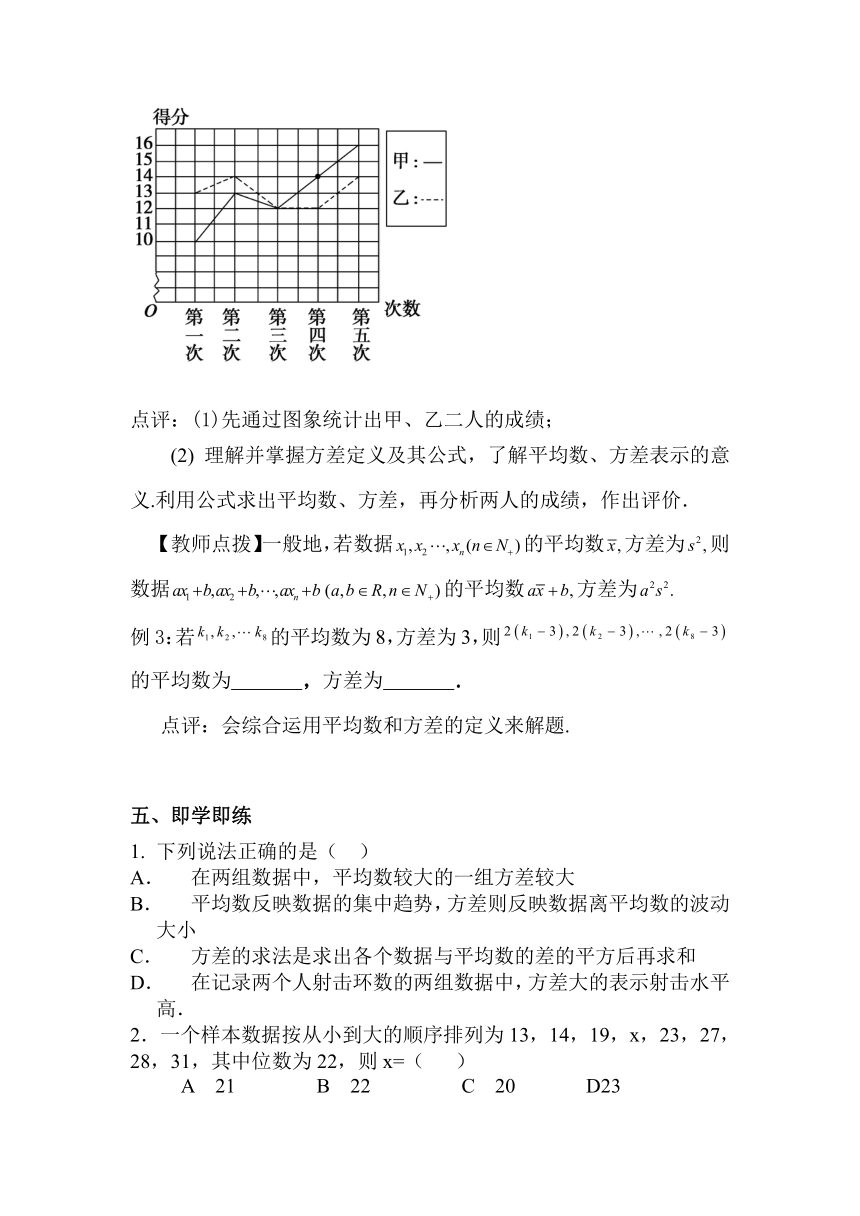
例2:甲乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图.
(1)分别求出两人得分的平均数与方差;
(2)根据图和上面算得的结果,对两人的训练成绩作出评价.
点评:(1)先通过图象统计出甲、乙二人的成绩;
(2)
理解并掌握方差定义及其公式,了解平均数、方差表示的意义.利用公式求出平均数、方差,再分析两人的成绩,作出评价.
【教师点拨】一般地,若数据的平均数方差为则数据的平均数方差为
例3:若的平均数为8,方差为3,则的平均数为
,方差为
.
点评:会综合运用平均数和方差的定义来解题.
五、即学即练
下列说法正确的是(
)
在两组数据中,平均数较大的一组方差较大
平均数反映数据的集中趋势,方差则反映数据离平均数的波动大小
方差的求法是求出各个数据与平均数的差的平方后再求和
在记录两个人射击环数的两组数据中,方差大的表示射击水平高.
2.一个样本数据按从小到大的顺序排列为13,14,19,x,23,27,28,31,其中位数为22,则x=(
)
A
21
B
22
C
20
D23
3.在某项体育比赛中,七位裁判为一选手打出的分数如下:
90
89
90
95
93
94
93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为(
)
A
92
,
2
B
92
,
2.8
C
93
,
2
D
93
,
2.8
4.样本101,98,102,100,99的标准差为(
)
A.
B.0
C.1
D.2
练案
A组
1.某人5次上班途中所花的时间(单位:min)分别为:x,y,10,11,9.已知这组数据的平均数是10,方差为2,则的值为(
)
A.1
B.2
C.3
D.4
2.
如图,样本A和B分别取自两个不同的总体,它们的样本平均数分别为,样本标准差分别为,则(
)
A
>,
B
<,
C
>,
D
<,高考资源
3.一个容量为40的样本数据依次为,若这个样本的标准差为,记,则
(
)
A.2
B.
C.
D.4
4.若数据这20个数据的平均数为;方差为0.20,则这21个数据的方差为
.
高
5.甲、乙、丙、丁四人参加射击项目选拔赛,成绩如下:
甲
乙
丙
丁
平均环数
8.5
8.8
8.8
8
方
差
3.5
3.5
2.1
8.7
则加奥运会的最佳人选是
.
6.从A、B两种棉花中各抽10株,测得它们的株高如下:(CM)
A、
25
41
40
37
22
14
19
39
21
42
B、
27
16
44
27
44
16
40
16
40
40
(1)
哪种棉花的苗长得高?
(2)
哪种棉花的苗长得整齐?
7.鱼塘里放养鱼苗4万条,根据近几年的经验知道,鱼苗成活率为95%,一段时间后准备打捞出售.第一次网出40条,称得平均每条鱼重2.2
kg;第二次网出25条,称得平均每条鱼重2.5
kg;第三次网出35条,称得平均每条鱼重2.8
kg.
(1)根据上述数据,估计鱼塘中鱼的总重量大约是多少;
(2)如果把整塘鱼全部售出,按市场价每千克10元计算,那么能收入多少元 除去成本80万元,纯收入是多少元
B组
1.若的方差为3,则的方差为.
2.在一次歌手大奖赛上,七位评委为歌手打出的分数如下:,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为(
)
A.
B.
C.
D.
3.
从甲乙两个总体中各抽取了一个样本:
甲
6
5
8
4
9
6
乙
8
7
6
5
8
2
根据以上数据,说明哪个波动小?
4..从高三抽出50名学生参加数学竞赛,由成绩得到如图的频率分布直方图.由于一些数据丢失,试利用频率分布直方图求:
(1)这50名学生成绩的众数与中位数.
(2)这50名学生的平均成绩.
1.5.2
估计总体的数字特征
答案
课前预习(一)
最多
(1)最中间
(2)平均数
(二)
1.标准差、方差
2.
四、堂中互动
例1.【解析】:(1)平均数是
=1
500+
≈1
500+591=2
091(元).
中位数是1
500元,众数是1
500元.
(2)平均数是
≈1
500+1
788=3
288(元).
中位数是1
500元,众数是1
500元.
(3)在这个问题中,中位数或众数均能反映该公司员工的工资水平.因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数与中位数偏差较大,所以平均数不能反映这个公司员工的工资水平.
【反思】:在用平均数估计总体的时候,样本中的每一个数据都会影响到平均数的大小,因此在实际操作中,一定要注意个别极端值对平均数的影响.
例2.【解析】:解 (1)由图象可得甲、乙两人五次测试的成绩分别为
甲:10分,13分,12分,14分,16分;
乙:13分,14分,12分,12分,14分.中学21世纪教育网21世纪教育网==13(分),==13(分),
=[(10-13)2+(13-13)2+(12-13)2+(14-13)2+(16-13)2]=4(分),
=[(13-13)2+(14-13)2+(12-13)2+(12-13)2+(14-13)2]=0.8(分).
(2)由可知乙的成绩较稳定.从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,可知甲的成绩在不断提高,而乙的成绩则无明显提高.
【反思】:一组数据的方差,刻画了这组数据的波动大小(即各数据偏离平均数的大小,也称离散性、差异性).方差越大,说明这组数据的波动越大,即这组数据越分散;方差越小,说明这组数据越集中.
例3.【解析】:(1)因为的平均数为,
的平均数为
,
(2)因为得方差为3,即
所以的方差高考
【反思】:若的平均数为,方差为,则
的平均数为,方差为,标准差为.
五、即学即练
1.B
2.A
3.B
4.A
练案
A组
1.D
2.B
3.
A
4.
5.
丙
6.乙种棉花的苗长得高,甲种棉花的苗长得整齐。
7.
所以鱼塘中鱼的总重量约为2.53×(40
000×95%)=96140(kg).即鱼塘中鱼的总重量大约是96140
kg.
(2)10×96140=961400(元),961400-800000=161400(元),
所以把整塘鱼全部售出能收入961400元,纯收入是161400元.
练案
B组
1.12
2.
D
3.甲波动小
4.解析:(1)由众数的概念可知,众数是出现次数最多的数.在直方图中高度最高的小长方形框的中间值的横坐标即为所求,所以众数应为75.
由于中位数是所有数据中的中间值,故在频率分布直方图中体现的是中位数的左右两边频数应相等,即频率也相等,从而就是小矩形的面积和相等.因此在频率分布直方图中将频率分布直方图中所有小矩形的面积一分为二的直线所对应的成绩即为所求.
∵0.004×10+0.006×10+0.02×10=0.04+0.06+0.2=0.3,
∴前三个小矩形面积的和为0.3.
而第四个小矩形面积为0.03×10=0.3,0.3+0.3>0.5,
∴中位数应位于第四个小矩形内.
设其底边为x,高为0.03,令0.03x=0.2,得x≈6.7,
故中位数应为70+6.7=76.7
(2)样本平均数应是频率分布直方图的“重心”,即所有数据的平均值,取每个小矩形底边的中点值乘以每个小矩形的面积即可.
∴平均成绩为45×(0.004×10)+55×(0.006×10)+65×(0.02×10)+75×(0.03×10)+85×(0.021×10)+95×(0.016×10)≈74,
∴众数是75,中位数约为77,平均成绩约为74.
估计总体的数字特征
学案
一、学习目标
1.了解众数、中位数、平均数并会求一组数据的平均数.
2.理解方差、标准差的概念并会求方差、标准差.
3.会用方差、标准差估计总体的数字特征.
4.形成对数据处理过程进行初步评价的意识.高
二、重点、难点
重点:用样本平均数和标准差估计总体的平均数与标准差.
难点:能应用相关知识解决简单的实际问题.
三、课前预习
(一)、众数、中位数、平均数
1.众数
一组数据中重复出现次数
的数称为这组数的众数.
2.
中位数把一组数据按从小到大的顺序排列,把处于最中间位置的那个数称为这组数据的中位数.
当数据个数为奇数时,中位数是按从小到大的顺序排列的
的那个数.
当数据个数为偶数时,中位数是按从小到大的顺序排列的最中间两个数的
.
3.
平均数
如果有n个数,那么
叫这n个数的平均数.
4.实际问题中求得的众数、中位数、平均数应带上单位.
(二)、标准差、方差
1.数据的离散程度可用极差、
、
来描述.样本方差描述了一组数据围绕平均数波动的大小.一般地,设样本的数据为,样本的平均数为,则定义
,表示方差.
2.为了得到以样本数据的单位表示的波动幅度,通常要求出样本方差的算术平方根
=
,表示样本标准差.不要漏写单位.
(三)、如何从频率分布直方图中估计众数、中位数、平均数呢?
众数:最高矩形的中点.
中位数:左右两边直方图的面积相等.
平均数:频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
四、堂中互动
【教师点拨】:对于中位数关键是把已知数据按顺序排列,当数据个数为奇数时,中位数是按从小到大的顺序排列的最中间的那个数.当数据个数为偶数时,中位数是按从小到大的顺序排列的最中间两个数的平均数.众数即找出现最多的数据,平均数只要按公式计算即可.
例1:据报道,某公司的33名职工的月工资(以元为单位)如下:
职务
董事长
副董事长
董事
总经理
经理
管理员
职员
人数
1
1
2
1
5
3
20
工资
5
500
5
000
3
500
3
000
2
500
2
000
1
500
(1)求该公司职工月工资的平均数、中位数、众数;
(2)假设副董事长的工资从5
000元提升到20
000元,董事长的工资从5
500元提升到30
000元,那么新的平均数、中位数、众数又是什么?(精确到元)
(3)你认为哪个统计量更能反映这个公司员工的工资水平?结合此问题谈一谈你的看法.
点评:熟练掌握平均数、中位数、众数定义及其计算公式.
【教师点拨】平均数是反映一组数据的平均水平,平均数越大,平均水平越高,平均数越小,平均水平越低;方差是反映一组数据的波动水平,方差越大,波动越大,越不稳定,方差越小,越稳定.
例2:甲乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图.
(1)分别求出两人得分的平均数与方差;
(2)根据图和上面算得的结果,对两人的训练成绩作出评价.
点评:(1)先通过图象统计出甲、乙二人的成绩;
(2)
理解并掌握方差定义及其公式,了解平均数、方差表示的意义.利用公式求出平均数、方差,再分析两人的成绩,作出评价.
【教师点拨】一般地,若数据的平均数方差为则数据的平均数方差为
例3:若的平均数为8,方差为3,则的平均数为
,方差为
.
点评:会综合运用平均数和方差的定义来解题.
五、即学即练
下列说法正确的是(
)
在两组数据中,平均数较大的一组方差较大
平均数反映数据的集中趋势,方差则反映数据离平均数的波动大小
方差的求法是求出各个数据与平均数的差的平方后再求和
在记录两个人射击环数的两组数据中,方差大的表示射击水平高.
2.一个样本数据按从小到大的顺序排列为13,14,19,x,23,27,28,31,其中位数为22,则x=(
)
A
21
B
22
C
20
D23
3.在某项体育比赛中,七位裁判为一选手打出的分数如下:
90
89
90
95
93
94
93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为(
)
A
92
,
2
B
92
,
2.8
C
93
,
2
D
93
,
2.8
4.样本101,98,102,100,99的标准差为(
)
A.
B.0
C.1
D.2
练案
A组
1.某人5次上班途中所花的时间(单位:min)分别为:x,y,10,11,9.已知这组数据的平均数是10,方差为2,则的值为(
)
A.1
B.2
C.3
D.4
2.
如图,样本A和B分别取自两个不同的总体,它们的样本平均数分别为,样本标准差分别为,则(
)
A
>,
B
<,
C
>,
D
<,高考资源
3.一个容量为40的样本数据依次为,若这个样本的标准差为,记,则
(
)
A.2
B.
C.
D.4
4.若数据这20个数据的平均数为;方差为0.20,则这21个数据的方差为
.
高
5.甲、乙、丙、丁四人参加射击项目选拔赛,成绩如下:
甲
乙
丙
丁
平均环数
8.5
8.8
8.8
8
方
差
3.5
3.5
2.1
8.7
则加奥运会的最佳人选是
.
6.从A、B两种棉花中各抽10株,测得它们的株高如下:(CM)
A、
25
41
40
37
22
14
19
39
21
42
B、
27
16
44
27
44
16
40
16
40
40
(1)
哪种棉花的苗长得高?
(2)
哪种棉花的苗长得整齐?
7.鱼塘里放养鱼苗4万条,根据近几年的经验知道,鱼苗成活率为95%,一段时间后准备打捞出售.第一次网出40条,称得平均每条鱼重2.2
kg;第二次网出25条,称得平均每条鱼重2.5
kg;第三次网出35条,称得平均每条鱼重2.8
kg.
(1)根据上述数据,估计鱼塘中鱼的总重量大约是多少;
(2)如果把整塘鱼全部售出,按市场价每千克10元计算,那么能收入多少元 除去成本80万元,纯收入是多少元
B组
1.若的方差为3,则的方差为.
2.在一次歌手大奖赛上,七位评委为歌手打出的分数如下:,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为(
)
A.
B.
C.
D.
3.
从甲乙两个总体中各抽取了一个样本:
甲
6
5
8
4
9
6
乙
8
7
6
5
8
2
根据以上数据,说明哪个波动小?
4..从高三抽出50名学生参加数学竞赛,由成绩得到如图的频率分布直方图.由于一些数据丢失,试利用频率分布直方图求:
(1)这50名学生成绩的众数与中位数.
(2)这50名学生的平均成绩.
1.5.2
估计总体的数字特征
答案
课前预习(一)
最多
(1)最中间
(2)平均数
(二)
1.标准差、方差
2.
四、堂中互动
例1.【解析】:(1)平均数是
=1
500+
≈1
500+591=2
091(元).
中位数是1
500元,众数是1
500元.
(2)平均数是
≈1
500+1
788=3
288(元).
中位数是1
500元,众数是1
500元.
(3)在这个问题中,中位数或众数均能反映该公司员工的工资水平.因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数与中位数偏差较大,所以平均数不能反映这个公司员工的工资水平.
【反思】:在用平均数估计总体的时候,样本中的每一个数据都会影响到平均数的大小,因此在实际操作中,一定要注意个别极端值对平均数的影响.
例2.【解析】:解 (1)由图象可得甲、乙两人五次测试的成绩分别为
甲:10分,13分,12分,14分,16分;
乙:13分,14分,12分,12分,14分.中学21世纪教育网21世纪教育网==13(分),==13(分),
=[(10-13)2+(13-13)2+(12-13)2+(14-13)2+(16-13)2]=4(分),
=[(13-13)2+(14-13)2+(12-13)2+(12-13)2+(14-13)2]=0.8(分).
(2)由可知乙的成绩较稳定.从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,可知甲的成绩在不断提高,而乙的成绩则无明显提高.
【反思】:一组数据的方差,刻画了这组数据的波动大小(即各数据偏离平均数的大小,也称离散性、差异性).方差越大,说明这组数据的波动越大,即这组数据越分散;方差越小,说明这组数据越集中.
例3.【解析】:(1)因为的平均数为,
的平均数为
,
(2)因为得方差为3,即
所以的方差高考
【反思】:若的平均数为,方差为,则
的平均数为,方差为,标准差为.
五、即学即练
1.B
2.A
3.B
4.A
练案
A组
1.D
2.B
3.
A
4.
5.
丙
6.乙种棉花的苗长得高,甲种棉花的苗长得整齐。
7.
所以鱼塘中鱼的总重量约为2.53×(40
000×95%)=96140(kg).即鱼塘中鱼的总重量大约是96140
kg.
(2)10×96140=961400(元),961400-800000=161400(元),
所以把整塘鱼全部售出能收入961400元,纯收入是161400元.
练案
B组
1.12
2.
D
3.甲波动小
4.解析:(1)由众数的概念可知,众数是出现次数最多的数.在直方图中高度最高的小长方形框的中间值的横坐标即为所求,所以众数应为75.
由于中位数是所有数据中的中间值,故在频率分布直方图中体现的是中位数的左右两边频数应相等,即频率也相等,从而就是小矩形的面积和相等.因此在频率分布直方图中将频率分布直方图中所有小矩形的面积一分为二的直线所对应的成绩即为所求.
∵0.004×10+0.006×10+0.02×10=0.04+0.06+0.2=0.3,
∴前三个小矩形面积的和为0.3.
而第四个小矩形面积为0.03×10=0.3,0.3+0.3>0.5,
∴中位数应位于第四个小矩形内.
设其底边为x,高为0.03,令0.03x=0.2,得x≈6.7,
故中位数应为70+6.7=76.7
(2)样本平均数应是频率分布直方图的“重心”,即所有数据的平均值,取每个小矩形底边的中点值乘以每个小矩形的面积即可.
∴平均成绩为45×(0.004×10)+55×(0.006×10)+65×(0.02×10)+75×(0.03×10)+85×(0.021×10)+95×(0.016×10)≈74,
∴众数是75,中位数约为77,平均成绩约为74.
