1.6 统计活动结婚年龄的变化 同步测试(含答案)
文档属性
| 名称 | 1.6 统计活动结婚年龄的变化 同步测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 230.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-16 00:00:00 | ||
图片预览



文档简介
1.6
统计活动:结婚年龄的变化
同步测试
一、选择题(每小题4分,共16分)
1.(2014·青岛高一检测)为了调查某市高中学生中喜欢数学的同学所占的比例,收集数据后,整理数据的方式是 ( )
A.频率分布直方图
B.茎叶图
C.计算平均数和标准差
D.扇形统计图
【解析】选D.扇形统计图能清楚地表示出各部分在总体中所占的比例.
2.下列统计活动中,不适宜用问卷调查的是 ( )
A.某中学高一年级一班学生每晚的睡眠时间
B.某校要了解在校教师的年龄状况
C.某市场要了解居民的环保意识
D.了解某地甜瓜的甜度和含水量
【解析】选D.A.人数不多,容易调查,因而适宜用问卷调查.
B.人数不多,容易调查,结果好统计,因而适宜用问卷调查.
C.环保意识可以通过设计问题来调查,因而适宜用问卷调查.
D.甜度和含水量不是每个人都可以了解的,因而不适宜用问卷调查,故应选此项.
3.(2014·郑州高一检测)对于下列调查,比较适合用普查方法的是 ( )
A.调查某种产品的知名度
B.调查央视春节晚会的全国收视率
C.检验一批弹药的爆炸威力
D.调查某居民楼10户居民的月平均用电量
【解析】选D.A,B中,调查央视春节晚会的全国收视率情况以及调查某种产品的知名度情况,范围比较大,普查的意义或价值不大,应选择抽样调查,故选项A,B错误;
C中,调查一批弹药的爆炸威力具有破坏性,适合用抽样调查,故选项C错误;
D中,调查某居民楼10户居民的月平均用电量情况,适合普查,故此选项正确.
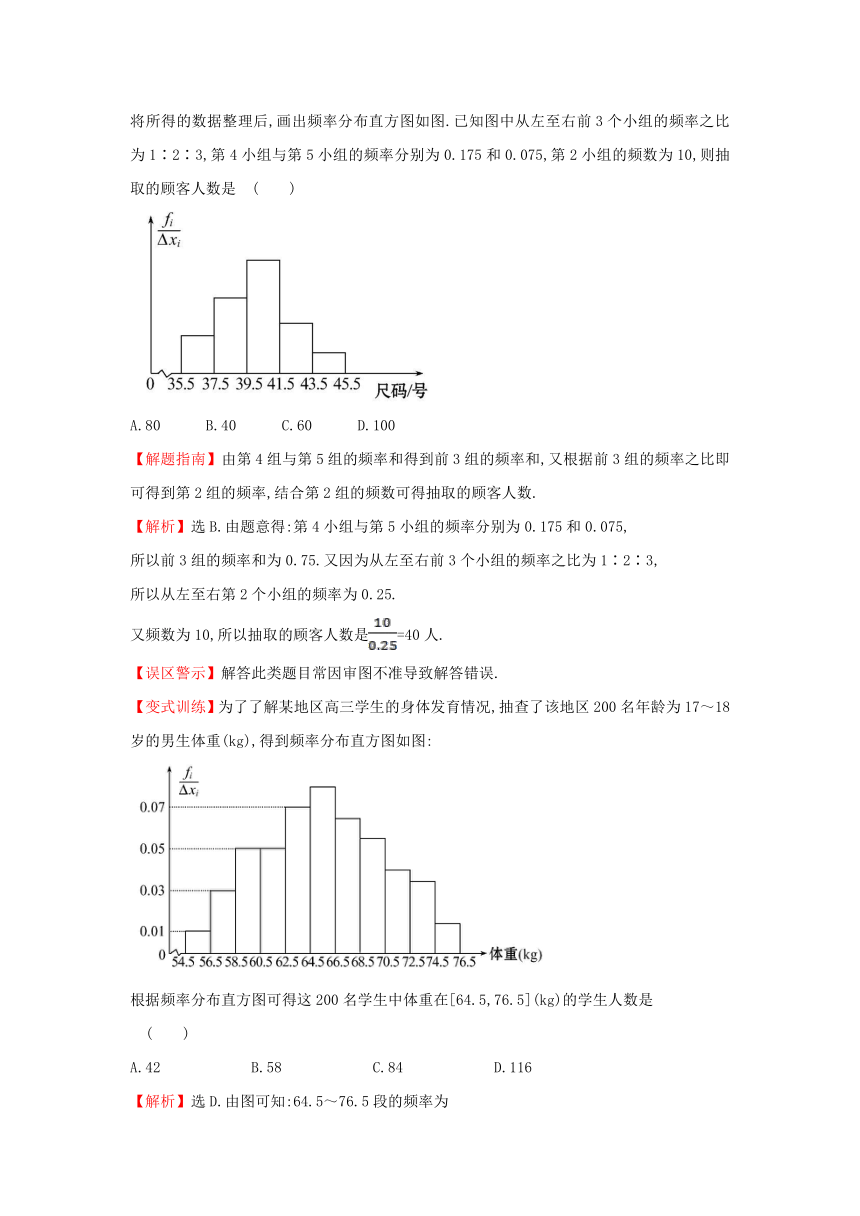
4.(2014·枣庄高一检测)为了了解商场某日旅游鞋的销售情况,抽取了部分顾客购鞋的尺寸,将所得的数据整理后,画出频率分布直方图如图.已知图中从左至右前3个小组的频率之比为1∶2∶3,第4小组与第5小组的频率分别为0.175和0.075,第2小组的频数为10,则抽取的顾客人数是 ( )
A.80 B.40 C.60 D.100
【解题指南】由第4组与第5组的频率和得到前3组的频率和,又根据前3组的频率之比即可得到第2组的频率,结合第2组的频数可得抽取的顾客人数.
【解析】选B.由题意得:第4小组与第5小组的频率分别为0.175和0.075,
所以前3组的频率和为0.75.又因为从左至右前3个小组的频率之比为1∶2∶3,
所以从左至右第2个小组的频率为0.25.
又频数为10,所以抽取的顾客人数是=40人.
【误区警示】解答此类题目常因审图不准导致解答错误.
【变式训练】为了了解某地区高三学生的身体发育情况,抽查了该地区200名年龄为17~18岁的男生体重(kg),得到频率分布直方图如图:
根据频率分布直方图可得这200名学生中体重在[64.5,76.5](kg)的学生人数是
( )
A.42
B.58
C.84
D.116
【解析】选D.由图可知:64.5~76.5段的频率为
1-(0.01+0.03+0.05×2+0.07)×2=0.58,
则频数为200×0.58=116人.
二、填空题(每小题5分,共10分)
5.已知10个数如下:63,65,67,69,66,64,66,64,65,68,对这些数据绘制频率分布直方图,其中一组[64.5,66.5]的小矩形的高是__________.
【解析】根据已知的一组的区间[64.5,66.5]可知,分组的组距是2,此组的频数是4,
所以频率是0.4,所以表示这一组小矩形的高是=0.2.
答案:0.2
【举一反三】在本题中,区间[66.5,68.5]上矩形高度是多少
【解析】频数为2,频率为0.2,组距为2,矩形高度为:=0.1.
6.某校高一年级一班班长统计去年1~8月“校园文化”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,这组数据的中位数是________.
【解析】这组数据从小到大为:28,36,42,58,58,70,75,83,故这组数据的中位数为=58.
答案:58
三、解答题(每小题12分,共24分)
7.(2014·西安高一检测)某中学部分学生参加全国高中数学竞赛,取得了优异成绩,指导老师统计了所有参赛同学的成绩(成绩都为整数,试题满分120分),并且绘制了“频数分布图”,请回答:
(1)该中学参加本次数学竞赛的有多少人
(2)如果90分以上(含90分)获奖,那么获奖率是多少
(3)这次竞赛成绩的中位数落在哪段内
(4)图中还提供了其他信息,再写出两条.
【解析】(1)由分布图可知,4+6+8+7+5+2=32(人).
(2)90分以上(含90分)的人数为7+5+2=14(人),
所以×100%=43.75%.
(3)参赛同学共有32人.按成绩排序后,第16,17个是最中间的两个.而第16个和第17个都落在80~90分,
所以这次竞赛成绩的中位数落在80~90分内.
(4)①落在80~90分数段内的人数最多,有8人;
②参赛同学成绩均不低于60分.
8.某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名学生进行调查,下表是这n名学生的日睡眠时间的频率分布表.
分组(睡眠时间)
频数(人数)
频率
[4.5,5.5)
5
0.10
[5.5,6.5)
0.20
[6.5,7.5)
a
[7.5,8.5)
b
[8.5,9.5]
0.10
(1)求n的值.若a=20,将表中数据补全,并画出频率分布直方图.
(2)统计方法中,同一组数据常用该组区间的中点值(例如,区间[4.5,5.5)的中点值是5)作为代表.若据此计算的上述数据的平均值为7.2,求a,b的值,并由此估计该学校学生的日平均睡眠时间在7.5h以上的概率.
【解析】(1)由表可得,=0.10,所以n=50.当a=20时,补全的频率分布表如下:
分组(睡眠时间)
频数(人数)
频率
[4.5,5.5)
5
0.10
[5.5,6.5)
10
0.20
[6.5,7.5)
20
0.40
[7.
5,8.5)
10
0.20
[8.5,9.5]
5
0.10
频率分布直方图为:
(2)根据题意得(5×5+6×10+7×a+8×b+9×5)÷50=7.2,化简得7a+8b=230 ①
又因为样本容量n=50,
所以5+0.20×50+a+b+0.10×50=50,
即a+b=30 ②
由①②解得a=10,b=20.由此估计该学校学生的日平均睡眠时间在7.5h以上的概率是=0.50.
一、选择题(每小题4分,共12分)
1.(2014·佛山高一检测)吸烟有害健康,被动吸烟也有害健康,如果要了解人们被动吸烟的情况,则最合适的调查方式是 ( )
A.普查
B.抽样调查
C.在社会上随机调查
D.在学校里随机调查
【解析】选B.要了解人们被动吸烟的情况,由于人数众多,意义不大,选普查不合适,在社会上和在学校里随机调查,选择的对象不全面,故应抽样调查,故选B.
2.下面是四位同学对他们学习小组将要共同进行的一次统计活动分别设计的活动程序,其中正确的是 ( )
【解题指南】根据统计调查的步骤即可设计成C的方案.数据处理应该是属于整理数据,数据表示应该属于描述数据.
【解析】选C.统计调查一般分为以下几步:收集数据、整理数据、描述数据、分析数据.
【变式训练】在统计中,样本的标准差可以近似地反映总体的 ( )
A.平均状态
B.分布规律
C.波动大小
D.最大值与最小值
【解析】选C.样本的标准差和方差反映样本数据的波动大小及离散程度.
3.(2014·蚌埠高一检测)某次统计活动得到的结论与实际有较大差别,其原因可能是 ( )
A.调查方式不科学
B.没有选用合适的分析数据的方法
C.确定的调查对象不合要求
D.以上都有可能
【解析】选D.结论与实际相差较大原因是多方面的,调查方式不科学,没有选用合适的分析数据的方法,确定的调查对象不合要求,这些原因都有可能.故选D.
二、填空题(每小题4分,共8分)
4.(2014·汉中高一检测)为了开展“家电下乡”活动,政府调查某地区家庭拥有彩电的情况,从该地区的10万户居民中,随机抽查了96户,这96户拥有彩电的情况如下:
彩色电视机
集镇(户)
农村(户)
有
36
42
无
4
14
若该地区集镇与农村住户之比为3∶5,估计该地区家庭中没有彩色电视机的总户数为__________.
【解析】样本中农村没有彩电的比例为P=×100%=25%,集镇中没有彩电的比例为Q=×100%=10%,则该地区没有彩电的总户数约为105××25%+105××10%=15625+3750=19375(户).
答案:19375
【举一反三】本题中若用扇形图表示该地区有无彩色电视机住户,那么无彩色电视机的扇形区域对应的比例是多少
【解析】=0.19375=19.375%.
5.(2013·宜春高二检测)为了解某县2013年初中毕业生数学质量检测成绩等级的分布情况,随机抽取了该县若干名初中毕业生的数学质量检测成绩,按A,B,C,D四个等级进行统计分析,并绘制了如图所示的统计图:
请根据以上统计图提供的信息,解答下列问题:
(1)本次抽取的学生有________名.
(2)在抽取的学生中,C级人数所占的百分比是______.
(3)根据抽样调查结果,2013年该县1430名初中毕业生数学质量检测成绩为A级的人数为________人.
【解析】(1)20÷20%=100(名).
(2)×100%=30%.
(3)1430×20%=286(人).
答案:(1)100 (2)30% (3)286
三、解答题(每小题10分,共20分)
6.如图所示,报纸上一则广告绘制了如图的统计图,并称“乙品牌牛奶每天的销售量是甲品牌牛奶每天销售量的3倍”.请分析这则广告信息正确吗
【解析】这则广告的宣传是不正确的.从图中标明的数据看,甲品牌牛奶每天的销售量是510万袋,乙品牌牛奶每天的销售量是530万袋,只比甲品牌牛奶多了20万袋.乙品牌牛奶的销售量并不是甲品牌牛奶销售量的3倍.由于统计图制作的不规范,容易误导消费者认为乙品牌牛奶的销售量是甲品牌牛奶销售量的3倍.这则广告信息是不正确的.
【拓展延伸】作出决策的策略
实际问题要先选用有代表性的数据,然后通过整理数据,选用多种方式分析数据,作出正确、合理的决策.
7.(2014·大连高一检测)在一次人才招聘会上,有一家公司的招聘员说:“我们公司的收入水平很高,去年,在50名员工中,最高年收入达到了100万,他们年收入的平均数是3.5万.”
(1)你是否能够判断自己可以成为此公司的一名高收入者
(2)如果招聘员继续告诉你:“员工收入的变化范围是从0.5万到100万,”这个信息是否足以使你作出自己是否受聘的决定 为什么
(3)如果招聘员继续给你提供如下信息,员工收入的中间50%(即去掉最少的25%和最多的25%后所剩下的)的变化范围是1万到3万,你又该如何使用这条信息来作出是否受聘的决定
(4)为什么平均数比中间50%高很多 你能估计出收入的中位数是多少吗
【解析】(1)由于年收入的平均数是3.5万与最高年收入100万相差太大,所以不能判断一定能成为此公司的一名高收入者.
(2)由题可知员工收入的变化范围及平均数,高收入者只是极少数,所以不能作出是否受聘的决定.
(3)大部分员工的收入是1万到3万,这也是受聘该公司后最有可能的收入状况,所以这可以作出是否受聘的决定.
(4)收入极高的少数人对平均数影响较大,他们的收入与平均数相差太多.由于员工收入的中间50%的变化范围是1万到3万,可以估计收入的中位数大约是=2(万元).
统计活动:结婚年龄的变化
同步测试
一、选择题(每小题4分,共16分)
1.(2014·青岛高一检测)为了调查某市高中学生中喜欢数学的同学所占的比例,收集数据后,整理数据的方式是 ( )
A.频率分布直方图
B.茎叶图
C.计算平均数和标准差
D.扇形统计图
【解析】选D.扇形统计图能清楚地表示出各部分在总体中所占的比例.
2.下列统计活动中,不适宜用问卷调查的是 ( )
A.某中学高一年级一班学生每晚的睡眠时间
B.某校要了解在校教师的年龄状况
C.某市场要了解居民的环保意识
D.了解某地甜瓜的甜度和含水量
【解析】选D.A.人数不多,容易调查,因而适宜用问卷调查.
B.人数不多,容易调查,结果好统计,因而适宜用问卷调查.
C.环保意识可以通过设计问题来调查,因而适宜用问卷调查.
D.甜度和含水量不是每个人都可以了解的,因而不适宜用问卷调查,故应选此项.
3.(2014·郑州高一检测)对于下列调查,比较适合用普查方法的是 ( )
A.调查某种产品的知名度
B.调查央视春节晚会的全国收视率
C.检验一批弹药的爆炸威力
D.调查某居民楼10户居民的月平均用电量
【解析】选D.A,B中,调查央视春节晚会的全国收视率情况以及调查某种产品的知名度情况,范围比较大,普查的意义或价值不大,应选择抽样调查,故选项A,B错误;
C中,调查一批弹药的爆炸威力具有破坏性,适合用抽样调查,故选项C错误;
D中,调查某居民楼10户居民的月平均用电量情况,适合普查,故此选项正确.
4.(2014·枣庄高一检测)为了了解商场某日旅游鞋的销售情况,抽取了部分顾客购鞋的尺寸,将所得的数据整理后,画出频率分布直方图如图.已知图中从左至右前3个小组的频率之比为1∶2∶3,第4小组与第5小组的频率分别为0.175和0.075,第2小组的频数为10,则抽取的顾客人数是 ( )
A.80 B.40 C.60 D.100
【解题指南】由第4组与第5组的频率和得到前3组的频率和,又根据前3组的频率之比即可得到第2组的频率,结合第2组的频数可得抽取的顾客人数.
【解析】选B.由题意得:第4小组与第5小组的频率分别为0.175和0.075,
所以前3组的频率和为0.75.又因为从左至右前3个小组的频率之比为1∶2∶3,
所以从左至右第2个小组的频率为0.25.
又频数为10,所以抽取的顾客人数是=40人.
【误区警示】解答此类题目常因审图不准导致解答错误.
【变式训练】为了了解某地区高三学生的身体发育情况,抽查了该地区200名年龄为17~18岁的男生体重(kg),得到频率分布直方图如图:
根据频率分布直方图可得这200名学生中体重在[64.5,76.5](kg)的学生人数是
( )
A.42
B.58
C.84
D.116
【解析】选D.由图可知:64.5~76.5段的频率为
1-(0.01+0.03+0.05×2+0.07)×2=0.58,
则频数为200×0.58=116人.
二、填空题(每小题5分,共10分)
5.已知10个数如下:63,65,67,69,66,64,66,64,65,68,对这些数据绘制频率分布直方图,其中一组[64.5,66.5]的小矩形的高是__________.
【解析】根据已知的一组的区间[64.5,66.5]可知,分组的组距是2,此组的频数是4,
所以频率是0.4,所以表示这一组小矩形的高是=0.2.
答案:0.2
【举一反三】在本题中,区间[66.5,68.5]上矩形高度是多少
【解析】频数为2,频率为0.2,组距为2,矩形高度为:=0.1.
6.某校高一年级一班班长统计去年1~8月“校园文化”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,这组数据的中位数是________.
【解析】这组数据从小到大为:28,36,42,58,58,70,75,83,故这组数据的中位数为=58.
答案:58
三、解答题(每小题12分,共24分)
7.(2014·西安高一检测)某中学部分学生参加全国高中数学竞赛,取得了优异成绩,指导老师统计了所有参赛同学的成绩(成绩都为整数,试题满分120分),并且绘制了“频数分布图”,请回答:
(1)该中学参加本次数学竞赛的有多少人
(2)如果90分以上(含90分)获奖,那么获奖率是多少
(3)这次竞赛成绩的中位数落在哪段内
(4)图中还提供了其他信息,再写出两条.
【解析】(1)由分布图可知,4+6+8+7+5+2=32(人).
(2)90分以上(含90分)的人数为7+5+2=14(人),
所以×100%=43.75%.
(3)参赛同学共有32人.按成绩排序后,第16,17个是最中间的两个.而第16个和第17个都落在80~90分,
所以这次竞赛成绩的中位数落在80~90分内.
(4)①落在80~90分数段内的人数最多,有8人;
②参赛同学成绩均不低于60分.
8.某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名学生进行调查,下表是这n名学生的日睡眠时间的频率分布表.
分组(睡眠时间)
频数(人数)
频率
[4.5,5.5)
5
0.10
[5.5,6.5)
0.20
[6.5,7.5)
a
[7.5,8.5)
b
[8.5,9.5]
0.10
(1)求n的值.若a=20,将表中数据补全,并画出频率分布直方图.
(2)统计方法中,同一组数据常用该组区间的中点值(例如,区间[4.5,5.5)的中点值是5)作为代表.若据此计算的上述数据的平均值为7.2,求a,b的值,并由此估计该学校学生的日平均睡眠时间在7.5h以上的概率.
【解析】(1)由表可得,=0.10,所以n=50.当a=20时,补全的频率分布表如下:
分组(睡眠时间)
频数(人数)
频率
[4.5,5.5)
5
0.10
[5.5,6.5)
10
0.20
[6.5,7.5)
20
0.40
[7.
5,8.5)
10
0.20
[8.5,9.5]
5
0.10
频率分布直方图为:
(2)根据题意得(5×5+6×10+7×a+8×b+9×5)÷50=7.2,化简得7a+8b=230 ①
又因为样本容量n=50,
所以5+0.20×50+a+b+0.10×50=50,
即a+b=30 ②
由①②解得a=10,b=20.由此估计该学校学生的日平均睡眠时间在7.5h以上的概率是=0.50.
一、选择题(每小题4分,共12分)
1.(2014·佛山高一检测)吸烟有害健康,被动吸烟也有害健康,如果要了解人们被动吸烟的情况,则最合适的调查方式是 ( )
A.普查
B.抽样调查
C.在社会上随机调查
D.在学校里随机调查
【解析】选B.要了解人们被动吸烟的情况,由于人数众多,意义不大,选普查不合适,在社会上和在学校里随机调查,选择的对象不全面,故应抽样调查,故选B.
2.下面是四位同学对他们学习小组将要共同进行的一次统计活动分别设计的活动程序,其中正确的是 ( )
【解题指南】根据统计调查的步骤即可设计成C的方案.数据处理应该是属于整理数据,数据表示应该属于描述数据.
【解析】选C.统计调查一般分为以下几步:收集数据、整理数据、描述数据、分析数据.
【变式训练】在统计中,样本的标准差可以近似地反映总体的 ( )
A.平均状态
B.分布规律
C.波动大小
D.最大值与最小值
【解析】选C.样本的标准差和方差反映样本数据的波动大小及离散程度.
3.(2014·蚌埠高一检测)某次统计活动得到的结论与实际有较大差别,其原因可能是 ( )
A.调查方式不科学
B.没有选用合适的分析数据的方法
C.确定的调查对象不合要求
D.以上都有可能
【解析】选D.结论与实际相差较大原因是多方面的,调查方式不科学,没有选用合适的分析数据的方法,确定的调查对象不合要求,这些原因都有可能.故选D.
二、填空题(每小题4分,共8分)
4.(2014·汉中高一检测)为了开展“家电下乡”活动,政府调查某地区家庭拥有彩电的情况,从该地区的10万户居民中,随机抽查了96户,这96户拥有彩电的情况如下:
彩色电视机
集镇(户)
农村(户)
有
36
42
无
4
14
若该地区集镇与农村住户之比为3∶5,估计该地区家庭中没有彩色电视机的总户数为__________.
【解析】样本中农村没有彩电的比例为P=×100%=25%,集镇中没有彩电的比例为Q=×100%=10%,则该地区没有彩电的总户数约为105××25%+105××10%=15625+3750=19375(户).
答案:19375
【举一反三】本题中若用扇形图表示该地区有无彩色电视机住户,那么无彩色电视机的扇形区域对应的比例是多少
【解析】=0.19375=19.375%.
5.(2013·宜春高二检测)为了解某县2013年初中毕业生数学质量检测成绩等级的分布情况,随机抽取了该县若干名初中毕业生的数学质量检测成绩,按A,B,C,D四个等级进行统计分析,并绘制了如图所示的统计图:
请根据以上统计图提供的信息,解答下列问题:
(1)本次抽取的学生有________名.
(2)在抽取的学生中,C级人数所占的百分比是______.
(3)根据抽样调查结果,2013年该县1430名初中毕业生数学质量检测成绩为A级的人数为________人.
【解析】(1)20÷20%=100(名).
(2)×100%=30%.
(3)1430×20%=286(人).
答案:(1)100 (2)30% (3)286
三、解答题(每小题10分,共20分)
6.如图所示,报纸上一则广告绘制了如图的统计图,并称“乙品牌牛奶每天的销售量是甲品牌牛奶每天销售量的3倍”.请分析这则广告信息正确吗
【解析】这则广告的宣传是不正确的.从图中标明的数据看,甲品牌牛奶每天的销售量是510万袋,乙品牌牛奶每天的销售量是530万袋,只比甲品牌牛奶多了20万袋.乙品牌牛奶的销售量并不是甲品牌牛奶销售量的3倍.由于统计图制作的不规范,容易误导消费者认为乙品牌牛奶的销售量是甲品牌牛奶销售量的3倍.这则广告信息是不正确的.
【拓展延伸】作出决策的策略
实际问题要先选用有代表性的数据,然后通过整理数据,选用多种方式分析数据,作出正确、合理的决策.
7.(2014·大连高一检测)在一次人才招聘会上,有一家公司的招聘员说:“我们公司的收入水平很高,去年,在50名员工中,最高年收入达到了100万,他们年收入的平均数是3.5万.”
(1)你是否能够判断自己可以成为此公司的一名高收入者
(2)如果招聘员继续告诉你:“员工收入的变化范围是从0.5万到100万,”这个信息是否足以使你作出自己是否受聘的决定 为什么
(3)如果招聘员继续给你提供如下信息,员工收入的中间50%(即去掉最少的25%和最多的25%后所剩下的)的变化范围是1万到3万,你又该如何使用这条信息来作出是否受聘的决定
(4)为什么平均数比中间50%高很多 你能估计出收入的中位数是多少吗
【解析】(1)由于年收入的平均数是3.5万与最高年收入100万相差太大,所以不能判断一定能成为此公司的一名高收入者.
(2)由题可知员工收入的变化范围及平均数,高收入者只是极少数,所以不能作出是否受聘的决定.
(3)大部分员工的收入是1万到3万,这也是受聘该公司后最有可能的收入状况,所以这可以作出是否受聘的决定.
(4)收入极高的少数人对平均数影响较大,他们的收入与平均数相差太多.由于员工收入的中间50%的变化范围是1万到3万,可以估计收入的中位数大约是=2(万元).
