1.7 相关性 教案3
图片预览




文档简介
1.7
相关性
教案
教学目标:
知识与技能:
通过收集现实问题中两个变量的数据作出散点图,利用散点图直观认识变量间的相关关系。
过程与方法:
经历用不同的估算方法来描述两个变量线性相关的过程,能根据得到的近似直线进行简单的估计。
情感态度、价值观:
体会现实生活中大量存在着具有相关关系的两个量,感受统计与日常生活的密切联系。
教学重点:用不同的估算方法描述两个变量的线性相关关系
教学难点:用不同的估算方法描述两个变量的线性相关关系
教学活动
一、创设情境,认识相关关系
1.比较下面问题中两个变量之间的关系,说说它们的异同:
(1)真空中的自由落体运动,落体下落的距离h和下落的时间t有着h=gt2的关系;
(2)一辆行驶在公路上的汽车,每个时刻t都有一个确定的速度v,它们之间的关系。
(3)人的身高与体重之间的关系。
(4)人的年龄与血压之间的关系。
生独立思考后,展开全班交流。
学生可能回答这几个问题中两个变量之间都存在着关系,但前两个之间存在着函数关系,后两个之间的关系是不确定的。
变量间相关关系的概念:
自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系,叫做相关关系.
请同学们回忆一下,我们以前是否学过变量间的关系呢
两个变量间的函数关系.
相关关系与函数关系的异同点:
相同点:两者均是指两个变量间的关系.
不同点:①函数关系是一种确定的关系;相关关系是一种
非确定的关系.事实上,函数关系是两个非随机变量的关
系,而相关关系是随机变量与随机变量间的关系.
②函数关系是一种因果关系,而相关关系不一定是因果关
系,也可能是伴随关系.
2.如何刻画上述的这种关系呢?
(1)为了了解人的身高与体重的关系,我们随机地抽取9名15岁的男生,测得身高、体重如下表:
编号
1
2
3
4
5
6
7
8
9
身高/cm
165
157
155
175
168
157
178
160
163
体重/kg
52
44
45
55
54
47
62
50
53
如何刻画两组数据之间的关系呢?
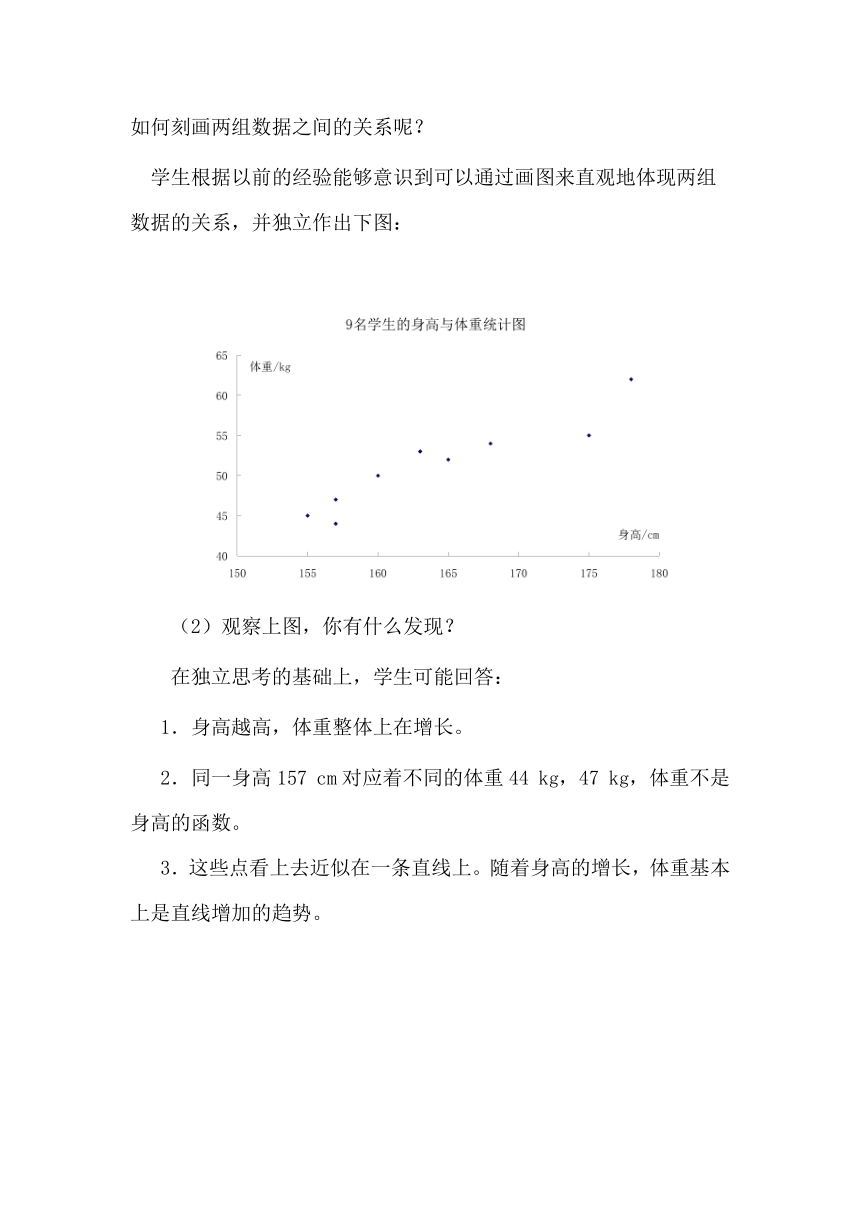
学生根据以前的经验能够意识到可以通过画图来直观地体现两组数据的关系,并独立作出下图:
(2)观察上图,你有什么发现?
在独立思考的基础上,学生可能回答:
1.身高越高,体重整体上在增长。
2.同一身高157
cm对应着不同的体重44
kg,47
kg,体重不是身高的函数。
3.这些点看上去近似在一条直线上。随着身高的增长,体重基本上是直线增加的趋势。
散点图:在考虑两个量的关系时,为了对变量之间的关系有一个大致的了解,人们通常将变量所对应的点描出来,这些点就组成了变量之间的一个图,通常称这种图叫做变量之间的散点图。
借助上面的散点图,教师介绍线性相关、非线性相关、不相关关系。
正相关:从刚才的散点图发现:身高越高,体重整体上在增长,点的位置散布在从左下角到右上角的区域。称它们成正相关。
负相关:但有的两个变量的相关,如下图所示:
如高原含氧量与海拔高度的相关关系,海平面以上,海拔高度越高,含氧量越少。作出散点图发现,它们散布在从左上角到右下角的区域内。又如汽车的载重和汽车每消耗1升汽油所行使的平均路程,称它们成负相关.
即学即用
1.下列关系中,是带有随机性相关关系的是
.
①正方形的边长与面积的关系;②水稻产量与施肥量之间的关系;③人的身高与年龄之间的关系;④降雪量与交通事故发生之间的关系.
答案:②③④
2.
下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的余弦值
B.
正方形边长和面积
C.正n边形的边数和它的内角和
D.
人的年龄和身高
答案;
D
典例分析:
一.利用散点图判断两个变量的相关性
例1: 某班5个学生的数学和物理成绩如表:
学生学科
A
B
C
D
E
数学
80
75
70
65
60
物理
70
66
68
64
62
画出散点图,并判断它们是否有相关关系?
解 以x轴表示数学成绩,y轴表示物理成绩,可得相应的散点图如下图所示:
由散点图可见,两者之间具有相关关系.
例2:有一位同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出热饮杯数与当天气温的对比表:
温度(℃)
-5
0
4
7
12
15
19
23
27
31
36
热饮杯数
156
150
132
128
130
116
104
89
93
76
54
(1)画出散点图;
(2)你能从散点图中发现气温与热饮销售杯数之间关系的一般规律吗?
解题导引 判断变量间是否线性相关,一种常用的简便可行的方法就是作散点图.
散点图是由大量数据点分布构成的,是定义在具有相关关系的两个变量基础之上的,对于性质不明确的两组数据可先作散点图,直观地分析它们有无关系及关系的密切程度.
解 (1)以x轴表示温度,以y轴表示热饮杯数,可作散点图,如图所示.
(2)从图中可以看出,各点散布在从左上角到右下角的区域里,因此,气温与热饮销售杯数之间是负相关关系,即气温越高,卖出去的热饮杯数越少.
从散点图可以看出,这些点大致分布在一条直线附近.
二、回归直线
如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线就叫做回归直线。
这条回归直线的方程,简称为回归方程。
1.如果所有的样本点都落在某一函数曲线上,变量之间具有函数关系
2.如果所有的样本点都落在某一函数曲线附近,变量之间就有相关关系
3.如果所有的样本点都落在某一直线附近,变量之间就有线性相关关系
只有散点图中的点呈条状集中在某一直线周围的时候,才可以说两个变量之间具有线性关系,才有两个变量的正线性相关和负线性相关的概念,才可以用回归直线来描述两个变量之间的关系
如何具体的求出这个回归方程呢?
方案一:采用测量的方法:先画一条直线,测量出各点到它的距离,然后移动直线,到达一个使距离之和最小的位置,测量出此时直线的斜率和截距,就得到回归方程。
整体上最接近
方案二:
在图中选取两点画直线,使得直线两侧的点的个数基本相同。
方案三:
在散点图中多取几组点,确定几条直线的方程,分别求出各条直线的斜率和截距的平均数,将这两个平均数作为回归方程的斜率和截距。
上述三种方案均有一定的道理,但可靠性不强,我们回到回归直线的定义。
如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线就叫做回归直线。
求回归方程的关键是如何用数学的方法来刻画“从整体上看,各点与直线的偏差最小”。
自测自评
1
.
下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的余弦值
B.正方形边长和面积
C.正n边形的边数和它的内角和
D.人的年龄和身高
1.答案:
D
2.对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);对变量u,v有观测数据(ui,vi)(i=1,2,…,10),得散点图(2).由这两个散点图可以判断( )
A.变量x与y正相关,u与v正相关
B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关
D.变量x与y负相关,u与v负相关
2.
答案:
C
3.下列两个变量之间的关系不具有线性关系的是
(
)
A.小麦产量与施肥值
B.球的体积与表面积
C.蛋鸭产蛋个数与饲养天数
D.甘蔗的含糖量与生长期的日照天数
答案:B
4.下列变量之间是函数关系的是
(
)
A.
当速度一定时,路程和时间
B.光照时间和果树亩产量
C.降雪量和交通事故发生率
D.每亩施用肥料量和粮食亩产量
答案:A
5.下面现象间的关系属于线性相关关系的是
(
)
A.圆的周长和它的半径之间的关系
B.价格不变条件下,商品销售额与销售量之间的关系
C.家庭收入愈多,其消费支出也有增长的趋势
D.正方形面积和它的边长之间的关系
答案:C
6.下列关系中是函数关系的是
(
)
A.球的半径长度和体积的关系
B.农作物收获和施肥量的关系
C.商品销售额和利润的关系
D.产品产量与单位成品成本的关系
答案:A
课堂小结
1.变量间相关关系的概念
2.散点图
正相关
负相关
3.回归直线
相关性
教案
教学目标:
知识与技能:
通过收集现实问题中两个变量的数据作出散点图,利用散点图直观认识变量间的相关关系。
过程与方法:
经历用不同的估算方法来描述两个变量线性相关的过程,能根据得到的近似直线进行简单的估计。
情感态度、价值观:
体会现实生活中大量存在着具有相关关系的两个量,感受统计与日常生活的密切联系。
教学重点:用不同的估算方法描述两个变量的线性相关关系
教学难点:用不同的估算方法描述两个变量的线性相关关系
教学活动
一、创设情境,认识相关关系
1.比较下面问题中两个变量之间的关系,说说它们的异同:
(1)真空中的自由落体运动,落体下落的距离h和下落的时间t有着h=gt2的关系;
(2)一辆行驶在公路上的汽车,每个时刻t都有一个确定的速度v,它们之间的关系。
(3)人的身高与体重之间的关系。
(4)人的年龄与血压之间的关系。
生独立思考后,展开全班交流。
学生可能回答这几个问题中两个变量之间都存在着关系,但前两个之间存在着函数关系,后两个之间的关系是不确定的。
变量间相关关系的概念:
自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系,叫做相关关系.
请同学们回忆一下,我们以前是否学过变量间的关系呢
两个变量间的函数关系.
相关关系与函数关系的异同点:
相同点:两者均是指两个变量间的关系.
不同点:①函数关系是一种确定的关系;相关关系是一种
非确定的关系.事实上,函数关系是两个非随机变量的关
系,而相关关系是随机变量与随机变量间的关系.
②函数关系是一种因果关系,而相关关系不一定是因果关
系,也可能是伴随关系.
2.如何刻画上述的这种关系呢?
(1)为了了解人的身高与体重的关系,我们随机地抽取9名15岁的男生,测得身高、体重如下表:
编号
1
2
3
4
5
6
7
8
9
身高/cm
165
157
155
175
168
157
178
160
163
体重/kg
52
44
45
55
54
47
62
50
53
如何刻画两组数据之间的关系呢?
学生根据以前的经验能够意识到可以通过画图来直观地体现两组数据的关系,并独立作出下图:
(2)观察上图,你有什么发现?
在独立思考的基础上,学生可能回答:
1.身高越高,体重整体上在增长。
2.同一身高157
cm对应着不同的体重44
kg,47
kg,体重不是身高的函数。
3.这些点看上去近似在一条直线上。随着身高的增长,体重基本上是直线增加的趋势。
散点图:在考虑两个量的关系时,为了对变量之间的关系有一个大致的了解,人们通常将变量所对应的点描出来,这些点就组成了变量之间的一个图,通常称这种图叫做变量之间的散点图。
借助上面的散点图,教师介绍线性相关、非线性相关、不相关关系。
正相关:从刚才的散点图发现:身高越高,体重整体上在增长,点的位置散布在从左下角到右上角的区域。称它们成正相关。
负相关:但有的两个变量的相关,如下图所示:
如高原含氧量与海拔高度的相关关系,海平面以上,海拔高度越高,含氧量越少。作出散点图发现,它们散布在从左上角到右下角的区域内。又如汽车的载重和汽车每消耗1升汽油所行使的平均路程,称它们成负相关.
即学即用
1.下列关系中,是带有随机性相关关系的是
.
①正方形的边长与面积的关系;②水稻产量与施肥量之间的关系;③人的身高与年龄之间的关系;④降雪量与交通事故发生之间的关系.
答案:②③④
2.
下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的余弦值
B.
正方形边长和面积
C.正n边形的边数和它的内角和
D.
人的年龄和身高
答案;
D
典例分析:
一.利用散点图判断两个变量的相关性
例1: 某班5个学生的数学和物理成绩如表:
学生学科
A
B
C
D
E
数学
80
75
70
65
60
物理
70
66
68
64
62
画出散点图,并判断它们是否有相关关系?
解 以x轴表示数学成绩,y轴表示物理成绩,可得相应的散点图如下图所示:
由散点图可见,两者之间具有相关关系.
例2:有一位同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出热饮杯数与当天气温的对比表:
温度(℃)
-5
0
4
7
12
15
19
23
27
31
36
热饮杯数
156
150
132
128
130
116
104
89
93
76
54
(1)画出散点图;
(2)你能从散点图中发现气温与热饮销售杯数之间关系的一般规律吗?
解题导引 判断变量间是否线性相关,一种常用的简便可行的方法就是作散点图.
散点图是由大量数据点分布构成的,是定义在具有相关关系的两个变量基础之上的,对于性质不明确的两组数据可先作散点图,直观地分析它们有无关系及关系的密切程度.
解 (1)以x轴表示温度,以y轴表示热饮杯数,可作散点图,如图所示.
(2)从图中可以看出,各点散布在从左上角到右下角的区域里,因此,气温与热饮销售杯数之间是负相关关系,即气温越高,卖出去的热饮杯数越少.
从散点图可以看出,这些点大致分布在一条直线附近.
二、回归直线
如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线就叫做回归直线。
这条回归直线的方程,简称为回归方程。
1.如果所有的样本点都落在某一函数曲线上,变量之间具有函数关系
2.如果所有的样本点都落在某一函数曲线附近,变量之间就有相关关系
3.如果所有的样本点都落在某一直线附近,变量之间就有线性相关关系
只有散点图中的点呈条状集中在某一直线周围的时候,才可以说两个变量之间具有线性关系,才有两个变量的正线性相关和负线性相关的概念,才可以用回归直线来描述两个变量之间的关系
如何具体的求出这个回归方程呢?
方案一:采用测量的方法:先画一条直线,测量出各点到它的距离,然后移动直线,到达一个使距离之和最小的位置,测量出此时直线的斜率和截距,就得到回归方程。
整体上最接近
方案二:
在图中选取两点画直线,使得直线两侧的点的个数基本相同。
方案三:
在散点图中多取几组点,确定几条直线的方程,分别求出各条直线的斜率和截距的平均数,将这两个平均数作为回归方程的斜率和截距。
上述三种方案均有一定的道理,但可靠性不强,我们回到回归直线的定义。
如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线就叫做回归直线。
求回归方程的关键是如何用数学的方法来刻画“从整体上看,各点与直线的偏差最小”。
自测自评
1
.
下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的余弦值
B.正方形边长和面积
C.正n边形的边数和它的内角和
D.人的年龄和身高
1.答案:
D
2.对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);对变量u,v有观测数据(ui,vi)(i=1,2,…,10),得散点图(2).由这两个散点图可以判断( )
A.变量x与y正相关,u与v正相关
B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关
D.变量x与y负相关,u与v负相关
2.
答案:
C
3.下列两个变量之间的关系不具有线性关系的是
(
)
A.小麦产量与施肥值
B.球的体积与表面积
C.蛋鸭产蛋个数与饲养天数
D.甘蔗的含糖量与生长期的日照天数
答案:B
4.下列变量之间是函数关系的是
(
)
A.
当速度一定时,路程和时间
B.光照时间和果树亩产量
C.降雪量和交通事故发生率
D.每亩施用肥料量和粮食亩产量
答案:A
5.下面现象间的关系属于线性相关关系的是
(
)
A.圆的周长和它的半径之间的关系
B.价格不变条件下,商品销售额与销售量之间的关系
C.家庭收入愈多,其消费支出也有增长的趋势
D.正方形面积和它的边长之间的关系
答案:C
6.下列关系中是函数关系的是
(
)
A.球的半径长度和体积的关系
B.农作物收获和施肥量的关系
C.商品销售额和利润的关系
D.产品产量与单位成品成本的关系
答案:A
课堂小结
1.变量间相关关系的概念
2.散点图
正相关
负相关
3.回归直线
