1.7 相关性 同步测试(含答案)
图片预览



文档简介
1.7
相 关 性
同步测试
一、选择题(每小题4分,共16分)
1.(2014·潍坊高一检测)汽车尾气是影响空气质量的重要因素之一,那么汽车尾气与空气质量之间存在的关系是 ( )
A.相关
B.不相关
C.函数关系
D.不确定
【解析】选A.因为汽车尾气影响空气质量,并且汽车尾气越多,空气质量就越不好,但汽车尾气与空气质量之间存在的关系不是确定的,是相关关系.
2.某研究小组在一项实验中获得一组关于y,t之间的数据,将其整理后得到如图的散点图,下列函数中,最能近似刻画y与t之间关系的是 ( )
A.y=2t
B.y=2t2
C.y=t3
D.y=log2t
【解析】选D.结合对数函数图像的特点以及散点图中样本点的分布规律可判断.
3.下列四个图各反映了两个变量的某种关系,其中可以看作具有较强线性相关关系的是 ( )
A.①③
B.①④
C.②③
D.①②
【解析】选B.因为两个变量的散点图,
若样本点成带状分布,且分布在一条直线附近,则两个变量具有线性相关关系,
所以两个变量具有线性相关关系的图是①和④.
【误区警示】解答此题时常常因对线性相关关系的概念理解有误导致错误判断,线性关系中的“线”是直线,不包括曲线.
4.(2014·合肥高一检测)下列说法正确的是 ( )
A.相关关系是函数关系
B.函数关系是相关关系
C.线性相关关系是一次函数关系
D.相关关系有两种,分别是线性相关关系和非线性相关关系
【解析】选D.函数关系和相关关系互不包含,所以A,B,C三项不正确;根据定义,相关关系有两种,分别是线性相关关系和非线性相关关系,故选D项.
二、填空题(每小题5分,共10分)
5.据两个变量x,y之间的观测数据画成散点图如图,这两个变量是否具有线性相关关系________(填“是”或“否”).
【解析】散点图中的点不存在一定的规律性,故这两个变量不具有线性相关关系.
答案:否
6.2013年秋季,我国部分地区发生甲型流感,党和政府采取果断措施,使疫情得到控制.下表是某体检站记录的9月1日~9月12日体检中发烧人数,并给出散点图如图
日期
9.1
9.2
9.3
9.4
9.5
9.6
人数
100
109
115
118
121
131
日期
9.7
9.8
9.9
9.10
9.11
9.12
人数
141
152
158
175
186
203
下列说法:
①根据此散点图,可以判断日期与发烧人数具有线性相关关系;
②根据此散点图,可以判断日期与发烧人数具有一次函数关系.
其中正确的是__________.
【解析】由散点图可以发现样本点大致分布在一条直线附近,所以可以判断日期与发烧人数具有线性相关关系.
答案:①
三、解答题(每小题12分,共24分)
7.5名学生的数学成绩和化学成绩如表所示:
试画出散点图,并判断它们是否具有线性相关关系.
【解析】以x轴表示数学成绩,y轴表示化学成绩,可得相应的散点图如图所示.由散点图可知,两者之间具有线性相关关系.
8.(2014·大连高一检测)某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
x
2
4
5
6
8
y
30
40
60
50
70
(1)根据上表中的数据制成散点图,你能从散点图中发现广告费支出与销售额之间的近似关系吗
(2)如果近似成线性关系,请画出一条直线来表示这种线性关系.
(3)如果广告费支出为7百万元,请估计此时的销售额为多少.
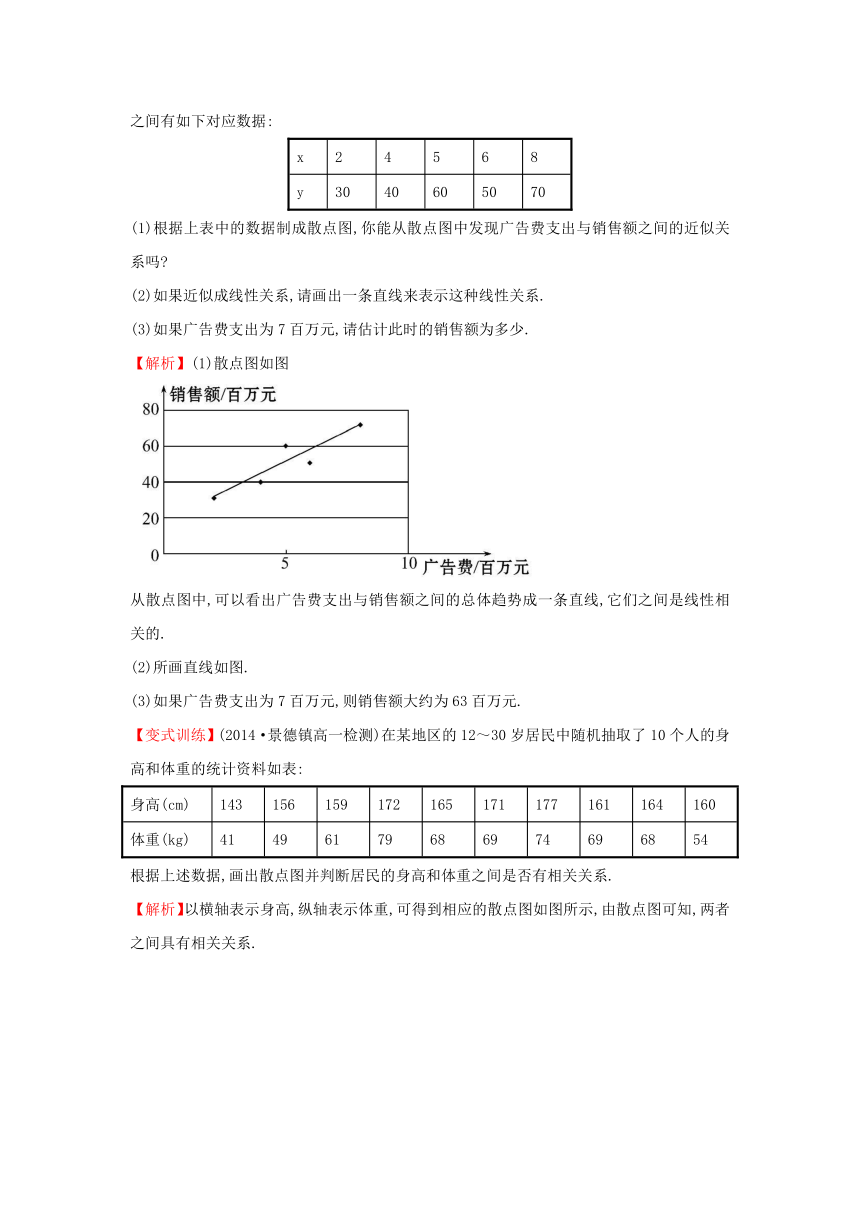
【解析】(1)散点图如图
从散点图中,可以看出广告费支出与销售额之间的总体趋势成一条直线,它们之间是线性相关的.
(2)所画直线如图.
(3)如果广告费支出为7百万元,则销售额大约为63百万元.
【变式训练】(2014·景德镇高一检测)在某地区的12~30岁居民中随机抽取了10个人的身高和体重的统计资料如表:
身高(cm)
143
156
159
172
165
171
177
161
164
160
体重(kg)
41
49
61
79
68
69
74
69
68
54
根据上述数据,画出散点图并判断居民的身高和体重之间是否有相关关系.
【解析】以横轴表示身高,纵轴表示体重,可得到相应的散点图如图所示,由散点图可知,两者之间具有相关关系.
一、选择题(每小题4分,共12分)
1.如图所示,有5组(x,y)数据对应的点,去掉哪个点之后,剩下的4个点对应的数据可以表明两变量成线性相关关系 ( )
A.E
B.D
C.B
D.A
【解析】选B.点A,B,C,E集中在一条直线附近,而点D远离此直线,故应去掉D点.
2.今有一组数据如下:
t
1.99
3.0
4.0
5.1
6.12
v
1.5
4.04
7.5
12
18.01
在以下四个模拟函数中,最适合这组数据的函数是 ( )
A.v=log2t
B.v=lot
C.v=
D.v=2t-2
【解析】选C.把t看作自变量,v看作其函数值,从表中数据的变化趋势看,函数递增的速度不断增加.对照四个选项,A选项是对数型函数,其递增速度不断变慢.B选项随着t的增大v变小,故不能选.D选项以一个恒定的幅度变化,其图像是直线,不符合本题的变化规律.C选项是二次型,对比知,其最接近实验数据的变化趋势.
3.(2014·深圳高一检测)对于给定的两个变量的统计数据,下列说法正确的是
( )
A.都可以分析出两个变量的关系
B.都可以用一条直线近似表示两者的关系
C.都可以作出散点图
D.都可以用确定的表达式表示两者的关系
【解题指南】给出一组样本数据,总可以根据相应的几对有序数对,作出对应的散点图,但不一定能分析出两个变量的关系,不一定存在直线来模拟这组数据.
【解析】选C.给出一组样本数据,总可以作出相应的散点图,故C正确,但不一定能分析出两个变量的关系,故A不正确,更不一定符合线性相关,不一定用一条直线近似表示,故B不正确,两个变量的统计数据不一定有函数关系,故D不正确.
二、填空题(每小题4分,共8分)
4.(2014·济南高一检测)下面变量间的关系属于线性相关关系的是__________.
①圆的周长和它的半径之间的关系;
②价格不变条件下,商品销售额与销售量之间的关系;
③家庭收入与其消费支出的关系;
④人的体重与饭量的关系.
【解析】①②是函数关系,③④是相关关系,且为线性相关关系.
答案:③④
5.某市居民2010~2014年家庭年平均收入x(单位:万元)与年平均支出y(单位:万元)的统计资料如表所示:
年份
2010
2011
2012
2013
2014
收入(x)
11.5
12.1
13
13.3
15
支出(y)
6.8
8.8
9.8
10
12
根据统计资料,居民家庭年平均收入的中位数是______,家庭年平均收入与年平均支出有________相关关系.
【解题指南】求中位数要先排序,再根据数据个数确定中位数的计算方法,奇数个取“中间”,偶数个取中间两数的平均数.
【解析】把2010~2014年家庭年平均收入按从小到大的顺序排列为11.5,12.1,13,13.3,15,因此中位数为13万元,由统计资料可以看出,当年平均收入增多时,年平均支出也增多,画散点图可知两者之间具有线性相关关系.
答案:13万元 线性
三、解答题(每小题10分,共20分)
6.李老师为了了解学生的计算能力,对某同学进行了10次测验,收集数据如下:
题数x/道
5
10
15
20
25
30
35
40
45
50
做题时间y/分钟
9
19
26
37
48
52
61
73
81
89
画出散点图,并判断它们是否有线性相关关系.
【解析】散点图如图:
由散点图可以看出,两者之间具有线性相关关系.
【拓展延伸】散点图的作用
(1)散点图具有直观、形象的特点,可以直接观察出样本点的分布规律.
(2)由散点图中样本点的分布特点和规律可以确定变量之间是否具有相关关系,是否具有线性相关关系,进而确定与其关系拟合的曲线类型.
7.(2014·西安高一检测)调查某班学习数学所用时间x(时/周)与某次测验成绩y(分)得到如下数据:
x
16
18
17
20
19
15
y
93
95
87
95
87
80
(1)作出散点图,分析变量x与y之间的关系.
(2)是否当x增大时,y会一直增大
【解析】(1)画出散点图如图所示.
由散点图可知,变量x与y之间具有线性相关关系.
(2)在某一范围内,随着x的增加,y会出现增加的趋势,但当超过一定范围时,随着x的增大,y不会一直增大.
相 关 性
同步测试
一、选择题(每小题4分,共16分)
1.(2014·潍坊高一检测)汽车尾气是影响空气质量的重要因素之一,那么汽车尾气与空气质量之间存在的关系是 ( )
A.相关
B.不相关
C.函数关系
D.不确定
【解析】选A.因为汽车尾气影响空气质量,并且汽车尾气越多,空气质量就越不好,但汽车尾气与空气质量之间存在的关系不是确定的,是相关关系.
2.某研究小组在一项实验中获得一组关于y,t之间的数据,将其整理后得到如图的散点图,下列函数中,最能近似刻画y与t之间关系的是 ( )
A.y=2t
B.y=2t2
C.y=t3
D.y=log2t
【解析】选D.结合对数函数图像的特点以及散点图中样本点的分布规律可判断.
3.下列四个图各反映了两个变量的某种关系,其中可以看作具有较强线性相关关系的是 ( )
A.①③
B.①④
C.②③
D.①②
【解析】选B.因为两个变量的散点图,
若样本点成带状分布,且分布在一条直线附近,则两个变量具有线性相关关系,
所以两个变量具有线性相关关系的图是①和④.
【误区警示】解答此题时常常因对线性相关关系的概念理解有误导致错误判断,线性关系中的“线”是直线,不包括曲线.
4.(2014·合肥高一检测)下列说法正确的是 ( )
A.相关关系是函数关系
B.函数关系是相关关系
C.线性相关关系是一次函数关系
D.相关关系有两种,分别是线性相关关系和非线性相关关系
【解析】选D.函数关系和相关关系互不包含,所以A,B,C三项不正确;根据定义,相关关系有两种,分别是线性相关关系和非线性相关关系,故选D项.
二、填空题(每小题5分,共10分)
5.据两个变量x,y之间的观测数据画成散点图如图,这两个变量是否具有线性相关关系________(填“是”或“否”).
【解析】散点图中的点不存在一定的规律性,故这两个变量不具有线性相关关系.
答案:否
6.2013年秋季,我国部分地区发生甲型流感,党和政府采取果断措施,使疫情得到控制.下表是某体检站记录的9月1日~9月12日体检中发烧人数,并给出散点图如图
日期
9.1
9.2
9.3
9.4
9.5
9.6
人数
100
109
115
118
121
131
日期
9.7
9.8
9.9
9.10
9.11
9.12
人数
141
152
158
175
186
203
下列说法:
①根据此散点图,可以判断日期与发烧人数具有线性相关关系;
②根据此散点图,可以判断日期与发烧人数具有一次函数关系.
其中正确的是__________.
【解析】由散点图可以发现样本点大致分布在一条直线附近,所以可以判断日期与发烧人数具有线性相关关系.
答案:①
三、解答题(每小题12分,共24分)
7.5名学生的数学成绩和化学成绩如表所示:
试画出散点图,并判断它们是否具有线性相关关系.
【解析】以x轴表示数学成绩,y轴表示化学成绩,可得相应的散点图如图所示.由散点图可知,两者之间具有线性相关关系.
8.(2014·大连高一检测)某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
x
2
4
5
6
8
y
30
40
60
50
70
(1)根据上表中的数据制成散点图,你能从散点图中发现广告费支出与销售额之间的近似关系吗
(2)如果近似成线性关系,请画出一条直线来表示这种线性关系.
(3)如果广告费支出为7百万元,请估计此时的销售额为多少.
【解析】(1)散点图如图
从散点图中,可以看出广告费支出与销售额之间的总体趋势成一条直线,它们之间是线性相关的.
(2)所画直线如图.
(3)如果广告费支出为7百万元,则销售额大约为63百万元.
【变式训练】(2014·景德镇高一检测)在某地区的12~30岁居民中随机抽取了10个人的身高和体重的统计资料如表:
身高(cm)
143
156
159
172
165
171
177
161
164
160
体重(kg)
41
49
61
79
68
69
74
69
68
54
根据上述数据,画出散点图并判断居民的身高和体重之间是否有相关关系.
【解析】以横轴表示身高,纵轴表示体重,可得到相应的散点图如图所示,由散点图可知,两者之间具有相关关系.
一、选择题(每小题4分,共12分)
1.如图所示,有5组(x,y)数据对应的点,去掉哪个点之后,剩下的4个点对应的数据可以表明两变量成线性相关关系 ( )
A.E
B.D
C.B
D.A
【解析】选B.点A,B,C,E集中在一条直线附近,而点D远离此直线,故应去掉D点.
2.今有一组数据如下:
t
1.99
3.0
4.0
5.1
6.12
v
1.5
4.04
7.5
12
18.01
在以下四个模拟函数中,最适合这组数据的函数是 ( )
A.v=log2t
B.v=lot
C.v=
D.v=2t-2
【解析】选C.把t看作自变量,v看作其函数值,从表中数据的变化趋势看,函数递增的速度不断增加.对照四个选项,A选项是对数型函数,其递增速度不断变慢.B选项随着t的增大v变小,故不能选.D选项以一个恒定的幅度变化,其图像是直线,不符合本题的变化规律.C选项是二次型,对比知,其最接近实验数据的变化趋势.
3.(2014·深圳高一检测)对于给定的两个变量的统计数据,下列说法正确的是
( )
A.都可以分析出两个变量的关系
B.都可以用一条直线近似表示两者的关系
C.都可以作出散点图
D.都可以用确定的表达式表示两者的关系
【解题指南】给出一组样本数据,总可以根据相应的几对有序数对,作出对应的散点图,但不一定能分析出两个变量的关系,不一定存在直线来模拟这组数据.
【解析】选C.给出一组样本数据,总可以作出相应的散点图,故C正确,但不一定能分析出两个变量的关系,故A不正确,更不一定符合线性相关,不一定用一条直线近似表示,故B不正确,两个变量的统计数据不一定有函数关系,故D不正确.
二、填空题(每小题4分,共8分)
4.(2014·济南高一检测)下面变量间的关系属于线性相关关系的是__________.
①圆的周长和它的半径之间的关系;
②价格不变条件下,商品销售额与销售量之间的关系;
③家庭收入与其消费支出的关系;
④人的体重与饭量的关系.
【解析】①②是函数关系,③④是相关关系,且为线性相关关系.
答案:③④
5.某市居民2010~2014年家庭年平均收入x(单位:万元)与年平均支出y(单位:万元)的统计资料如表所示:
年份
2010
2011
2012
2013
2014
收入(x)
11.5
12.1
13
13.3
15
支出(y)
6.8
8.8
9.8
10
12
根据统计资料,居民家庭年平均收入的中位数是______,家庭年平均收入与年平均支出有________相关关系.
【解题指南】求中位数要先排序,再根据数据个数确定中位数的计算方法,奇数个取“中间”,偶数个取中间两数的平均数.
【解析】把2010~2014年家庭年平均收入按从小到大的顺序排列为11.5,12.1,13,13.3,15,因此中位数为13万元,由统计资料可以看出,当年平均收入增多时,年平均支出也增多,画散点图可知两者之间具有线性相关关系.
答案:13万元 线性
三、解答题(每小题10分,共20分)
6.李老师为了了解学生的计算能力,对某同学进行了10次测验,收集数据如下:
题数x/道
5
10
15
20
25
30
35
40
45
50
做题时间y/分钟
9
19
26
37
48
52
61
73
81
89
画出散点图,并判断它们是否有线性相关关系.
【解析】散点图如图:
由散点图可以看出,两者之间具有线性相关关系.
【拓展延伸】散点图的作用
(1)散点图具有直观、形象的特点,可以直接观察出样本点的分布规律.
(2)由散点图中样本点的分布特点和规律可以确定变量之间是否具有相关关系,是否具有线性相关关系,进而确定与其关系拟合的曲线类型.
7.(2014·西安高一检测)调查某班学习数学所用时间x(时/周)与某次测验成绩y(分)得到如下数据:
x
16
18
17
20
19
15
y
93
95
87
95
87
80
(1)作出散点图,分析变量x与y之间的关系.
(2)是否当x增大时,y会一直增大
【解析】(1)画出散点图如图所示.
由散点图可知,变量x与y之间具有线性相关关系.
(2)在某一范围内,随着x的增加,y会出现增加的趋势,但当超过一定范围时,随着x的增大,y不会一直增大.
