浙江嵊泗中学09-10学年第一学期期末试卷高二数学(文)
文档属性
| 名称 | 浙江嵊泗中学09-10学年第一学期期末试卷高二数学(文) |

|
|
| 格式 | rar | ||
| 文件大小 | 242.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-12 00:00:00 | ||
图片预览


文档简介
嵊泗中学09-10学年第一学期期末试卷
高二数(文)
一、选择题:(本大题共10小题,每小题5分,共50分)
1、复数的共轭复数是( )
A. B. C. D.
2、一个年级有12个班,每个班有50名同学,随机编号为1~50,为了了解他们在课外的兴趣,要求每班第40号同学留下来进行问卷调查,这里运用的抽样方法是( )
A、抽签法 B、分层抽样法
C、系统抽样法 D、随机数表法
3、全称命题:的否定是( )
A. B.
C. D.
4、下列表述正确的是( )
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理。
A.①②③ B.②③④ C.②④⑤ D.①③⑤
5、200辆汽车通过某一段公路时的时速的频率分布直方图
如右图所示,则时速在[60,70)的汽车大约有( )
A. 30辆 B. 40辆
C. 60辆 D. 80辆
6、条件甲:“”,条件乙:“方程表示双曲线”,那么甲是乙的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
7、从装有个红球和个?虻拇?谌稳∏颍?敲椿コ獠欢粤⒌牧礁鍪录?牵? )
A.至少有一个?蛴攵际屈球 B.至多有一个?蛴攵际屈球
C.至少有一个?蛴胫辽儆幸桓龊烨? D.恰有一个?蛴肭∮辛礁鳇球
8、下面说法:
①如果一组数据的众数是5,那么这组数据中出现次数最多的数是5;
②如果一组数据的平均数是0,那么这组数据的中位数为0;
③如果一组数据1,2,,4的中位数是3,那么;
④如果一组数据的平均数是正数,那么这组数据都是正数。
其中错误的个数是( )
A.1 B.2 C.3 D.4
9、已知椭圆的左焦点为,右顶点为,点在椭圆上,且轴, 直线交轴于点.若,则椭圆的离心率是(
A. B. C. D.
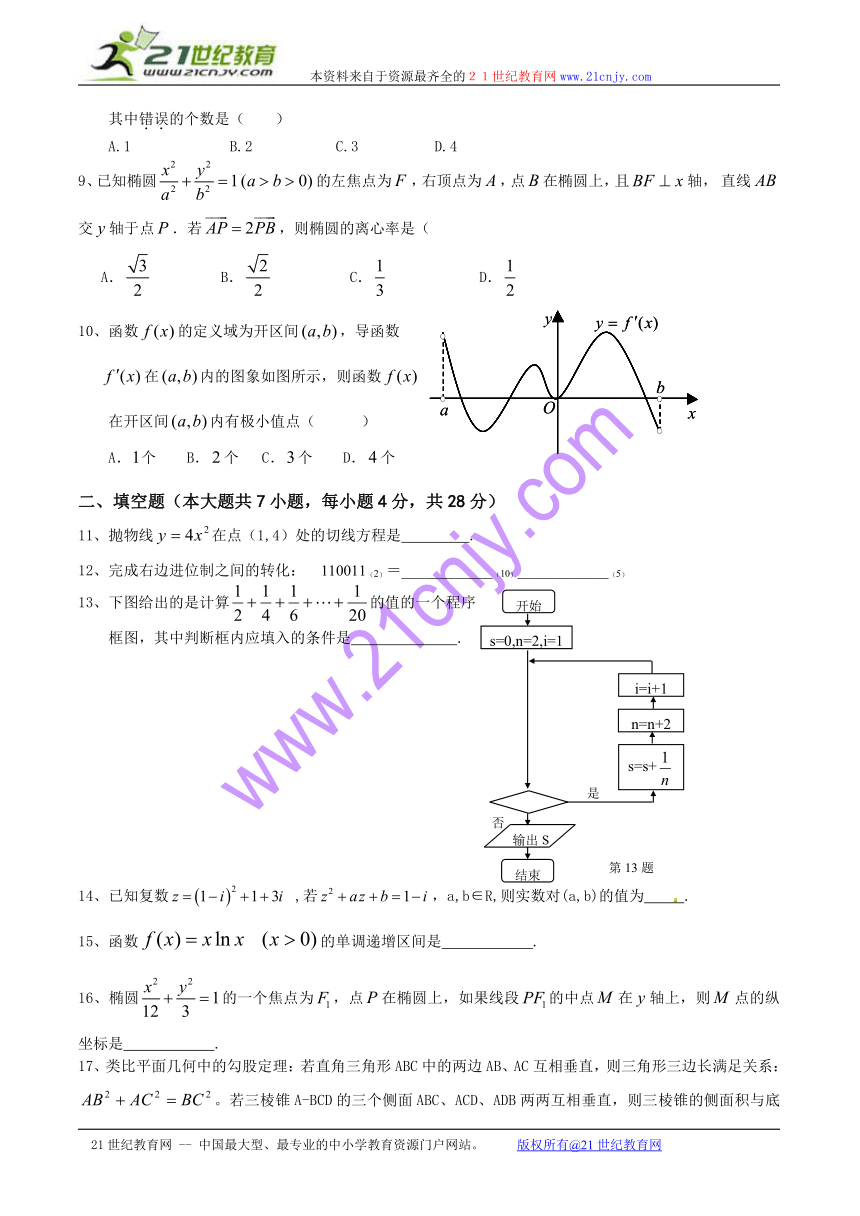
10、函数的定义域为开区间,导函数
在内的图象如图所示,则函数
在开区间内有极小值点( )
A.个 B.个 C.个 D.个
二、填空题(本大题共7小题,每小题4分,共28分)
11、抛物线在点(1,4)处的切线方程是 .
12、完成右边进位制之间的转化: 110011(2)=____________(10)____________(5)
13、下图给出的是计算的值的一个程序
框图,其中判断框内应填入的条件是 .
14、已知复数 ,若,a,b∈R,则实数对(a,b)的值为 .
15、函数的单调递增区间是 .
16、椭圆的一个焦点为,点在椭圆上,如果线段的中点在轴上,则点的纵坐标是 .
17、类比平面几何中的勾股定理:若直角三角形ABC中的两边AB、AC互相垂直,则三角形三边长满足关系:。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积满足的关系为 .
三、解答题:(本大题共7小题,共72分)
18、(本小题满分14分)
某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别是0.3、0.2、0.1、0.4,求:
(1)他乘火车或乘飞机去的概率;
(2)他不乘轮船去的概率
(3)如果他去的概率为0.5,请问他有可能是乘何种交通工具去的?
19、(本小题满分14分)
用长为18m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?w.w
20、(本小题满分14分)
已知,试证明至少有一个不小于1.
21、(本小题满分15分)
如图,已知抛物线方程为
⑴直线过抛物线的焦点F,且垂直于x轴,与抛物线交于
A、B两点,求AB的长度;
⑵直线过抛物线的焦点,且倾斜角为,直线与抛
物线相交于C、D两点,O为原点。求△OCD的面积。
22、(本小题满分15分)已知是函数的一个极值点,其中,
(I)求与的关系式;
(II)求的单调区间;
(III)当时,函数的图象上任意一点的切线斜率恒大于3,求的取值范围.
嵊泗中学09-10学年第一学期期末试卷
高二数(文)答案
一、选择题:(本大题共10小题,每小题5分,共50分)
1
2
3
4
5
6
7
8
9
10
B
C
D
D
D
A
D
B
D
A
二、填空题(本大题共7小题,每小题4分,共28分)
11、y=8x-4 12、51 201 13、 14、(-3,4) 15、(1/e,+∞) 16、
17、
三、解答题:(本大题共7小题,共72分)
18、解:设乘火车去开会为事件A,乘轮船去开会为事件B,乘汽车去为事件C,乘飞机去为事件D,它们彼此互斥。……………………………2分
(1)P(A+D)=P(A)+P(D)=0.3+0.4=0.7……………………………6分
(2)P=1-P(B)=1-0.2=0.8……………………………10分
(3)P=0.5=0.2+0.3=0.1+0.4
21、(15分)解:⑴∵抛物线方程为,∴焦点,又直线过焦点,且垂直于x轴,∴的方程为,联立方程组,解得 ∴,。……………………………(6分)
⑵由⑴焦点,直线倾斜角为,直线的斜率,其方程为
,设,联立方程组
。∴,又,∴△OCD的面积为。……………(15分)
22、(Ⅰ)解:.
因为是的一个极值点,所以,即.
所以………………… 3分
设,其函数图象的开口向上.
由题意(*)式恒成立,
又.
即的取值范围是………………… 15分
解法二:由已知,得,即,
高二数(文)
一、选择题:(本大题共10小题,每小题5分,共50分)
1、复数的共轭复数是( )
A. B. C. D.
2、一个年级有12个班,每个班有50名同学,随机编号为1~50,为了了解他们在课外的兴趣,要求每班第40号同学留下来进行问卷调查,这里运用的抽样方法是( )
A、抽签法 B、分层抽样法
C、系统抽样法 D、随机数表法
3、全称命题:的否定是( )
A. B.
C. D.
4、下列表述正确的是( )
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理。
A.①②③ B.②③④ C.②④⑤ D.①③⑤
5、200辆汽车通过某一段公路时的时速的频率分布直方图
如右图所示,则时速在[60,70)的汽车大约有( )
A. 30辆 B. 40辆
C. 60辆 D. 80辆
6、条件甲:“”,条件乙:“方程表示双曲线”,那么甲是乙的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
7、从装有个红球和个?虻拇?谌稳∏颍?敲椿コ獠欢粤⒌牧礁鍪录?牵? )
A.至少有一个?蛴攵际屈球 B.至多有一个?蛴攵际屈球
C.至少有一个?蛴胫辽儆幸桓龊烨? D.恰有一个?蛴肭∮辛礁鳇球
8、下面说法:
①如果一组数据的众数是5,那么这组数据中出现次数最多的数是5;
②如果一组数据的平均数是0,那么这组数据的中位数为0;
③如果一组数据1,2,,4的中位数是3,那么;
④如果一组数据的平均数是正数,那么这组数据都是正数。
其中错误的个数是( )
A.1 B.2 C.3 D.4
9、已知椭圆的左焦点为,右顶点为,点在椭圆上,且轴, 直线交轴于点.若,则椭圆的离心率是(
A. B. C. D.
10、函数的定义域为开区间,导函数
在内的图象如图所示,则函数
在开区间内有极小值点( )
A.个 B.个 C.个 D.个
二、填空题(本大题共7小题,每小题4分,共28分)
11、抛物线在点(1,4)处的切线方程是 .
12、完成右边进位制之间的转化: 110011(2)=____________(10)____________(5)
13、下图给出的是计算的值的一个程序
框图,其中判断框内应填入的条件是 .
14、已知复数 ,若,a,b∈R,则实数对(a,b)的值为 .
15、函数的单调递增区间是 .
16、椭圆的一个焦点为,点在椭圆上,如果线段的中点在轴上,则点的纵坐标是 .
17、类比平面几何中的勾股定理:若直角三角形ABC中的两边AB、AC互相垂直,则三角形三边长满足关系:。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积满足的关系为 .
三、解答题:(本大题共7小题,共72分)
18、(本小题满分14分)
某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别是0.3、0.2、0.1、0.4,求:
(1)他乘火车或乘飞机去的概率;
(2)他不乘轮船去的概率
(3)如果他去的概率为0.5,请问他有可能是乘何种交通工具去的?
19、(本小题满分14分)
用长为18m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?w.w
20、(本小题满分14分)
已知,试证明至少有一个不小于1.
21、(本小题满分15分)
如图,已知抛物线方程为
⑴直线过抛物线的焦点F,且垂直于x轴,与抛物线交于
A、B两点,求AB的长度;
⑵直线过抛物线的焦点,且倾斜角为,直线与抛
物线相交于C、D两点,O为原点。求△OCD的面积。
22、(本小题满分15分)已知是函数的一个极值点,其中,
(I)求与的关系式;
(II)求的单调区间;
(III)当时,函数的图象上任意一点的切线斜率恒大于3,求的取值范围.
嵊泗中学09-10学年第一学期期末试卷
高二数(文)答案
一、选择题:(本大题共10小题,每小题5分,共50分)
1
2
3
4
5
6
7
8
9
10
B
C
D
D
D
A
D
B
D
A
二、填空题(本大题共7小题,每小题4分,共28分)
11、y=8x-4 12、51 201 13、 14、(-3,4) 15、(1/e,+∞) 16、
17、
三、解答题:(本大题共7小题,共72分)
18、解:设乘火车去开会为事件A,乘轮船去开会为事件B,乘汽车去为事件C,乘飞机去为事件D,它们彼此互斥。……………………………2分
(1)P(A+D)=P(A)+P(D)=0.3+0.4=0.7……………………………6分
(2)P=1-P(B)=1-0.2=0.8……………………………10分
(3)P=0.5=0.2+0.3=0.1+0.4
21、(15分)解:⑴∵抛物线方程为,∴焦点,又直线过焦点,且垂直于x轴,∴的方程为,联立方程组,解得 ∴,。……………………………(6分)
⑵由⑴焦点,直线倾斜角为,直线的斜率,其方程为
,设,联立方程组
。∴,又,∴△OCD的面积为。……………(15分)
22、(Ⅰ)解:.
因为是的一个极值点,所以,即.
所以………………… 3分
设,其函数图象的开口向上.
由题意(*)式恒成立,
又.
即的取值范围是………………… 15分
解法二:由已知,得,即,
同课章节目录
