2.2.1 顺序结构与选择结构 同步测试(含答案)
文档属性
| 名称 | 2.2.1 顺序结构与选择结构 同步测试(含答案) | 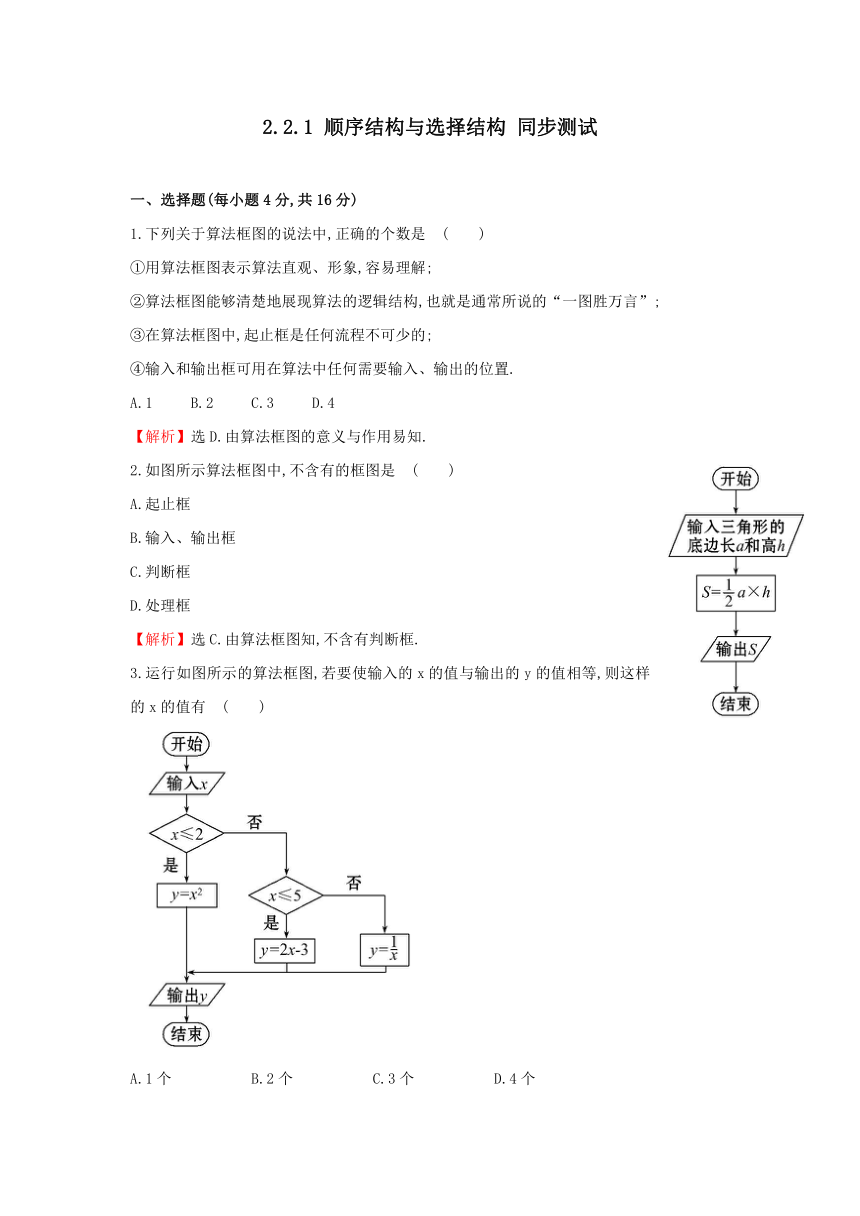 | |
| 格式 | zip | ||
| 文件大小 | 391.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-17 09:15:29 | ||
图片预览




文档简介
2.2.1
顺序结构与选择结构
同步测试
一、选择题(每小题4分,共16分)
1.下列关于算法框图的说法中,正确的个数是 ( )
①用算法框图表示算法直观、形象,容易理解;
②算法框图能够清楚地展现算法的逻辑结构,也就是通常所说的“一图胜万言”;
③在算法框图中,起止框是任何流程不可少的;
④输入和输出框可用在算法中任何需要输入、输出的位置.
A.1
B.2
C.3
D.4
【解析】选D.由算法框图的意义与作用易知.
2.如图所示算法框图中,不含有的框图是 ( )
A.起止框
B.输入、输出框
C.判断框
D.处理框
【解析】选C.由算法框图知,不含有判断框.
3.运行如图所示的算法框图,若要使输入的x的值与输出的y的值相等,则这样的x的值有 ( )
A.1个
B.2个
C.3个
D.4个
【解析】选C.当x≤2时,由x2=x得x=0或x=1,可以.
当2当x>5时,由=x得x=±1,舍去.
【举一反三】若输出的值为9,则输入的x的值为________.
【解析】当x≤2时,由x2=9,所以x=-3.
当2当x>5时,由=9,得x=,舍去.
答案:-3
4.如图所示的算法框图,能判断任意输入的数x的奇偶性,其中判断框内的条件是 ( )
A.m=0 B.x=0 C.x=1 D.m=1
【解析】选A.判断框中填写的应该是余数与0的关系,偶数即整数除以2的余数为0,而余数在这个算法框图中用字母m表示,所以判断框中应填写“m=0”.
二、填空题(每小题5分,共10分)
5.对任意非零实数a,b,若a b的运算原理如图所示,则e2ln
2 =________(e为自然对数的底数).
【解题指南】先分别求出e2ln2与的值,然后比较大小,选择下一步执行的语句,代入计算即可.
【解析】e2ln2=4,=8.
因为4<8,
执行输出b-1,
e2ln2 =7.
答案:7
6.已知函数f(x)=补充完成其求值的算法框图,则①处应填________.
【解析】由该算法框图的功能知①处应填x≤1.
答案:x≤1
【举一反三】若本题算法框图中“是”与“否”的位置互换,则①处应填________.
【解析】由该算法框图的功能知①处应填x>1.
答案:x>1
三、解答题(每小题12分,共24分)
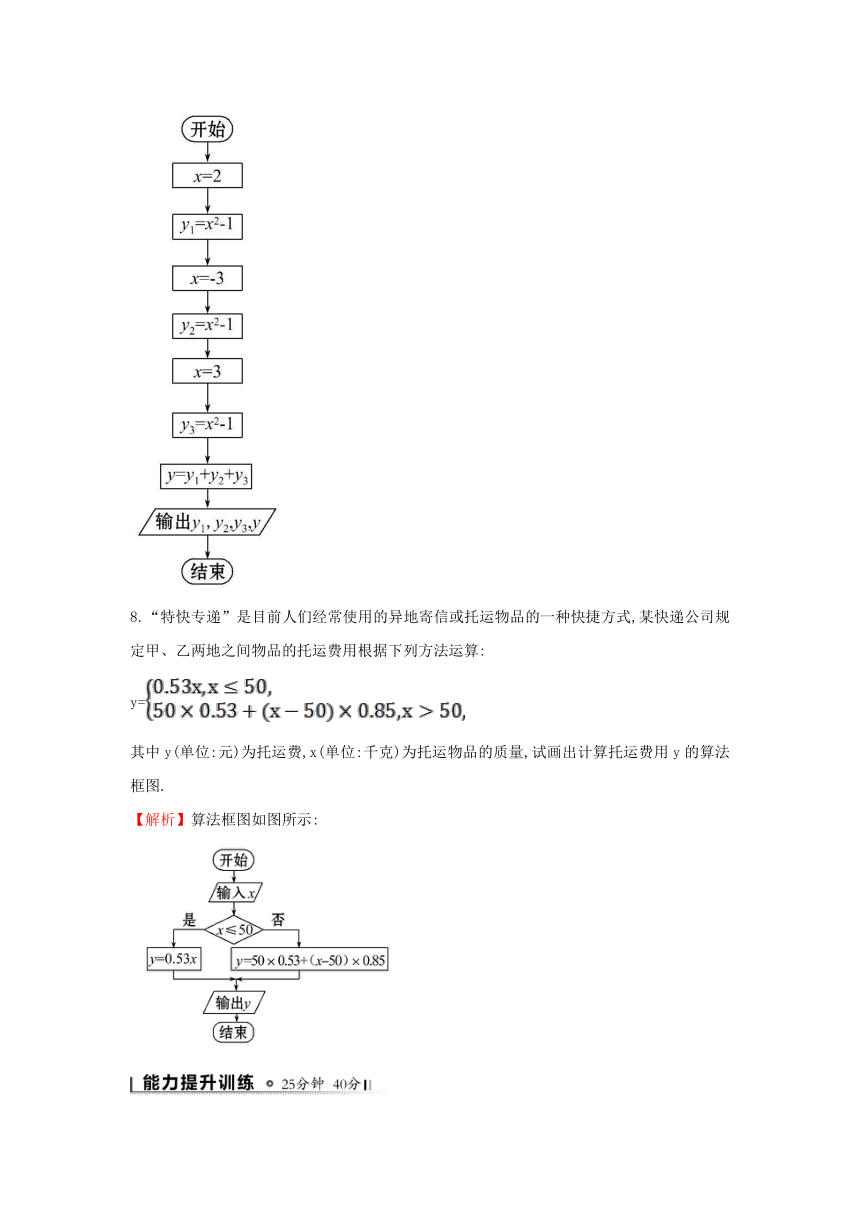
7.已知f(x)=x2-1,求f(2),f(-3),f(3),并计算f(2)+f(-3)+f(3)的值,设计出解决该问题的一个算法,并画出算法框图.
【解题指南】先求f(2),f(-3),f(3),写出算法,然后计算f(2)+f(-3)+f(3)的值利用赋值语句进行表示,最后根据算法画出相应的算法框图即可.
【解析】算法如下:
1.x=2.
2.y1=x2-1.
3.x=-3.
4.y2=x2-1.
5.x=3.
6.y3=x2-1.
7.y=y1+y2+y3.
8.输出y1,y2,y3,y.
算法框图:
8.“特快专递”是目前人们经常使用的异地寄信或托运物品的一种快捷方式,某快递公司规定甲、乙两地之间物品的托运费用根据下列方法运算:
y=
其中y(单位:元)为托运费,x(单位:千克)为托运物品的质量,试画出计算托运费用y的算法框图.
【解析】算法框图如图所示:
一、选择题(每小题4分,共12分)
1.下列关于选择结构的说法正确的是 ( )
A.无论选择结构中的条件满足与否,都只能执行两条路途之一
B.选择结构的两条路途可以同时执行
C.对于一个选择结构而言,判断框中的条件是唯一的
D.以上说法均不对
【解析】选A.选择结构虽然有2个出口,但每次只能走一个出口.
2.某算法框图如图所示,现输入如下四个函数,则可以输出的函数是 ( )
A.f(x)=x2
B.f(x)=
C.f(x)=lnx+2x-6
D.f(x)=x3+x
【解析】选D.由框图可知,当输入的函数f(x)为奇函数且存在零点时,才可输出f(x),由选项可知,仅f(x)=x3+x同时满足这两个条件,故选D.
【举一反三】若把判断框内条件“f(x)+f(-x)=0”改为“f(x)-f(-x)=0”,则结果如何
【解析】选A.因为f(x)-f(-x)=0,所以f(x)是偶函数.
因为f(x)=x2是偶函数且存在零点.
3.(2013·新课标全国卷Ⅰ)执行如图所示的算法框图,如果输入的t∈[-1,3],则输出的s属于 ( )
A.[-3,4]
B.[-5,2]
C.[-4,3]
D.[-2,5]
【解题指南】观察算法框图,知t<1对应的函数为s=3t,t≥1对应的函数为s=4t-t2,再结合函数的性质求出s的取值范围.
【解析】选A.由算法框图可知,s与t的关系可用分段函数表示为s=则s∈[-3,4].
二、填空题(每小题4分,共8分)
4.阅读如图的算法框图,若输入的a,b,c分别是sin30°,sin45°,sin60°,则输出的max=________.
【解析】由算法框图知,判断框中条件若成立,则将a赋给max,否则b较大,将b赋给max,第二个判断框原理也是取出最大值,此程序的功能是找出三数中的最大值,又sin60°=>sin45°=>sin30°=,所以最大值为sin60°.
答案:sin60°
5.某算法的算法框图如图所示,若输出结果为,则输入的实数x的值是________.
【解析】当x>1时,log2x=,所以x=可以,
当x≤1时,x-1=,x=舍去.
答案:
【变式训练】阅读如图所示的算法框图,若输出y的值为0,则输入x的值为________.
【解析】当x>1时,x2-4x+4=0得x=2.
当x<1时,x=0可以.
当x=1时,y=1舍去.
答案:0或2
三、解答题(每小题10分,共20分)
6.如图是判断“美数”的算法框图,在[30,40]内的所有整数中“美数”的个数是多少
【解析】由算法框图知美数是满足:能被3整除不能被6整除或能被12整除的数,在[30,40]内的所有整数中,所有的能被3整除的数有30,33,36,39,共有4个数,
在这四个数中能被12整除的有36,
在这四个数中不能被6整除的有33,39,
所以在[30,40]内的所有整数中“美数”的个数是3个.
7.某商场购物实行优惠措施,若购物金额x在800元以上的打8折,若购物金额x在600元以上且不超过800元时打9折,否则不打折,请设计出该商场打折优惠措施的算法框图.
【解析】根据题意,实际交款额y与购物金额x的函数关系式为:
y=
由函数的关系式可以知道,购物金额优惠措施可分为三种情况,故需用到条件结构设计算法.
算法框图如图所示:
【拓展提升】用条件结构解题的注意事项
(1)应用条件结构画算法框图应注意两点:一是需要判断的条件是什么,二是判断后的条件分别对应着什么样的结果.
(2)凡必须先根据条件作出判断,然后再决定进行哪一步骤的问题,在画算法框图时,必须引入判断框.
顺序结构与选择结构
同步测试
一、选择题(每小题4分,共16分)
1.下列关于算法框图的说法中,正确的个数是 ( )
①用算法框图表示算法直观、形象,容易理解;
②算法框图能够清楚地展现算法的逻辑结构,也就是通常所说的“一图胜万言”;
③在算法框图中,起止框是任何流程不可少的;
④输入和输出框可用在算法中任何需要输入、输出的位置.
A.1
B.2
C.3
D.4
【解析】选D.由算法框图的意义与作用易知.
2.如图所示算法框图中,不含有的框图是 ( )
A.起止框
B.输入、输出框
C.判断框
D.处理框
【解析】选C.由算法框图知,不含有判断框.
3.运行如图所示的算法框图,若要使输入的x的值与输出的y的值相等,则这样的x的值有 ( )
A.1个
B.2个
C.3个
D.4个
【解析】选C.当x≤2时,由x2=x得x=0或x=1,可以.
当2
【举一反三】若输出的值为9,则输入的x的值为________.
【解析】当x≤2时,由x2=9,所以x=-3.
当2
答案:-3
4.如图所示的算法框图,能判断任意输入的数x的奇偶性,其中判断框内的条件是 ( )
A.m=0 B.x=0 C.x=1 D.m=1
【解析】选A.判断框中填写的应该是余数与0的关系,偶数即整数除以2的余数为0,而余数在这个算法框图中用字母m表示,所以判断框中应填写“m=0”.
二、填空题(每小题5分,共10分)
5.对任意非零实数a,b,若a b的运算原理如图所示,则e2ln
2 =________(e为自然对数的底数).
【解题指南】先分别求出e2ln2与的值,然后比较大小,选择下一步执行的语句,代入计算即可.
【解析】e2ln2=4,=8.
因为4<8,
执行输出b-1,
e2ln2 =7.
答案:7
6.已知函数f(x)=补充完成其求值的算法框图,则①处应填________.
【解析】由该算法框图的功能知①处应填x≤1.
答案:x≤1
【举一反三】若本题算法框图中“是”与“否”的位置互换,则①处应填________.
【解析】由该算法框图的功能知①处应填x>1.
答案:x>1
三、解答题(每小题12分,共24分)
7.已知f(x)=x2-1,求f(2),f(-3),f(3),并计算f(2)+f(-3)+f(3)的值,设计出解决该问题的一个算法,并画出算法框图.
【解题指南】先求f(2),f(-3),f(3),写出算法,然后计算f(2)+f(-3)+f(3)的值利用赋值语句进行表示,最后根据算法画出相应的算法框图即可.
【解析】算法如下:
1.x=2.
2.y1=x2-1.
3.x=-3.
4.y2=x2-1.
5.x=3.
6.y3=x2-1.
7.y=y1+y2+y3.
8.输出y1,y2,y3,y.
算法框图:
8.“特快专递”是目前人们经常使用的异地寄信或托运物品的一种快捷方式,某快递公司规定甲、乙两地之间物品的托运费用根据下列方法运算:
y=
其中y(单位:元)为托运费,x(单位:千克)为托运物品的质量,试画出计算托运费用y的算法框图.
【解析】算法框图如图所示:
一、选择题(每小题4分,共12分)
1.下列关于选择结构的说法正确的是 ( )
A.无论选择结构中的条件满足与否,都只能执行两条路途之一
B.选择结构的两条路途可以同时执行
C.对于一个选择结构而言,判断框中的条件是唯一的
D.以上说法均不对
【解析】选A.选择结构虽然有2个出口,但每次只能走一个出口.
2.某算法框图如图所示,现输入如下四个函数,则可以输出的函数是 ( )
A.f(x)=x2
B.f(x)=
C.f(x)=lnx+2x-6
D.f(x)=x3+x
【解析】选D.由框图可知,当输入的函数f(x)为奇函数且存在零点时,才可输出f(x),由选项可知,仅f(x)=x3+x同时满足这两个条件,故选D.
【举一反三】若把判断框内条件“f(x)+f(-x)=0”改为“f(x)-f(-x)=0”,则结果如何
【解析】选A.因为f(x)-f(-x)=0,所以f(x)是偶函数.
因为f(x)=x2是偶函数且存在零点.
3.(2013·新课标全国卷Ⅰ)执行如图所示的算法框图,如果输入的t∈[-1,3],则输出的s属于 ( )
A.[-3,4]
B.[-5,2]
C.[-4,3]
D.[-2,5]
【解题指南】观察算法框图,知t<1对应的函数为s=3t,t≥1对应的函数为s=4t-t2,再结合函数的性质求出s的取值范围.
【解析】选A.由算法框图可知,s与t的关系可用分段函数表示为s=则s∈[-3,4].
二、填空题(每小题4分,共8分)
4.阅读如图的算法框图,若输入的a,b,c分别是sin30°,sin45°,sin60°,则输出的max=________.
【解析】由算法框图知,判断框中条件若成立,则将a赋给max,否则b较大,将b赋给max,第二个判断框原理也是取出最大值,此程序的功能是找出三数中的最大值,又sin60°=>sin45°=>sin30°=,所以最大值为sin60°.
答案:sin60°
5.某算法的算法框图如图所示,若输出结果为,则输入的实数x的值是________.
【解析】当x>1时,log2x=,所以x=可以,
当x≤1时,x-1=,x=舍去.
答案:
【变式训练】阅读如图所示的算法框图,若输出y的值为0,则输入x的值为________.
【解析】当x>1时,x2-4x+4=0得x=2.
当x<1时,x=0可以.
当x=1时,y=1舍去.
答案:0或2
三、解答题(每小题10分,共20分)
6.如图是判断“美数”的算法框图,在[30,40]内的所有整数中“美数”的个数是多少
【解析】由算法框图知美数是满足:能被3整除不能被6整除或能被12整除的数,在[30,40]内的所有整数中,所有的能被3整除的数有30,33,36,39,共有4个数,
在这四个数中能被12整除的有36,
在这四个数中不能被6整除的有33,39,
所以在[30,40]内的所有整数中“美数”的个数是3个.
7.某商场购物实行优惠措施,若购物金额x在800元以上的打8折,若购物金额x在600元以上且不超过800元时打9折,否则不打折,请设计出该商场打折优惠措施的算法框图.
【解析】根据题意,实际交款额y与购物金额x的函数关系式为:
y=
由函数的关系式可以知道,购物金额优惠措施可分为三种情况,故需用到条件结构设计算法.
算法框图如图所示:
【拓展提升】用条件结构解题的注意事项
(1)应用条件结构画算法框图应注意两点:一是需要判断的条件是什么,二是判断后的条件分别对应着什么样的结果.
(2)凡必须先根据条件作出判断,然后再决定进行哪一步骤的问题,在画算法框图时,必须引入判断框.
