2.2.1 顺序结构与选择结构 学案2(含答案)
文档属性
| 名称 | 2.2.1 顺序结构与选择结构 学案2(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 721.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-17 09:17:42 | ||
图片预览




文档简介
2.2.1 顺序结构与选择结构
学案
[读教材·填要点]
1.顺序结构
(1)定义:按照步骤依次执行的一个算法,称为具有“顺序结构”的算法,或者称为算法的顺序结构.
(2)算法框图:如图所示.
2.选择结构
(1)定义:在算法中,需要判断条件的真假,依据判断的结果决定后面的步骤,像这样的结构通常称为选择结构.
(2)算法框图:如图所示.
3.几个基本程序框、流程线和它们各自表示的功能
图形符号
名称
功能
终端框
(起止框)
表示一个算法的起始和结束
输入、输出框
表示一个算法输入和输出的信息
处理框(执行框)
赋值、计算
判断框
成立时标明“是”或“Y”;不成立时标明“否”或“N”
流程线
连接程序框
连接点
连接框图的两部分
[小问题·大思维]
1.顺序结构和选择结构有什么区别?
提示:选择结构不同于顺序结构的地方是:它不是依次执行,而是依据条件作出逻辑判断,选择执行不同指令中的一个.
2.什么问题适合用选择结构的框图进行设计?
提示:(1)凡根据条件先作出判断,再决定进行哪一个步骤的问题,在画程序框图时,必须引入判断,应用条件结构.如分段函数求值、数据的大小比较及含“若……则……”字样等问题.
(2)解决问题时的注意事项:常常先判断条件,再决定程序流向,菱形图有两个出口,但在最终执行程序时,选择的路线只能有一条.
[研一题]
[例1] 一次考试中,某同学的语文,数学,英语,物理,化学的成绩分别是a,b,c,d,e,设计一个计算该同学的总分和平均分的算法,并画出算法框图.
[自主解答] 算法步骤如下:
1.输入该同学的语文,数学,英语,物理,化学的成绩:a,b,c,d,e.
2.计算S=a+b+c+d+e.
3.计算W=.
4.输出S和W.
算法框图如图所示.
[悟一法]
顺序结构的执行顺序为从上到下依次进行.在画框图时要遵循以下原则:
(1)特定的符号表示特定的含义,不能随意创造;
(2)图形符号内的语言要精炼;
(3)框图的方向是自上而下或自左向右.
[通一类]
1.已知一个三角形三条边的边长分别为a,b,c,则三角形面积为S=,其中p=.请利用上述公式设计一个计算三角形面积的算法,并画出算法框图.
解:1.输入三角形三条边的长a,b,c.
2.计算p=.
3.计算S=.
4.输出S.
算法框图如图所示:
[研一题]
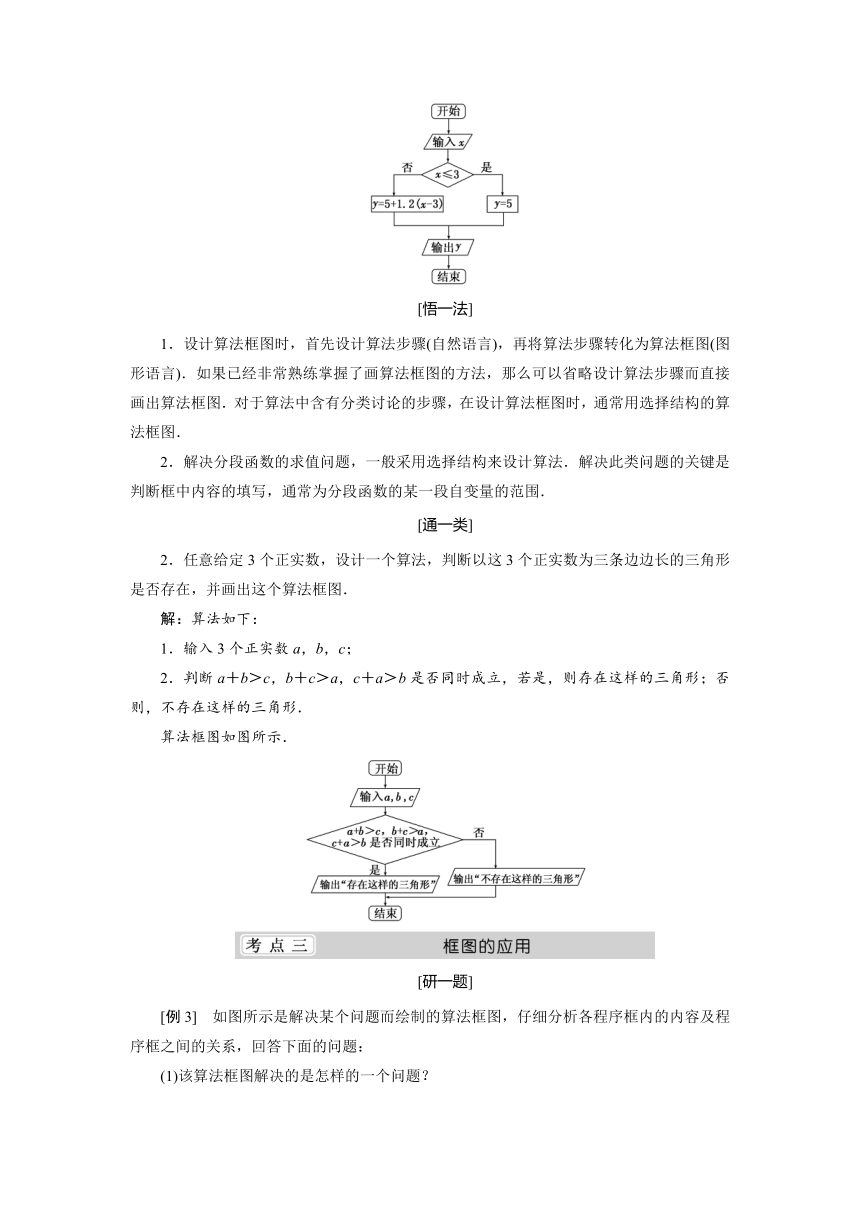
[例2] 某居民区的物业管理部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元,设计一个算法,根据输入的人数,计算应收取的卫生费,画出算法框图.
[自主解答] 设住户的人数为x,收取的卫生费为y元,依题意有y=这是一个分段函数求值问题,算法步骤如下:
1.输入x;
2.若x≤3,则y=5;否则y=5+1.2(x-3);
3.输出y.
算法框图如图:
[悟一法]
1.设计算法框图时,首先设计算法步骤(自然语言),再将算法步骤转化为算法框图(图形语言).如果已经非常熟练掌握了画算法框图的方法,那么可以省略设计算法步骤而直接画出算法框图.对于算法中含有分类讨论的步骤,在设计算法框图时,通常用选择结构的算法框图.
2.解决分段函数的求值问题,一般采用选择结构来设计算法.解决此类问题的关键是判断框中内容的填写,通常为分段函数的某一段自变量的范围.
[通一类]
2.任意给定3个正实数,设计一个算法,判断以这3个正实数为三条边边长的三角形是否存在,并画出这个算法框图.
解:算法如下:
1.输入3个正实数a,b,c;
2.判断a+b>c,b+c>a,c+a>b是否同时成立,若是,则存在这样的三角形;否则,不存在这样的三角形.
算法框图如图所示.
[研一题]
[例3] 如图所示是解决某个问题而绘制的算法框图,仔细分析各程序框内的内容及程序框之间的关系,回答下面的问题:
(1)该算法框图解决的是怎样的一个问题?
(2)若最终输出的结果y1=3,y2=-2,当x取5时输出的结果5a+b的值应该是多大?
(3)在(2)的前提下,输入的x值越大,输出的ax+b是不是越大?为什么?
(4)在(2)的前提下,当输入的x值为多大时,输出结果ax+b等于0
[自主解答] (1)该框图解决的是求函数f(x)=ax+b的函数值的问题.其中输入的是自变量x的值,输出的是x对应的函数值.
(2)y1=3,即2a+b=3
①
y2=-2,即-3a+b=-2
②
由①②得a=1,b=1.
∴f(x)=x+1.
∴当x取5时,5a+b=f(5)=5×1+1=6.
(3)输入的x值越大,输出的函数值ax+b越大,因为f(x)=x+1是R上的增函数.
(4)令f(x)=x+1=0,得x=-1,因而当输入的x值为-1时,输出的函数值为0.
[悟一法]
已知算法框图的函数问题,将框图所表示的算法翻译成自然语言,是由用自然语言表达的算法画出算法框图的逆向过程,对这两种语言的互译有助于熟练掌握算法的设计,而将算法框图翻译成自然语言相对而言比较陌生,是一个难点.
[通一类]
3.阅读算法框图,写出它表示的函数.
解:y=
如图,给出了一个算法框图,其作用是输入x的值,输出相应的y的值.若要使输入的x的值与输出的y的值相等,则这样的x的值有( )
A.1个
B.2个
C.3个
D.4个
[错解] 该算法框图的作用是求分段函数
y=的函数值.
(1)当x≤1时,令x2=x,得x=0或x=1.
(2)当1<x≤3时,令2x-3=x,得x=3.
(3)当x>3时,令=x,得x=±1均不满足x>3,故舍去.
综上,只有3个值符合.
[错因] 忽视分段函数定义域,而导致出错.
[正解] 该算法框图的作用是求分段函数
y=的函数值.
(1)当x≤1时,令x2=x,得x=0或x=1符合.
(2)当1<x<3时,令2x-3=x,得x=3,不符合,舍去.
(3)当x≥3时,令=x得x=±1,均不满足x≥3,故舍去.
综上可知,有2个值符合题意.
[答案] B
1.下列关于选择结构的说法中正确的是( )
A.对应的算法框图有一个入口和两个出口
B.对应的算法框图有两个入口和一个出口
C.算法框图中的两个出口可以同时执行
D.对于同一个算法来说,判断框中的条件是唯一的
答案:A
2.如图所示的算法框图,当输入x=2时,输出的结果是( )
A.4
B.5
C.6
D.13
解析:该算法框图的执行过程是:x=2,y=2×2+1=5,b=3×5-2=13,输出b=13.
答案:D
3.如图所示的算法框图,其功能是( )
A.输入a,b的值,按从小到大的顺序输出它们的值
B.输入a,b的值,按从大到小的顺序输出它们的值
C.求a,b中的最大值
D.求a,b中的最小值
解析:输入a=2,b=1,运行算法框图可得输出2,根据题意可知该算法框图的功能是输入a,b的值,输出它们中的最大值,即求a,b中的最大值.
答案:C
4.如图所示的框图,若a=5,则输出b=________.
解析:这是一个分段函数b=的求值问题.根据条件易知,b=52+1=26.
答案:26
5.阅读如图所示的框图,若输入x的值为2,则输出y的值为________.
解析:框图的实质是一个分段函数求值问题.
此分段函数为y=
若输入x=2,则应代入第一个式子,
则有y=x2-4x+4=4-8+4=0.
答案:0
6.“特快专递”是目前人们经常使用的异地邮寄信函或托运物品的一种快捷方式,某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算:
f=
其中f(单位:元)为托运费,ω为托运物品的重量(单位:千克),试画出计算费用f的算法框图.
解:
一、选择题
1.如图所示的选择结构,下列说法错误的是( )
A.当条件为假时,执行步骤甲
B.当条件为真时,执行步骤乙
C.无论条件是真是假,只能执行步骤甲和步骤乙中的一个
D.可能同时执行步骤甲和步骤乙
解析:步骤甲和乙不能同时执行.
答案:D
2.已知函数y=输入自变量x的值,求对应的函数值,设计算法框图时所含有的基本逻辑结构是( )
A.顺序结构
B.选择结构
C.顺序结构、选择结构
D.以上都不是
解析:任何算法框图中都有顺序结构,由于自变量在不同的范围内,有不同的对应法则,用选择结构.
答案:C
3.如图所示的算法框图,输入x=2,则输出的结果是( )
A.1
B.2
C.3
D.4
解析:输入x=2;则x=2>1,∴y==2,输出y=2.
答案:B
4.如图所示,算法框图运行的结果为s=( )
A.
B.
C.1
D.2
解析:由框图可知s=+=+=+2=.
答案:B
5.如图所示的算法框图中,当输入a1=3时,输出的b=7,则a2的值是( )
A.11
B.17
C.0.5
D.12
解析:b===7,∴a2=11.
答案:A
二、填空题
6.如图所示的算法功能是_____________________________________________.
答案:求两个实数a、b差的绝对值
7.已知函数y=如图是计算函数值y的算法框图,则在空白的判断框中应填________.
解析:由函数y=可知第一个判断框的否定条件为x≤0,第二个判断框的肯定条件的结果为y=0,因此空白判断框内应填“x=0”.
答案:x=0
8.阅读算法框图(如图所示),若a=50.6,b=0.65,c=log0.65,则输出的数是________.
解析:算法框图的功能是输出a,b,c中最大的数,又因为a>1,0<b<1,c<0,所以输出的数为50.6.
答案:50.6
三、解答题
9.已知函数y=写出求函数值的算法并画出算法框图.
解:算法如下:
1.输入x;
2.如果x>0,那么y=-1;如果x=0,那么y=0;如果x<0,那么y=1;
3.输出函数值y.
算法框图如图所示:
10.阅读如图所示的算法框图,根据该图和各问题的条件回答下面几个小题:
(1)该算法框图解决一个什么问题?
(2)若当输入的x值为0和4时,输出的值相等.问当输入的x值为3时,输出的值为多大?
(3)依据(2)的条件,要想使输出的值最大,输入x的值为多大?
解:(1)该算法框图是求二次函数y=-x2+mx的函数值.
(2)当输入的x值为0和4时,输出的值相等,即f(0)=f(4),可得m=4.∴f(x)=-x2+4x.∴f(3)=3.
(3)由(2),知f(x)=-x2+4x=-(x-2)2+4,
∴当输入的x值为2时,函数输出最大值4.
学案
[读教材·填要点]
1.顺序结构
(1)定义:按照步骤依次执行的一个算法,称为具有“顺序结构”的算法,或者称为算法的顺序结构.
(2)算法框图:如图所示.
2.选择结构
(1)定义:在算法中,需要判断条件的真假,依据判断的结果决定后面的步骤,像这样的结构通常称为选择结构.
(2)算法框图:如图所示.
3.几个基本程序框、流程线和它们各自表示的功能
图形符号
名称
功能
终端框
(起止框)
表示一个算法的起始和结束
输入、输出框
表示一个算法输入和输出的信息
处理框(执行框)
赋值、计算
判断框
成立时标明“是”或“Y”;不成立时标明“否”或“N”
流程线
连接程序框
连接点
连接框图的两部分
[小问题·大思维]
1.顺序结构和选择结构有什么区别?
提示:选择结构不同于顺序结构的地方是:它不是依次执行,而是依据条件作出逻辑判断,选择执行不同指令中的一个.
2.什么问题适合用选择结构的框图进行设计?
提示:(1)凡根据条件先作出判断,再决定进行哪一个步骤的问题,在画程序框图时,必须引入判断,应用条件结构.如分段函数求值、数据的大小比较及含“若……则……”字样等问题.
(2)解决问题时的注意事项:常常先判断条件,再决定程序流向,菱形图有两个出口,但在最终执行程序时,选择的路线只能有一条.
[研一题]
[例1] 一次考试中,某同学的语文,数学,英语,物理,化学的成绩分别是a,b,c,d,e,设计一个计算该同学的总分和平均分的算法,并画出算法框图.
[自主解答] 算法步骤如下:
1.输入该同学的语文,数学,英语,物理,化学的成绩:a,b,c,d,e.
2.计算S=a+b+c+d+e.
3.计算W=.
4.输出S和W.
算法框图如图所示.
[悟一法]
顺序结构的执行顺序为从上到下依次进行.在画框图时要遵循以下原则:
(1)特定的符号表示特定的含义,不能随意创造;
(2)图形符号内的语言要精炼;
(3)框图的方向是自上而下或自左向右.
[通一类]
1.已知一个三角形三条边的边长分别为a,b,c,则三角形面积为S=,其中p=.请利用上述公式设计一个计算三角形面积的算法,并画出算法框图.
解:1.输入三角形三条边的长a,b,c.
2.计算p=.
3.计算S=.
4.输出S.
算法框图如图所示:
[研一题]
[例2] 某居民区的物业管理部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元,设计一个算法,根据输入的人数,计算应收取的卫生费,画出算法框图.
[自主解答] 设住户的人数为x,收取的卫生费为y元,依题意有y=这是一个分段函数求值问题,算法步骤如下:
1.输入x;
2.若x≤3,则y=5;否则y=5+1.2(x-3);
3.输出y.
算法框图如图:
[悟一法]
1.设计算法框图时,首先设计算法步骤(自然语言),再将算法步骤转化为算法框图(图形语言).如果已经非常熟练掌握了画算法框图的方法,那么可以省略设计算法步骤而直接画出算法框图.对于算法中含有分类讨论的步骤,在设计算法框图时,通常用选择结构的算法框图.
2.解决分段函数的求值问题,一般采用选择结构来设计算法.解决此类问题的关键是判断框中内容的填写,通常为分段函数的某一段自变量的范围.
[通一类]
2.任意给定3个正实数,设计一个算法,判断以这3个正实数为三条边边长的三角形是否存在,并画出这个算法框图.
解:算法如下:
1.输入3个正实数a,b,c;
2.判断a+b>c,b+c>a,c+a>b是否同时成立,若是,则存在这样的三角形;否则,不存在这样的三角形.
算法框图如图所示.
[研一题]
[例3] 如图所示是解决某个问题而绘制的算法框图,仔细分析各程序框内的内容及程序框之间的关系,回答下面的问题:
(1)该算法框图解决的是怎样的一个问题?
(2)若最终输出的结果y1=3,y2=-2,当x取5时输出的结果5a+b的值应该是多大?
(3)在(2)的前提下,输入的x值越大,输出的ax+b是不是越大?为什么?
(4)在(2)的前提下,当输入的x值为多大时,输出结果ax+b等于0
[自主解答] (1)该框图解决的是求函数f(x)=ax+b的函数值的问题.其中输入的是自变量x的值,输出的是x对应的函数值.
(2)y1=3,即2a+b=3
①
y2=-2,即-3a+b=-2
②
由①②得a=1,b=1.
∴f(x)=x+1.
∴当x取5时,5a+b=f(5)=5×1+1=6.
(3)输入的x值越大,输出的函数值ax+b越大,因为f(x)=x+1是R上的增函数.
(4)令f(x)=x+1=0,得x=-1,因而当输入的x值为-1时,输出的函数值为0.
[悟一法]
已知算法框图的函数问题,将框图所表示的算法翻译成自然语言,是由用自然语言表达的算法画出算法框图的逆向过程,对这两种语言的互译有助于熟练掌握算法的设计,而将算法框图翻译成自然语言相对而言比较陌生,是一个难点.
[通一类]
3.阅读算法框图,写出它表示的函数.
解:y=
如图,给出了一个算法框图,其作用是输入x的值,输出相应的y的值.若要使输入的x的值与输出的y的值相等,则这样的x的值有( )
A.1个
B.2个
C.3个
D.4个
[错解] 该算法框图的作用是求分段函数
y=的函数值.
(1)当x≤1时,令x2=x,得x=0或x=1.
(2)当1<x≤3时,令2x-3=x,得x=3.
(3)当x>3时,令=x,得x=±1均不满足x>3,故舍去.
综上,只有3个值符合.
[错因] 忽视分段函数定义域,而导致出错.
[正解] 该算法框图的作用是求分段函数
y=的函数值.
(1)当x≤1时,令x2=x,得x=0或x=1符合.
(2)当1<x<3时,令2x-3=x,得x=3,不符合,舍去.
(3)当x≥3时,令=x得x=±1,均不满足x≥3,故舍去.
综上可知,有2个值符合题意.
[答案] B
1.下列关于选择结构的说法中正确的是( )
A.对应的算法框图有一个入口和两个出口
B.对应的算法框图有两个入口和一个出口
C.算法框图中的两个出口可以同时执行
D.对于同一个算法来说,判断框中的条件是唯一的
答案:A
2.如图所示的算法框图,当输入x=2时,输出的结果是( )
A.4
B.5
C.6
D.13
解析:该算法框图的执行过程是:x=2,y=2×2+1=5,b=3×5-2=13,输出b=13.
答案:D
3.如图所示的算法框图,其功能是( )
A.输入a,b的值,按从小到大的顺序输出它们的值
B.输入a,b的值,按从大到小的顺序输出它们的值
C.求a,b中的最大值
D.求a,b中的最小值
解析:输入a=2,b=1,运行算法框图可得输出2,根据题意可知该算法框图的功能是输入a,b的值,输出它们中的最大值,即求a,b中的最大值.
答案:C
4.如图所示的框图,若a=5,则输出b=________.
解析:这是一个分段函数b=的求值问题.根据条件易知,b=52+1=26.
答案:26
5.阅读如图所示的框图,若输入x的值为2,则输出y的值为________.
解析:框图的实质是一个分段函数求值问题.
此分段函数为y=
若输入x=2,则应代入第一个式子,
则有y=x2-4x+4=4-8+4=0.
答案:0
6.“特快专递”是目前人们经常使用的异地邮寄信函或托运物品的一种快捷方式,某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算:
f=
其中f(单位:元)为托运费,ω为托运物品的重量(单位:千克),试画出计算费用f的算法框图.
解:
一、选择题
1.如图所示的选择结构,下列说法错误的是( )
A.当条件为假时,执行步骤甲
B.当条件为真时,执行步骤乙
C.无论条件是真是假,只能执行步骤甲和步骤乙中的一个
D.可能同时执行步骤甲和步骤乙
解析:步骤甲和乙不能同时执行.
答案:D
2.已知函数y=输入自变量x的值,求对应的函数值,设计算法框图时所含有的基本逻辑结构是( )
A.顺序结构
B.选择结构
C.顺序结构、选择结构
D.以上都不是
解析:任何算法框图中都有顺序结构,由于自变量在不同的范围内,有不同的对应法则,用选择结构.
答案:C
3.如图所示的算法框图,输入x=2,则输出的结果是( )
A.1
B.2
C.3
D.4
解析:输入x=2;则x=2>1,∴y==2,输出y=2.
答案:B
4.如图所示,算法框图运行的结果为s=( )
A.
B.
C.1
D.2
解析:由框图可知s=+=+=+2=.
答案:B
5.如图所示的算法框图中,当输入a1=3时,输出的b=7,则a2的值是( )
A.11
B.17
C.0.5
D.12
解析:b===7,∴a2=11.
答案:A
二、填空题
6.如图所示的算法功能是_____________________________________________.
答案:求两个实数a、b差的绝对值
7.已知函数y=如图是计算函数值y的算法框图,则在空白的判断框中应填________.
解析:由函数y=可知第一个判断框的否定条件为x≤0,第二个判断框的肯定条件的结果为y=0,因此空白判断框内应填“x=0”.
答案:x=0
8.阅读算法框图(如图所示),若a=50.6,b=0.65,c=log0.65,则输出的数是________.
解析:算法框图的功能是输出a,b,c中最大的数,又因为a>1,0<b<1,c<0,所以输出的数为50.6.
答案:50.6
三、解答题
9.已知函数y=写出求函数值的算法并画出算法框图.
解:算法如下:
1.输入x;
2.如果x>0,那么y=-1;如果x=0,那么y=0;如果x<0,那么y=1;
3.输出函数值y.
算法框图如图所示:
10.阅读如图所示的算法框图,根据该图和各问题的条件回答下面几个小题:
(1)该算法框图解决一个什么问题?
(2)若当输入的x值为0和4时,输出的值相等.问当输入的x值为3时,输出的值为多大?
(3)依据(2)的条件,要想使输出的值最大,输入x的值为多大?
解:(1)该算法框图是求二次函数y=-x2+mx的函数值.
(2)当输入的x值为0和4时,输出的值相等,即f(0)=f(4),可得m=4.∴f(x)=-x2+4x.∴f(3)=3.
(3)由(2),知f(x)=-x2+4x=-(x-2)2+4,
∴当输入的x值为2时,函数输出最大值4.
