2.2.2 变量与赋值 课后作业(含答案)
文档属性
| 名称 | 2.2.2 变量与赋值 课后作业(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 266.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-17 00:00:00 | ||
图片预览


文档简介
2.2.2
变量与赋值
课后作业
课时目标 掌握变量及赋值的含义,会应用赋值语句.
1.变量:在研究问题的过程中__________________的量称为变量.
2.赋值语句的格式:变量=表达式.
一、选择题
1.给出下列算法框图
若输出的结果为2,则①处的处理框内应填的是( )
A.x=2
B.b=2
C.x=1
D.a=5
2.下列所示的算法框图输出的结果为( )
A.2,5
B.4,5
C.11,5
D.7,5
3.下列给出的赋值语句中正确的是( )
A.4=M
B.M=-M
C.B=A=3
D.x+y=0
4.
如图所示的算法框图表示的算法意义是( )
A.求边长为3,4,5的直角三角形面积
B.求边长为3,4,5的直角三角形内切圆面积
C.求边长为3,4,5的直角三角形外接圆面积
D.求以3,4,5为弦的圆面积
5.算法框图描述的算法的运行结果是( )
A.-5
B.5
C.-1
D.-2
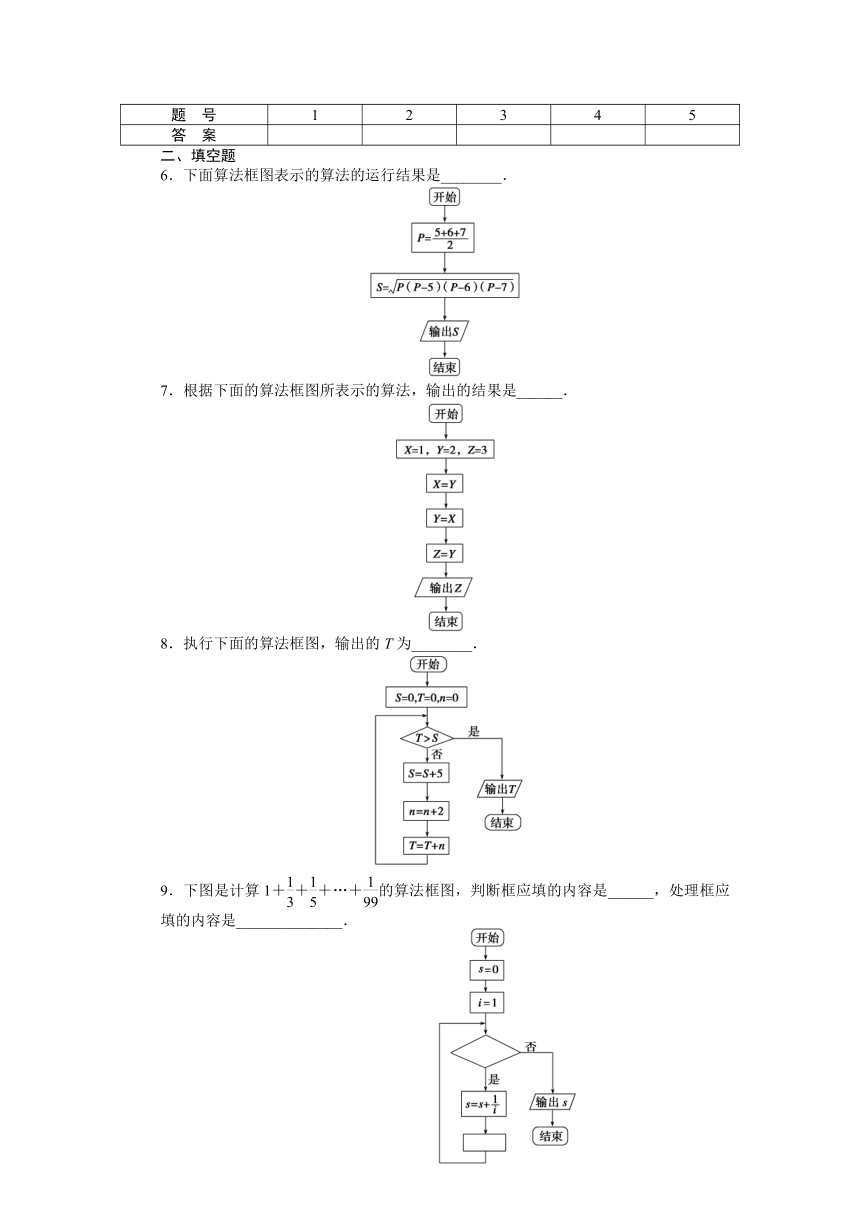
题 号
1
2
3
4
5
答 案
二、填空题
6.下面算法框图表示的算法的运行结果是________.
7.根据下面的算法框图所表示的算法,输出的结果是______.
8.执行下面的算法框图,输出的T为________.
9.下图是计算1+++…+的算法框图,判断框应填的内容是______,处理框应填的内容是______________.
三、解答题
10.已知半径为r的圆的周长公式为C=2πr,当r=10时,写出计算圆的周长的一个算法,并画出算法框图.
11.已知函数y=2x+3,设计一个算法,若给出函数图象上任一点的横坐标x(由键盘输入),求该点到坐标原点的距离,并画出算法框图.
能力提升
12.已知f(x)=x2-2x-3.画出求f(3)、f(-5)、f(5)的值的一个算法框图.
13.如图所示的算法框图,当输入的x的值为0和4时,输出的值相等,根据该图和下列各小题的条件回答下面的几个问题.
(1)该算法框图解决的是一个什么问题?
(2)当输入的x的值为3时,输出的f(x)的值为多大?
(3)要想使输出的值最大,输入的x的值应为多大?
(4)按照这个算法框图输出的f(x)值,当x的值大于2时,x值大的输出的f(x)值反而小,为什么?
(5)要想使输出的值等于3,输入的x的值应为多大?
(6)要想使输入的值与输出的值相等,输入的x的值应为多大?
1.赋值语句是最重要的一种基本语句,也是一个算法必不可少的重要组成部分,使用赋值语句,一定要注意其格式要求,如:赋值号左边只能是变量而不能是表达式;赋值号左右两边不能对换;不能利用赋值语句进行代数式计算等.
2.利用赋值语句可以实现两个变量值的互换,方法是引进第三个变量,用三个赋值语句完成.
2.2.2
变量与赋值
答案
知识梳理
1.可以取不同数值
作业设计
1.C [因结果是b=2,∴2=a-3,即a=5.当2x+3=5时,得x=1.]
2.C
3.B [赋值语句的格式为:变量=表达式,是将右边表达式的值赋给左边的变量,赋值时左右两端不能对换,也不能进行字符运算.故选B.]
4.B [直角三角形内切圆半径r=.]
5.A
6.6
解析 由题意P==9,S===6.
7.2
解析 该算法的第1步分别将X,Y,Z赋于1,2,3三个数,第2步使X取Y的值,即X取值变成2,第3步使Y取X的值,即Y的值也是2,第4步让Z取Y的值,即Z取值也是2,从而第5步输出时,Z的值是2.
8.30
解析 按照算法框图依次执行为
S=5,n=2,T=2;
S=10,n=4,T=2+4=6;
S=15,n=6,T=6+6=12;
S=20,n=8,T=12+8=20;
S=25,n=10,T=20+10=30>S,输出T=30.
9.i≤99 i=i+2
解析 由题意知,该算法从i=1开始到99结束,循环变量依次加2.
10.解 算法如下:
第一步,令r=10.
第二步,计算C=2πr,
第三步,输出C.
算法框图:
11.解 算法如下:
第一步,输入横坐标的值x.
第二步,计算y=2x+3.
第三步,计算d=.
第四步,输出d.
算法框图如图:
12.解 算法框图如下:
13.解 (1)该算法框图解决的是求二次函数f(x)=-x2+mx的函数值的问题.
(2)当输入的x的值为0和4时,输出的值相等,
即f(0)=f(4).
因为f(0)=0,f(4)=-16+4m,
所以-16+4m=0,所以m=4.
所以f(x)=-x2+4x.
因为f(3)=-32+4×3=3,
所以当输入的x的值为3时,
输出的f(x)的值为3.
(3)因为f(x)=-x2+4x=-(x-2)2+4,
当x=2时,f(x)max=4,
所以要想使输出的值最大,输入的x的值应为2.
(4)因为f(x)=-(x-2)2+4,
所以函数f(x)在[2,+∞)上是减函数.
所以在[2,+∞)上,x值大的对应的函数值反而小,
从而当输入的x的值大于2时,x值大的输出的f(x)值反而小.
(5)令f(x)=-x2+4x=3,解得x=1或x=3,
所以要想使输出的值等于3,
输入的x的值应为1或3.
(6)由f(x)=x,即-x2+4x=x,得x=0或x=3,
所以要想使输入的值和输出的值相等,输入的x的值应为0或3.
变量与赋值
课后作业
课时目标 掌握变量及赋值的含义,会应用赋值语句.
1.变量:在研究问题的过程中__________________的量称为变量.
2.赋值语句的格式:变量=表达式.
一、选择题
1.给出下列算法框图
若输出的结果为2,则①处的处理框内应填的是( )
A.x=2
B.b=2
C.x=1
D.a=5
2.下列所示的算法框图输出的结果为( )
A.2,5
B.4,5
C.11,5
D.7,5
3.下列给出的赋值语句中正确的是( )
A.4=M
B.M=-M
C.B=A=3
D.x+y=0
4.
如图所示的算法框图表示的算法意义是( )
A.求边长为3,4,5的直角三角形面积
B.求边长为3,4,5的直角三角形内切圆面积
C.求边长为3,4,5的直角三角形外接圆面积
D.求以3,4,5为弦的圆面积
5.算法框图描述的算法的运行结果是( )
A.-5
B.5
C.-1
D.-2
题 号
1
2
3
4
5
答 案
二、填空题
6.下面算法框图表示的算法的运行结果是________.
7.根据下面的算法框图所表示的算法,输出的结果是______.
8.执行下面的算法框图,输出的T为________.
9.下图是计算1+++…+的算法框图,判断框应填的内容是______,处理框应填的内容是______________.
三、解答题
10.已知半径为r的圆的周长公式为C=2πr,当r=10时,写出计算圆的周长的一个算法,并画出算法框图.
11.已知函数y=2x+3,设计一个算法,若给出函数图象上任一点的横坐标x(由键盘输入),求该点到坐标原点的距离,并画出算法框图.
能力提升
12.已知f(x)=x2-2x-3.画出求f(3)、f(-5)、f(5)的值的一个算法框图.
13.如图所示的算法框图,当输入的x的值为0和4时,输出的值相等,根据该图和下列各小题的条件回答下面的几个问题.
(1)该算法框图解决的是一个什么问题?
(2)当输入的x的值为3时,输出的f(x)的值为多大?
(3)要想使输出的值最大,输入的x的值应为多大?
(4)按照这个算法框图输出的f(x)值,当x的值大于2时,x值大的输出的f(x)值反而小,为什么?
(5)要想使输出的值等于3,输入的x的值应为多大?
(6)要想使输入的值与输出的值相等,输入的x的值应为多大?
1.赋值语句是最重要的一种基本语句,也是一个算法必不可少的重要组成部分,使用赋值语句,一定要注意其格式要求,如:赋值号左边只能是变量而不能是表达式;赋值号左右两边不能对换;不能利用赋值语句进行代数式计算等.
2.利用赋值语句可以实现两个变量值的互换,方法是引进第三个变量,用三个赋值语句完成.
2.2.2
变量与赋值
答案
知识梳理
1.可以取不同数值
作业设计
1.C [因结果是b=2,∴2=a-3,即a=5.当2x+3=5时,得x=1.]
2.C
3.B [赋值语句的格式为:变量=表达式,是将右边表达式的值赋给左边的变量,赋值时左右两端不能对换,也不能进行字符运算.故选B.]
4.B [直角三角形内切圆半径r=.]
5.A
6.6
解析 由题意P==9,S===6.
7.2
解析 该算法的第1步分别将X,Y,Z赋于1,2,3三个数,第2步使X取Y的值,即X取值变成2,第3步使Y取X的值,即Y的值也是2,第4步让Z取Y的值,即Z取值也是2,从而第5步输出时,Z的值是2.
8.30
解析 按照算法框图依次执行为
S=5,n=2,T=2;
S=10,n=4,T=2+4=6;
S=15,n=6,T=6+6=12;
S=20,n=8,T=12+8=20;
S=25,n=10,T=20+10=30>S,输出T=30.
9.i≤99 i=i+2
解析 由题意知,该算法从i=1开始到99结束,循环变量依次加2.
10.解 算法如下:
第一步,令r=10.
第二步,计算C=2πr,
第三步,输出C.
算法框图:
11.解 算法如下:
第一步,输入横坐标的值x.
第二步,计算y=2x+3.
第三步,计算d=.
第四步,输出d.
算法框图如图:
12.解 算法框图如下:
13.解 (1)该算法框图解决的是求二次函数f(x)=-x2+mx的函数值的问题.
(2)当输入的x的值为0和4时,输出的值相等,
即f(0)=f(4).
因为f(0)=0,f(4)=-16+4m,
所以-16+4m=0,所以m=4.
所以f(x)=-x2+4x.
因为f(3)=-32+4×3=3,
所以当输入的x的值为3时,
输出的f(x)的值为3.
(3)因为f(x)=-x2+4x=-(x-2)2+4,
当x=2时,f(x)max=4,
所以要想使输出的值最大,输入的x的值应为2.
(4)因为f(x)=-(x-2)2+4,
所以函数f(x)在[2,+∞)上是减函数.
所以在[2,+∞)上,x值大的对应的函数值反而小,
从而当输入的x的值大于2时,x值大的输出的f(x)值反而小.
(5)令f(x)=-x2+4x=3,解得x=1或x=3,
所以要想使输出的值等于3,
输入的x的值应为1或3.
(6)由f(x)=x,即-x2+4x=x,得x=0或x=3,
所以要想使输入的值和输出的值相等,输入的x的值应为0或3.
