2.2.3 循环结构 课时检测(含答案)
文档属性
| 名称 | 2.2.3 循环结构 课时检测(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 392.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-17 00:00:00 | ||
图片预览


文档简介
2.2.3
循环结构
课时检测
一、选择题
1.下列结构中组成算法的结构的个数有( )
①顺序结构 ②选择结构 ③循环结构 ④输入结构 ⑤输出结构
A.2
B.3
C.4
D.5
[答案] B
[解析] 组成算法的结构有顺序结构、选择结构和循环结构共三种.
2.如图所示,该程序运行后输出的结果为( )
A.7
B.15
C.31
D.63
[答案] D
[解析] A=1,S=2×1+1=3;
A=2,S=2×3+1=7;
A=3,S=2×7+1=15;
A=4,S=2×15+1=31;
A=5,S=2×31+1=63;
A=6>5,输出S=63.
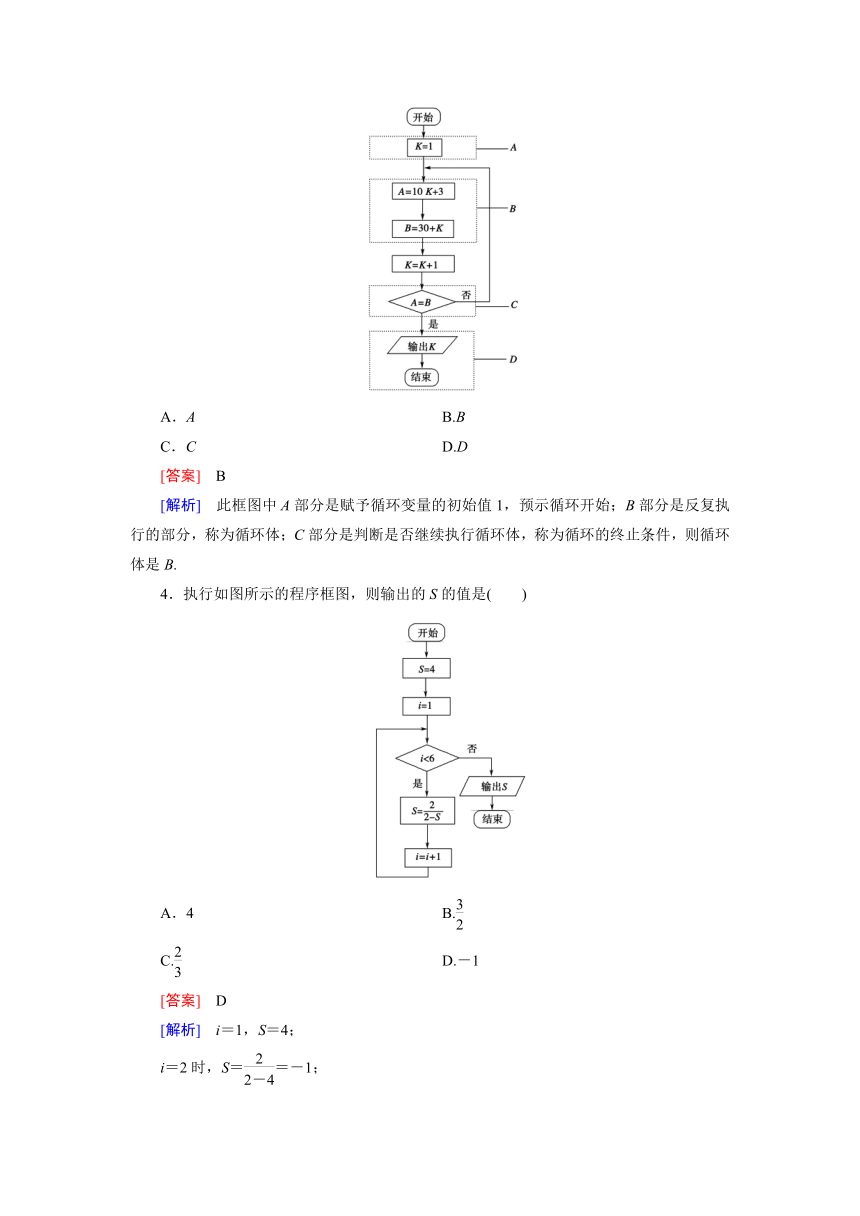
3.框图(如下图)中的循环体是( )
A.A
B.B
C.C
D.D
[答案] B
[解析] 此框图中A部分是赋予循环变量的初始值1,预示循环开始;B部分是反复执行的部分,称为循环体;C部分是判断是否继续执行循环体,称为循环的终止条件,则循环体是B.
4.执行如图所示的程序框图,则输出的S的值是( )
A.4
B.
C.
D.-1
[答案] D
[解析] i=1,S=4;
i=2时,S==-1;
i=3时,S==;
i=4时,S==;i=5时,S==4;
i=6时,S==-1,
此时跳出循环,输出S的值-1.
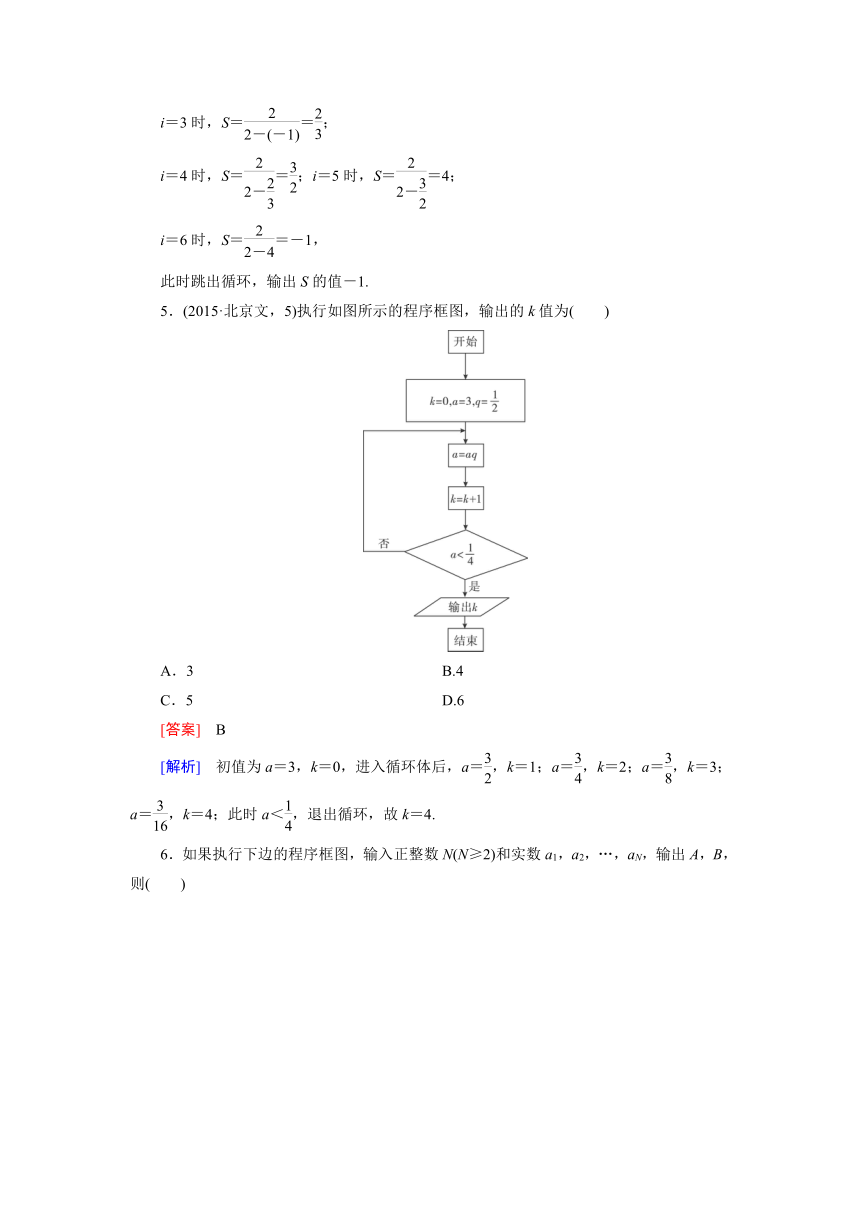
5.(2015·北京文,5)执行如图所示的程序框图,输出的k值为( )
A.3
B.4
C.5
D.6
[答案] B
[解析] 初值为a=3,k=0,进入循环体后,a=,k=1;a=,k=2;a=,k=3;a=,k=4;此时a<,退出循环,故k=4.
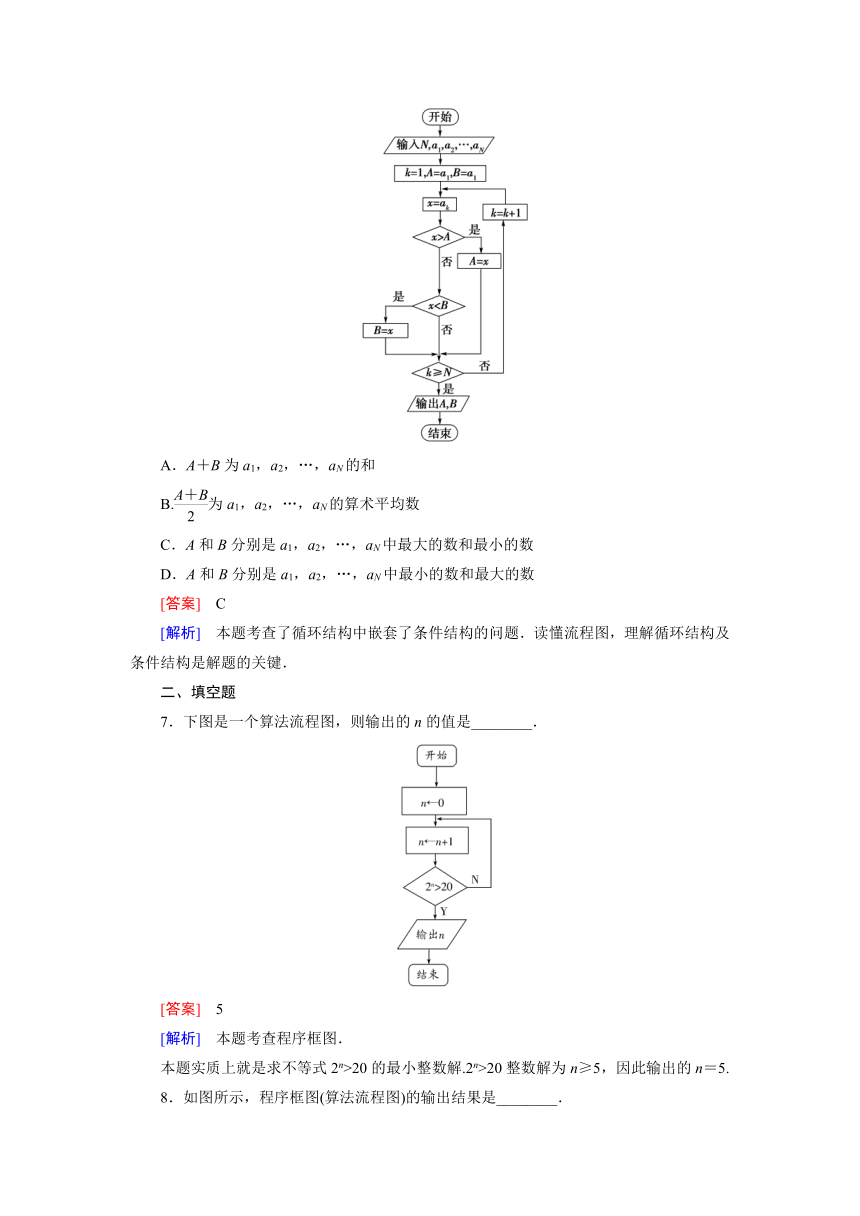
6.如果执行下边的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )
A.A+B为a1,a2,…,aN的和
B.为a1,a2,…,aN的算术平均数
C.A和B分别是a1,a2,…,aN中最大的数和最小的数
D.A和B分别是a1,a2,…,aN中最小的数和最大的数
[答案] C
[解析] 本题考查了循环结构中嵌套了条件结构的问题.读懂流程图,理解循环结构及条件结构是解题的关键.
二、填空题
7.下图是一个算法流程图,则输出的n的值是________.
[答案] 5
[解析] 本题考查程序框图.
本题实质上就是求不等式2n>20的最小整数解.2n>20整数解为n≥5,因此输出的n=5.
8.如图所示,程序框图(算法流程图)的输出结果是________.
[答案] 15
[解析] 该题考查算法程序框图的循环结构.
∵T=0+1+2+…+14=(1+14)×7=15×7=105,
此时k=14,再循环一次终止,
∴k=15.
三、解答题
9.设计一个计算2+4+6+…+100的值的算法,并画出算法框图.
[解析] 算法如下:
1.S=0.
2.i=2.
3.S=S+i.
4.i=i+2.
5.如果i大于100,则执行6,否则执行3,4.
6.输出S.
算法流程图如下图所示.
10.设计算法,输出1
000以内能同时被3和5整除的所有正整数,画出算法的流程图.
[解析] 算法如下:
1.n=1.
2.a=15n,输出a.
3.n=n+1.
4.若n>66,则执行5,否则执行2,3.
5.结束.
6.算法流程图如下图:
一、选择题
1.阅读如下程序框图,运行相应的程序,则程序运行后输出的结果为( )
A.7
B.9
C.10
D.11
[答案] B
[解析] 本题主要考查循环结构的程序框图,由框图运行程序我们可知.
第①步,运行i=1,S=0+lg=lg>-1
第②步,i=3,S=lg+lg=lg>-1
第③步,
i=5,S=lg+lg=lg>-1
第④步,i=7,S=lg+lg=lg>-1
第⑤步,i=9,S=lg+lg=lg<-1
程序框图结束此时输出i=9,故选B,本题解题关键①是找到对数的运算规律,②要掌握好每执行一步程序,i与S的函代关系.
2.执行下面的程序框图,如果输入a=4,那么输出的n的值为( )
A.2
B.3
C.4
D.5
[答案] B
[解析] 本题考查了算法循环结构的直到型的流程图问题.n=0,p=0+40=1,q=2+1=3;
n=1,p=1+41=5,q=6+1=7;
n=2,p=5+42=21,q=14+1=15,n=3,p>q.
算法的考查多以流程图的形式出现,重点考查的是循环结构.
二、填空题
3.阅读如下图所示的算法框图,若输入m=4,n=3,则输出a=________,i=________.
[答案] 6 2
[解析] 该算法框图的执行过程是:
m=4
n=3
i=1
a=4+1=5
3整除5 否
i=1+1=2
a=4+2=6
3整除6 是
输出a=6,i=2.
4.(2015·山东文,11)执行下边的程序框图,若输入的x的值为1,则输出的y的值是________.
[答案] 13
[解析] 第一次执行程序,满足条件x<2,x=1+1=2;第二次执行程序,不满足条件x<2,y=3×22+1=13,输出y=13,结束.答案为13.
三、解答题
5.画出求(共6个2)的值的算法的流程图.
[分析] 这个式子实际上是求和,取倒数;再求和,取倒数;反复五次即达到目的.第一个和为2+.
[解析] 流程图如下图所示.
6.用N1代表第一个学生的学号,Ni代表第i个学生的学号,Gi代表第i个学生的成绩,那么如图,表示一个什么样的算法?
[解析] 算法:
第一步:i=1;
第二步:如果Gi≥90,则输出Ni,Gi,否则直接转到第三步;
第三步:i=i+1;
第四步:如果i≤60,则执行第二步,重复执行第二步、第三步、第四步,否则结束.
故该框图表示的算法功能是:输出60名学生中分数在90分或90分以上的学生的学号和成绩.
7.设计一个计算20个数的平均数的算法,并画出相应的流程图.
[解析] 算法如下.
1 S=0.
2 i=1.
3 输入G.
4 S=S+G.
5 i=i+1.
6 如果i不大于20,转3;如果i大于20,退出循环.
7 A=.
8 输出A.
流程图如下图所示.
循环结构
课时检测
一、选择题
1.下列结构中组成算法的结构的个数有( )
①顺序结构 ②选择结构 ③循环结构 ④输入结构 ⑤输出结构
A.2
B.3
C.4
D.5
[答案] B
[解析] 组成算法的结构有顺序结构、选择结构和循环结构共三种.
2.如图所示,该程序运行后输出的结果为( )
A.7
B.15
C.31
D.63
[答案] D
[解析] A=1,S=2×1+1=3;
A=2,S=2×3+1=7;
A=3,S=2×7+1=15;
A=4,S=2×15+1=31;
A=5,S=2×31+1=63;
A=6>5,输出S=63.
3.框图(如下图)中的循环体是( )
A.A
B.B
C.C
D.D
[答案] B
[解析] 此框图中A部分是赋予循环变量的初始值1,预示循环开始;B部分是反复执行的部分,称为循环体;C部分是判断是否继续执行循环体,称为循环的终止条件,则循环体是B.
4.执行如图所示的程序框图,则输出的S的值是( )
A.4
B.
C.
D.-1
[答案] D
[解析] i=1,S=4;
i=2时,S==-1;
i=3时,S==;
i=4时,S==;i=5时,S==4;
i=6时,S==-1,
此时跳出循环,输出S的值-1.
5.(2015·北京文,5)执行如图所示的程序框图,输出的k值为( )
A.3
B.4
C.5
D.6
[答案] B
[解析] 初值为a=3,k=0,进入循环体后,a=,k=1;a=,k=2;a=,k=3;a=,k=4;此时a<,退出循环,故k=4.
6.如果执行下边的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )
A.A+B为a1,a2,…,aN的和
B.为a1,a2,…,aN的算术平均数
C.A和B分别是a1,a2,…,aN中最大的数和最小的数
D.A和B分别是a1,a2,…,aN中最小的数和最大的数
[答案] C
[解析] 本题考查了循环结构中嵌套了条件结构的问题.读懂流程图,理解循环结构及条件结构是解题的关键.
二、填空题
7.下图是一个算法流程图,则输出的n的值是________.
[答案] 5
[解析] 本题考查程序框图.
本题实质上就是求不等式2n>20的最小整数解.2n>20整数解为n≥5,因此输出的n=5.
8.如图所示,程序框图(算法流程图)的输出结果是________.
[答案] 15
[解析] 该题考查算法程序框图的循环结构.
∵T=0+1+2+…+14=(1+14)×7=15×7=105,
此时k=14,再循环一次终止,
∴k=15.
三、解答题
9.设计一个计算2+4+6+…+100的值的算法,并画出算法框图.
[解析] 算法如下:
1.S=0.
2.i=2.
3.S=S+i.
4.i=i+2.
5.如果i大于100,则执行6,否则执行3,4.
6.输出S.
算法流程图如下图所示.
10.设计算法,输出1
000以内能同时被3和5整除的所有正整数,画出算法的流程图.
[解析] 算法如下:
1.n=1.
2.a=15n,输出a.
3.n=n+1.
4.若n>66,则执行5,否则执行2,3.
5.结束.
6.算法流程图如下图:
一、选择题
1.阅读如下程序框图,运行相应的程序,则程序运行后输出的结果为( )
A.7
B.9
C.10
D.11
[答案] B
[解析] 本题主要考查循环结构的程序框图,由框图运行程序我们可知.
第①步,运行i=1,S=0+lg=lg>-1
第②步,i=3,S=lg+lg=lg>-1
第③步,
i=5,S=lg+lg=lg>-1
第④步,i=7,S=lg+lg=lg>-1
第⑤步,i=9,S=lg+lg=lg<-1
程序框图结束此时输出i=9,故选B,本题解题关键①是找到对数的运算规律,②要掌握好每执行一步程序,i与S的函代关系.
2.执行下面的程序框图,如果输入a=4,那么输出的n的值为( )
A.2
B.3
C.4
D.5
[答案] B
[解析] 本题考查了算法循环结构的直到型的流程图问题.n=0,p=0+40=1,q=2+1=3;
n=1,p=1+41=5,q=6+1=7;
n=2,p=5+42=21,q=14+1=15,n=3,p>q.
算法的考查多以流程图的形式出现,重点考查的是循环结构.
二、填空题
3.阅读如下图所示的算法框图,若输入m=4,n=3,则输出a=________,i=________.
[答案] 6 2
[解析] 该算法框图的执行过程是:
m=4
n=3
i=1
a=4+1=5
3整除5 否
i=1+1=2
a=4+2=6
3整除6 是
输出a=6,i=2.
4.(2015·山东文,11)执行下边的程序框图,若输入的x的值为1,则输出的y的值是________.
[答案] 13
[解析] 第一次执行程序,满足条件x<2,x=1+1=2;第二次执行程序,不满足条件x<2,y=3×22+1=13,输出y=13,结束.答案为13.
三、解答题
5.画出求(共6个2)的值的算法的流程图.
[分析] 这个式子实际上是求和,取倒数;再求和,取倒数;反复五次即达到目的.第一个和为2+.
[解析] 流程图如下图所示.
6.用N1代表第一个学生的学号,Ni代表第i个学生的学号,Gi代表第i个学生的成绩,那么如图,表示一个什么样的算法?
[解析] 算法:
第一步:i=1;
第二步:如果Gi≥90,则输出Ni,Gi,否则直接转到第三步;
第三步:i=i+1;
第四步:如果i≤60,则执行第二步,重复执行第二步、第三步、第四步,否则结束.
故该框图表示的算法功能是:输出60名学生中分数在90分或90分以上的学生的学号和成绩.
7.设计一个计算20个数的平均数的算法,并画出相应的流程图.
[解析] 算法如下.
1 S=0.
2 i=1.
3 输入G.
4 S=S+G.
5 i=i+1.
6 如果i不大于20,转3;如果i大于20,退出循环.
7 A=.
8 输出A.
流程图如下图所示.
