2.2.3 循环结构 同步测试(含答案)
文档属性
| 名称 | 2.2.3 循环结构 同步测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 528.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-17 00:00:00 | ||
图片预览


文档简介
2.2.3循环结构
同步测试
一、选择题(每小题3分,共18分)
1.(2014·吉安高一检测)阅读如图所示的算法框图,输出的i值等于 ( )
A.2 B.3 C.4 D.5
【解析】选C.①s=0,i=1;②a=1×21,s=0+1×21,i=2;
③a=2×22=8,s=2+8=10,i=3;④a=3×23=24,s=34,i=4.
此时结束循环,输出i=4.
【举一反三】若把判断框内“s>11”改为“s>20142”,则此算法框图中表示的关于s的一个不等式是________.
【解析】由题意知s=1×21+2×22+3×23+…+i×2i>20142.
答案:1×21+2×22+3×23+…+i×2i>20142
2.(2014·泰安高一检测)执行如图的算法框图,如果输入的N是6,那么输出的p是 ( )
A.120
B.720
C.1080
D.5040
【解析】选B.①k=1,p=1;②k=2,p=1×2=2;③k=3,p=2×3=6;④k=4,p=6×4=24;⑤k=5,p=24×5=120;
⑥k=6,p=120×6=720.
【变式训练】执行如图所示的算法框图,若输入n的值为6,则输出s的值为
( )
A.105
B.16
C.15
D.1
【解析】选C.①i=1,s=1;②s=1×1=1,i=3;③s=1×3=3,i=5;④s=3×5=15,i=7,此时输出s=15.
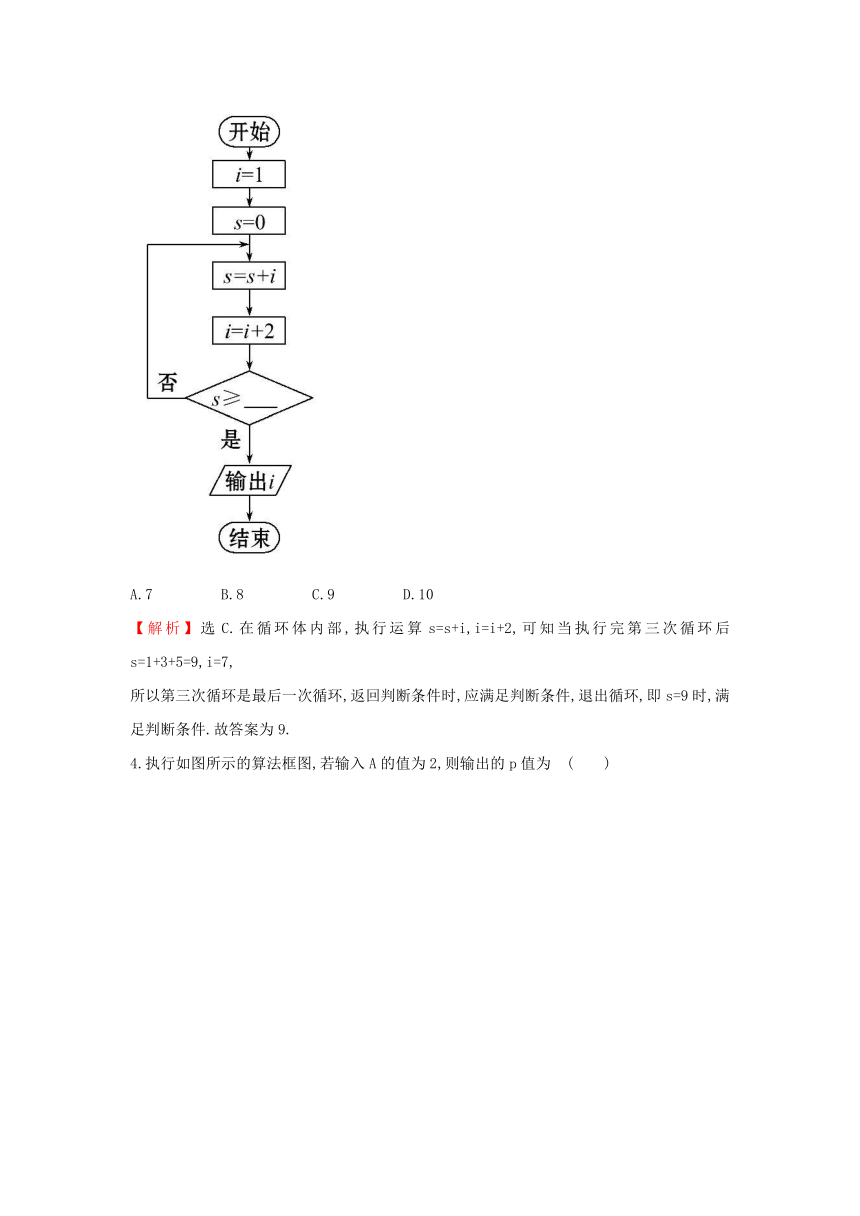
3.运行如图所示的算法框图,若输出的结果是7,则判断框中的横线上可以填入的最大整数为 ( )
A.7
B.8
C.9
D.10
【解析】选C.在循环体内部,执行运算s=s+i,i=i+2,可知当执行完第三次循环后s=1+3+5=9,i=7,
所以第三次循环是最后一次循环,返回判断条件时,应满足判断条件,退出循环,即s=9时,满足判断条件.故答案为9.
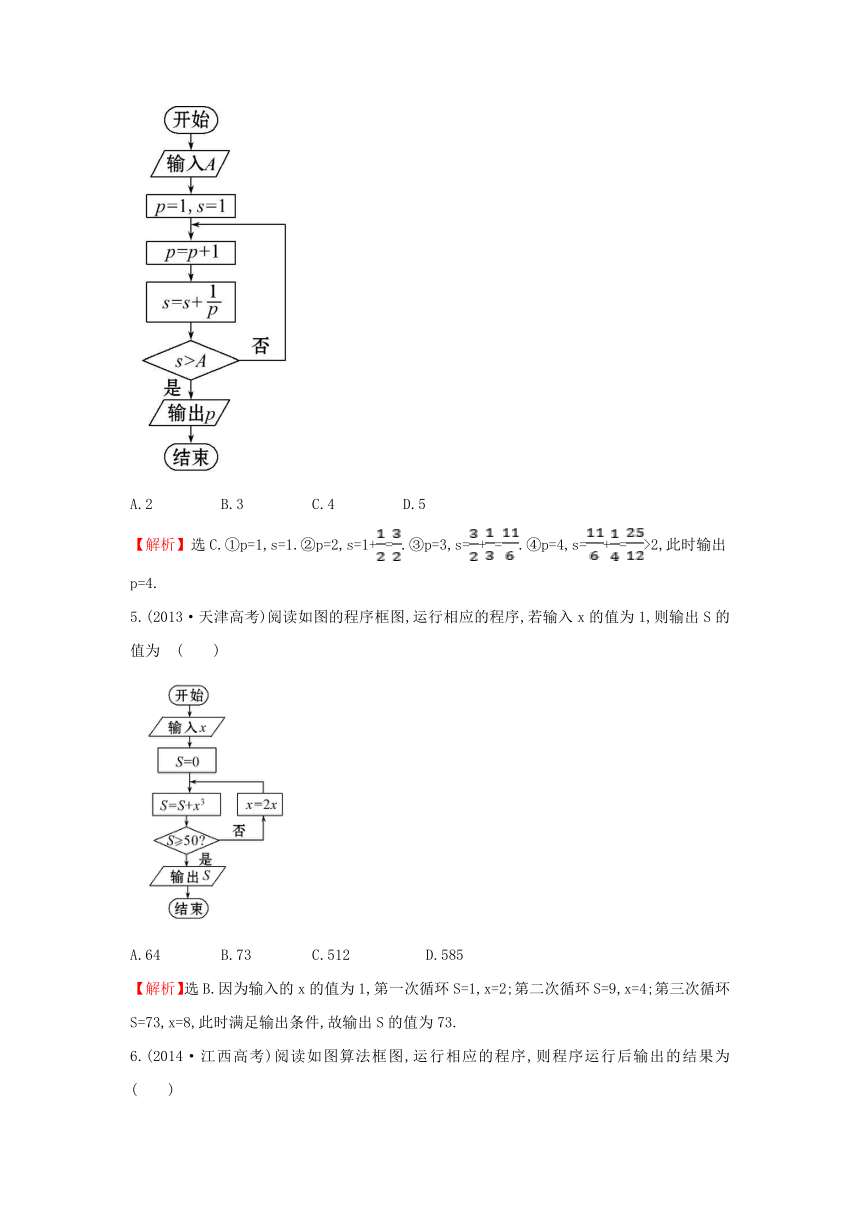
4.执行如图所示的算法框图,若输入A的值为2,则输出的p值为 ( )
A.2
B.3
C.4
D.5
【解析】选C.①p=1,s=1.②p=2,s=1+=.③p=3,s=+=.④p=4,s=+=>2,此时输出p=4.
5.(2013·天津高考)阅读如图的程序框图,运行相应的程序,若输入x的值为1,则输出S的值为 ( )
A.64 B.73 C.512 D.585
【解析】选B.因为输入的x的值为1,第一次循环S=1,x=2;第二次循环S=9,x=4;第三次循环S=73,x=8,此时满足输出条件,故输出S的值为73.
6.(2014·江西高考)阅读如图算法框图,运行相应的程序,则程序运行后输出的结果为 ( )
A.7
B.9
C.10
D.11
【解题指南】把每次执行循环体后S及i的值计算出来,直到满足条件为止.
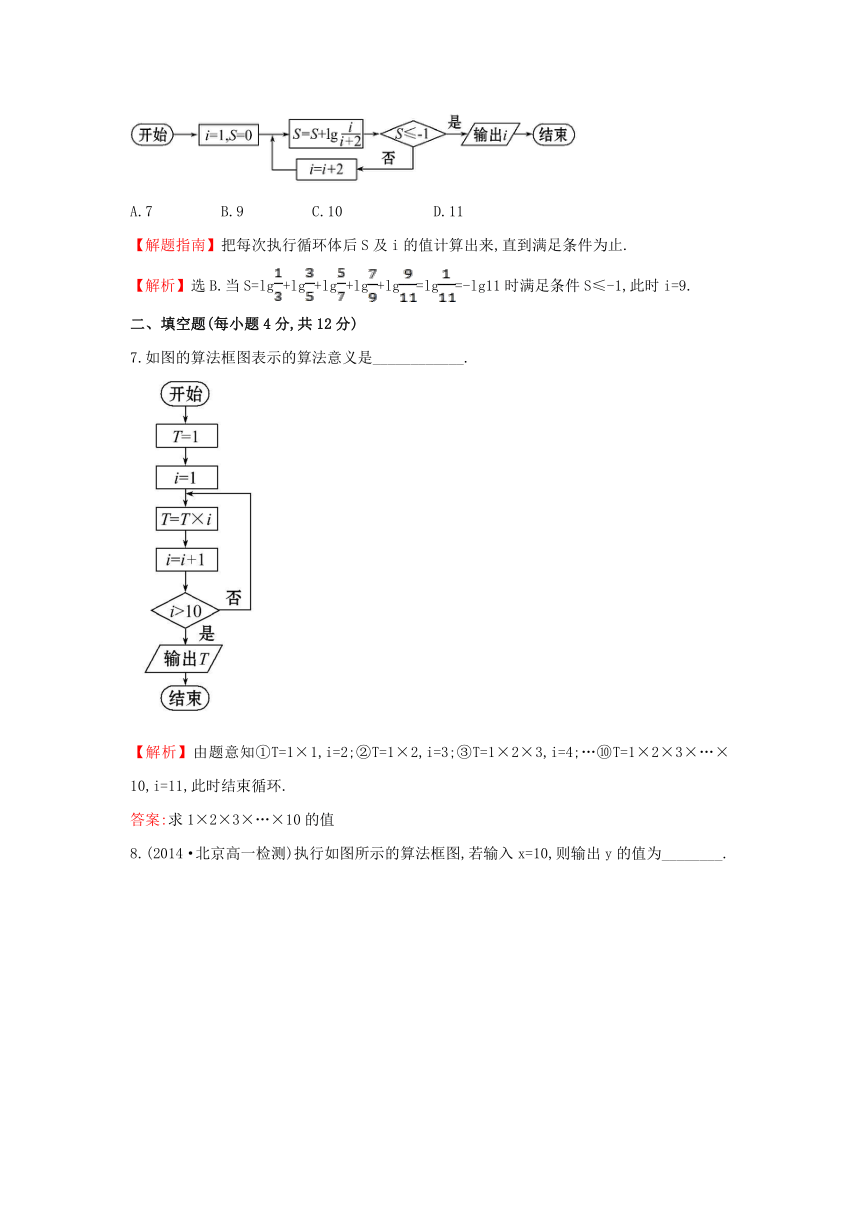
【解析】选B.当S=lg+lg+lg+lg+lg=lg=-lg11时满足条件S≤-1,此时i=9.
二、填空题(每小题4分,共12分)
7.如图的算法框图表示的算法意义是____________.
【解析】由题意知①T=1×1,i=2;②T=1×2,i=3;③T=1×2×3,i=4;…⑩T=1×2×3×…×10,i=11,此时结束循环.
答案:求1×2×3×…×10的值
8.(2014·北京高一检测)执行如图所示的算法框图,若输入x=10,则输出y的值为________.
【解析】①x=10,y=4;②x=4,y=1;③x=1,y=-;④x=-,y=-,退出循环,输出y.
答案:-
9.执行如图所示的算法框图,输出的S值为__________.
【解析】i=0,S=1;S==,i=1;S==×=,i=2,此时满足输出条件,输出S的值为.
答案:
三、解答题(每小题10分,共20分)
10.求当x=-8,-7.2,-6.4,…,-4时,函数y=2x2+3对应的函数值,试画出解决该问题的算法框图.
【解析】算法框图如图:
11.画出求使1+2+3…+n>10000成立的最小自然数n的算法框图.
【解析】
【举一反三】画算法框图,求使1×3×5×7×…×n>50000成立的最小正整数n.
【解析】算法框图如图:
一、选择题(每小题4分,共16分)
1.(2014·菏泽高一检测)如图所示的框图的功能是计算表达式++…+的值,则在①②两处应填 ( )
A.n=0和n>10
B.n=0和n≥10
C.n=1和n>10
D.n=1和n≥10
【解题指南】给出算法功能,要求补全框图中的条件时,首先要明确控制变量,其次要分析循环终止的条件,最后再看是否满足条件跳出循环,从而确定条件.
【解析】选B.算法框图中,S是累加变量,n是计数变量.由于在累加S=S+之前是n=n+1,所以n的初始值应为0.又因为S=++…+,所以循环终止条件是n=10,故判断框内应填n≥10.
2.某算法框图如图所示,若输出S=57,则判断框内为 ( )
A.k>4
B.
k>5
C.k>6
D.k>7
【解析】选A.①S=1,k=1;②k=2,S=2×1+2=4;③k=3,S=2×4+3=11;④k=4,S=2×11+4=26;⑤k=5,S=2×26+5=57.
此时,k应满足判断框内的条件,输出S.
【变式训练】按如图所示的算法框图运行时,输出的结果是63,那么判断框内整数M的值为________.
【解析】S=2×1+1=3,A变为2;
A=2>M,“否”,则S=2×3+1=7,A变为3;
A=3>M,“否”,则S=2×7+1=15,A变为4;
A=4>M,“否”,则S=2×15+1=31,A变为5;
A=5>M,“否”,则S=2×31+1=63,A变为6;
A=6>M,“是”,则跳出循环,故M的值为5.
答案:5
3.下列四个程序框图都是为计算22+42+62+…+1002而设计的,其中正确的是
( )
【解题指南】根据题目的要求逐一验证.
【解析】选D.执行A,得p=22+42+(42+1)+(42+2)+…+(42+84),与题意不符;
执行B,得p=22+42+42+42+…,不能执行到底,与题意不符;
执行C,得p=22+42+62+…+982,与题意不符;
执行D,得p=0+22+42+62+…+1002,满足题意.
4.(2013·江西高考)阅读如图程序框图,如果输出i=5,那么在空白矩形框中应填入的语句为 ( )
A.s=2i-2
B.s=2i-1
C.s=2i
D.s=2i+4
【解析】选C.由题意知矩形框中的语句必须满足两个条件,i=5时s≥10,且i=3时s<10,经验证只有选项C适合.
二、填空题(每小题5分,共10分)
5.(2013·温州高一检测)若如图所示的算法框图运行结果为S=90,那么判断框中应填入的关于k的条件是________.
【解析】k=10时,S=1×10=10;
k=9时,S=10×9=90.
又因为运行结果为S=90,
所以k=8时应输出S.
所以判断框中应填入k≤8.
答案:k≤8
【误区警示】解答本题易误填k≤9,出错的原因是识图不清,弄错循环次数.
【变式训练】如图是求的值的算法框图,则图中判断框中应填入条件________.
【解题指南】本题结构复杂,只要找出题目中含有多少个即可.
【解析】i=1时,得到A=,共需执行此循环5次,故填i>5.
答案:i>5
6.(2014·济宁模拟)执行如图的算法框图,若P=0.95,则输出的n=________.
【解析】①S=0,n=1;②S=0+=,n=2;③S=+=0.75,n=3;④S=0.75+=0.875,n=4;⑤S=0.875+0.0625=0.9375,n=5;⑥S=0.9375+=0.96875,n=6.此时结束循环,所以n=6.
答案:6
【方法技巧】利用循环结构表示算法的关注点
(1)要选择准确的表示累计的变量.
(2)要注意在哪一步结束循环.
(3)执行完整每一次循环,防止执行程序不彻底,造成错误.
三、解答题(每小题12分,共24分)
7.(2013·广州高一检测)某中学高三年级男子体育训练小组5月测试的50米跑的成绩(单位:s)如下:6.4,6.5,7.0,
6.8,7.1,7.3,6.9,7.4,7.5,设计一个算法,从这些成绩中搜索出小于6.8s的成绩,并画出程序框图.
【解析】算法步骤如下:
第一步,i=1;
第二步,输入一个数据a;
第三步,如果a<6.8,则输出a,否则,执行第四步;
第四步,i=i+1;
第五步,如果i>9,则结束算法.否则执行第二步.
程序框图如图所示:
8.运行如图所示的算法框图.
(1)若输入x的值为2,根据运行过程完成下面的表格,并求输出的i与x的值.
第i次
i=1
i=2
i=3
i=4
i=5
x=2×3i
(2)若输出i的值为2,求输入x的取值范围.
【解析】(1)
第i次
i=1
i=2
i=3
i=4
i=5
x=2×3i
6
18
54
162
486
因为162<168,486>168,所以输出的i的值为5,x的值为486.
(2)由输出i的值为2,则程序执行了循环体2次,
即
解得所以输入x的取值范围是
同步测试
一、选择题(每小题3分,共18分)
1.(2014·吉安高一检测)阅读如图所示的算法框图,输出的i值等于 ( )
A.2 B.3 C.4 D.5
【解析】选C.①s=0,i=1;②a=1×21,s=0+1×21,i=2;
③a=2×22=8,s=2+8=10,i=3;④a=3×23=24,s=34,i=4.
此时结束循环,输出i=4.
【举一反三】若把判断框内“s>11”改为“s>20142”,则此算法框图中表示的关于s的一个不等式是________.
【解析】由题意知s=1×21+2×22+3×23+…+i×2i>20142.
答案:1×21+2×22+3×23+…+i×2i>20142
2.(2014·泰安高一检测)执行如图的算法框图,如果输入的N是6,那么输出的p是 ( )
A.120
B.720
C.1080
D.5040
【解析】选B.①k=1,p=1;②k=2,p=1×2=2;③k=3,p=2×3=6;④k=4,p=6×4=24;⑤k=5,p=24×5=120;
⑥k=6,p=120×6=720.
【变式训练】执行如图所示的算法框图,若输入n的值为6,则输出s的值为
( )
A.105
B.16
C.15
D.1
【解析】选C.①i=1,s=1;②s=1×1=1,i=3;③s=1×3=3,i=5;④s=3×5=15,i=7,此时输出s=15.
3.运行如图所示的算法框图,若输出的结果是7,则判断框中的横线上可以填入的最大整数为 ( )
A.7
B.8
C.9
D.10
【解析】选C.在循环体内部,执行运算s=s+i,i=i+2,可知当执行完第三次循环后s=1+3+5=9,i=7,
所以第三次循环是最后一次循环,返回判断条件时,应满足判断条件,退出循环,即s=9时,满足判断条件.故答案为9.
4.执行如图所示的算法框图,若输入A的值为2,则输出的p值为 ( )
A.2
B.3
C.4
D.5
【解析】选C.①p=1,s=1.②p=2,s=1+=.③p=3,s=+=.④p=4,s=+=>2,此时输出p=4.
5.(2013·天津高考)阅读如图的程序框图,运行相应的程序,若输入x的值为1,则输出S的值为 ( )
A.64 B.73 C.512 D.585
【解析】选B.因为输入的x的值为1,第一次循环S=1,x=2;第二次循环S=9,x=4;第三次循环S=73,x=8,此时满足输出条件,故输出S的值为73.
6.(2014·江西高考)阅读如图算法框图,运行相应的程序,则程序运行后输出的结果为 ( )
A.7
B.9
C.10
D.11
【解题指南】把每次执行循环体后S及i的值计算出来,直到满足条件为止.
【解析】选B.当S=lg+lg+lg+lg+lg=lg=-lg11时满足条件S≤-1,此时i=9.
二、填空题(每小题4分,共12分)
7.如图的算法框图表示的算法意义是____________.
【解析】由题意知①T=1×1,i=2;②T=1×2,i=3;③T=1×2×3,i=4;…⑩T=1×2×3×…×10,i=11,此时结束循环.
答案:求1×2×3×…×10的值
8.(2014·北京高一检测)执行如图所示的算法框图,若输入x=10,则输出y的值为________.
【解析】①x=10,y=4;②x=4,y=1;③x=1,y=-;④x=-,y=-,退出循环,输出y.
答案:-
9.执行如图所示的算法框图,输出的S值为__________.
【解析】i=0,S=1;S==,i=1;S==×=,i=2,此时满足输出条件,输出S的值为.
答案:
三、解答题(每小题10分,共20分)
10.求当x=-8,-7.2,-6.4,…,-4时,函数y=2x2+3对应的函数值,试画出解决该问题的算法框图.
【解析】算法框图如图:
11.画出求使1+2+3…+n>10000成立的最小自然数n的算法框图.
【解析】
【举一反三】画算法框图,求使1×3×5×7×…×n>50000成立的最小正整数n.
【解析】算法框图如图:
一、选择题(每小题4分,共16分)
1.(2014·菏泽高一检测)如图所示的框图的功能是计算表达式++…+的值,则在①②两处应填 ( )
A.n=0和n>10
B.n=0和n≥10
C.n=1和n>10
D.n=1和n≥10
【解题指南】给出算法功能,要求补全框图中的条件时,首先要明确控制变量,其次要分析循环终止的条件,最后再看是否满足条件跳出循环,从而确定条件.
【解析】选B.算法框图中,S是累加变量,n是计数变量.由于在累加S=S+之前是n=n+1,所以n的初始值应为0.又因为S=++…+,所以循环终止条件是n=10,故判断框内应填n≥10.
2.某算法框图如图所示,若输出S=57,则判断框内为 ( )
A.k>4
B.
k>5
C.k>6
D.k>7
【解析】选A.①S=1,k=1;②k=2,S=2×1+2=4;③k=3,S=2×4+3=11;④k=4,S=2×11+4=26;⑤k=5,S=2×26+5=57.
此时,k应满足判断框内的条件,输出S.
【变式训练】按如图所示的算法框图运行时,输出的结果是63,那么判断框内整数M的值为________.
【解析】S=2×1+1=3,A变为2;
A=2>M,“否”,则S=2×3+1=7,A变为3;
A=3>M,“否”,则S=2×7+1=15,A变为4;
A=4>M,“否”,则S=2×15+1=31,A变为5;
A=5>M,“否”,则S=2×31+1=63,A变为6;
A=6>M,“是”,则跳出循环,故M的值为5.
答案:5
3.下列四个程序框图都是为计算22+42+62+…+1002而设计的,其中正确的是
( )
【解题指南】根据题目的要求逐一验证.
【解析】选D.执行A,得p=22+42+(42+1)+(42+2)+…+(42+84),与题意不符;
执行B,得p=22+42+42+42+…,不能执行到底,与题意不符;
执行C,得p=22+42+62+…+982,与题意不符;
执行D,得p=0+22+42+62+…+1002,满足题意.
4.(2013·江西高考)阅读如图程序框图,如果输出i=5,那么在空白矩形框中应填入的语句为 ( )
A.s=2i-2
B.s=2i-1
C.s=2i
D.s=2i+4
【解析】选C.由题意知矩形框中的语句必须满足两个条件,i=5时s≥10,且i=3时s<10,经验证只有选项C适合.
二、填空题(每小题5分,共10分)
5.(2013·温州高一检测)若如图所示的算法框图运行结果为S=90,那么判断框中应填入的关于k的条件是________.
【解析】k=10时,S=1×10=10;
k=9时,S=10×9=90.
又因为运行结果为S=90,
所以k=8时应输出S.
所以判断框中应填入k≤8.
答案:k≤8
【误区警示】解答本题易误填k≤9,出错的原因是识图不清,弄错循环次数.
【变式训练】如图是求的值的算法框图,则图中判断框中应填入条件________.
【解题指南】本题结构复杂,只要找出题目中含有多少个即可.
【解析】i=1时,得到A=,共需执行此循环5次,故填i>5.
答案:i>5
6.(2014·济宁模拟)执行如图的算法框图,若P=0.95,则输出的n=________.
【解析】①S=0,n=1;②S=0+=,n=2;③S=+=0.75,n=3;④S=0.75+=0.875,n=4;⑤S=0.875+0.0625=0.9375,n=5;⑥S=0.9375+=0.96875,n=6.此时结束循环,所以n=6.
答案:6
【方法技巧】利用循环结构表示算法的关注点
(1)要选择准确的表示累计的变量.
(2)要注意在哪一步结束循环.
(3)执行完整每一次循环,防止执行程序不彻底,造成错误.
三、解答题(每小题12分,共24分)
7.(2013·广州高一检测)某中学高三年级男子体育训练小组5月测试的50米跑的成绩(单位:s)如下:6.4,6.5,7.0,
6.8,7.1,7.3,6.9,7.4,7.5,设计一个算法,从这些成绩中搜索出小于6.8s的成绩,并画出程序框图.
【解析】算法步骤如下:
第一步,i=1;
第二步,输入一个数据a;
第三步,如果a<6.8,则输出a,否则,执行第四步;
第四步,i=i+1;
第五步,如果i>9,则结束算法.否则执行第二步.
程序框图如图所示:
8.运行如图所示的算法框图.
(1)若输入x的值为2,根据运行过程完成下面的表格,并求输出的i与x的值.
第i次
i=1
i=2
i=3
i=4
i=5
x=2×3i
(2)若输出i的值为2,求输入x的取值范围.
【解析】(1)
第i次
i=1
i=2
i=3
i=4
i=5
x=2×3i
6
18
54
162
486
因为162<168,486>168,所以输出的i的值为5,x的值为486.
(2)由输出i的值为2,则程序执行了循环体2次,
即
解得
