2.2.3 循环结构 学案2(含答案)
图片预览




文档简介
2.2.3 循环结构
学案
课标解读
1.了解循环结构的概念,掌握循环结构的特点及功能(重点).2.能运用算法框图表示循环结构,并通过模仿、操作、探索设计循环结构解决问题(难点).
知识1
循环结构的概念
【问题导思】
伦敦举办了2012年第30届夏季奥运会,你知道在申办奥运会的最后阶段,国际奥委会是如何通过投票决定主办权归属吗?对竞选出的5个申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票超过总票数的一半,那么该城市就获得主办权;如果所有申办城市得票数都不超过总票数的一半,则将得票最少的城市淘汰,然后重复上述过程,直到选出一个申办城市为止.
1.上述投票选举城市申办奥运会是算法吗?
【提示】 是.
2.该算法若用框图表示,只有顺序结构与选择结构可以吗?
【提示】 不可以.
3.在该算法中,要多次重复操作,那么控制重复操作的条件及重复的内容是什么?
【提示】 控制重复操作的条件为是否有城市得票超过总票数的一半,重复的内容是淘汰得票最少的城市.
1.定义
按照一定条件,反复执行某一步骤的算法结构称为循环结构,反复执行的部分称为循环体.
2.循环变量
控制着循环的开始和结束的变量,称为循环变量.
3.循环的终止条件
决定是否继续执行循环体的判断条件,称为循环的终止条件.
知识2
循环结构的基本模式
在画出循环结构的算法框图之前,需要确定三件事:
1.确定循环变量和初始条件;
2.确定算法中反复执行的部分,即循环体;
3.确定循环的终止条件.
这样,循环结构的算法框图的基本模式如图所示:
图2-2-10
类型1
利用循环结构解决累加(乘)问题
设计一个算法,求1+2+22+…+249的值,并画出算法框图.
【思路探究】 解答本题可由累加问题入手,计数变量顺次加1,然后确定循环变量及初始条件,再依据算法步骤画出框图.
【自主解答】 算法如下:
(1)S=0;
(2)i=0;
(3)S=S+2i;
(4)i=i+1;
(5)如果i不大于49,返回重新执行(3)、(4),否则执行(6);
(6)输出S的值.
算法框图如图:
1.本题中由于加数众多,不宜采用逐一相加的思路,进行这种运算都是通过循环结构实现的,方法是引进两个变量i和S.其中i一般称为计数变量,用来计算和控制运算次数,S称为累积变量,它表示所求得的和或积,它是不断地将前一个结果与新数相加或相乘得到的.这两个变量的表示形式一般为i=i+m(m为每次增加的数值)和S=S+A(A为所加的数)或S=S
A(A为所乘的数).
2.如果算法问题中涉及到的运算进行了多次重复,且参与运算的数前后有规律可循,就可以引入变量以参与循环结构.
3.在不同的循环结构中,应注意判断条件的差别及计数变量和累加(乘)变量的初值与运算框先后关系的对应性.
(2013·成都高一检测)设计求1×2×3×4×…×2
012的算法.
【解】 算法如下:
1.设m的值为1;
2.设i的值为2;
3.如果i≤2
012,则执行第四步,否则转去执行第六步;
4.计算m乘i并将结果赋给m;
5.计算i加1并将结果赋给i,转去执行第三步;
6.输出m的值并结束算法.
算法框图,如图所示:
类型2
代数运算问题的算法设计
画出求
的值的算法框图.
【思路探究】 (1)找循环变量i每次递增1,故只需式子i=i+1.
(2)设置循环体,观察这个数的特点是从里向外根号依次增多还多乘一个2,可以设置为A=.
(3)设置循环的终止条件i>5.
【自主解答】
1.这类比较特殊的数要注意找规律,本题的规律是对2开方,然后乘2再开方重复进行直到满足要求为止.
2.设计的关键是循环体的设置及循环的终止条件.
画出求(共6个2)的值的算法框图.
【解】 算法框图如下:
类型3
利用循环结构解决筛选问题
给出以下10个数:5,9,80,43,95,73,28,17,60,36,要求把大于40的数找出来并输出,试画出解决该问题的算法框图.
【思路探究】 可以考虑从第1个数开始与40比较大小,共需比较10次,可以设计一个计数变量来控制比较的次数.利用循环结构来设计算法.
【自主解答】
1.本题的算法设计中用了选择结构及循环结构.选择结构用于判断输入的数是否大于40,循环结构用于控制输入的数的个数.
2.在设计算法时,循环结构和选择结构可以综合应用.
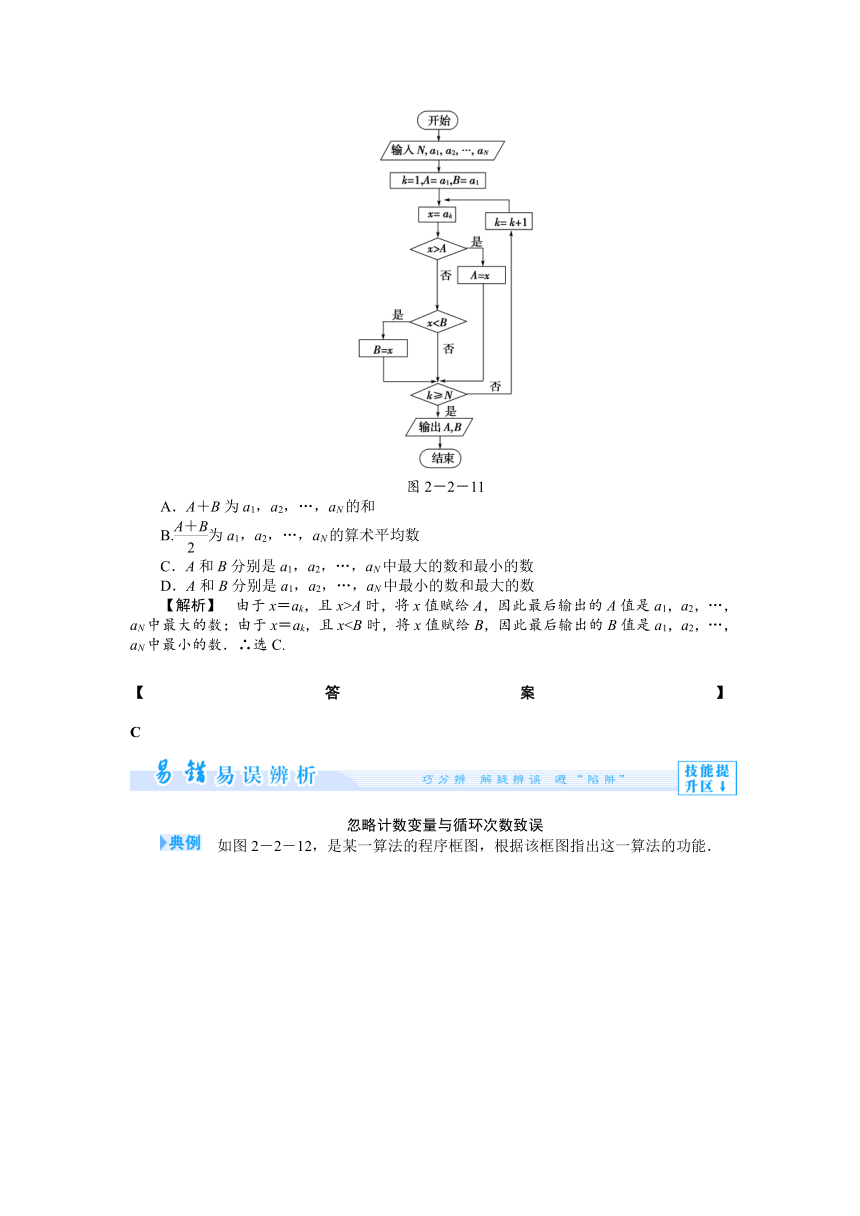
(2012·课标全国卷)如果执行如图2-2-11所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )
图2-2-11
A.A+B为a1,a2,…,aN的和
B.为a1,a2,…,aN的算术平均数
C.A和B分别是a1,a2,…,aN中最大的数和最小的数
D.A和B分别是a1,a2,…,aN中最小的数和最大的数
【解析】 由于x=ak,且x>A时,将x值赋给A,因此最后输出的A值是a1,a2,…,aN中最大的数;由于x=ak,且x【答案】 C
忽略计数变量与循环次数致误
如图2-2-12,是某一算法的程序框图,根据该框图指出这一算法的功能.
图2-2-12
【错解】 求S=++++的值.
【错因分析】 本题忽略了计数变量与循环次数,没有明确循环体在循环结构中的作用,以及循环终止条件决定是否继续执行循环体.
【防范措施】 在循环过程中要明确循环的次数,明确起始数据和其后面数据的变化规律.
【正解】 在该程序框图中,S与n为两个累加变量,k为计数变量,所以该算法的功能是求+++…+的值.
1.设计一个算法框图算法的一般步骤
(1)用自然语言表述算法步骤;
(2)确定每一个算法步骤所包含的逻辑结构,并用相应的算法框图表示,得到表示该步骤的算法框图;
(3)将所有步骤的算法框图用流程线连接起来,并加上终端框,得到表示整个算法的算法框图.
2.循环结构的关键是要理解“累加变量”和“计数变量”,累加变量常用S表示,计数变量常用i表示.每循环一次,S和i都发生变化,根据判断框内的循环条件,直到中止循环为止.
1.如图2-2-13所示算法框图中的循环体是( )
图2-2-13
A.A B.C
C.ABCD
D.BD
【解析】 循环体是反复执行的部分,是BD,
故选D.
【答案】 D
2.(2013·天津高考)阅读如图2-2-14所示的程序框图,运行相应的程序.若输入x的值为1,则输出S的值为( )
图2-2-14
A.64 B.73 C.512 D.585
【解析】 程序框图执行过程如下:x=1,S=0,S=1,S<50 x=2,S=9,S<50 x=4,S=73>50,跳出循环,输出S=73.
【答案】 B
3.(2013·广东高考)执行如图2-2-15所示的程序框图,若输入n的值为4,则输出s的值为________.
图2-2-15
【解析】 第一步运算结果:s=1,i=2(i≤4成立);第二步运算结果:s=2,i=3(i≤4成立);第三步运算结果:s=4,i=4(i≤4成立);第四步运算结果:s=7,i=5(i≤4不成立),程序结束,故输出s的值为7.
【答案】 7
4.求1+2+3+4+…+110的值,写出算法步骤画出算法框图.
【解】 算法步骤:
(1)i=1,sum=0;
(2)sum=sum+i;
(3)i=i+1;
(4)如果i≤110,则执行第二步,否则执行下一步;
(5)输出sum.
算法框图如图所示:
一、选择题
1.(2013·重庆高考)执行如图2-2-16所示的程序框图,则输出的k的值是( )
图2-2-16
A.3 B.4 C.5 D.6
【解析】 k=1,s=1+02=1;k=2,s=1+12=2;k=3,s=2+22=6;k=4,s=6+32=15,k=5,s=15+42=31>15.故输出k=5,选C.
【答案】 C
2.(2013·辽宁高考)执行如图2-2-17所示的程序框图,若输入n=10,则输出S=( )
图2-2-17
A.
B.
C.
D.
【解析】 因为S=,i=4<10,所以S=+=,i=6<10,所以S=+=,i=8<10,所以S=+=,i=10=10,所以S=+=,i=12>10,输出S=.
【答案】 A
3.如图2-2-18所示框图表示的算法的功能是( )
图2-2-18
A.计算小于100的奇数的连乘积
B.计算从1开始的连续奇数的连乘积
C.从1开始的连续奇数的连乘积,当乘积大于100时,计算奇数的个数
D.计算1×3×5×7×…×n≥100时的最小的n值
【解析】 由框图知s=1×3×5×…×n.又因为循环结束的条件是s≥100,故其算法功能为:计算1×3×5×…×n≥100时的最小的n值.
【答案】 D
4.(2013·山东高考)执行两次如图2-2-19所示的程序框图,若第一次输入的a的值为-1.2,第二次输入的a的值为1.2,则第一次,第二次输出的a的值分别为( )
图2-2-19
A.0.2,0.2
B.0.2,0.8
C.0.8,0.2
D.0.8,0.8
【解析】 由程序框图可知:当a=-1.2时,∵a<0,
∴a=-1.2+1=-0.2,a<0,
a=-0.2+1=0.8,a>0.
∵0.8<1,输出a=0.8.
当a=1.2时,∵a≥1,
∴a=1.2-1=0.2.
∵0.2<1,输出a=0.2.
【答案】 C
图2-2-20
5.某算法框图如图2-2-20所示,若输出的S=57,则判断框内为( )
A.k>4 B.k>5
C.k>6
D.k>7
【解析】 k=1时,k=k+1=2,
S=2S+k=2×1+2=4;
k=2时,k=k+1=2+1=3,
S=2S+k=2×4+3=11;
k=3时,k=k+1=4,S=2S+k=2×11+4=26;
k=4时,k=k+1=5,S=2S+k=2×26+5=57.
此时S=57,循环结束,k=5,所以判断框内应填“k>4”,故选A.
【答案】 A
二、填空题(每小题5分,共10分)
6.(2013·江苏高考)如图是一个算法的流程图,则输出的n的值是________.
图2-2-21
【解析】 算法流程图执行过程如下:
n=1,a=2,a<20;
a=8,n=2,a<20;
a=26,n=3,a>20.
输出n=3.
【答案】 3
7.如图2-2-22所示的算法框图的功能是计算2×4×6×…×100的值,则处理框内应填________.
图2-2-22
【解析】 参与求积的因数皆为正偶数,故i的变化应保持始终是偶数,故i=i+2.
【答案】 i=i+2
8.如图2-2-23是统计该6名队员在最近三场比赛中投进的三分球总数的算法框图,则图中判断框应填________,输出的s=________.
图2-2-23
【解析】 观察算法框图可以看出,判断框内的条件满足时才执行循环体,所以判断框应填i≤6,输出的s是这6名队员成绩的和,即s=a1+a2+a3+a4+a5+a6.
【答案】 i≤6 a1+a2+a3+a4+a5+a6
三、解答题
9.计算下面的和:+++…+,画出其算法框图.
【解】 算法框图如图所示:
10.某高中男子体育小组的50
m赛跑成绩(单位:s)为6.4,6.5,7.0,6.8,7.1,7.3,6.9,7.4,7.5,7.6,6.3,6.4,6.4,6.5,6.7,7.1,6.9,6.4,7.1,7.0.设计一个算法,从这些成绩中搜索出小于6.8
s的成绩,并画出流程图.
【解】 体育小组共20人,要解决该问题必须对运动员进行编号,设第i个运动员编号为Ni,成绩为Gi.可以设计下面的算法.
算法如下:
第一步,i=1;
第二步,输入Ni,Gi;
第三步,如果Gi<6.8,则输出Ni、Gi,并执行第四步,否则,也执行第四步;
第四步,i=i+1;
第五步,如果i>20,则结束,否则返回第二步.
算法框图如图所示:
11.阅读如图2-2-24所示的算法框图,若输入n0=0,
则输出的结果为多少?
图2-2-24
【解】 当n0=0时,n=0,
n=n+1=0+1=1,
m==20∈N,且20≠1,所以输出m=20;
n=1+1=2,m==10,且10≠1,输出10;
n=2+1=3,m= N,
n=3+1=4,
m==5∈N,且5≠1,∴输出m=5;
n=4+1=5,m==4∈N,且4≠1,∴输出m=4;
n=6,7,8时均不输出,n=9时,n+1=10,m=2∈N,且2≠1,输出m=2.
n=11,12,13,14,15,16,17,18时均不输出,
n=19时,n+1=20,m=1∈N,结束.
∴综上,输出的结果为20,10,5,4,2.
学案
课标解读
1.了解循环结构的概念,掌握循环结构的特点及功能(重点).2.能运用算法框图表示循环结构,并通过模仿、操作、探索设计循环结构解决问题(难点).
知识1
循环结构的概念
【问题导思】
伦敦举办了2012年第30届夏季奥运会,你知道在申办奥运会的最后阶段,国际奥委会是如何通过投票决定主办权归属吗?对竞选出的5个申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票超过总票数的一半,那么该城市就获得主办权;如果所有申办城市得票数都不超过总票数的一半,则将得票最少的城市淘汰,然后重复上述过程,直到选出一个申办城市为止.
1.上述投票选举城市申办奥运会是算法吗?
【提示】 是.
2.该算法若用框图表示,只有顺序结构与选择结构可以吗?
【提示】 不可以.
3.在该算法中,要多次重复操作,那么控制重复操作的条件及重复的内容是什么?
【提示】 控制重复操作的条件为是否有城市得票超过总票数的一半,重复的内容是淘汰得票最少的城市.
1.定义
按照一定条件,反复执行某一步骤的算法结构称为循环结构,反复执行的部分称为循环体.
2.循环变量
控制着循环的开始和结束的变量,称为循环变量.
3.循环的终止条件
决定是否继续执行循环体的判断条件,称为循环的终止条件.
知识2
循环结构的基本模式
在画出循环结构的算法框图之前,需要确定三件事:
1.确定循环变量和初始条件;
2.确定算法中反复执行的部分,即循环体;
3.确定循环的终止条件.
这样,循环结构的算法框图的基本模式如图所示:
图2-2-10
类型1
利用循环结构解决累加(乘)问题
设计一个算法,求1+2+22+…+249的值,并画出算法框图.
【思路探究】 解答本题可由累加问题入手,计数变量顺次加1,然后确定循环变量及初始条件,再依据算法步骤画出框图.
【自主解答】 算法如下:
(1)S=0;
(2)i=0;
(3)S=S+2i;
(4)i=i+1;
(5)如果i不大于49,返回重新执行(3)、(4),否则执行(6);
(6)输出S的值.
算法框图如图:
1.本题中由于加数众多,不宜采用逐一相加的思路,进行这种运算都是通过循环结构实现的,方法是引进两个变量i和S.其中i一般称为计数变量,用来计算和控制运算次数,S称为累积变量,它表示所求得的和或积,它是不断地将前一个结果与新数相加或相乘得到的.这两个变量的表示形式一般为i=i+m(m为每次增加的数值)和S=S+A(A为所加的数)或S=S
A(A为所乘的数).
2.如果算法问题中涉及到的运算进行了多次重复,且参与运算的数前后有规律可循,就可以引入变量以参与循环结构.
3.在不同的循环结构中,应注意判断条件的差别及计数变量和累加(乘)变量的初值与运算框先后关系的对应性.
(2013·成都高一检测)设计求1×2×3×4×…×2
012的算法.
【解】 算法如下:
1.设m的值为1;
2.设i的值为2;
3.如果i≤2
012,则执行第四步,否则转去执行第六步;
4.计算m乘i并将结果赋给m;
5.计算i加1并将结果赋给i,转去执行第三步;
6.输出m的值并结束算法.
算法框图,如图所示:
类型2
代数运算问题的算法设计
画出求
的值的算法框图.
【思路探究】 (1)找循环变量i每次递增1,故只需式子i=i+1.
(2)设置循环体,观察这个数的特点是从里向外根号依次增多还多乘一个2,可以设置为A=.
(3)设置循环的终止条件i>5.
【自主解答】
1.这类比较特殊的数要注意找规律,本题的规律是对2开方,然后乘2再开方重复进行直到满足要求为止.
2.设计的关键是循环体的设置及循环的终止条件.
画出求(共6个2)的值的算法框图.
【解】 算法框图如下:
类型3
利用循环结构解决筛选问题
给出以下10个数:5,9,80,43,95,73,28,17,60,36,要求把大于40的数找出来并输出,试画出解决该问题的算法框图.
【思路探究】 可以考虑从第1个数开始与40比较大小,共需比较10次,可以设计一个计数变量来控制比较的次数.利用循环结构来设计算法.
【自主解答】
1.本题的算法设计中用了选择结构及循环结构.选择结构用于判断输入的数是否大于40,循环结构用于控制输入的数的个数.
2.在设计算法时,循环结构和选择结构可以综合应用.
(2012·课标全国卷)如果执行如图2-2-11所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )
图2-2-11
A.A+B为a1,a2,…,aN的和
B.为a1,a2,…,aN的算术平均数
C.A和B分别是a1,a2,…,aN中最大的数和最小的数
D.A和B分别是a1,a2,…,aN中最小的数和最大的数
【解析】 由于x=ak,且x>A时,将x值赋给A,因此最后输出的A值是a1,a2,…,aN中最大的数;由于x=ak,且x
忽略计数变量与循环次数致误
如图2-2-12,是某一算法的程序框图,根据该框图指出这一算法的功能.
图2-2-12
【错解】 求S=++++的值.
【错因分析】 本题忽略了计数变量与循环次数,没有明确循环体在循环结构中的作用,以及循环终止条件决定是否继续执行循环体.
【防范措施】 在循环过程中要明确循环的次数,明确起始数据和其后面数据的变化规律.
【正解】 在该程序框图中,S与n为两个累加变量,k为计数变量,所以该算法的功能是求+++…+的值.
1.设计一个算法框图算法的一般步骤
(1)用自然语言表述算法步骤;
(2)确定每一个算法步骤所包含的逻辑结构,并用相应的算法框图表示,得到表示该步骤的算法框图;
(3)将所有步骤的算法框图用流程线连接起来,并加上终端框,得到表示整个算法的算法框图.
2.循环结构的关键是要理解“累加变量”和“计数变量”,累加变量常用S表示,计数变量常用i表示.每循环一次,S和i都发生变化,根据判断框内的循环条件,直到中止循环为止.
1.如图2-2-13所示算法框图中的循环体是( )
图2-2-13
A.A B.C
C.ABCD
D.BD
【解析】 循环体是反复执行的部分,是BD,
故选D.
【答案】 D
2.(2013·天津高考)阅读如图2-2-14所示的程序框图,运行相应的程序.若输入x的值为1,则输出S的值为( )
图2-2-14
A.64 B.73 C.512 D.585
【解析】 程序框图执行过程如下:x=1,S=0,S=1,S<50 x=2,S=9,S<50 x=4,S=73>50,跳出循环,输出S=73.
【答案】 B
3.(2013·广东高考)执行如图2-2-15所示的程序框图,若输入n的值为4,则输出s的值为________.
图2-2-15
【解析】 第一步运算结果:s=1,i=2(i≤4成立);第二步运算结果:s=2,i=3(i≤4成立);第三步运算结果:s=4,i=4(i≤4成立);第四步运算结果:s=7,i=5(i≤4不成立),程序结束,故输出s的值为7.
【答案】 7
4.求1+2+3+4+…+110的值,写出算法步骤画出算法框图.
【解】 算法步骤:
(1)i=1,sum=0;
(2)sum=sum+i;
(3)i=i+1;
(4)如果i≤110,则执行第二步,否则执行下一步;
(5)输出sum.
算法框图如图所示:
一、选择题
1.(2013·重庆高考)执行如图2-2-16所示的程序框图,则输出的k的值是( )
图2-2-16
A.3 B.4 C.5 D.6
【解析】 k=1,s=1+02=1;k=2,s=1+12=2;k=3,s=2+22=6;k=4,s=6+32=15,k=5,s=15+42=31>15.故输出k=5,选C.
【答案】 C
2.(2013·辽宁高考)执行如图2-2-17所示的程序框图,若输入n=10,则输出S=( )
图2-2-17
A.
B.
C.
D.
【解析】 因为S=,i=4<10,所以S=+=,i=6<10,所以S=+=,i=8<10,所以S=+=,i=10=10,所以S=+=,i=12>10,输出S=.
【答案】 A
3.如图2-2-18所示框图表示的算法的功能是( )
图2-2-18
A.计算小于100的奇数的连乘积
B.计算从1开始的连续奇数的连乘积
C.从1开始的连续奇数的连乘积,当乘积大于100时,计算奇数的个数
D.计算1×3×5×7×…×n≥100时的最小的n值
【解析】 由框图知s=1×3×5×…×n.又因为循环结束的条件是s≥100,故其算法功能为:计算1×3×5×…×n≥100时的最小的n值.
【答案】 D
4.(2013·山东高考)执行两次如图2-2-19所示的程序框图,若第一次输入的a的值为-1.2,第二次输入的a的值为1.2,则第一次,第二次输出的a的值分别为( )
图2-2-19
A.0.2,0.2
B.0.2,0.8
C.0.8,0.2
D.0.8,0.8
【解析】 由程序框图可知:当a=-1.2时,∵a<0,
∴a=-1.2+1=-0.2,a<0,
a=-0.2+1=0.8,a>0.
∵0.8<1,输出a=0.8.
当a=1.2时,∵a≥1,
∴a=1.2-1=0.2.
∵0.2<1,输出a=0.2.
【答案】 C
图2-2-20
5.某算法框图如图2-2-20所示,若输出的S=57,则判断框内为( )
A.k>4 B.k>5
C.k>6
D.k>7
【解析】 k=1时,k=k+1=2,
S=2S+k=2×1+2=4;
k=2时,k=k+1=2+1=3,
S=2S+k=2×4+3=11;
k=3时,k=k+1=4,S=2S+k=2×11+4=26;
k=4时,k=k+1=5,S=2S+k=2×26+5=57.
此时S=57,循环结束,k=5,所以判断框内应填“k>4”,故选A.
【答案】 A
二、填空题(每小题5分,共10分)
6.(2013·江苏高考)如图是一个算法的流程图,则输出的n的值是________.
图2-2-21
【解析】 算法流程图执行过程如下:
n=1,a=2,a<20;
a=8,n=2,a<20;
a=26,n=3,a>20.
输出n=3.
【答案】 3
7.如图2-2-22所示的算法框图的功能是计算2×4×6×…×100的值,则处理框内应填________.
图2-2-22
【解析】 参与求积的因数皆为正偶数,故i的变化应保持始终是偶数,故i=i+2.
【答案】 i=i+2
8.如图2-2-23是统计该6名队员在最近三场比赛中投进的三分球总数的算法框图,则图中判断框应填________,输出的s=________.
图2-2-23
【解析】 观察算法框图可以看出,判断框内的条件满足时才执行循环体,所以判断框应填i≤6,输出的s是这6名队员成绩的和,即s=a1+a2+a3+a4+a5+a6.
【答案】 i≤6 a1+a2+a3+a4+a5+a6
三、解答题
9.计算下面的和:+++…+,画出其算法框图.
【解】 算法框图如图所示:
10.某高中男子体育小组的50
m赛跑成绩(单位:s)为6.4,6.5,7.0,6.8,7.1,7.3,6.9,7.4,7.5,7.6,6.3,6.4,6.4,6.5,6.7,7.1,6.9,6.4,7.1,7.0.设计一个算法,从这些成绩中搜索出小于6.8
s的成绩,并画出流程图.
【解】 体育小组共20人,要解决该问题必须对运动员进行编号,设第i个运动员编号为Ni,成绩为Gi.可以设计下面的算法.
算法如下:
第一步,i=1;
第二步,输入Ni,Gi;
第三步,如果Gi<6.8,则输出Ni、Gi,并执行第四步,否则,也执行第四步;
第四步,i=i+1;
第五步,如果i>20,则结束,否则返回第二步.
算法框图如图所示:
11.阅读如图2-2-24所示的算法框图,若输入n0=0,
则输出的结果为多少?
图2-2-24
【解】 当n0=0时,n=0,
n=n+1=0+1=1,
m==20∈N,且20≠1,所以输出m=20;
n=1+1=2,m==10,且10≠1,输出10;
n=2+1=3,m= N,
n=3+1=4,
m==5∈N,且5≠1,∴输出m=5;
n=4+1=5,m==4∈N,且4≠1,∴输出m=4;
n=6,7,8时均不输出,n=9时,n+1=10,m=2∈N,且2≠1,输出m=2.
n=11,12,13,14,15,16,17,18时均不输出,
n=19时,n+1=20,m=1∈N,结束.
∴综上,输出的结果为20,10,5,4,2.
