2.2.3 循环结构 学案3(含答案)
文档属性
| 名称 | 2.2.3 循环结构 学案3(含答案) | 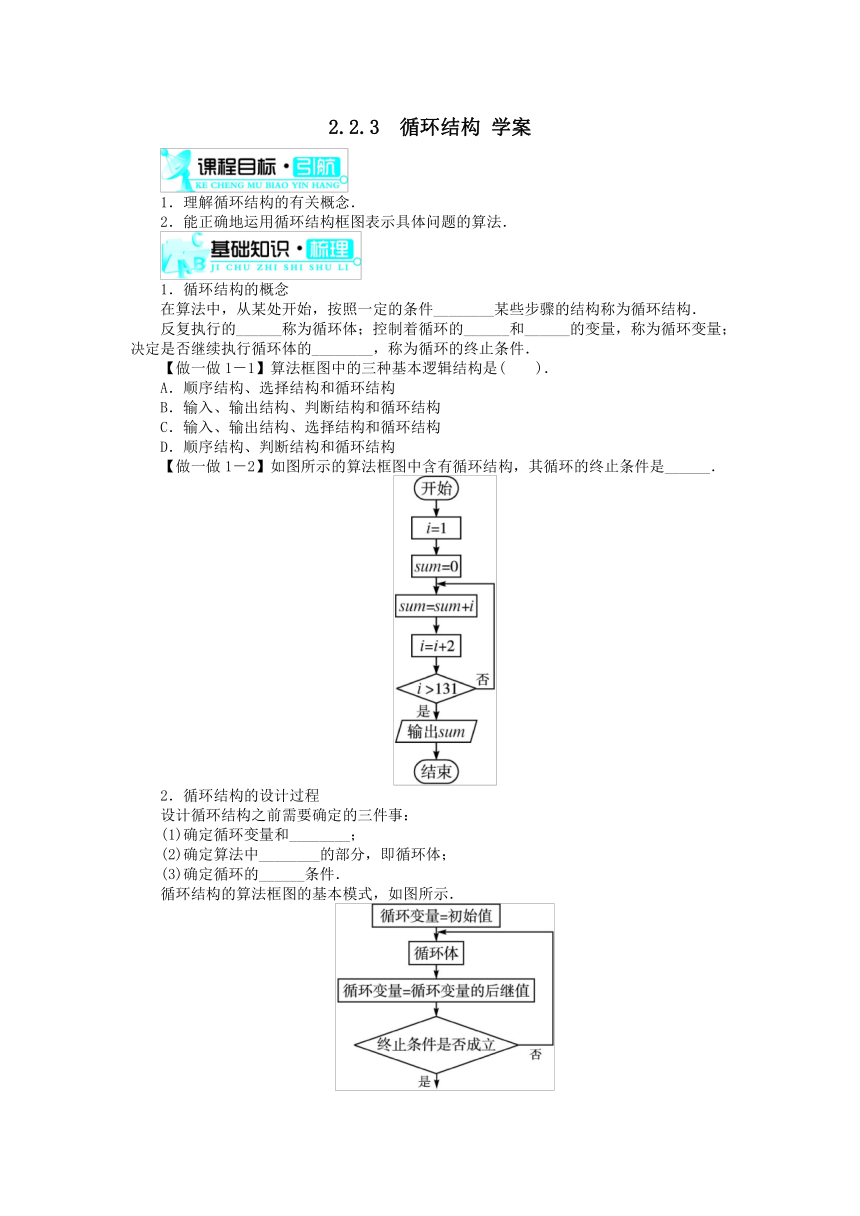 | |
| 格式 | zip | ||
| 文件大小 | 11.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-17 12:07:44 | ||
图片预览


文档简介
2.2.3 循环结构
学案
1.理解循环结构的有关概念.
2.能正确地运用循环结构框图表示具体问题的算法.
1.循环结构的概念
在算法中,从某处开始,按照一定的条件________某些步骤的结构称为循环结构.
反复执行的______称为循环体;控制着循环的______和______的变量,称为循环变量;决定是否继续执行循环体的________,称为循环的终止条件.
【做一做1-1】算法框图中的三种基本逻辑结构是( ).
A.顺序结构、选择结构和循环结构
B.输入、输出结构、判断结构和循环结构
C.输入、输出结构、选择结构和循环结构
D.顺序结构、判断结构和循环结构
【做一做1-2】如图所示的算法框图中含有循环结构,其循环的终止条件是______.
2.循环结构的设计过程
设计循环结构之前需要确定的三件事:
(1)确定循环变量和________;
(2)确定算法中________的部分,即循环体;
(3)确定循环的______条件.
循环结构的算法框图的基本模式,如图所示.
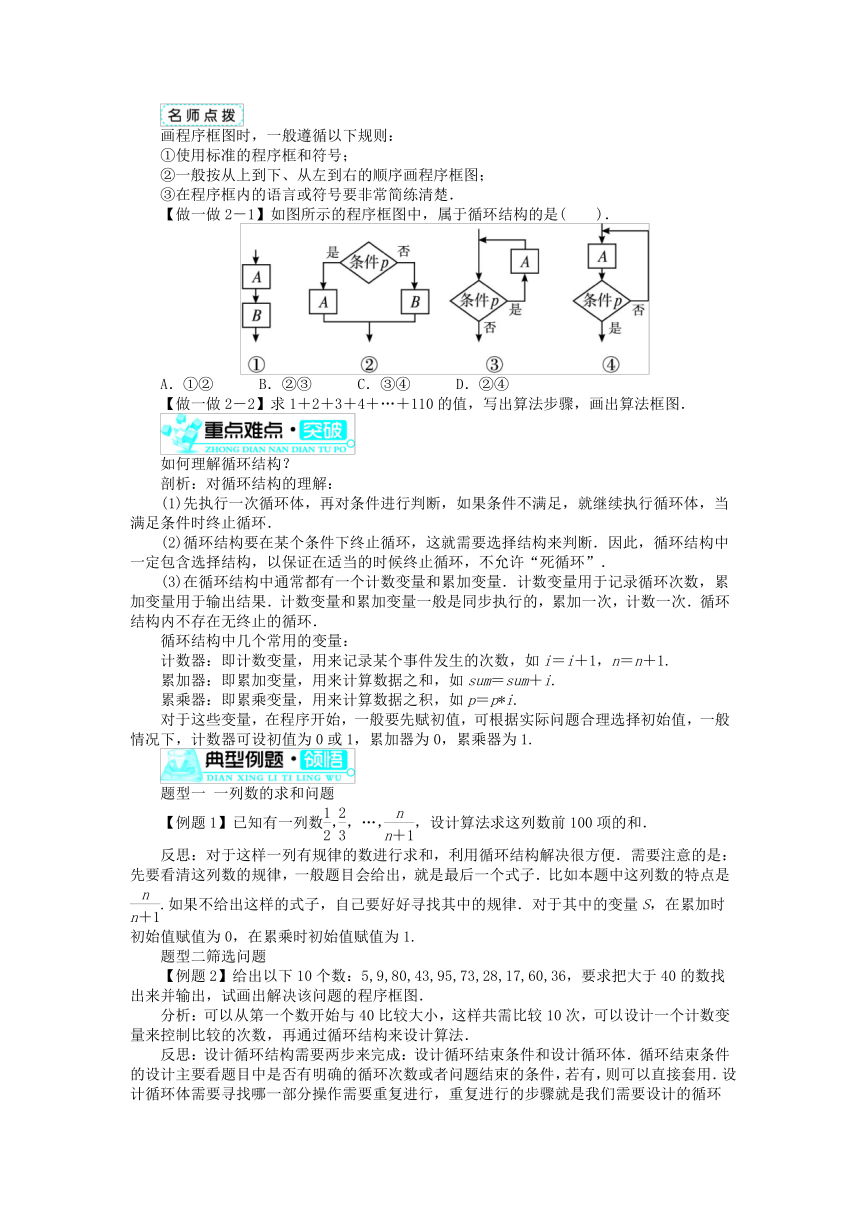
画程序框图时,一般遵循以下规则:
①使用标准的程序框和符号;
②一般按从上到下、从左到右的顺序画程序框图;
③在程序框内的语言或符号要非常简练清楚.
【做一做2-1】如图所示的程序框图中,属于循环结构的是( ).
A.①②
B.②③
C.③④
D.②④
【做一做2-2】求1+2+3+4+…+110的值,写出算法步骤,画出算法框图.
如何理解循环结构?
剖析:对循环结构的理解:
(1)先执行一次循环体,再对条件进行判断,如果条件不满足,就继续执行循环体,当满足条件时终止循环.
(2)循环结构要在某个条件下终止循环,这就需要选择结构来判断.因此,循环结构中一定包含选择结构,以保证在适当的时候终止循环,不允许“死循环”.
(3)在循环结构中通常都有一个计数变量和累加变量.计数变量用于记录循环次数,累加变量用于输出结果.计数变量和累加变量一般是同步执行的,累加一次,计数一次.循环结构内不存在无终止的循环.
循环结构中几个常用的变量:
计数器:即计数变量,用来记录某个事件发生的次数,如i=i+1,n=n+1.
累加器:即累加变量,用来计算数据之和,如sum=sum+i.
累乘器:即累乘变量,用来计算数据之积,如p=p
i.
对于这些变量,在程序开始,一般要先赋初值,可根据实际问题合理选择初始值,一般情况下,计数器可设初值为0或1,累加器为0,累乘器为1.
题型一
一列数的求和问题
【例题1】已知有一列数,,…,,设计算法求这列数前100项的和.
反思:对于这样一列有规律的数进行求和,利用循环结构解决很方便.需要注意的是:先要看清这列数的规律,一般题目会给出,就是最后一个式子.比如本题中这列数的特点是.如果不给出这样的式子,自己要好好寻找其中的规律.对于其中的变量S,在累加时初始值赋值为0,在累乘时初始值赋值为1.
题型二筛选问题
【例题2】给出以下10个数:5,9,80,43,95,73,28,17,60,36,要求把大于40的数找出来并输出,试画出解决该问题的程序框图.
分析:可以从第一个数开始与40比较大小,这样共需比较10次,可以设计一个计数变量来控制比较的次数,再通过循环结构来设计算法.
反思:设计循环结构需要两步来完成:设计循环结束条件和设计循环体.循环结束条件的设计主要看题目中是否有明确的循环次数或者问题结束的条件,若有,则可以直接套用.设计循环体需要寻找哪一部分操作需要重复进行,重复进行的步骤就是我们需要设计的循环体.
题型三
函数的求值问题
【例题3】已知函数f(x)=3x,设计输入x的值求f{f[f(x)]
}的值的算法,并画出程序框图.
分析:输入x后,将x代入函数f(x)求得函数值,再将函数值代回函数f(x),这个过程需重复进行,可以运用循环结构解决.
反思:本题解决的是函数求值问题,主要的难点是如何解决多次计算函数值的问题.每次求函数值的过程都是代入同一函数式,是重复的,需要重复3次,因此这部分可以考虑用循环结构.
题型四
易错辨析
【例题4】画出求1×3+2×4+3×5+4×6+5×7+6×8+7×9的值的程序框图.
错解:程序框图如图所示.
错因分析:第一处错误是判断框处,逻辑上为“是”时输出,“否”时应继续循环;第二处是循环体不对,不只是i=i+1,应包括S=S+i×(2+i).
1下列四个说法:
①任何一个算法都离不开顺序结构;
②算法框图中,根据条件是否成立有不同的流向;
③循环体是指按照一定条件,反复执行的某一处理步骤;
④循环结构中一定有选择结构,选择结构中一定有循环结构.
其中正确的个数为( ).
A.1
B.2
C.3
D.4
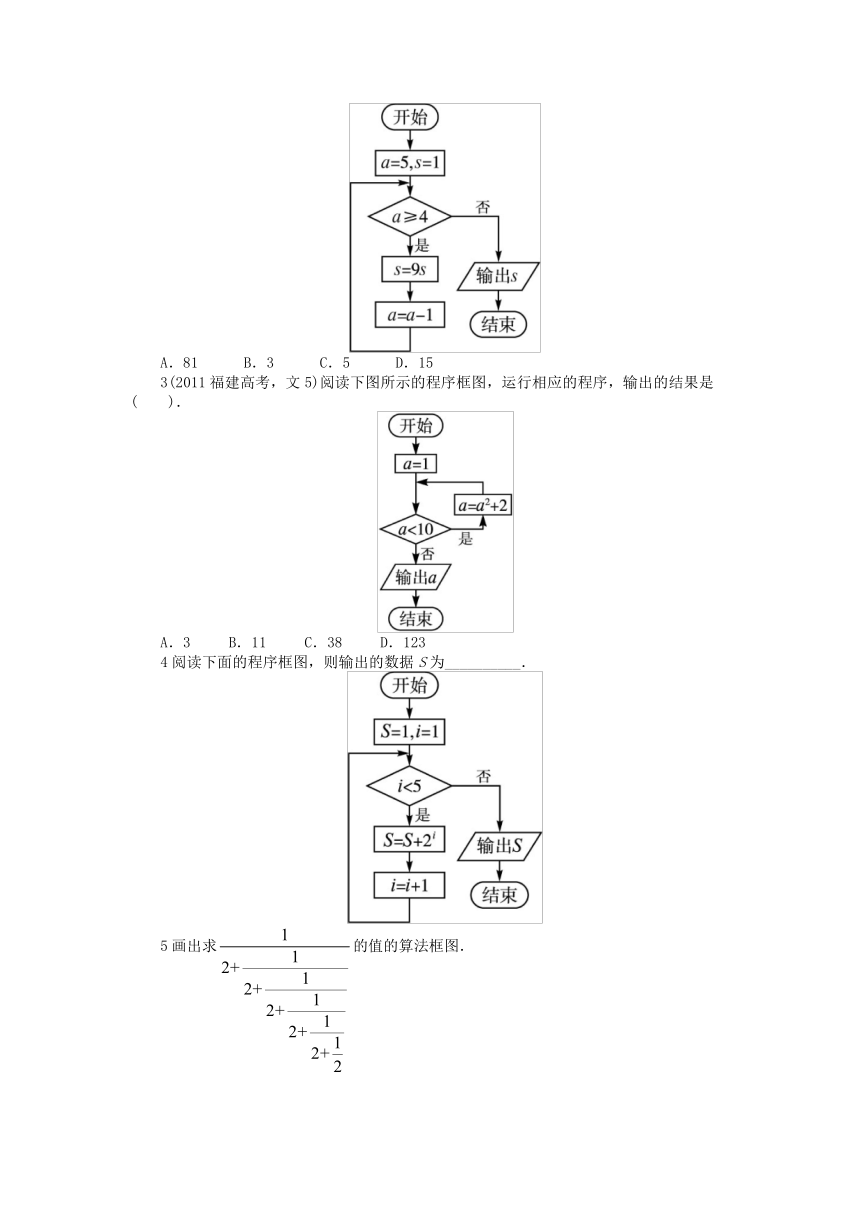
2阅读如图所示的算法框图,该算法框图输出的结果为( ).
A.81
B.3
C.5
D.15
3(2011福建高考,文5)阅读下图所示的程序框图,运行相应的程序,输出的结果是( ).
A.3
B.11
C.38
D.123
4阅读下面的程序框图,则输出的数据S为__________.
5画出求的值的算法框图.
答案:
基础知识·梳理
1.反复执行 步骤 开始 结束 判断条件
【做一做1-1】A
【做一做1-2】i>131
2.(1)初始条件 (2)反复执行 (3)终止
【做一做2-1】C ①是顺序结构;②中只是对条件的判断,不会重复出现操作;③④属于循环结构.
【做一做2-2】分析:由于重复做加法,因此需用循环结构.
解:算法步骤:
1.i=1,sum=0;
2.sum=sum+i;
3.i=i+1;
4.如果i≤110,则执行第二步,否则执行下一步;
5.输出sum.
算法框图如图所示.
典型例题·领悟
【例题1】解:1.找循环变量i,其增量为1,故只需用式子i=i+1;
2.设置循环体,观察这列数的特点是,将这样的数累加S=S+;
3.设置循环终止的条件i>100,算法框图如图.
【例题2】解:程序框图如图所示.
【例题3】解:算法如下:
1.输入x;
2.i=1;
3.若i≤3,则y=3x,x=y,i=i+1,继续执行第3步;否则,执行第4步;
4.输出y.
程序框图如图所示.
【例题4】正解:程序框图如图所示.
随堂练习·巩固
1.C ①②③正确,④错误,故选C.
2.A 第一次循环,s=9,a=4;
第二次循环,s=81,a=3<4.
故循环终止,输出s=81.故选A.
3.B 第一次循环,a=3;第二次循环,a=11,故该程序框图运行后输出的结果为11.
4.31 S=1+21+22+23+24=31.
5.分析:这个式子实际上是通过求和,取倒数;再求和,取倒数,反复5次即可达到目的.循环变量为i,初始值为1,每次递增1;循环体为A=;循环的终止条件为i>5.
解:算法框图如图所示.
学案
1.理解循环结构的有关概念.
2.能正确地运用循环结构框图表示具体问题的算法.
1.循环结构的概念
在算法中,从某处开始,按照一定的条件________某些步骤的结构称为循环结构.
反复执行的______称为循环体;控制着循环的______和______的变量,称为循环变量;决定是否继续执行循环体的________,称为循环的终止条件.
【做一做1-1】算法框图中的三种基本逻辑结构是( ).
A.顺序结构、选择结构和循环结构
B.输入、输出结构、判断结构和循环结构
C.输入、输出结构、选择结构和循环结构
D.顺序结构、判断结构和循环结构
【做一做1-2】如图所示的算法框图中含有循环结构,其循环的终止条件是______.
2.循环结构的设计过程
设计循环结构之前需要确定的三件事:
(1)确定循环变量和________;
(2)确定算法中________的部分,即循环体;
(3)确定循环的______条件.
循环结构的算法框图的基本模式,如图所示.
画程序框图时,一般遵循以下规则:
①使用标准的程序框和符号;
②一般按从上到下、从左到右的顺序画程序框图;
③在程序框内的语言或符号要非常简练清楚.
【做一做2-1】如图所示的程序框图中,属于循环结构的是( ).
A.①②
B.②③
C.③④
D.②④
【做一做2-2】求1+2+3+4+…+110的值,写出算法步骤,画出算法框图.
如何理解循环结构?
剖析:对循环结构的理解:
(1)先执行一次循环体,再对条件进行判断,如果条件不满足,就继续执行循环体,当满足条件时终止循环.
(2)循环结构要在某个条件下终止循环,这就需要选择结构来判断.因此,循环结构中一定包含选择结构,以保证在适当的时候终止循环,不允许“死循环”.
(3)在循环结构中通常都有一个计数变量和累加变量.计数变量用于记录循环次数,累加变量用于输出结果.计数变量和累加变量一般是同步执行的,累加一次,计数一次.循环结构内不存在无终止的循环.
循环结构中几个常用的变量:
计数器:即计数变量,用来记录某个事件发生的次数,如i=i+1,n=n+1.
累加器:即累加变量,用来计算数据之和,如sum=sum+i.
累乘器:即累乘变量,用来计算数据之积,如p=p
i.
对于这些变量,在程序开始,一般要先赋初值,可根据实际问题合理选择初始值,一般情况下,计数器可设初值为0或1,累加器为0,累乘器为1.
题型一
一列数的求和问题
【例题1】已知有一列数,,…,,设计算法求这列数前100项的和.
反思:对于这样一列有规律的数进行求和,利用循环结构解决很方便.需要注意的是:先要看清这列数的规律,一般题目会给出,就是最后一个式子.比如本题中这列数的特点是.如果不给出这样的式子,自己要好好寻找其中的规律.对于其中的变量S,在累加时初始值赋值为0,在累乘时初始值赋值为1.
题型二筛选问题
【例题2】给出以下10个数:5,9,80,43,95,73,28,17,60,36,要求把大于40的数找出来并输出,试画出解决该问题的程序框图.
分析:可以从第一个数开始与40比较大小,这样共需比较10次,可以设计一个计数变量来控制比较的次数,再通过循环结构来设计算法.
反思:设计循环结构需要两步来完成:设计循环结束条件和设计循环体.循环结束条件的设计主要看题目中是否有明确的循环次数或者问题结束的条件,若有,则可以直接套用.设计循环体需要寻找哪一部分操作需要重复进行,重复进行的步骤就是我们需要设计的循环体.
题型三
函数的求值问题
【例题3】已知函数f(x)=3x,设计输入x的值求f{f[f(x)]
}的值的算法,并画出程序框图.
分析:输入x后,将x代入函数f(x)求得函数值,再将函数值代回函数f(x),这个过程需重复进行,可以运用循环结构解决.
反思:本题解决的是函数求值问题,主要的难点是如何解决多次计算函数值的问题.每次求函数值的过程都是代入同一函数式,是重复的,需要重复3次,因此这部分可以考虑用循环结构.
题型四
易错辨析
【例题4】画出求1×3+2×4+3×5+4×6+5×7+6×8+7×9的值的程序框图.
错解:程序框图如图所示.
错因分析:第一处错误是判断框处,逻辑上为“是”时输出,“否”时应继续循环;第二处是循环体不对,不只是i=i+1,应包括S=S+i×(2+i).
1下列四个说法:
①任何一个算法都离不开顺序结构;
②算法框图中,根据条件是否成立有不同的流向;
③循环体是指按照一定条件,反复执行的某一处理步骤;
④循环结构中一定有选择结构,选择结构中一定有循环结构.
其中正确的个数为( ).
A.1
B.2
C.3
D.4
2阅读如图所示的算法框图,该算法框图输出的结果为( ).
A.81
B.3
C.5
D.15
3(2011福建高考,文5)阅读下图所示的程序框图,运行相应的程序,输出的结果是( ).
A.3
B.11
C.38
D.123
4阅读下面的程序框图,则输出的数据S为__________.
5画出求的值的算法框图.
答案:
基础知识·梳理
1.反复执行 步骤 开始 结束 判断条件
【做一做1-1】A
【做一做1-2】i>131
2.(1)初始条件 (2)反复执行 (3)终止
【做一做2-1】C ①是顺序结构;②中只是对条件的判断,不会重复出现操作;③④属于循环结构.
【做一做2-2】分析:由于重复做加法,因此需用循环结构.
解:算法步骤:
1.i=1,sum=0;
2.sum=sum+i;
3.i=i+1;
4.如果i≤110,则执行第二步,否则执行下一步;
5.输出sum.
算法框图如图所示.
典型例题·领悟
【例题1】解:1.找循环变量i,其增量为1,故只需用式子i=i+1;
2.设置循环体,观察这列数的特点是,将这样的数累加S=S+;
3.设置循环终止的条件i>100,算法框图如图.
【例题2】解:程序框图如图所示.
【例题3】解:算法如下:
1.输入x;
2.i=1;
3.若i≤3,则y=3x,x=y,i=i+1,继续执行第3步;否则,执行第4步;
4.输出y.
程序框图如图所示.
【例题4】正解:程序框图如图所示.
随堂练习·巩固
1.C ①②③正确,④错误,故选C.
2.A 第一次循环,s=9,a=4;
第二次循环,s=81,a=3<4.
故循环终止,输出s=81.故选A.
3.B 第一次循环,a=3;第二次循环,a=11,故该程序框图运行后输出的结果为11.
4.31 S=1+21+22+23+24=31.
5.分析:这个式子实际上是通过求和,取倒数;再求和,取倒数,反复5次即可达到目的.循环变量为i,初始值为1,每次递增1;循环体为A=;循环的终止条件为i>5.
解:算法框图如图所示.
