2.3.1 条件语句 教案1
图片预览


文档简介
2.3.1
条件语句
教案
(教师用书独具)
●三维目标
1.知识与技能
理解条件语句和条件结构之间的对应关系.
掌握条件语句的语法规则和用算法解决问题的一般步骤.
提高学生逻辑思维能力,发展有条理的思考与表达能力.
2.过程与方法
教师设置情境,引导学生提出问题这一过程,培养学生的创造性思维.
写算法步骤,画程序框图,编写程序,QBasic实现算法这一解决问题的步骤,培养理性精神和实践能力.
通过小组合作交流,更深层次理解算法的基本思想.
3.情感、态度与价值观
利用QBasic实现算法,提高学生学习兴趣,树立学好数学的信心.
认识数学的价值,培养学生良好的个性品质,形成积极的学习态度.
●重点难点
重点:条件语句的格式、结构;用所学算法语句解决问题的过程和方法.
难点:利用条件语句编写解决问题的程序;用QBasic实现算法.
(教师用书独具)
●教学建议
教师可以在教学过程中通过不断地提出问题,促进学生深入思考.发挥学生主体地位,辅以多媒体手段,引导学生主动参与,自主探究,小组交流合作探索研究问题的学习方法.
●教学流程
创设情境,形成问题,以家庭固定电话收费标准为实例,如何写出其算法语言 引导学生设计算法,画出算法框图,分析结构特征明确选择结构的特点,引出条件语句的格式 通过例1及变式训练,使学生掌握条件语句与选择结构的关系,进一步理解条件语句的格式及特征 通过例2及其变式训练,使学生能够运用复合If语句进行简单的设计,进一步巩固三种语句的特点及复合If条件语句的运用
在掌握条件语句与选择结构的基础上,通过例3掌握条件语句的实际应用,使学生的能力得到提升 归纳整理,进行课堂小结,整体认识本节课所学知识,分层布置作业使不同层次的学生有不同的收获 完成当堂双基达标,巩固所学知识并进行反馈,矫正
课标解读
1.正确理解条件语句的概念.2.能应用条件语句描述算法(重点).3.能应用条件语句编写程序(难点).
知识1
条件语句
【问题导思】
某居民区的物管部门每月按如下方法收取卫生费:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元,令c(单位:元)表示应收取的费用,n表示某户人家的人数.
1.试写出根据输入人数计算应收取卫生费的函数关系式.
【提示】 c=
2.画出解决该问题的算法框图.
【提示】
在算法中,选择结构是一种基本结构,条件语句是表达选择结构最常用的语句.
知识2
If语句
形如下面的框图描述的算法都可以用If语句进行表示.
其一般形式是:
知识3
复合If语句
形如下面的框图描述的算法都可以用复合If语句来表达.
复合If语句的一般形式是:
类型1
条件语句的简单应用
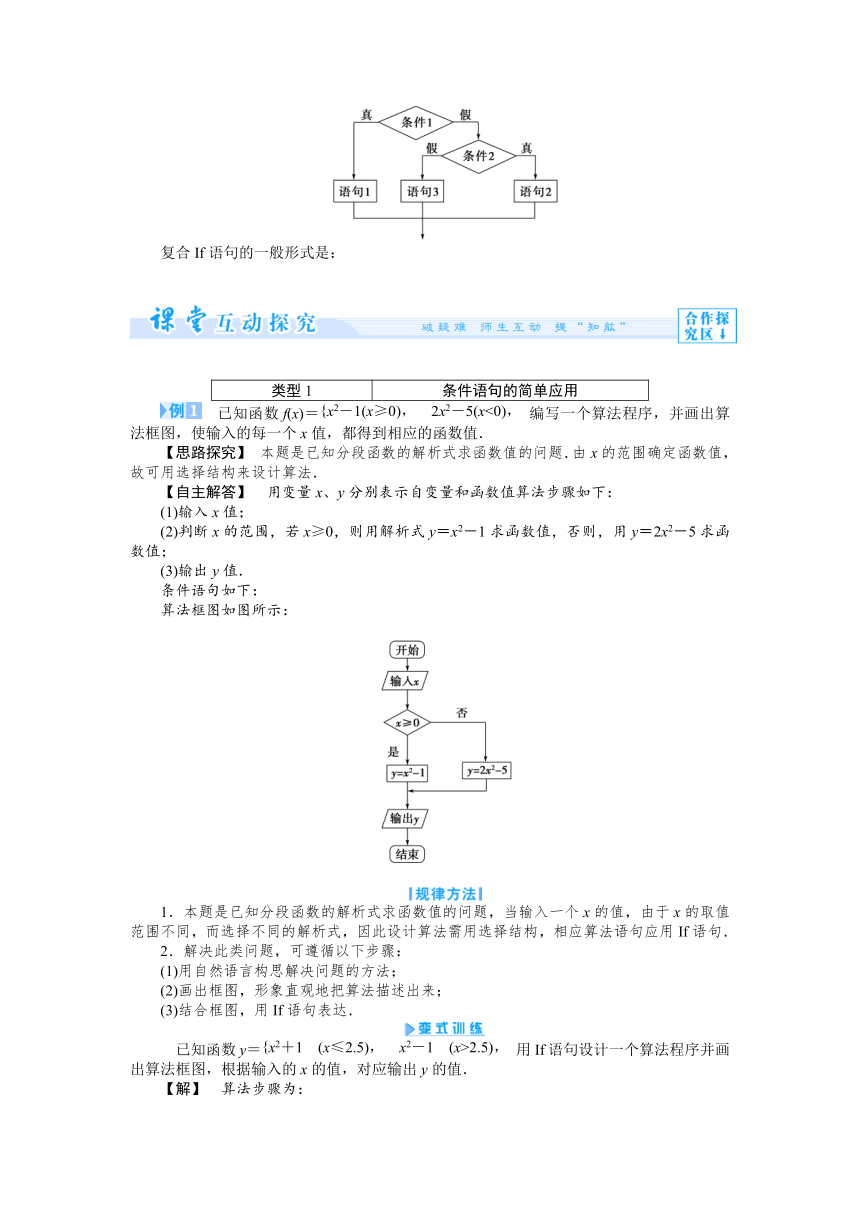
已知函数f(x)=编写一个算法程序,并画出算法框图,使输入的每一个x值,都得到相应的函数值.
【思路探究】 本题是已知分段函数的解析式求函数值的问题.由x的范围确定函数值,故可用选择结构来设计算法.
【自主解答】 用变量x、y分别表示自变量和函数值算法步骤如下:
(1)输入x值;
(2)判断x的范围,若x≥0,则用解析式y=x2-1求函数值,否则,用y=2x2-5求函数值;
(3)输出y值.
条件语句如下:
算法框图如图所示:
1.本题是已知分段函数的解析式求函数值的问题,当输入一个x的值,由于x的取值范围不同,而选择不同的解析式,因此设计算法需用选择结构,相应算法语句应用If语句.
2.解决此类问题,可遵循以下步骤:
(1)用自然语言构思解决问题的方法;
(2)画出框图,形象直观地把算法描述出来;
(3)结合框图,用If语句表达.
已知函数y=用If语句设计一个算法程序并画出算法框图,根据输入的x的值,对应输出y的值.
【解】 算法步骤为:
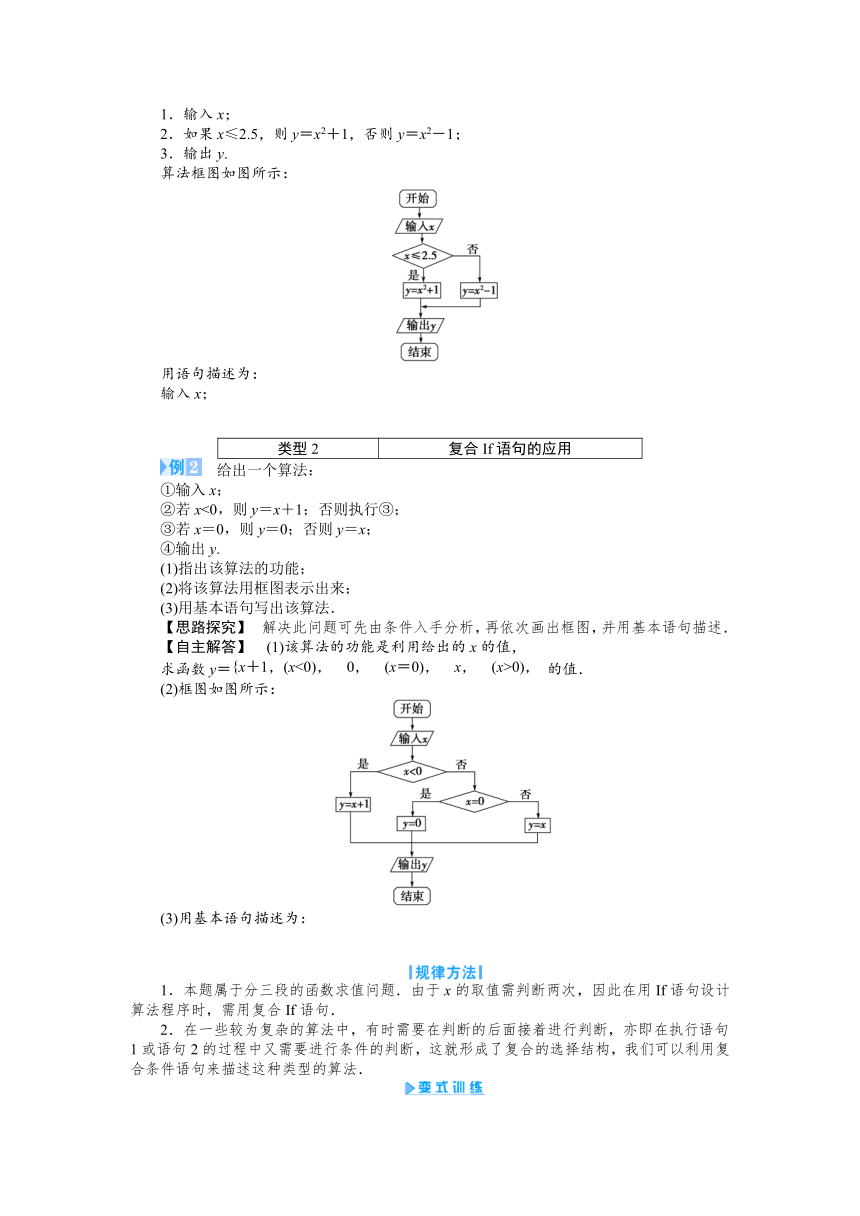
1.输入x;
2.如果x≤2.5,则y=x2+1,否则y=x2-1;
3.输出y.
算法框图如图所示:
用语句描述为:
输入x;
类型2
复合If语句的应用
给出一个算法:
①输入x;
②若x<0,则y=x+1;否则执行③;
③若x=0,则y=0;否则y=x;
④输出y.
(1)指出该算法的功能;
(2)将该算法用框图表示出来;
(3)用基本语句写出该算法.
【思路探究】 解决此问题可先由条件入手分析,再依次画出框图,并用基本语句描述.
【自主解答】 (1)该算法的功能是利用给出的x的值,
求函数y=的值.
(2)框图如图所示:
(3)用基本语句描述为:
1.本题属于分三段的函数求值问题.由于x的取值需判断两次,因此在用If语句设计算法程序时,需用复合If语句.
2.在一些较为复杂的算法中,有时需要在判断的后面接着进行判断,亦即在执行语句1或语句2的过程中又需要进行条件的判断,这就形成了复合的选择结构,我们可以利用复合条件语句来描述这种类型的算法.
已知函数f(x)=试编写算法语句,根据输入的x值输出对应的y值.
【解】 输入x;
类型3
条件语句的实际应用
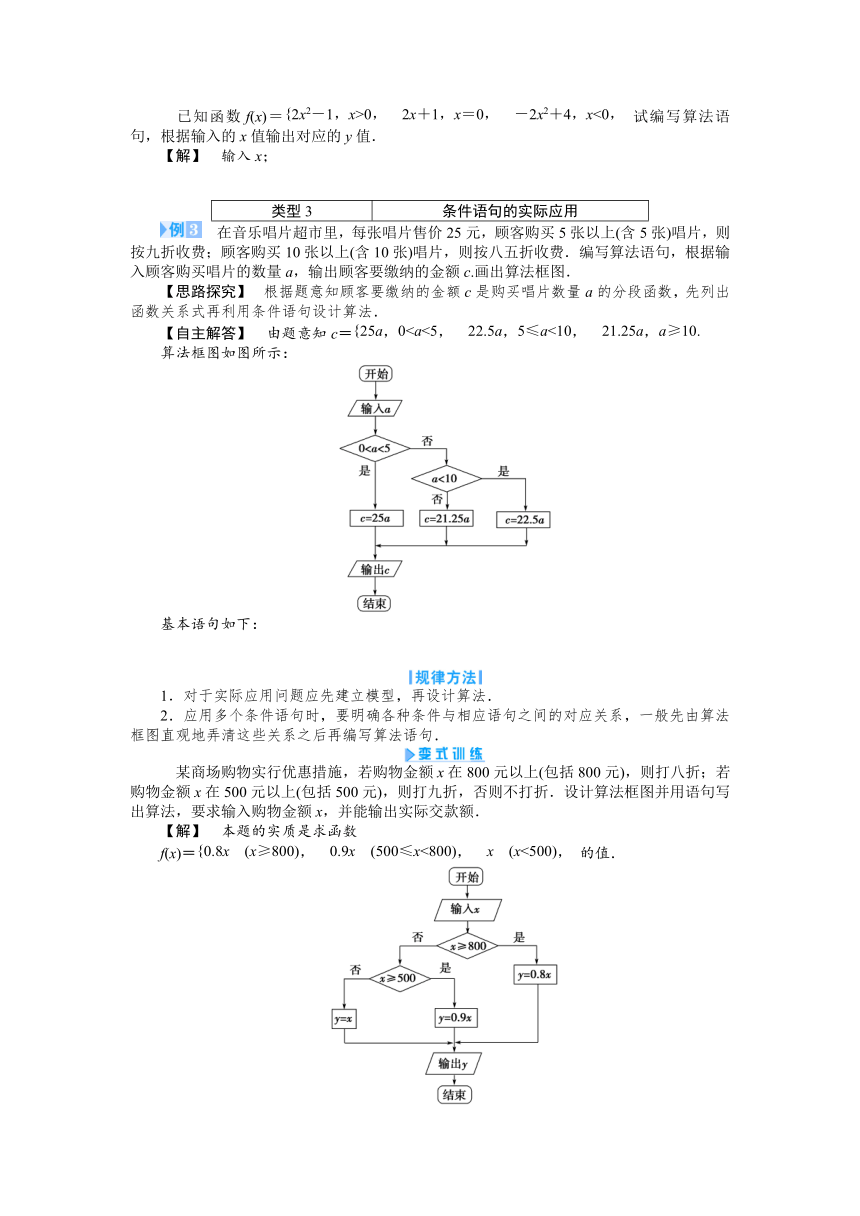
在音乐唱片超市里,每张唱片售价25元,顾客购买5张以上(含5张)唱片,则按九折收费;顾客购买10张以上(含10张)唱片,则按八五折收费.编写算法语句,根据输入顾客购买唱片的数量a,输出顾客要缴纳的金额c.画出算法框图.
【思路探究】 根据题意知顾客要缴纳的金额c是购买唱片数量a的分段函数,先列出函数关系式再利用条件语句设计算法.
【自主解答】 由题意知c=
算法框图如图所示:
基本语句如下:
1.对于实际应用问题应先建立模型,再设计算法.
2.应用多个条件语句时,要明确各种条件与相应语句之间的对应关系,一般先由算法框图直观地弄清这些关系之后再编写算法语句.
某商场购物实行优惠措施,若购物金额x在800元以上(包括800元),则打八折;若购物金额x在500元以上(包括500元),则打九折,否则不打折.设计算法框图并用语句写出算法,要求输入购物金额x,并能输出实际交款额.
【解】 本题的实质是求函数
f(x)=的值.
用语句描述如下:
输入x;
复合If语句结构不明确致误
(2013·西安检测)设计一个基本语句求y=的值.
【错解】 用语句描述如下:
输入x;
【错因分析】 在条件语句中,复合If语句最后一定有两个End
If.
【防范措施】 1.理解并掌握条件语句的结构特点.
2.写条件语句时要正确分类且做到不重不漏,它有严格的格式和用法,否则无法运行.
【正解】 用语句描述如下:
输入x;
使用条件语句应注意的问题
(1)条件语句是一个语句,If、Else、End
If都是语句的一部分.
(2)条件语句必须以If语句开始,以End
If语句结束,一个If语句必须和一个End
If语句对应.
(3)如果我们的程序只需对条件为真的情况作出处理,不需要处理条件为假的情况,则条件语句省略Else分句,格式由If—Else—End
If语句变成If—End
If语句.
(4)应用多个条件语句即复合If语句时,要明确各种条件与相应语句之间的对应关系,一般先由算法框图直观地弄清这些关系之后再编写程序.
1.下列函数求值算法中需要用到条件语句的函数为( )
A.f(x)=x2-1 B.y=x3-1
C.f(x)=
D.f(x)=logax
【解析】 解决一个问题时,若不需要判断,则不需要用条件语句.A、B、D均直接求解即可.
【答案】 C
2.执行下面的算法,若输入3,则输出的y的值是( )
A.3 B.7 C.9 D.19
【解析】 x=3,由于3>3不成立,所以执行Else后面的语句,即y=2×3+1=7.
故输出y=7,所以选B.
【答案】 B
3.写出下面语句运算的结果
输入a;
If a<0 Then
输出 不存在
Else
t=
输出t
Ene
If
当a=-5时,输出结果为________,当a=9时输出结果为________.
【解析】 该算法语句的功能为若a≥0,
则输出t=,
若a<0,则输出“不存在”,
故当a=-5时,输出的结果为“不存在”,
当a=9时,输出的结果为t==3.
【答案】 不存在 3
4.将下列算法框图转化为算法语句.
图2-3-1
【解】 算法语句如下:
一、选择题
1.为了在运行下面的算法语句之后输出y=9,键盘输入应该是( )
输入x;
A.x=-4 B.x=-2
C.x=4或-4
D.x=2或-2
【解析】 当x<0时,由(x+1)(x+1)=9得x=-4,
当x≥0时,由(x-1)(x-1)=9得x=4,∴x=4或-4.
【答案】 C
2.以下算法语句运行的结果为( )
A.0
B.2 C.4 D.-4
【解析】 运行过程中m=2,a=-2,b=2,因为a≤b,所以x=a+b=0.
【答案】 A
3.阅读下列语句:
如果输出5,则输入的a为( )
A.2.5 B.2
C.-2
D.±2
【解析】 由算法语句可知,令2a=5,则a=<5(舍).令a2+1=5,
则a=±2,满足题意.
【答案】 D
4.下列算法语句运行的结果是( )
A=4.5
B=6
A.10.5 B.11.5 C.16 D.25
【解析】 A=4.5<5,∴B=6-3=3,B=3+2=5.
又5≥4,∴B=52=25.
【答案】 D
5.对于条件语句的描述正确的是( )
A.执行下列条件语句时,当不满足条件时,执行语句1,满足条件时执行语句2
If 条件 Then
语句1
Else
语句2
End
If
B.执行下列条件语句时,如果满足条件,那么就执行Then后的语句,如果不满足条件,那么就直接结束该条件语句,转而执行其他语句
If 条件 Then
语句
End
If
C.条件语句在程序中能够减少大量烦琐的计算
D.条件语句中不能有输出语句
【解析】 A中,如果满足条件,那么就执行语句1,否则执行语句2,所以A不正确;条件语句在程序中起判断转折作用,不能减少大量烦琐的计算,所以C不正确;条件语句中可以有输出语句,所以D不正确.
【答案】 B
二、填空题
6.下列程序的功能是:判断任意输入的数x是否是正数,若是,输出它的平方值;若不是,输出它的相反数.
输入x;
则填入的条件应该是________.
【解析】 由程序的功能和If语句可知,If后面的条件应填x≤0.
【答案】 x≤0
7.写出下列程序运行结果.
若输入x=6,则p=________;
若输入x=18,则p=________.
【解析】 x=6时,p=6×0.35=2.1;
x=18时,p=10×0.35+8×0.7=9.1.
【答案】 2.1 9.1
8.若运行如下语句,最后输出y的值为-20,那么应该输入t的值为________.
输入t;
【解析】 可得如下分段函数y=
当2t-8=-20,∴t=-6,合题意;
当8t-t2=-20,∴t2-8t-20=0,∴t=10,
或t=-2(舍),故t=-6或10.
【答案】 -6或10
三、解答题
9.用基本算法语句描述一个算法,要求输入两个实数,然后由小到大输出这两个数.
【解】 算法语句为:
10.下面是计算应纳税所得额的算法过程,其算法如下:
第一步:输入工资x(注x≤5
000);
第二步:如果x≤2
000,那么y=0;
如果2
000500,
那么y=0.05(x-2
000);
否则y=25+0.1(x-2
500);
第三步:输出税款y,结束.
请写出该算法的算法框图和相应的算法语句.
【解】 算法框图如下:
算法语句为:
输入x;
11.根据下面的框图回答后面的问题.
(1)用语句描述其算法;
(2)研究框图,回答:
①当输入的x值为1时,输出的y值为多少?
②要使输出的y值为10,输入的x值应该为多少?
③输入的x值和输出的y值可能相等吗?若能,x的输入值为多少?若不能,说明理由.
图2-3-2
【解】 (1)用语句描述算法如下:
输入x;
(2)①当x=1时,∵1≤3,∴y=2×1=2,∴输出的y是2.
②由2x=10得x=5>3(舍),
由2x+2=10,知x=4.
∵4>3,∴要使输出的值为10,输入的应为4.
③可能相等.当输入的x=0时,y=2x=0,输入的x值和输出y值相等.
当2x+2=x即x=-2时,虽然有y=x,但-2<3,此时不可能.
综上,当输入的x=0时,输入值x和输出值y相等.
(教师用书独具)
某次考试规定:共考三门课,凡考试符合下列条件之一的,发给优秀证书.
①三门成绩之和大于280分;
②其中两门成绩大于95分,另一门成绩大于80分.
试编写一个算法语句.
【解】 用语句描述如下:
输入学生的考试成绩a,b,c;
If a+b+c>280 Then
输出“请发给优秀证书!”
Else
If a>95 And b>95 And c>80 Then
输出“请发给优秀证书!”
Else
If b>95 And c>95 And a>80 Then
输出“请发给优秀证书!”
Else
If a>95 And c>95 And b>80 Then
输出“请发给优秀证书!”
Else
输出“不发给优秀证书!”
End
If
End
If
End
If
End
If
乘坐火车时,可以托运货物.从甲地到乙地,规定每张火车客票托运费计算方法是:行李质量不超过50
kg时按0.25元/kg;超过50
kg而不超过100
kg时,其超过部分按0.35元/kg;超过100
kg时,其超过部分按0.45元/kg.设计算法语句,输入行李质量,计算出托运的费用.
【解】 设行李质量为x
kg,应付运费为y元,则运费公式为
y=
整理,得
y=
要计算托运的费用,必须对行李质量分类讨论,因此要用条件语句来实现.
算法步骤:
1.输入行李质量x;
2.当x≤50时,计算y=0.25x,否则执行下一步;
3.当x≤100时,计算y=0.35x-5,否则计算y=0.45x-15;
4.输出y.
算法框图,如下图:
条件语句
教案
(教师用书独具)
●三维目标
1.知识与技能
理解条件语句和条件结构之间的对应关系.
掌握条件语句的语法规则和用算法解决问题的一般步骤.
提高学生逻辑思维能力,发展有条理的思考与表达能力.
2.过程与方法
教师设置情境,引导学生提出问题这一过程,培养学生的创造性思维.
写算法步骤,画程序框图,编写程序,QBasic实现算法这一解决问题的步骤,培养理性精神和实践能力.
通过小组合作交流,更深层次理解算法的基本思想.
3.情感、态度与价值观
利用QBasic实现算法,提高学生学习兴趣,树立学好数学的信心.
认识数学的价值,培养学生良好的个性品质,形成积极的学习态度.
●重点难点
重点:条件语句的格式、结构;用所学算法语句解决问题的过程和方法.
难点:利用条件语句编写解决问题的程序;用QBasic实现算法.
(教师用书独具)
●教学建议
教师可以在教学过程中通过不断地提出问题,促进学生深入思考.发挥学生主体地位,辅以多媒体手段,引导学生主动参与,自主探究,小组交流合作探索研究问题的学习方法.
●教学流程
创设情境,形成问题,以家庭固定电话收费标准为实例,如何写出其算法语言 引导学生设计算法,画出算法框图,分析结构特征明确选择结构的特点,引出条件语句的格式 通过例1及变式训练,使学生掌握条件语句与选择结构的关系,进一步理解条件语句的格式及特征 通过例2及其变式训练,使学生能够运用复合If语句进行简单的设计,进一步巩固三种语句的特点及复合If条件语句的运用
在掌握条件语句与选择结构的基础上,通过例3掌握条件语句的实际应用,使学生的能力得到提升 归纳整理,进行课堂小结,整体认识本节课所学知识,分层布置作业使不同层次的学生有不同的收获 完成当堂双基达标,巩固所学知识并进行反馈,矫正
课标解读
1.正确理解条件语句的概念.2.能应用条件语句描述算法(重点).3.能应用条件语句编写程序(难点).
知识1
条件语句
【问题导思】
某居民区的物管部门每月按如下方法收取卫生费:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元,令c(单位:元)表示应收取的费用,n表示某户人家的人数.
1.试写出根据输入人数计算应收取卫生费的函数关系式.
【提示】 c=
2.画出解决该问题的算法框图.
【提示】
在算法中,选择结构是一种基本结构,条件语句是表达选择结构最常用的语句.
知识2
If语句
形如下面的框图描述的算法都可以用If语句进行表示.
其一般形式是:
知识3
复合If语句
形如下面的框图描述的算法都可以用复合If语句来表达.
复合If语句的一般形式是:
类型1
条件语句的简单应用
已知函数f(x)=编写一个算法程序,并画出算法框图,使输入的每一个x值,都得到相应的函数值.
【思路探究】 本题是已知分段函数的解析式求函数值的问题.由x的范围确定函数值,故可用选择结构来设计算法.
【自主解答】 用变量x、y分别表示自变量和函数值算法步骤如下:
(1)输入x值;
(2)判断x的范围,若x≥0,则用解析式y=x2-1求函数值,否则,用y=2x2-5求函数值;
(3)输出y值.
条件语句如下:
算法框图如图所示:
1.本题是已知分段函数的解析式求函数值的问题,当输入一个x的值,由于x的取值范围不同,而选择不同的解析式,因此设计算法需用选择结构,相应算法语句应用If语句.
2.解决此类问题,可遵循以下步骤:
(1)用自然语言构思解决问题的方法;
(2)画出框图,形象直观地把算法描述出来;
(3)结合框图,用If语句表达.
已知函数y=用If语句设计一个算法程序并画出算法框图,根据输入的x的值,对应输出y的值.
【解】 算法步骤为:
1.输入x;
2.如果x≤2.5,则y=x2+1,否则y=x2-1;
3.输出y.
算法框图如图所示:
用语句描述为:
输入x;
类型2
复合If语句的应用
给出一个算法:
①输入x;
②若x<0,则y=x+1;否则执行③;
③若x=0,则y=0;否则y=x;
④输出y.
(1)指出该算法的功能;
(2)将该算法用框图表示出来;
(3)用基本语句写出该算法.
【思路探究】 解决此问题可先由条件入手分析,再依次画出框图,并用基本语句描述.
【自主解答】 (1)该算法的功能是利用给出的x的值,
求函数y=的值.
(2)框图如图所示:
(3)用基本语句描述为:
1.本题属于分三段的函数求值问题.由于x的取值需判断两次,因此在用If语句设计算法程序时,需用复合If语句.
2.在一些较为复杂的算法中,有时需要在判断的后面接着进行判断,亦即在执行语句1或语句2的过程中又需要进行条件的判断,这就形成了复合的选择结构,我们可以利用复合条件语句来描述这种类型的算法.
已知函数f(x)=试编写算法语句,根据输入的x值输出对应的y值.
【解】 输入x;
类型3
条件语句的实际应用
在音乐唱片超市里,每张唱片售价25元,顾客购买5张以上(含5张)唱片,则按九折收费;顾客购买10张以上(含10张)唱片,则按八五折收费.编写算法语句,根据输入顾客购买唱片的数量a,输出顾客要缴纳的金额c.画出算法框图.
【思路探究】 根据题意知顾客要缴纳的金额c是购买唱片数量a的分段函数,先列出函数关系式再利用条件语句设计算法.
【自主解答】 由题意知c=
算法框图如图所示:
基本语句如下:
1.对于实际应用问题应先建立模型,再设计算法.
2.应用多个条件语句时,要明确各种条件与相应语句之间的对应关系,一般先由算法框图直观地弄清这些关系之后再编写算法语句.
某商场购物实行优惠措施,若购物金额x在800元以上(包括800元),则打八折;若购物金额x在500元以上(包括500元),则打九折,否则不打折.设计算法框图并用语句写出算法,要求输入购物金额x,并能输出实际交款额.
【解】 本题的实质是求函数
f(x)=的值.
用语句描述如下:
输入x;
复合If语句结构不明确致误
(2013·西安检测)设计一个基本语句求y=的值.
【错解】 用语句描述如下:
输入x;
【错因分析】 在条件语句中,复合If语句最后一定有两个End
If.
【防范措施】 1.理解并掌握条件语句的结构特点.
2.写条件语句时要正确分类且做到不重不漏,它有严格的格式和用法,否则无法运行.
【正解】 用语句描述如下:
输入x;
使用条件语句应注意的问题
(1)条件语句是一个语句,If、Else、End
If都是语句的一部分.
(2)条件语句必须以If语句开始,以End
If语句结束,一个If语句必须和一个End
If语句对应.
(3)如果我们的程序只需对条件为真的情况作出处理,不需要处理条件为假的情况,则条件语句省略Else分句,格式由If—Else—End
If语句变成If—End
If语句.
(4)应用多个条件语句即复合If语句时,要明确各种条件与相应语句之间的对应关系,一般先由算法框图直观地弄清这些关系之后再编写程序.
1.下列函数求值算法中需要用到条件语句的函数为( )
A.f(x)=x2-1 B.y=x3-1
C.f(x)=
D.f(x)=logax
【解析】 解决一个问题时,若不需要判断,则不需要用条件语句.A、B、D均直接求解即可.
【答案】 C
2.执行下面的算法,若输入3,则输出的y的值是( )
A.3 B.7 C.9 D.19
【解析】 x=3,由于3>3不成立,所以执行Else后面的语句,即y=2×3+1=7.
故输出y=7,所以选B.
【答案】 B
3.写出下面语句运算的结果
输入a;
If a<0 Then
输出 不存在
Else
t=
输出t
Ene
If
当a=-5时,输出结果为________,当a=9时输出结果为________.
【解析】 该算法语句的功能为若a≥0,
则输出t=,
若a<0,则输出“不存在”,
故当a=-5时,输出的结果为“不存在”,
当a=9时,输出的结果为t==3.
【答案】 不存在 3
4.将下列算法框图转化为算法语句.
图2-3-1
【解】 算法语句如下:
一、选择题
1.为了在运行下面的算法语句之后输出y=9,键盘输入应该是( )
输入x;
A.x=-4 B.x=-2
C.x=4或-4
D.x=2或-2
【解析】 当x<0时,由(x+1)(x+1)=9得x=-4,
当x≥0时,由(x-1)(x-1)=9得x=4,∴x=4或-4.
【答案】 C
2.以下算法语句运行的结果为( )
A.0
B.2 C.4 D.-4
【解析】 运行过程中m=2,a=-2,b=2,因为a≤b,所以x=a+b=0.
【答案】 A
3.阅读下列语句:
如果输出5,则输入的a为( )
A.2.5 B.2
C.-2
D.±2
【解析】 由算法语句可知,令2a=5,则a=<5(舍).令a2+1=5,
则a=±2,满足题意.
【答案】 D
4.下列算法语句运行的结果是( )
A=4.5
B=6
A.10.5 B.11.5 C.16 D.25
【解析】 A=4.5<5,∴B=6-3=3,B=3+2=5.
又5≥4,∴B=52=25.
【答案】 D
5.对于条件语句的描述正确的是( )
A.执行下列条件语句时,当不满足条件时,执行语句1,满足条件时执行语句2
If 条件 Then
语句1
Else
语句2
End
If
B.执行下列条件语句时,如果满足条件,那么就执行Then后的语句,如果不满足条件,那么就直接结束该条件语句,转而执行其他语句
If 条件 Then
语句
End
If
C.条件语句在程序中能够减少大量烦琐的计算
D.条件语句中不能有输出语句
【解析】 A中,如果满足条件,那么就执行语句1,否则执行语句2,所以A不正确;条件语句在程序中起判断转折作用,不能减少大量烦琐的计算,所以C不正确;条件语句中可以有输出语句,所以D不正确.
【答案】 B
二、填空题
6.下列程序的功能是:判断任意输入的数x是否是正数,若是,输出它的平方值;若不是,输出它的相反数.
输入x;
则填入的条件应该是________.
【解析】 由程序的功能和If语句可知,If后面的条件应填x≤0.
【答案】 x≤0
7.写出下列程序运行结果.
若输入x=6,则p=________;
若输入x=18,则p=________.
【解析】 x=6时,p=6×0.35=2.1;
x=18时,p=10×0.35+8×0.7=9.1.
【答案】 2.1 9.1
8.若运行如下语句,最后输出y的值为-20,那么应该输入t的值为________.
输入t;
【解析】 可得如下分段函数y=
当2t-8=-20,∴t=-6,合题意;
当8t-t2=-20,∴t2-8t-20=0,∴t=10,
或t=-2(舍),故t=-6或10.
【答案】 -6或10
三、解答题
9.用基本算法语句描述一个算法,要求输入两个实数,然后由小到大输出这两个数.
【解】 算法语句为:
10.下面是计算应纳税所得额的算法过程,其算法如下:
第一步:输入工资x(注x≤5
000);
第二步:如果x≤2
000,那么y=0;
如果2
000
那么y=0.05(x-2
000);
否则y=25+0.1(x-2
500);
第三步:输出税款y,结束.
请写出该算法的算法框图和相应的算法语句.
【解】 算法框图如下:
算法语句为:
输入x;
11.根据下面的框图回答后面的问题.
(1)用语句描述其算法;
(2)研究框图,回答:
①当输入的x值为1时,输出的y值为多少?
②要使输出的y值为10,输入的x值应该为多少?
③输入的x值和输出的y值可能相等吗?若能,x的输入值为多少?若不能,说明理由.
图2-3-2
【解】 (1)用语句描述算法如下:
输入x;
(2)①当x=1时,∵1≤3,∴y=2×1=2,∴输出的y是2.
②由2x=10得x=5>3(舍),
由2x+2=10,知x=4.
∵4>3,∴要使输出的值为10,输入的应为4.
③可能相等.当输入的x=0时,y=2x=0,输入的x值和输出y值相等.
当2x+2=x即x=-2时,虽然有y=x,但-2<3,此时不可能.
综上,当输入的x=0时,输入值x和输出值y相等.
(教师用书独具)
某次考试规定:共考三门课,凡考试符合下列条件之一的,发给优秀证书.
①三门成绩之和大于280分;
②其中两门成绩大于95分,另一门成绩大于80分.
试编写一个算法语句.
【解】 用语句描述如下:
输入学生的考试成绩a,b,c;
If a+b+c>280 Then
输出“请发给优秀证书!”
Else
If a>95 And b>95 And c>80 Then
输出“请发给优秀证书!”
Else
If b>95 And c>95 And a>80 Then
输出“请发给优秀证书!”
Else
If a>95 And c>95 And b>80 Then
输出“请发给优秀证书!”
Else
输出“不发给优秀证书!”
End
If
End
If
End
If
End
If
乘坐火车时,可以托运货物.从甲地到乙地,规定每张火车客票托运费计算方法是:行李质量不超过50
kg时按0.25元/kg;超过50
kg而不超过100
kg时,其超过部分按0.35元/kg;超过100
kg时,其超过部分按0.45元/kg.设计算法语句,输入行李质量,计算出托运的费用.
【解】 设行李质量为x
kg,应付运费为y元,则运费公式为
y=
整理,得
y=
要计算托运的费用,必须对行李质量分类讨论,因此要用条件语句来实现.
算法步骤:
1.输入行李质量x;
2.当x≤50时,计算y=0.25x,否则执行下一步;
3.当x≤100时,计算y=0.35x-5,否则计算y=0.45x-15;
4.输出y.
算法框图,如下图:
