新人教数学八年级下16.3分式方程第一课时
文档属性
| 名称 | 新人教数学八年级下16.3分式方程第一课时 |

|
|
| 格式 | rar | ||
| 文件大小 | 574.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-16 00:00:00 | ||
图片预览








文档简介
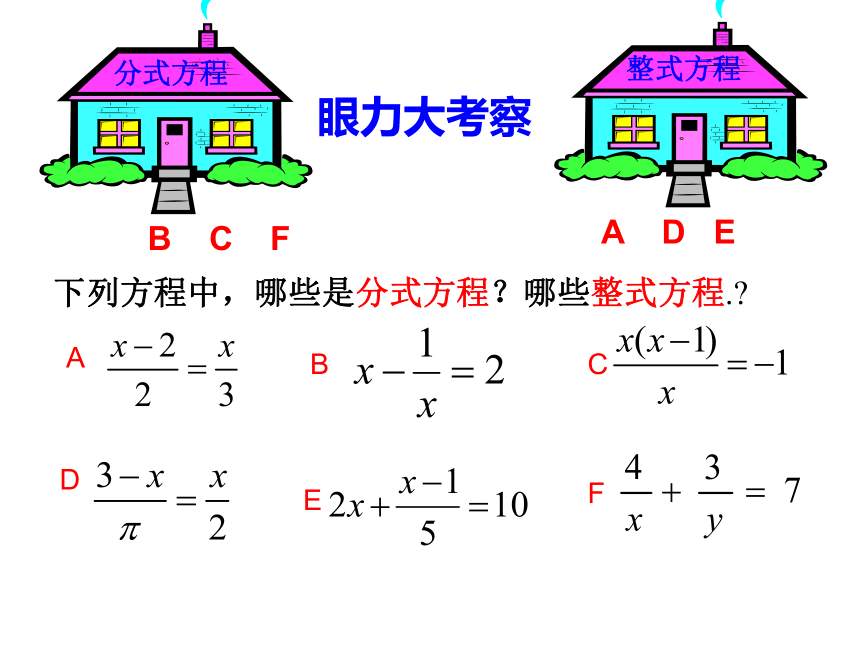
课件20张PPT。16.3分式方程亲爱的同学们:
花香鸟语春天事,北大清华少年心. 点燃激情,放飞梦想, 展现自我,活出精彩.今天的目标:1.理解分式方程的概念.
2.理解分式方程的解题思路.
3.掌握解分式方程的一般步骤.
4.体会转化思想方法.重点提醒:分式方程的概念、分式方程的解题思路和解分式方程的一般步骤。难点突破:分式方程产生增根的原因及对增根的理解。 一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?解:设江水的流速为 v 千米/时.分母中含未知数探究一本章引言中的问题:这个方程与以前学过的方程有什么不同?议一议根据题意得:分式方程像这样,分母里含有未知数的方程叫做分式方程。以前学过的分母里不含有未知数的方程叫做整式方程。整式方程分式方程A BCDEFB C FA D E下列方程中,哪些是分式方程?哪些整式方程.?眼力大考察 解得:如何解分式方程? 解:方程两边同乘以(20+v)(20-v) 得:检验: 将v=5代入分式方程,左边=4=右边, 所以v=5是原分式方程的解。探究二 你能结合探究活动归纳出解分式方程的基本思路和做法吗?你如何确定v=5一定是分式方程的解?试一试1.解分式方程的基本思路是:将分式方程转化为整式方程.再解整式方程.
2.化整方法:方程两边同时乘各分母的最简公分母.
3.这种数学思想方法把它叫做“转化”数学思想。归纳:解分式方程:解:方程两边同乘以最简公分母(x-5)(x+5)得:x+5=10解得:x=5检验: 将x=5代入原方程 x-5 ,x2-25的值都为0,相应分式无意义. 原分式方程无解。试一试x=5一定是分式方程的解吗?为什么?所以x=5不是原分式方程的解。 分式方程去分母所得整式方程的解就是①的解.分式方程
去分母后所得整式方程的解却不是②的解呢?
探究三 解分式方程去分母时,方程两边要同乘以一个含未知数的式子(最简公分母).方程①两边同乘以一个不为0的整式.方程②两边同乘以一个为0的整式.想一想原因: 在去分母时,将分式方程转化为整式方程的过程中出现的不适合于原方程的解原因是: 分式方程两边同乘以一个零因式后,所得的根是整式方程的解,而不是分式方程的解.所以我们解分式方程时一定要检验········这个解使最简公分母的值为零·········归纳:检验的方法:1.整式方程的解代入最简公分母, 如果最简公分母值不为0, 则整式方程的解是原分式方程的解.否则,这个解不是原分式方程的解.2.代入原方程,看左右两边是否相等.分式方程整式方程解整式方程检 验转化例:解分式方程解下列分式方程(1)(2)挑战自我解分式方程的一般步骤是: 1.在方程的两边都乘以最简公分母,化为整式方程.
2.解这个整式方程.
3. 把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解.否则,这个解不是原分式方程的解,必须舍去.
4.写出原方程的解.解分式方程的思路是:分式方程整式方程去分母一化整二解方程三检验解方程:随堂练习解分式方程容易犯的错误有:(1)去分母时,原方程的整式部分漏乘.(2)约去分母后,分子是多项式时,要 注意添括号.(因分数线有括号的作用) (3)忘记检验。 必须检验 2、如果 有增根,那么增根为 .x=21、关于x的方程 =4 的解是x= , 则a= .2拓展练习3、若分式方程 有增根x=2,则 a= .-1温馨提示: 增根是去分母后整式方程的解,不是原分式方程的解.拓展练习4.若方程 会产生增根,
则( )
A、k=±2 B、k=2
C、k=-2 D、k为任何实数温馨提示:使最简公分母的值为零解叫做增根我今天的收获1.认识了分式方程.
2.学会解分式方程: 一化二解三检验.
3.领悟到数学思想方法是:转化的思想方法.再 见!
花香鸟语春天事,北大清华少年心. 点燃激情,放飞梦想, 展现自我,活出精彩.今天的目标:1.理解分式方程的概念.
2.理解分式方程的解题思路.
3.掌握解分式方程的一般步骤.
4.体会转化思想方法.重点提醒:分式方程的概念、分式方程的解题思路和解分式方程的一般步骤。难点突破:分式方程产生增根的原因及对增根的理解。 一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?解:设江水的流速为 v 千米/时.分母中含未知数探究一本章引言中的问题:这个方程与以前学过的方程有什么不同?议一议根据题意得:分式方程像这样,分母里含有未知数的方程叫做分式方程。以前学过的分母里不含有未知数的方程叫做整式方程。整式方程分式方程A BCDEFB C FA D E下列方程中,哪些是分式方程?哪些整式方程.?眼力大考察 解得:如何解分式方程? 解:方程两边同乘以(20+v)(20-v) 得:检验: 将v=5代入分式方程,左边=4=右边, 所以v=5是原分式方程的解。探究二 你能结合探究活动归纳出解分式方程的基本思路和做法吗?你如何确定v=5一定是分式方程的解?试一试1.解分式方程的基本思路是:将分式方程转化为整式方程.再解整式方程.
2.化整方法:方程两边同时乘各分母的最简公分母.
3.这种数学思想方法把它叫做“转化”数学思想。归纳:解分式方程:解:方程两边同乘以最简公分母(x-5)(x+5)得:x+5=10解得:x=5检验: 将x=5代入原方程 x-5 ,x2-25的值都为0,相应分式无意义. 原分式方程无解。试一试x=5一定是分式方程的解吗?为什么?所以x=5不是原分式方程的解。 分式方程去分母所得整式方程的解就是①的解.分式方程
去分母后所得整式方程的解却不是②的解呢?
探究三 解分式方程去分母时,方程两边要同乘以一个含未知数的式子(最简公分母).方程①两边同乘以一个不为0的整式.方程②两边同乘以一个为0的整式.想一想原因: 在去分母时,将分式方程转化为整式方程的过程中出现的不适合于原方程的解原因是: 分式方程两边同乘以一个零因式后,所得的根是整式方程的解,而不是分式方程的解.所以我们解分式方程时一定要检验········这个解使最简公分母的值为零·········归纳:检验的方法:1.整式方程的解代入最简公分母, 如果最简公分母值不为0, 则整式方程的解是原分式方程的解.否则,这个解不是原分式方程的解.2.代入原方程,看左右两边是否相等.分式方程整式方程解整式方程检 验转化例:解分式方程解下列分式方程(1)(2)挑战自我解分式方程的一般步骤是: 1.在方程的两边都乘以最简公分母,化为整式方程.
2.解这个整式方程.
3. 把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解.否则,这个解不是原分式方程的解,必须舍去.
4.写出原方程的解.解分式方程的思路是:分式方程整式方程去分母一化整二解方程三检验解方程:随堂练习解分式方程容易犯的错误有:(1)去分母时,原方程的整式部分漏乘.(2)约去分母后,分子是多项式时,要 注意添括号.(因分数线有括号的作用) (3)忘记检验。 必须检验 2、如果 有增根,那么增根为 .x=21、关于x的方程 =4 的解是x= , 则a= .2拓展练习3、若分式方程 有增根x=2,则 a= .-1温馨提示: 增根是去分母后整式方程的解,不是原分式方程的解.拓展练习4.若方程 会产生增根,
则( )
A、k=±2 B、k=2
C、k=-2 D、k为任何实数温馨提示:使最简公分母的值为零解叫做增根我今天的收获1.认识了分式方程.
2.学会解分式方程: 一化二解三检验.
3.领悟到数学思想方法是:转化的思想方法.再 见!
