抛物线及其标准方程课件
图片预览




文档简介
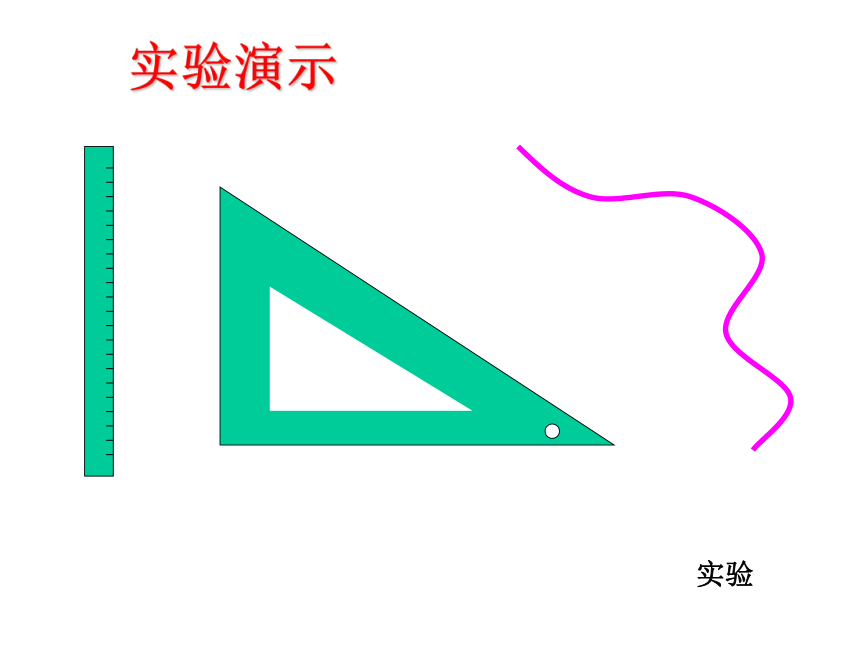
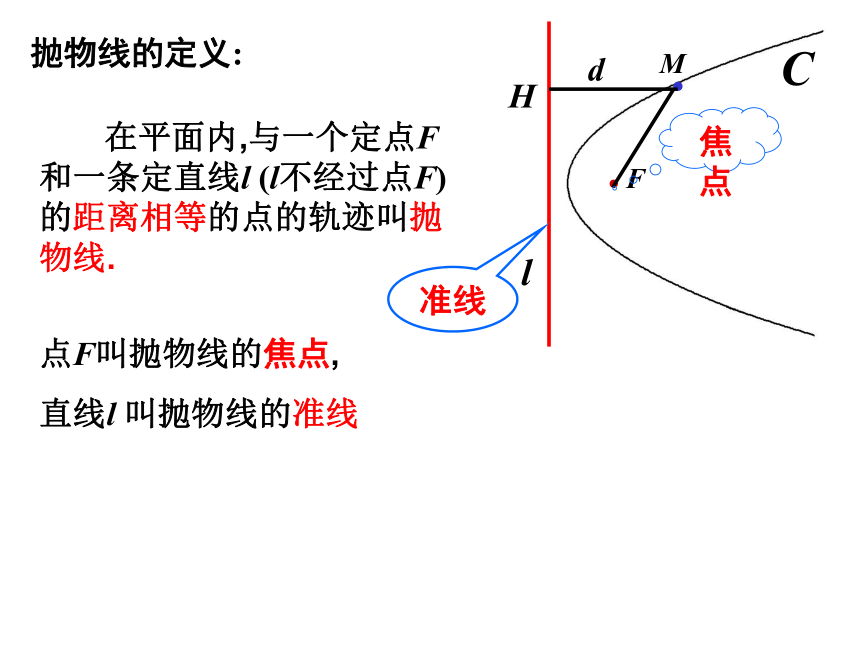
课件25张PPT。抛物线及其标准方程(一)抛物线及其标准方程(一)实验演示实验M·Fl· 在平面内,与一个定点F和一条定直线l (l不经过点F)的距离相等的点的轨迹叫抛物线.点F叫抛物线的焦点,
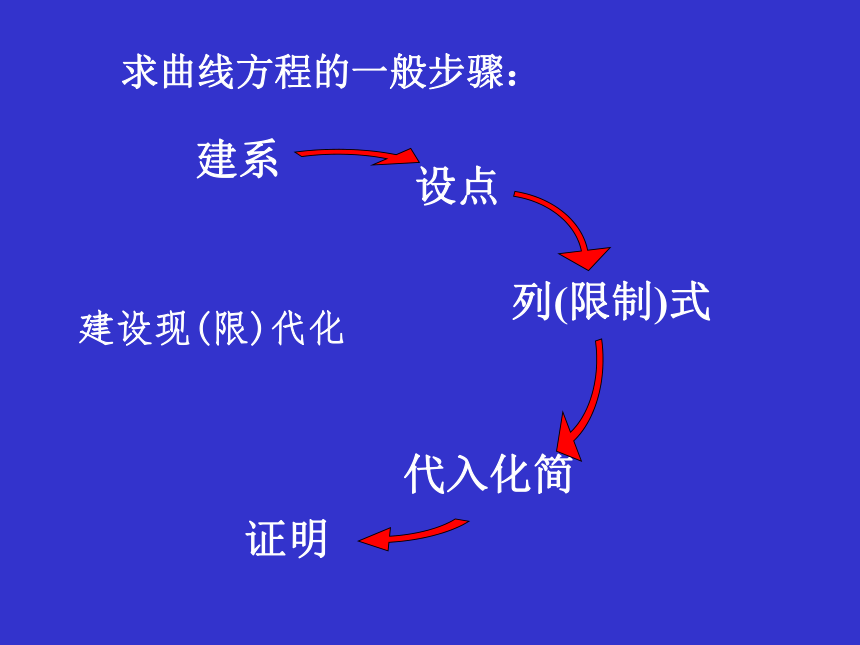
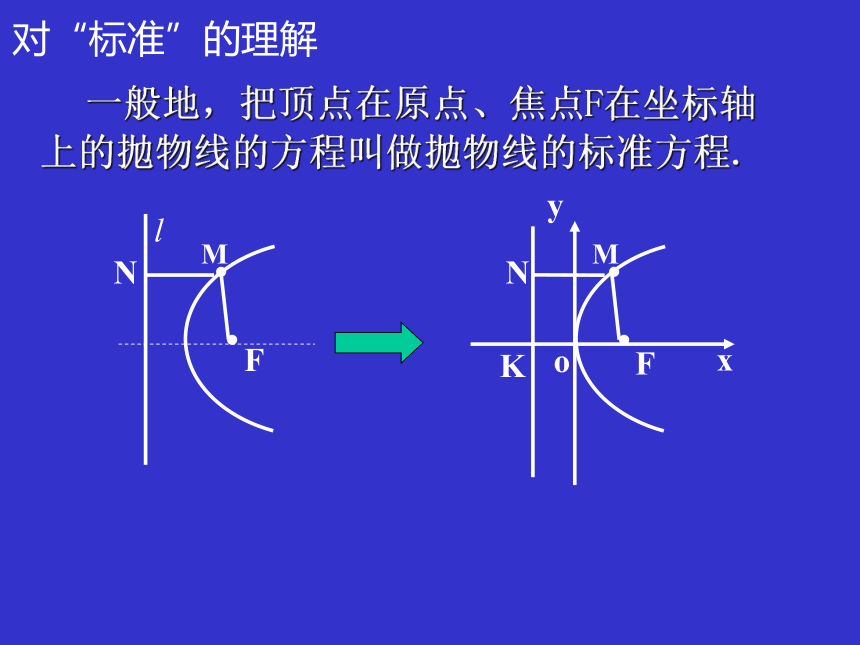
直线l 叫抛物线的准线准线焦点d抛物线的定义:求曲线方程的一般步骤:·方案1方案2方案3抛物线的标准方程 把方程 y2 = 2px (p>0)叫做抛物线的标准方程.其中 p 为正常数. p的几何意义是:焦点坐标是准线方程为:焦点到准线的距离对“标准”的理解 一般地,把顶点在原点、焦点F在坐标轴上的抛物线的方程叫做抛物线的标准方程.
MxMl向右
向左
向上
向下
yx例题1、(1)已知抛物线的标准方程是 y 2 = 6 x ,求它的焦点坐标及准线方程(2)已知抛物线的焦点坐标是 F(0,-2),求抛物线的标准方程x 2 =-8 y图象小结数形结合的思想。题后反思:小结生活中的抛物线---喷泉生活中的抛物线---赵州桥卫星天线生活中的抛物线例2:一种卫星接收天线的轴截面如下图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处。已知接收天线的径口(直径)为4.8m,深度为0.5m。建立适当的坐标系,求抛物线的标准方程和焦点坐标。小结解:如上图,在接收天线的轴截面所在平面内建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合。 即
所以,所求抛物线的标准方程是 ,焦点的坐标是小结:1、抛物线的定义和四种标准方程的形式2、抛物线的标准方程与图象之间的特征关系3、数形结合的思想方法o返回解:(2)因为焦点在 y 轴的负半轴上,并且 = 2,p = 4 ,所以所求抛物线的标准方程是 x2 =-8y .
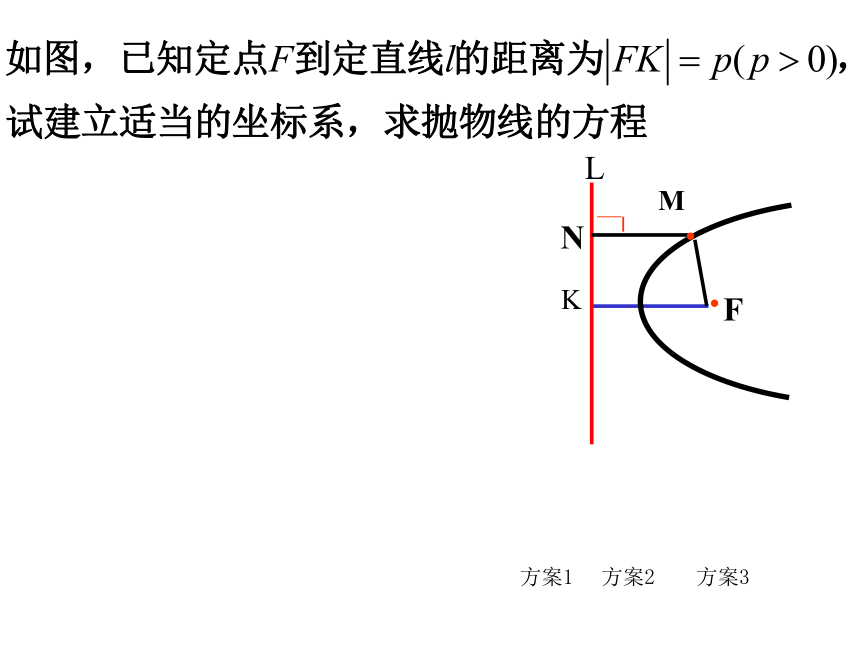
yoFN··x方案:以l为y轴,过点F且垂直于l的直线为x轴
建立直角坐标系,则点F(p ,0).设动点M(x,y),由抛物线定义得M(x,y)方案3比较方案:以定点F为原点,过点F且垂直于l的直线为x轴建立直角坐标系.yKFMN··x设动点M(x,y),由抛物线定义得则点F(0 ,0), l 的方程为x= -- p .l比较方案1比较l方案:以过F且垂直于 l 的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xoy.M(x,y)F两边平方,整理得这就是所求的轨迹方程.N依题意得方案1方案2三种建系方案比较标准方程
直线l 叫抛物线的准线准线焦点d抛物线的定义:求曲线方程的一般步骤:·方案1方案2方案3抛物线的标准方程 把方程 y2 = 2px (p>0)叫做抛物线的标准方程.其中 p 为正常数. p的几何意义是:焦点坐标是准线方程为:焦点到准线的距离对“标准”的理解 一般地,把顶点在原点、焦点F在坐标轴上的抛物线的方程叫做抛物线的标准方程.
MxMl向右
向左
向上
向下
yx例题1、(1)已知抛物线的标准方程是 y 2 = 6 x ,求它的焦点坐标及准线方程(2)已知抛物线的焦点坐标是 F(0,-2),求抛物线的标准方程x 2 =-8 y图象小结数形结合的思想。题后反思:小结生活中的抛物线---喷泉生活中的抛物线---赵州桥卫星天线生活中的抛物线例2:一种卫星接收天线的轴截面如下图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处。已知接收天线的径口(直径)为4.8m,深度为0.5m。建立适当的坐标系,求抛物线的标准方程和焦点坐标。小结解:如上图,在接收天线的轴截面所在平面内建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合。 即
所以,所求抛物线的标准方程是 ,焦点的坐标是小结:1、抛物线的定义和四种标准方程的形式2、抛物线的标准方程与图象之间的特征关系3、数形结合的思想方法o返回解:(2)因为焦点在 y 轴的负半轴上,并且 = 2,p = 4 ,所以所求抛物线的标准方程是 x2 =-8y .
yoFN··x方案:以l为y轴,过点F且垂直于l的直线为x轴
建立直角坐标系,则点F(p ,0).设动点M(x,y),由抛物线定义得M(x,y)方案3比较方案:以定点F为原点,过点F且垂直于l的直线为x轴建立直角坐标系.yKFMN··x设动点M(x,y),由抛物线定义得则点F(0 ,0), l 的方程为x= -- p .l比较方案1比较l方案:以过F且垂直于 l 的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xoy.M(x,y)F两边平方,整理得这就是所求的轨迹方程.N依题意得方案1方案2三种建系方案比较标准方程
