五章三角形学案

5.1认识三角形(1)
学习目标
1、经历小木棒拼摆三角形的实践活动，探索三角形三边之间的关系；
2、懂得判断三条线段能否构成一个三角形的方法，并能用于解决有关问题；
3、帮助学生树立数学源于客观实际，用于实际的观念，激发学生学习兴趣。
学习过程
一、创设情境，引入新课
1、欣赏三角形图片(塔吊、自行车、天安门及胜利油田等图片)。在日常生活生活中你见到什么物体上有三角形？
2．观察图片中屋顶框架小组讨论
(1)能从中找出四个不同的三角形吗？(2)与你的同伴交流各自找到的三角形。 (3)这些三角形有什么共同特点？
3．归纳三角形特点得到定义： 。
4．怎样表示三角形？找出图片中的三角形,并用符号分别表示出来。
5．认识三角形的基本要素(边，角，顶点)及其表示方法。
二．探索新知，学习新课
1．做一做：选择3cm、5cm、7cm、10cm的小棒摆一摆，三根一组共有四种组合,其中哪些组合不能组成三角形？哪些组合能构成三角形？
(1)取出其中5，7，10厘米的小木棒，你能摆成三角形吗？
(2)取出其中3，5，10厘米的小木棒，结果呢？
2．议一议：
元宵节的晚上，房梁上亮起了彩灯，装有黄色彩灯的电线与装有红色彩灯的电线哪根长呢？说明你的理由。（136页） 由此，你得到的结论是： .
3．分别量出下面三个三角形的三边长度, 并填入空格内:
(图1) (图2) (图3)
图1：a = ________, b = ________, c = ________,
图2：a = ________, b = ________, c = ________,
图3：a = ________, b = ________, c = ________,
计算每个三角形的任意两边之差，并与第三边比较，你得到的结论是： .
三．例题及练习讲解
1. 用下面三根小木棒的长度能摆成三角形吗 为什么 和同伴交流。
(1)7cm，5cm，10cm (2)3cm，5cm，10cm (3)10cm，3cm，7cm
2. 等腰三角形一边长9cm，另一边长4cm，它的第三边是多少？为什么？
3．若三角形的两边分别为2和7，第三边为偶数，求第三边的长．
四．当堂检测：
1．两根木棒的长分别为7cm和10cm，要选择第三根木棒，将它们钉成一个三角形框架，那么第三根木棒长x（cm）的范围是（ ）．
A．x<17 B．x>3 C．02．如图1所示，∠BAC的对边是（ ）．
A．BD B．DC C．BC D．AD
( http: / / )
(1) (2)
3．四根铁棒的长分别为4cm，6cm，10cm，15cm以其中三根的长为边长，焊接成一个三角形框架，则这个框架的周长可能是（ ）．
A．31cm B．29cm C．25cm D．20cm
4．如图2所示，
（1）图中共有______个三角形；（2）△ABE的顶点是_____，三个内角是________；
（3）∠B是哪些三角形的内角；_____________________；
(4）AC是哪些三角形的边：_________________；
（5）∠B是△ABC，△DBC中________，_______边的对角；
（6）AC分别是△AOC，△ADC，△AEC，△ABC中∠______，∠______，∠______，∠______的对边．
5．三角形两边长为6cm和8cm，那么周长C的范围是什么？
6．一个三角形的三边长分别是5，10，a-2，则a的取值范围是_______．
五．小结：通过本节课的学习，你得到的收获是哪些？
六．作业
： 习题5.1 1，2
教学反思：
学生能从生活中抽象出几何图形 ,感受到我们生活在几何图形的世界之中.；在验证三边和差时充分的调动了学生的积极性，在实践中总结了结论,学生印象深刻。通过观察、操作、想象、推理、交流等活动,发展了学生的空间观念,推理能力和有条理地语言表达能力，课堂检测效果较好。
5.2 认识三角形（2）
学习目标
1．通过观察、想象、推理、交流等活动，发展推理能力和有条理地表达能力；毛
2．能证明出“三角形内角和等于180°”，能发现“直角三角形的两个锐角互余”；
3、按角将三角形分成三类。
课前准备：预先剪好两个三角形，一副三角板。
学习过程：
一、复习巩固：
1、填空：
（1）当0°＜＜90°时，是 角；
（2）当＝ °时，是直角；
（3）当90°＜＜180°时，是 角；
（4）当＝ °时，是平角。
2、如右图，
∵AB∥CE，（已知）
∴∠A＝ ，（ ）
∴∠B＝ ，（ ） （第2题）
二、探索新知：
根据自己手中的一副特殊的三角板，知道三角形的三个内角和等于 ，那么是否对其他的三角形也有这样的一个结论呢？
用自己剪好的一个三角形，把三个角撕下来，拼在一块。你发现了什么？小组交流。
你得到的结论是 。
练习1：
1、判断：
（1）一个三角形的三个内角可以都小于60°； （ ）
（2）一个三角形最多只能有一个内角是钝角或直角； （ ）
2、在△ABC中，
（1）∠C=70°，∠A=50°，则∠B= 度；
（2）∠B=100°，∠A=∠C，则∠C= 度；
（3）2∠A=∠B+∠C，则∠A= 度。
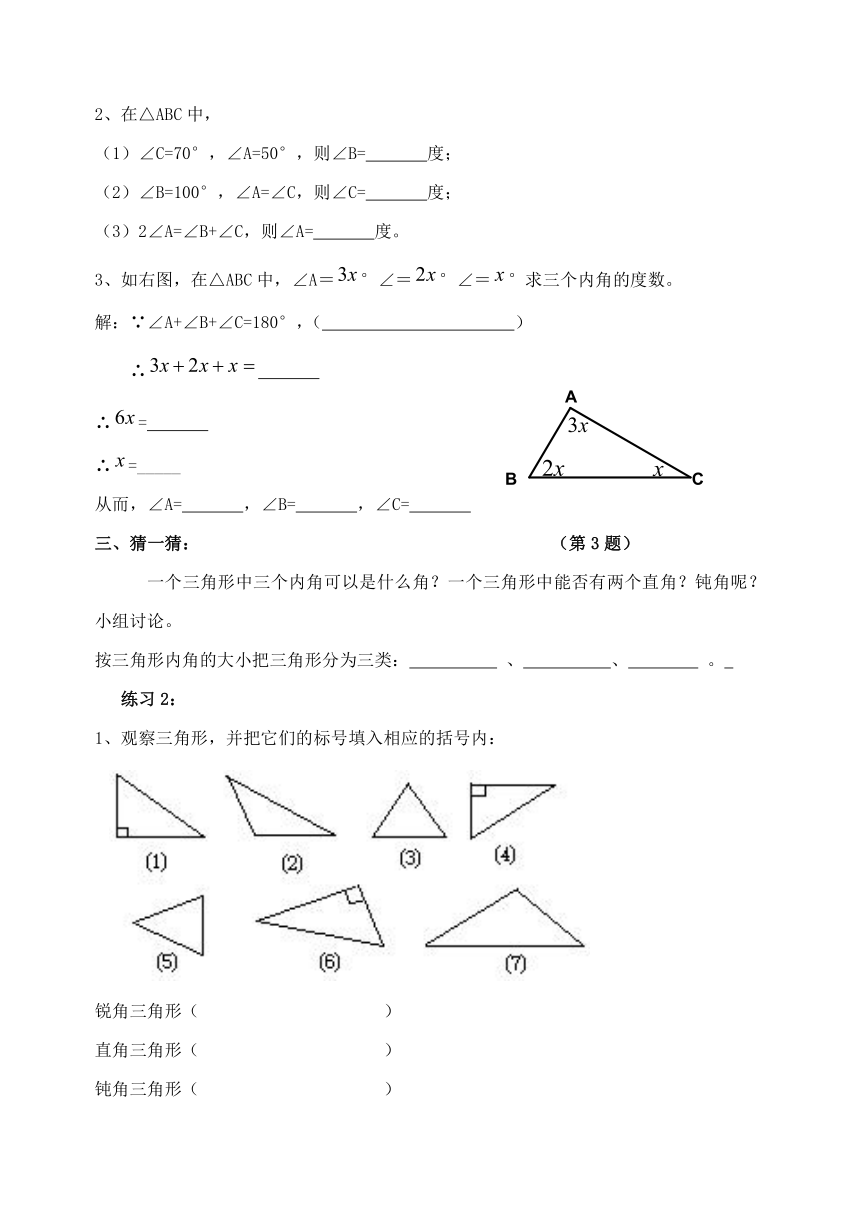
3、如右图，在△ABC中，∠A＝°∠＝°∠＝°求三个内角的度数。
解：∵∠A+∠B+∠C=180°，（ ）
∴
∴=
∴=_____
从而，∠A= ，∠B= ，∠C=
三、猜一猜： （第3题）
一个三角形中三个内角可以是什么角？一个三角形中能否有两个直角？钝角呢？小组讨论。
按三角形内角的大小把三角形分为三类： 、 、 。
练习2：
1、观察三角形，并把它们的标号填入相应的括号内：
锐角三角形（ ）
直角三角形（ ）
钝角三角形（ ）
2、一个三角形两个内角的度数分别如下，这个三角形是什么三角形？
（1）30°和60° （ ）
（2）40°和70° （ ）
（3）50°和30° （ ）
（4）45°和45° （ ）
四、猜想结论：
思考：直角三角形中的两个锐角有什么关系？
结论： 。
练习3：
1、 观察下列的直角三角形，分别写出它们符号表示、直角边和斜边。
（图1） （图2）
(1)图1中的直角三角形用符号写成 ，直角边是 和 ，斜边是 ；
(2)图2中的直角三角形用符号写成 ，直角边是 和 ，斜边是 ；
2、如下图，在 Rt△CDE,∠C和∠E的关系是 ，其中∠C=55°，则∠E=
3、如上图， 在Rt△ABC中，∠A=2∠B，则∠A= 度，∠B= 度；
五．当堂检测：
1、选择：三角形三个内角中，锐角最多可以是（ ）
A、0个 B、1个 C、2个
2、如下图，△ABC中，∠A=60°，∠C=80°，∠B= 度；
第2题 第3题
3、如上图，∠1=60°，∠D=20°，则∠A= 度；
4、如右图，AD⊥BC，∠1=40°，∠2=30°，
则∠B= 度，∠C= 度
5、在空白处填入“锐角”、“直角”或“钝角”：
(1)如果三角形的三个内角都相等，那么这个三角形
是 三角形； 第4题
(2)如果三角形的两个内角都小于40°，那么这个三角形是 三角形。
提高练习：
1.已知△ABC中，∠A∶∠B∶∠C=1∶3∶5，求∠A、∠B和∠C的度数，它是什么三角形？
2、如右图，已知△ABC中，∠1=27°，∠2=85°，
∠3=38°求∠4的度数
3、一个零件的形状如图所示，按规定∠A应该等于90°，∠B、∠D应分别是20°和30°，李叔叔量得∠BCD=142°，就断定这个零件不合格，你能说出其中的理由吗？
作业：课本习题5.2：3，4。
教学后记：学生剪、拼得到三角形内角和为180°，再请学生用所学知识推导出来，使学生的感性认识和理性认识都得到提高，用“三角形三个内角和等于180°”计算一些简单角度，能对三角形按内角的大小进行分类并判断三角形是什么三角形，也知道直角三角形的两锐角互余，但不能灵活运用。
5.1认识三角形（3）
学习目标：1、通过观察、想象、推理、交流等活动，发展空间观念、推理能力和有条理地表达能力；
2、了解角平分线和三角形的中线的概念，并会在三角形中画出角平分线和中线。
课前准备：任意一个三角形和锐角三角形、钝角三角形和直角三角形各一个。
学习过程：
1、 探索新知：
1、 任意画一个三角形，设法画出它的一个内角的平分线。
1、 你能通过折纸的方法得到它吗？
得到结论：
三角形 叫做三角形中这个角的角平分线。简称三角形的角平分线。
规范书写：
如图：∵AD是三角形ABC的角平分线。
∴∠1＝∠2＝_____∠BAC
或：∠BAC＝ 2∠1＝ 2∠2
问题：三角形有几条角平分线？三角形的三条角平分线有怎样的位置关系？
动手操作：请你画出△ABC（锐角三角形）的所有角平分线，并且观察这些角平分线有什么规律？对于钝角三角形呢 直角三角形呢 它们的角平分线也有这样的规律吗
得到结论：
一个三角形共有三条角平分线，它们都在三角形 部，而且相交于 点。
活动二：1、任意画一个三角形，设法画出它的三条中线，它们有怎样的位置关系？小组交流。
2、你能通过折纸的方法得到它吗？
得到结论：
连结三角形 叫做三角形这个边上的中线。简称三角形的中线。
规范书写：
如图：∵AD是三角形ABC的中线。
∴BD＝DC＝BC
或：BC＝ 2BD＝2DC
问题：三角形有几条中线？三角形的三条中线有怎样的位置关系？
动手操作：请你画出△ABC（锐角三角形）的所有中线，并且观察这些中线有什么规律？对于钝角三角形呢 直角三角形呢 它们的中线也有这样的规律吗
得到结论：
一个三角形共有三条中线，它们都在三角形 部，而且相交于 点。
二、巩固练习：
1. 如图,已知,AD是BC边上的中线,AB=5cm,AD=4cm, △ABD
的周长是12cm,求BC的长.
2.△ABC中,∠B=80°∠C=40°,BO、CO平分∠B、∠C，则∠BOC=______.
三、课堂测试：
1、AD是△ABC的角平分线（D在BC所在直线上），那么∠BAD=_______=______.
AE是△ABC的中线（E在BC所在直线上），那么BE=___________=_______BC.
2、如图,在△ABC中,∠BAC=60°,∠B=45°,AD是△ABC的一条角平分线求 ∠ADB的度数.
作 业： 课本习题5.3：1、2。
教学后记：学生基本上能明白三角形的角平分线、中线的定义，但是在较复杂一点的题目中也会出现以下错误：
（1） 如右图，已知AD是三角形ABC的角平分线，则∠B=∠C；
（2） 有部分生会把三角形的角平分线和三角形的中线混淆。
如：AD是三角形ABC的角平分线，则BD=CD。
对角平分线、三角形的中线的运用有待真正的提高。
5.1 认识三角形（4）
学习目标：1、通过观察、想象、推理、交流等活动，发展空间观念、推理能力和有条理地表达能力；
2、了解三角形的高，并能在具体的三角形中作出它们。
课前准备：学生预先剪好三种三角形，一副三角板。
学习过程：
一、引出新课：
过三角形的一个顶点A，你能画出它的对边BC的垂线吗？试试看，你准行！
二、探索新知：
1、三角形的高： 叫做三角形的高线，简称三角形的高。
规范书写：
如图，线段AM是BC边上的高。
∵ AM是BC边上的高
∴AM⊥BC
2、做一做：每人准备一个锐角三角形纸片
（1）你能画出这个三角形的高吗？
你能用折纸的方法得到它吗？
（2）这三条高之间有怎样的位置关系呢？
小组讨论交流。
结论：锐角三角形的三条高在三角形的 部且交于 点。
3、议一议：
每人画出一个直角三角形和一个钝角三角形
（1）画出直角三角形的三条高，并观察它 们有怎样的位置关系？
（2）你能折出钝角三角形的三条高吗？
你能画出它们吗？
（3）钝角三角形的三条高交于一点吗？
它们所在的直线 交于一点吗？
小组讨论交流
结论：
1、直角三角形的三条高交于 。
2、钝角三角形的三条高所在直线交于一点，此点在三角形的 部。
三、巩固练习：
如图，（1）共有 个直角三角形
（2）高AD、BE、CF相对应的底分别是 、 。
（3）AD=3、BC=6、AB=5、BE=4，
则S△ABC= 、CF= 、
AC= 。
四、课堂测试：
1．三角形三边上的高的交点恰是三角形的一个顶点，则这个三角形是（ ）．
A．锐角三角形 B．直角三角形 C．钝角三角形 D．以上三种都不是
2．钝角三角形的高在三角形外的条数是_________条．
3．如图，按要求画图并填写字母；
（1）画出△ABD中AB边上的高，它是________；
（2）画出△ABC中AB边上的高，它是________；
（3）画出△ABC中AC边上的高，它是________；
（4）画出△ABD中AD边上的高，它是________；
（5）画出△ADC中AD边上的高，它是________．
4．如图2，AC⊥BC，CD⊥AB，DE⊥BC，分别交BC，AB，BC于
C，D，E．下列说法中， 不正确的是（ ）．
A．AC是△ABC的高 B．DE是△BCD的高
C．DE是△ABE的高 D．AD是△ACD的高
教学反思：锐角三角形和直角三角形的高掌握得较好。
钝角三角形的高，特别是钝角边上的两条高较差。
5、2图形的全等
学习目标：借助具体情境和图案，经历观察、发现和实践操作重叠图形等过程，了解图形全等的意义，了解全等图形的特征。
课前准备：把课本当中的图画在白纸上，带好剪刀和复写纸
学习过程：
1、 看一看
1．引导学生观察课本两组图形。
2．多举一些比较熟悉的能全等或不全等图形的实例，想象全等图形与不全等图形的区别。例如：
（1） 同一张底片冲印出两张相同尺寸的相片与两张不同尺寸的相片。
（1） 同一人的两只手掌与一大人左手掌和一小孩的左手掌。
（1） 一个三角形和一个四边形
3．通过观察，说出下面两组图形中上、下两个图形的异同之处，与同学交流你的看法。
（1）
（2）
1、 做一做
1.用复写纸印出任一封闭图形。
2.把两张纸叠在一起，用剪子随意剪出一个图形。
1、 议一议
1.从“做一做”中得到的两个图形有什么特征？
2.在看一看中，你的看法如何？
3. 称为全等图形。
全等图形的 和 都相同
四、做一做
按课本做一做的要求进行实践活动。（注意：把划分出的两个图形叠在一起应重合，通过数小正方形个数可知划分出的图形中应含有6个小正方形。
五、课堂测试
1．如图所示，A，B，C，D，E，F几个区域中，其中全等图形的对数为（ ）．
A．1 B．2 C．3 D．4
2．下列说法正确的是（ ）．
A．周长相等的长边形是全等形;
B．所有的五角星都是全等形;
C．面积相等的三角形是全等形;
D．周长相等的正方形是全等形
3．如果△ABC与△DE是全等形，则有（ ）．
（1）它们的周长相等；（2）它们的面积相等；
（3）它们的每个对应角都相等；（4）它们的每条对应边都相等．
A．（1）（2）（3）（4） B．（1）（2）（3） C．（1）（2） D．（1）
4．指出下列图形中的全等图形．
( http: / / / )
教后记：
本节课从熟悉的几何图形，、实物图形入手，让学生对图形全等有一个感性的认识，调动学生的积极性，很快抓住学生的注意力，激起学生的探索欲，学生的掌握情况较好，对于全等图形的理解较准确，但在分图形的过程中却遇到了一些困难。应加强这方面的练习。
5.3全等三角形
学习目标：掌握全等三角形对应边相等、对应角相等的性质，并能进行简单的推理计算。知识准备：
(1) 一个三角形共有______个顶点,_________个角,_______条边.
(1) 已知△ABC,它的顶点是_________,它的角是__________, 它的边是___________
(1) 两个图形完全重合指的是它们的形状___________,大小___________.
(1) 完全重合的两条线段_________(填 “相等”或 “不相等”)
完全重合的两个角_________(填 “相等”或 “不相等”)
学习过程：
1、 实验活动
找出图画中全等的图形：（见课本）从而归纳全等三角形的定义及性质
1．全等三角形的定义及有关概念和性质．
(1)定义： (2)反例：举出不全等的三角形的例子．
请同学们观察周围有没有能完全重合的两个平面图形？
(3)对应元素及性质： 叫对应顶点、 叫对应边、 叫对应角，观察全等三角形中对应元素的关系，发现对应边 ，对应角 ．
2．学习全等三角形的符号表示及读法和写法．
自学“≌”的含义和读法，并注意对应顶点写在对应位置上．
举例说明： 如图，∵ △ABC≌DFE，(已知)
∴AB=DF，AC=DE，BC=FE，(全等三角形的对应边相等)
∠A=∠D，∠B=∠F，∠C=∠E．(全等三角形的对应角相等)
1、 总结寻找全等三角形对应元素的方法，渗透全等变换的思想
(1) 全等用符号_________表示.读作__________.
(2) 三角形ABC全等于三角形DEF,用式子表示为______________
(3) 已知△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′∠C=∠C′;
AB=A′B′,BC=B′C′,AC=A′C′.则△ABC_______△A′B′C′.
(4) 如右图△ABC≌△BCD,∠A的对应角是∠D,∠B的对应角∠E,则
∠C与____是对应角;AB与_____是对应边, BC与_____是对应边,
AC与____是对应边.
（5）判断题:
①全等三角形的对应边相等,对应角相等.( )
②全等三角形的周长相等.( )
③面积相等的三角形是全等三角形.( )
④全等三角形的面积相等.( )
三、课堂测试：
1．下列说法正确的是（ ）．
A．全等三角形是指形状相同的三角形 B．全等三角形是指面积相等的两个三角形
C．全等三角形的周长和面积相等 D．所有等边三角形是全等三角形
2．如图1所示，△ABC≌△AEF，AC与AF是对应边，那么∠EAC等于（ ）．
A．∠ACB B．∠CAF C．∠BAF D．∠BAC
(1) (2) (3) (4)
3．如图2，△ABC≌△CDA，并且AB=CD，那么下列结论错误的是（ ）．
A．∠1=∠2 B．AC=CA C．∠D=∠B D．AC=BC
4．如图3，△ABC≌△ADE，∠B与∠D是对应角，AB与 ( http: / / / )AD是对应边，另外两组对应边为________，对应角为_____________．
5．如图4，如果△ABC≌△A′B′C′，那么
∠A=________，∠ABC=________，∠C=_________，
AB=_________，BC=_________，AC∥________．
四、作业： 课本习题5.7：1、2。
教学后记：
学生对全等三角形的全等还是理解得比较好的。而在找全等三角形的对应边、对应角的时候，简单的并且放的位置比较好时，才容易找到。而稍为旋转的图形中找起来就要花些时间。应用性质计算、证明有一些困难。
5.4.1探索三角形全等的条件（1）
学习目标：1、经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程；
2、掌握三角形的“边边边”条件，了解三角形的稳定性。
3、在探索三角形全等条件及其运用的过程中，能够进行有条理的思考并进行简单的推理。
知识准备：
1、全等三角形的 相等， 相等。
2、如图1，已知△AOC≌△BOD，则∠A=∠B，∠C= ， =∠2，对应边有AC= ， =OB， =OD。
3、如图2，已知△AOC≌△DOB，则∠A=∠D，∠C= ， =∠2，对应边有AC= ，OC= ，AO= 。
4、如图3，已知∠B=∠D，∠1=∠2，∠3=∠4， AB=CD，AD=CB，AC=CA。则△ ≌ △
5、判定两个三角形全等，依定义必须满足（ ）
（A）三边对应相等 （B）三角对应相等
（C）三边对应相等和三角对应相等 （D）不能确定
学习过程：
1、 实验操作
1、 画出一个三角形，使它的三个内角分别为40°，60°，80°，把你画的三角形与小组内画的进行比较，它们一定全等吗？
结论：
2、画出一个三角形，使它的三边长分别为3cm 4cm 7cm ,把你画的三角形与小组内画的进行比较，它们一定全等吗？
结论：
1、 巩固练习：
1、 下列三角形全等的是
2、三边对应相等的两个三角形例全等，简写为 或
3、如图，AB=AC， BD=DC 4、如图，AM=AN， BM=BN
求证：△ABD≌△ACD 求证：△AMB≌△ANB
证明：在△ABD和△ACD中 证明：在△AMB和△ANB中
∴ △ABD △ACD（ ） ∴ ≌ （ ）
5、如图，AD=CB，AB=CD 6、如图，PA=PB，PC是△PAB的
中线，∠A=55°
求证：∠B=∠D 求：∠B的度数
证明：在 中 解：∵PC是AB边上的中线，
∴AC= （中线的定义）
在 中
∴ △ ≌△ （ ） ∴ ≌ （ ）
∴∠B=∠D（全等三角形对应角相等）
∴∠A=∠B（ ）
∵ ∠A=55°（已知）
∴ ∠B=∠A=55°（等量代换）
三、课堂测试：
1、 如图，AB=DC，BF=CE，AE=DF，你能找到一对全等的三角形吗？ 说明你的理由。
1、 如图，A、C、F、D在同一直线上，AF=DC，AB=DE，BC=EF
你能找到哪两个三角形全等？说明你的理由。
3、如图，已知AC=AD，BC=BD，CE=DE，则全等三角形共有 对，
并说明全等的理由。
教学反思：
本节课教学内容比较丰富，经历知识的发现过程中，培养了学生分类、探究、合作、归纳的能力。具体操作时间相对比较紧张，对教学环节恰当的调控可以有效的完成本节课的教学目标，
5.4．2探索三角形全等的条件（2）
学习目标：1、经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程；
2、掌握三角形的“角边角”“角角边”条件，了解三角形的稳定性。
3、在探索三角形全等条件及其运用的过程中，能够进行有条理的思考并进行简单的推理。
知识准备：
1、三边对应相等的两个三角形全等，简写为 或
2、如图1，在△ABC中，AB＝AC，AD是BC边上的中线，AD能平分∠BAC吗？你能说明理由吗？
解：AD平分∠BAC。
∵AD是BC边上的中线（已知）
∴ ＝ （中线的定义）
在 中
EMBED Equation.3 （图 1）
∴ ≌ （ ）
∴∠BAD＝∠CAD（ ）
∴AD平分∠BAC（ ）
3、如图2， （图2）
（1）∵AC∥BD（已知）
∴∠ ＝∠ （ ）
（2）∵AD∥BC（已知）
∴∠ ＝∠ （ ）
4、如图3，
∵EA⊥AD，FD⊥AD（已知） （图3）
∴∠ ＝∠ ＝90°（ ）
学习过程：
1、 探索练习：
1、如果“两角及一边”条件中的边是两角所夹的边，比如三角形的两个内角分别是60°和80°，它们所夹的边为2cm，你能画出这个三角形吗？你画的三角形与同伴画的一定全等吗？
结论：
2、如果“两角及一边”条件中的边是其中一角的对边，比如三角形两个内角分别是60°和45°，一条边长为3cm。你画的三角形与同伴画的一定全等吗？
结论：
1、 巩固练习：
1、两角和它们的夹边对应相等的两个三角形全等，简写成 或
2、两角和其中一角的对边对应相等的两个三角形全等，简写成 或
3、如图，AB＝AC，∠B＝∠C，你能证明△ABD≌△ACE吗？
证明： △ABD和△ACE中
∴ ≌ （ ）
4、如图，已知AC与BD交于点O，AD∥BC，且AD＝BC，你能说明BO=DO吗？
证明：∵AD∥BC（已知）
∴∠A= ，（ ）
∠D= ，（ ）
在 中，
∴ ≌ （ ）
∴BO=DO（ ）
5、如图，∠B＝∠C ，AD平分∠BAC，你能证明△ABD≌△ACD？
若BD＝3cm，则CD有多长？
证明：∵AD平分∠BAC（ ）
∴∠ ＝∠ （角平分线的定义）
在△ABD和△ACD中
∴△ABD △ACD（ ）
∴BD＝CD（ ）
∵BD＝3cm（已知）
∴CD＝ ＝ （等量代换）
6、如图，在△ABC中，BE⊥AD于E，CF⊥AD于F，且BE＝CF，那么BD与DC相等吗？你能说明理由吗？
解：BD＝DC。
∵BE⊥AD于E，CF⊥AD于F
∴∠ ＝∠ ＝90°（垂直的定义）
在 中，
∴ ≌ （ ）
∴BD＝DC（ ） （第6题）
7、如图，已知AB＝CD，∠B＝∠C，你能说明△ABO≌△DCO吗？
1、 课堂测试：
1、如图，AB∥CD，∠A＝∠D，BF＝CE，∠AEB＝110°，求∠DCF的度数。
2、如图，在Rt△ACB中，∠C＝90°，BE是角平分线，ED⊥AB于D，
且BD＝AD，试确定∠A的度数。
教学后记：在探究活动中，实践、探究、交流，充分发挥学生的想象力和集体的智慧，使不同的学生有不同的发展，从复习旧知入手，让学生对三角形全等的条件有一个感性的认识，调动学生的积极性，很快抓住学生的注意力，激起学生的探索欲，为实践活动做好充分的铺垫。
5.4.3探索三角形全等的条件（3）
学习目标：使学生掌握并初步学会应用三角形全等的判定Ⅰ——边角边公理
学习过程：
一、知识回顾
判断三角形全等的方法有几种，分别用语言加以描述。
1、 探索新知：
1、通过小组讨论，明确两边及一角的情况，就此三个条件找出分为两类，并对每类的情况进行解释说明。
2、画图比较
（1）．按要求画图：已知两边分别为2．5厘米、3．5厘米，它们的夹角为
４０°。分小组画图，要求画出的三角形尽可能准确，减少误差。
（2）．按要求作图：以２．５厘米，３．５厘米为边，以２．５厘米的边所对的角为４０°。分小组画图，要求同１。
3、合作学习
（1） 学生根据各小组所画的图形，剪下后对比分析，看图形是否完全重合。
（2） 通过对比、交流，最终对研究的问题作出决策。
（3） 总结结论。并互相补充产生这种情况的原因。
四、 练习提高
1．分别找出各题中的全等三角形，说明理由。
2．小明做了一个如图所示的风筝，其中∠EDH=∠FDH，DE=FD。将上述条件标注在图中，小明不用测量就能知道EH=FH吗？与同伴交流。
SHAPE \* MERGEFORMAT
第2题 第3题
3．在△ABC中，AB=AC，AD是∠BAC的角平分线。那么BD与CD相等吗？为什么？
4．如图，已知AB＝AC，AD＝AE。那么∠B与∠C相等吗？为什么？
5．如图，∠B＝∠E，AB＝EF，BD＝EC，那么△ABC与　△FED全等吗？为什么？
AC∥FD吗？为什么？
课堂测试：
1．已知：如图，AB＝AC，F、E分别是AB、AC的中点．
求证：△ABE≌△ACF．
2．已知：点A、F、E、C在同一条直线上， AF＝CE，BE∥DF，BE＝DF．
求证：△ABE≌△CDF．
教后记：
通过小组合作画图的过程，为学生提供展示自己聪明才智的机会，并且在此过程中更利于教师发现学生分析问题解决问题的独到见解，以及思维的误区，以便指导今后的教学。
从本节课开始，学生要逐步学习几何命题的证明，正式进入逻辑推理的系统训练阶段，也是学生学习推理的入门阶段，因此，要把增强学生学习几何的兴趣和信心，作为本课的首要任务．
5.5作三角形
学习目标：1、在分别给出的两角夹边、两边夹角和三边的条件下，能够利用尺规作三角形。
2、能结合三角形全等的条件与同伴交流作图过程和结果的合理性。
学习过程：
一.知识准备：
（1）已知线段a，求作线段AB，使得AB=a。
(2) 已知：∠
求作：∠AOB，使∠AOB=∠
(3) 已知：M为∠AOB边上的一点，如图所示，过M作直线CD，使得CD//OA。
二.三角形与已知三角形全等
1、已知三角形的两边及其夹角,求作这个三角形.
已知：线段a，c，∠α。
求作：ΔABC，使得BC= a，AB=c，∠ABC=∠α。
2、已知三角形的两角及其夹边,求作这个三角形.
已知：线段∠α，∠β，线段c 。
求作：ΔABC，使得∠A=∠α，∠B=∠β，AB=c。
作法：（1）作____________=∠α;
(2) 在射线______上截取线段_________=c;
(3) 以______为顶点,以_________为一边,
作∠______=∠β,________交_______于
点_______.ΔABC就是所求作的三角形.
3、已知三角形的三边,求作这个三角形.
已知：线段a，b，c。
求作：ΔABC，使得AB=c，AC=b，BC=a。
二、课堂检试
1．利用尺规作图不能唯一作出三角形的是（ ）．
A．已知三边 B．已知两边及其夹角
C．已知两角及其夹边 D．已知两边及其中一边的对角
2．用尺规作图，已知三边作三角形，用到的基本作图是（ ）．
A．作一个角等于已知角 B．作已知直线的垂线
C．作一条线段等于已知线段 D．作角的平分线
3．如图，使用直尺作图，看图填空：
(1) (2) (3) (4)
（1）过点_______和_______作直线AB；
（2）连接线段______；
（3）以点_______为端点，过点______作射线_______．
（4）延长线段________到_______，使BC=2AB．
4．如图所示，已知∠α和线段a，用尺规作一个三角形，使其一个内角等于∠α，夹这个角的两边分别为2a和a．
5．如图，已知线段a，用尺规作△ABC，使AB=a，BC=AC=2a．
教学后记：本节课的内容比较多，学生对作图的步骤有混淆的情况发生，学生对于自己探索“已知三角形三边作三角形”的作图过程存在一定的难度。
用自己的语言表达作图过程也是不大理想。有待练习巩固。
5.6利用三角形全等测距离
学习目标：1、能利用三角形的全等解决实际问题，体会数学于实际生活的联系；
2、能在解决问题的过程中进行有条理的思考和表达。
知识准备：
1、三边对应相等的两个三角形全等，简写为 或
2、两角和它们的夹边对应相等的两个三角形全等，简写成 或
3、两角和其中一角的对边对应相等的两个三角形全等，简写成 或
4、两边和它们的夹角对应相等的两个三角形全等，简写成 或
5、全等三角形的性质：两三角形全等，对应边 ，对应角
6、如图；△ADC≌△CBA，那么，
7、如图；△ABD≌△ACE，那么，
学习过程：
一、探索练习：
如图：A、B两点分别位于一个池塘的两端，小明想用绳子测量A，B间的距离，但绳子不够长。他叔叔帮他出了一个这样的主意：
先在地上取一个可以直接到达A点和B点的点C，连接AC并延长到E，使CD=AC；连接BC并延长到E，使CE=CB；连接DE并测量出它的长度；
（1） DE=AB吗？请说明理由
（1） 如果DE的长度是8m，则AB的长度是多少？
二、巩固练习：
1． 如图，山脚下有A、B两点，要测出A、B两点的距离。
（1） 在地上取一个可以直接到达A、B点的点O，连接AO并延长到C，使AO=CO，你能完成下面的图形？
（2） 说明你是如何求AB的距离。
2．如图，要量河两岸相对两点A、B的距离，可以在AB的垂线BF上取两点C、D，使CD=BC，再定出BF的垂线DF，使A、C、E在一条直线上，这时测得DE的长就是AB的长，试说明理由。
3．如图，A，B两点分别位于一个池塘的两端，完成下图并求出A、B的距离
三、课堂测试：
1．在一座楼相邻两面墙的外部有两点A、C，如图所示，请设计方案测量A、C两点间的距离。
2．如图，一池塘的边缘有A、B两点，试设计两种方案测量A、B两点间的距离
教学后记：大部分学生能利用三角形的全等解决实际问题，但对解决问题的过程中进行有条理的思考和表达较薄弱。
5.7探索直角三角形全等的条件
学习目标：1、经历探索直角三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程；
2、掌握直角三角形全等的条件，并能运用其解决一些实际问题。
3、在探索直角三角形全等条件及其运用的过程中，能够进行有条理的思考并进行简单的推理。
知识准备：
1、判定两个三角形全等的方法： 、 、 、
2、如图，Rt△ABC中，直角边是 、 ，
斜边是
3、如图，AB⊥BE于C，DE⊥BE于E，
（1）若∠A=∠D，AB=DE，
则△ABC与△DEF （填“全等”或“不全等” ）
根据 （用简写法）
（2）若∠A=∠D，BC=EF，
则△ABC与△DEF （填“全等”或“不全等” ）
根据 （用简写法）
（3）若AB=DE，BC=EF，
则△ABC与△DEF （填“全等”或“不全等” ）
根据 （用简写法）
（4）若AB=DE，BC=EF，AC=DF
则△ABC与△DEF （填“全等”或“不全等” ）
根据 （用简写法）
二、学习过程：
（一）探索练习：（动手操作）：
已知线段a ，c (aAB=c ，CB= a
1、按步骤作图： a c
1 作∠MCN=∠=90°，
1 在射线 CM上截取线段CB=a，
③以B 为圆心，C为半径画弧，交射线CN于点A，
④连结AB
2、与同桌重叠比较，是否重合？
3、从中你发现了什么？
三、巩固练习：
1． 如图，△ABC中，AB=AC，AD是高，
则△ADB与△ADC （填“全等”或“不全等” ）
根据 （用简写法）
1． 如图，CE⊥AB，DF⊥AB，垂足分别为E、F，
（1）若AC//DB，且AC=DB，则△ACE≌△BDF，
根据
（2）若AC//DB，且AE=BF，则△ACE≌△BDF，
根据
（3）若AE=BF，且CE=DF，则△ACE≌△BDF，
根据
（4）若AC=BD，AE=BF，CE=DF。则△ACE≌△BDF，
根据
（5） 若AC=BD，CE=DF（或AE=BF），则△ACE≌△BDF，
根据
3、判断两个直角三角形全等的方法不正确的有（ ）
（A） 两条直角边对应相等 （B）斜边和一锐角对应相等
（C）斜边和一条直角边对应相等 （D）两个锐角对应相等
4、如图，B、E、F、C在同一直线上，AF⊥BC于F，DE⊥BC于E，
AB=DC，BE=CF，你认为AB平行于CD吗？说说你的理由
答：
理由：∵ AF⊥BC，DE⊥BC （已知）
∴ ∠AFB=∠DEC= °（垂直的定义）
在Rt△ 和Rt△ 中
∴ ≌ （ ）
∴∠ = ∠ （ ）
∴ （内错角相等，两直线平行）
5、如图，广场上有两根旗杆，已知太阳光线AB与DE是平行的，经过测量这两根旗杆在太阳光照射下的影子是一样长的，那么这两根旗杆高度相等吗？说说你的理由。
四、课堂测试：
1、判断题：
（1）一个锐角和这个锐角的对边对应相等的两个直角三角形全等。（ ）
（2）一个锐角和锐角相邻的一直角边对应相等的两个直角三角形全等（ ）
（3）一个锐角与一斜边对应相等的两个直角三角形全等（ ）
（4）两直角边对应相等的两个直角三角形全等（ ）
（5）两边对应相等的两个直角三角形全等（ ）
（6）两锐角对应相等的两个直角三角形全等（ ）
（7）一个锐角与一边对应相等的两个直角三角形全等（ ）
（8）一直角边和斜边上的高对应相等的两个直角三角形全等（ ）
2、如图，∠D=∠C=90°，请你再添加一个条件，使△ABD≌△BAC，并在
添加的条件后的（ ）内写出判定全等的依据。
（1） （ ）
（2） （ ）
（3） （ ）
（4） （ ）
3、如上图，AD⊥DB，BC⊥CA，AC、BD相交于点O，AC=BD，试说明AD=BC
4、如图，∠BAC=∠DCA=90°，AD=BC，∠1=20°，
你能求出∠D的度数吗？说说你的理由。
5、如图，AB//DC，AD//BC，AE⊥BD，CF⊥BD，垂足分别为E、F，
试说明AE=CF
教学反思：
利用教科书提供的素材和活动，鼓励学生经历画图、观察、比较、推理、交流的过程，在过程中逐步探索出最后的结论。在这个过程中，学生不仅得到了两个三角形全等的条件，同时体会了分析问题的一种方法，积累了数学活动经验。在教学时要及时调整方式，尽可能满足各层次多样化的学习需要，以认知水平、学习能力较好一些的学生带动稍微薄弱的学生的思维，但却不能代替他们的思考，掩盖他们的疑问。
D
C
B
A
F
D
E
40°
C
B
A
40°
C
D
B
A
H
E
F
D
A
C
E
D
B
F
E
D
A
B
C