利用三角形全等测距离

课件15张PPT。第六节
利用三角形全等测距离第六节
利用三角形全等测距离初 一 级 主 讲 人: 丘 明 剑1 、全等三角形具有什么性质？对应边相等，对应角相等。2 、证明两个三角形全等的条件有哪些？一、复习旧知识（1）“SSS”：三边对应相等的两个三角形全等.（2）“ASA”：两角和它们的夹边对应相等的两个三角 形全等.（3）“AAS”：两角和其中一角的对边对应相等的两个 三角形全等.
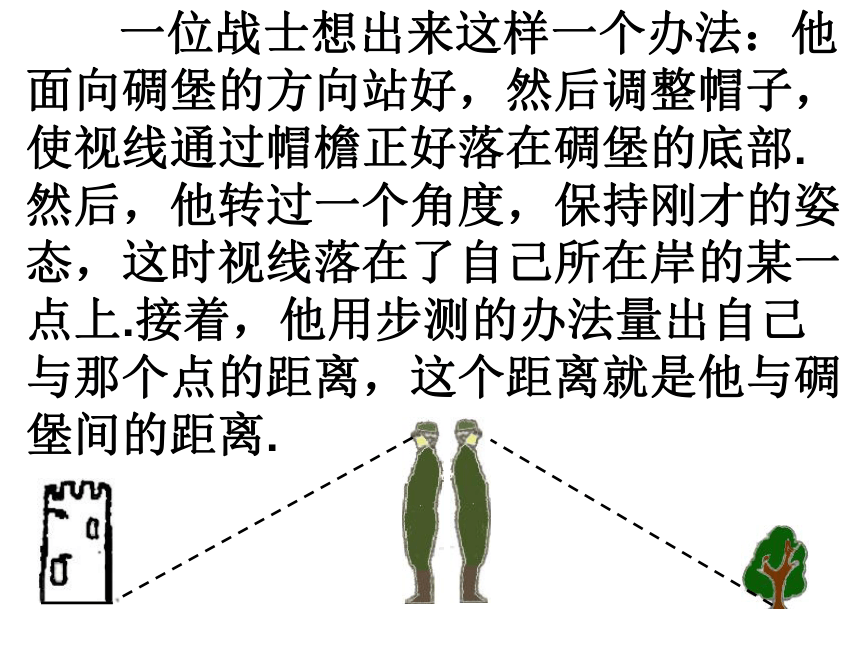
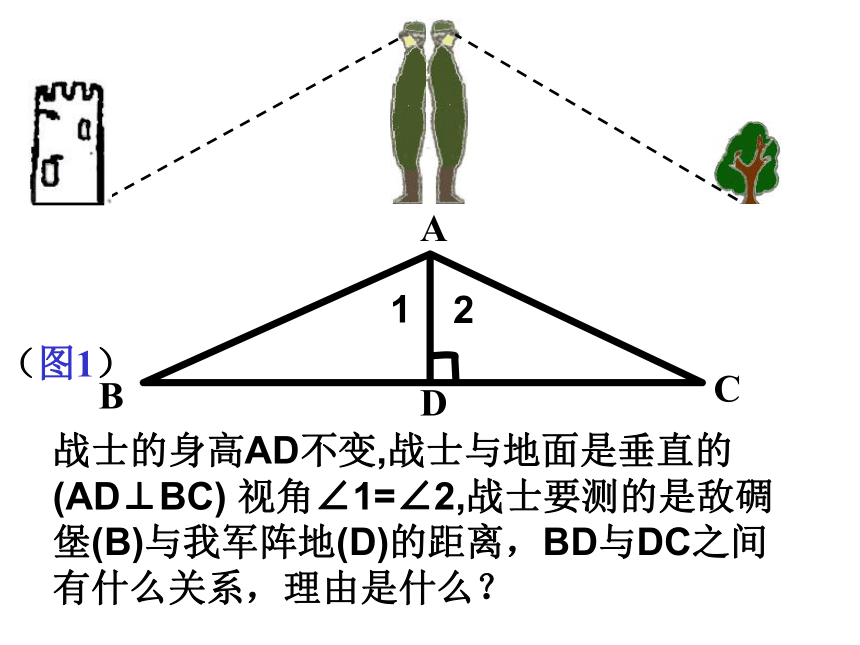
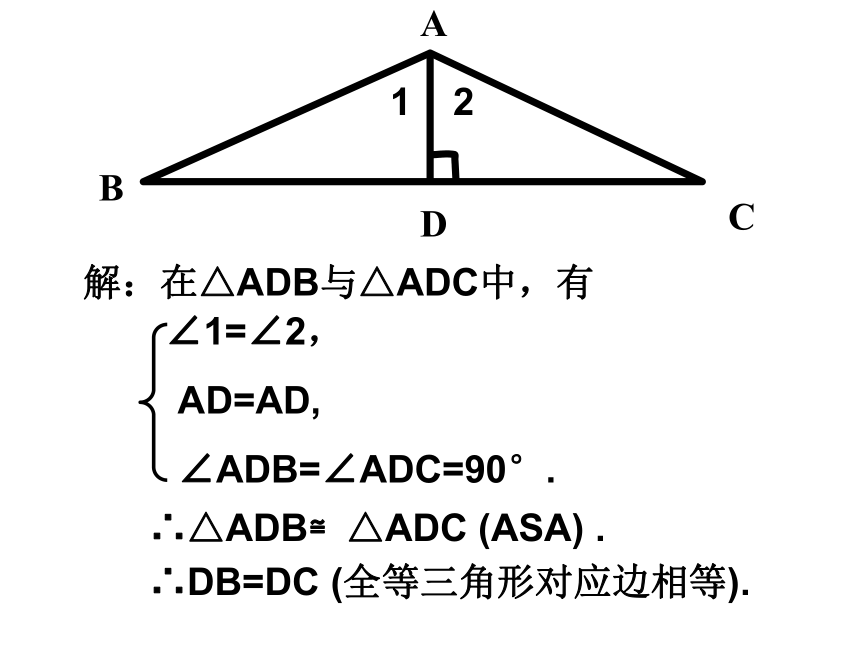
（4）“SAS”：两边和它们的夹角对应相等的两个三角形全等.下面是一位经历过战争的老人讲述的一个故事： 在一次战役中，我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡，需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下，如何估测这个距离呢？二、议一议 一位战士想出来这样一个办法：他面向碉堡的方向站好，然后调整帽子，使视线通过帽檐正好落在碉堡的底部.然后，他转过一个角度，保持刚才的姿态，这时视线落在了自己所在岸的某一点上.接着，他用步测的办法量出自己与那个点的距离，这个距离就是他与碉堡间的距离.12ABDC战士的身高AD不变,战士与地面是垂直的(AD⊥BC) 视角∠1=∠2,战士要测的是敌碉堡(B)与我军阵地(D)的距离，BD与DC之间有什么关系，理由是什么？（图1）12ABDC解：在△ADB与△ADC中，有∴△ADB≌△ADC (ASA) .∴DB=DC (全等三角形对应边相等).想一想例1 如图2，A，B两点分别位于一个池塘的两端，小明想用绳子测量A，B间的距离，但绳子不够长，你能帮他想个办法吗？ （图2） 一个叔叔帮小明出了这样一个主意：先在地上取一个可以直接到达A点和B点的点C，连接AC并延长到D，使AC=CD;连接BC并延长到E，使BC=CE,连接DE并测量出它的长度，DE的长度就是A，B间的距离.CDE解：在△CED与△CBA中，
有∴△CED≌△CBA (SAS) .∴DE=AB
(全等三角形对应边相等).CDE∴ △ABC≌△EDC(ASA)
∴AB=ED
解：在△ABC与△EDC中，有(全等三角形对应边相等)
练习： 如图，太阳光线AC与A C 是平行的，同一时刻两根高度相同的木杆在太阳光照射下的影子一样长吗？说说你的理由？＇＇四、小 结（2）运用所学有关知识设计合适可行的方案，并进行说明理由的过程（1）应用三角形全等测量距离(构造全等三角形)五、作业课本P-175 [习题5.11]
知识技能 1 题
数学理解 1 题做一做 有如图的一个零件，它的设计图纸不见了，现在想要知道AB的长度，你有什么办法？DCAB