浙教版九年级科学暑期辅导教案第16讲-简单机械
文档属性
| 名称 | 浙教版九年级科学暑期辅导教案第16讲-简单机械 |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2016-08-19 09:34:56 | ||
图片预览


文档简介
学员班级:
年
级:
课
时
数:3课时学员姓名:
辅导科目:
学科教师:
教学主题
简单机械
授课日期及时段
教学过程
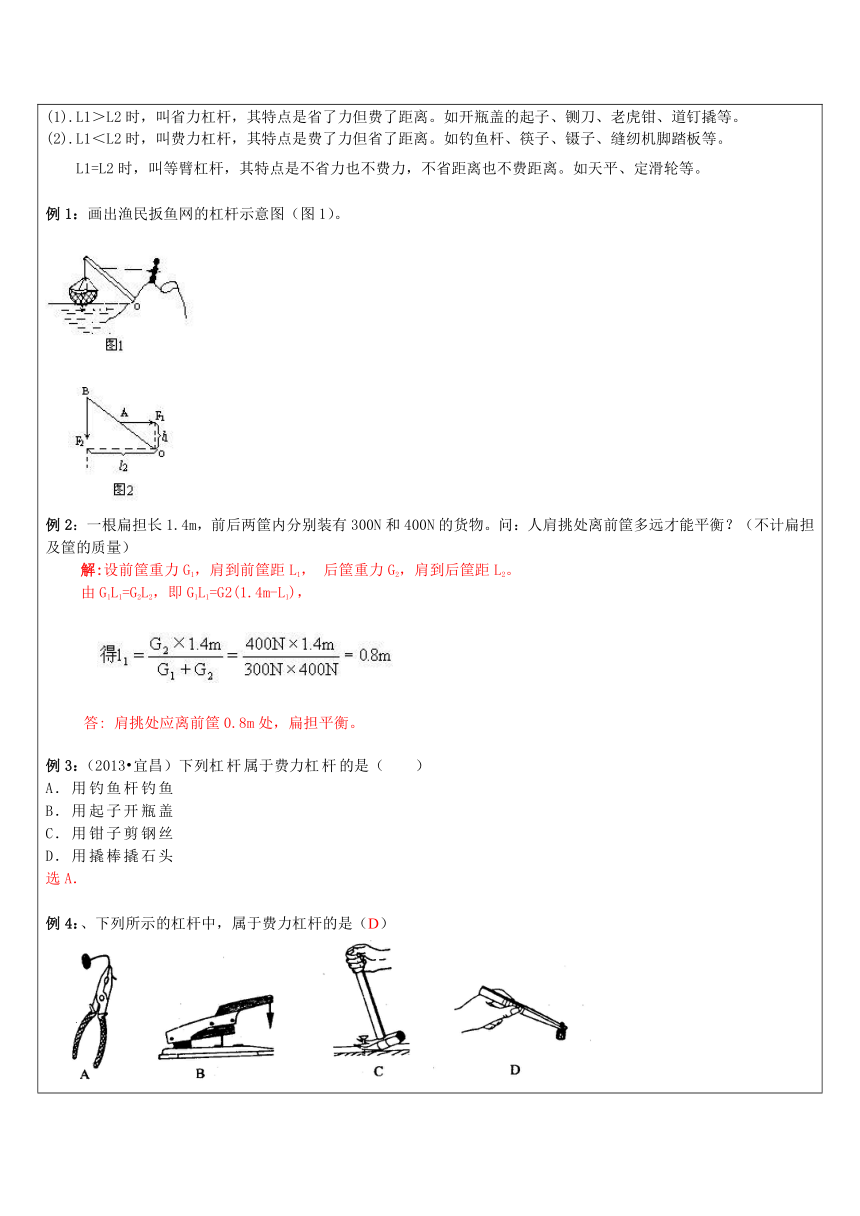
学习杠杆和滑轮相关知识阿基米德说过,给我一个支点,我可以撬起地球,你认为他的说法是否可行 1.杠杆:在力的作用下能绕固定点的硬棒叫做杠杆。2.杠杆的五要素支点:使杠杆绕着转动的固定点。动力:使杠杆转动的力。阻力:阻碍杠杆转动的力动力臂:从支点到动力作用线的垂直距离。阻力臂:从支点到阻力作用线的垂直距离。3.杠杆平衡:指杠杆保持静止状态或匀速转动状态4.研究杠杆的平衡(1).把杠杆的中央支在支架上,调节杠杆两端的螺母,使杠杆在水平位置处于平衡状态(便于直接在杠杆上测出力臂大小)。(2).在杠杆的两端分别挂上不同数量的钩码,在杠杆上左右移动钩码悬挂的位置,直到杠杆再次达到水平位置,处于平衡状态。(3).用直尺量出动力臂L1和阻力臂L2的大小。(4).动力与动力臂的乘积等于阻力与阻力臂的乘积5.杠杆平衡原理:动力×动力臂=阻力×阻力臂,即F1×L1=F2×L2杠杆的分类(1).L1>L2时,叫省力杠杆,其特点是省了力但费了距离。如开瓶盖的起子、铡刀、老虎钳、道钉撬等。(2).L1<L2时,叫费力杠杆,其特点是费了力但省了距离。如钓鱼杆、筷子、镊子、缝纫机脚踏板等。L1=L2时,叫等臂杠杆,其特点是不省力也不费力,不省距离也不费距离。如天平、定滑轮等。例1:画出渔民扳鱼网的杠杆示意图(图1)。 例2:一根扁担长1.4m,前后两筐内分别装有300N和400N的货物。问:人肩挑处离前筐多远才能平衡?(不计扁担及筐的质量)解:设前筐重力G1,肩到前筐距L1,
后筐重力G2,肩到后筐距L2。由G1L1=G2L2,即G1L1=G2(1.4m-L1),
答:
肩挑处应离前筐0.8m处,扁担平衡。例3:(2013 宜昌)下列杠杆属于费力杠杆的是( )A.用钓鱼杆钓鱼B.用起子开瓶盖C.用钳子剪钢丝D.用撬棒撬石头选A.例4:、下列所示的杠杆中,属于费力杠杆的是(D)例5:、下列关于力臂的说法中,正确的是(
B
)A、动力臂是指支点到动力作用点的距离B、阻力臂是指支点到阻力作用线的垂直距离C、动力臂与阻力臂之和等于杠杆长D、当力的作用线通过支点时,力臂最大例6:、下面举出的是几种根据杠杆原理制成的工具:A.钳子;B.铡刀;C.镊子;D.理发剪子;E.剪铁皮剪子;F.天平;G.定滑轮;H.起钉锤;I.指甲刀;J.起子;
K.缝纫机踏板.其中________是省力杠杆,________是费力杠杆,________等臂杠杆.
答案:ABEHIJ;
CDK
;FG
例7:、皮划艇是我国的奥运优势项目之一,比赛中,运动员一手支撑住浆柄的末端(视为支点),另一手用力划桨,此时的船桨是:(
B
)A.等臂杠杆
B.费力杠杆
C.省力杠杆
D.省功杠杆例8:园艺师傅使用如图所示的剪刀修剪树枝时,常把树枝尽量往剪刀轴O靠近,这样做的目的是为了:(
D
)A.增大阻力臂,减小动力移动的距离B.减小动力臂,减小动力移动的距离C.增大动力臂,省力D.减小阻力臂,省力例9:一个杠杆的动力臂与阻力臂之比为4∶1,则该杠杆是________杠杆,动力与阻力之比是________.若此杠杆受到的阻力是60
N,则当动力为________
N时,杠杆处于平衡状态.
答案:省力;1∶4
;15例10:如图所示为小明自制的风力板,口板为迎风板,其迎风面承受风力,b板为压重板,它水平放置,m为压重板上的铁板(a、b板重力不计)。当压重板上铁板重力一定时,风力大到一定程度,风力板就会倾倒,在这过程中,风对迎风板的作用力当作动力,_________当作阻力,压重板上的铁板越重,风力板倾倒时记录的风力越___________.小明通过查阅资料和实验,在压重板上加上重力不同的铁板,制成能测风力1~8级的8个风力板,构成一套风力探测仪。在南风盛行的某地,小明用这套风力探测仪测定当天最强的风力。(1)在开阔地的水平地面放置风力探测仪时,小明应____________________.(2)小明确定当天最强风力的方法是___________________________________答案:(铁板的)重力;大;
(1)将八个风力板的迎风面;
朝南放置;
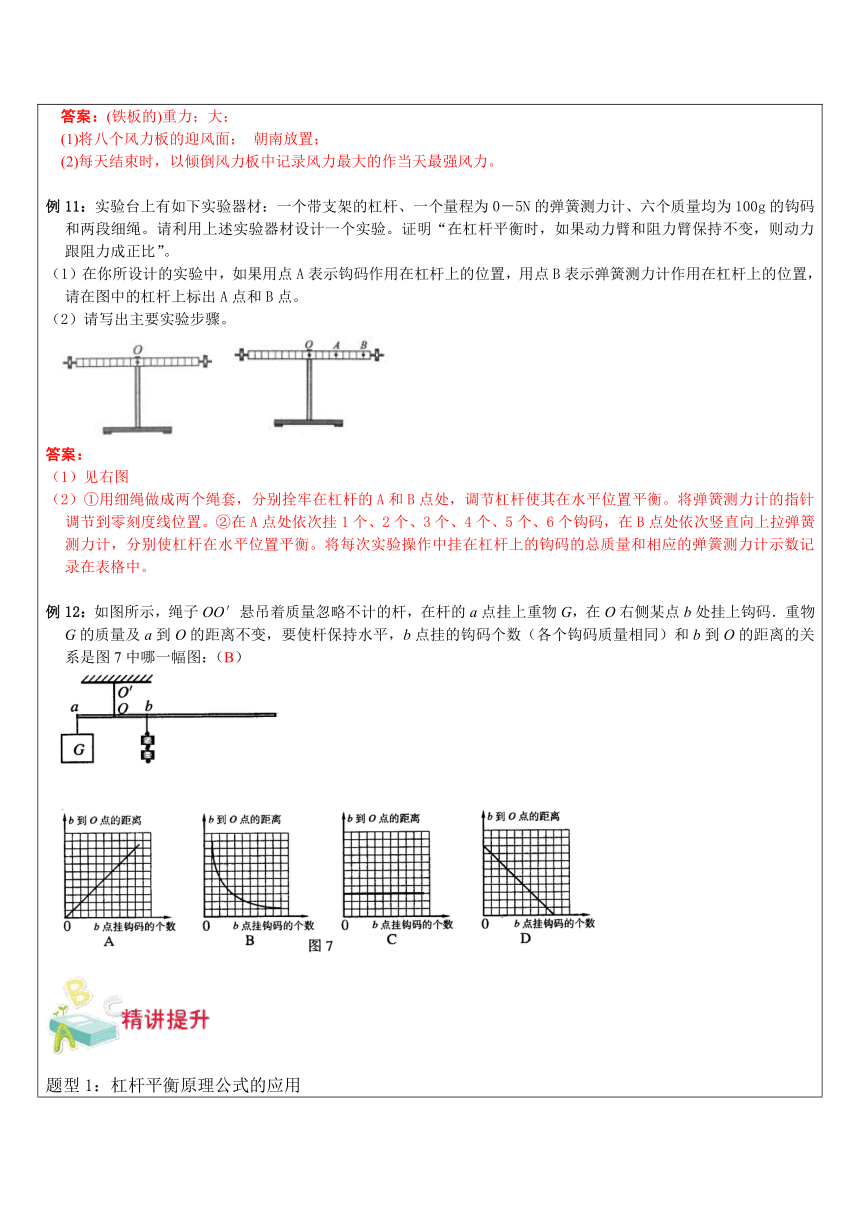
(2)每天结束时,以倾倒风力板中记录风力最大的作当天最强风力。例11:实验台上有如下实验器材:一个带支架的杠杆、一个量程为0-5N的弹簧测力计、六个质量均为100g的钩码和两段细绳。请利用上述实验器材设计一个实验。证明“在杠杆平衡时,如果动力臂和阻力臂保持不变,则动力跟阻力成正比”。(1)在你所设计的实验中,如果用点A表示钩码作用在杠杆上的位置,用点B表示弹簧测力计作用在杠杆上的位置,请在图中的杠杆上标出A点和B点。(2)请写出主要实验步骤。
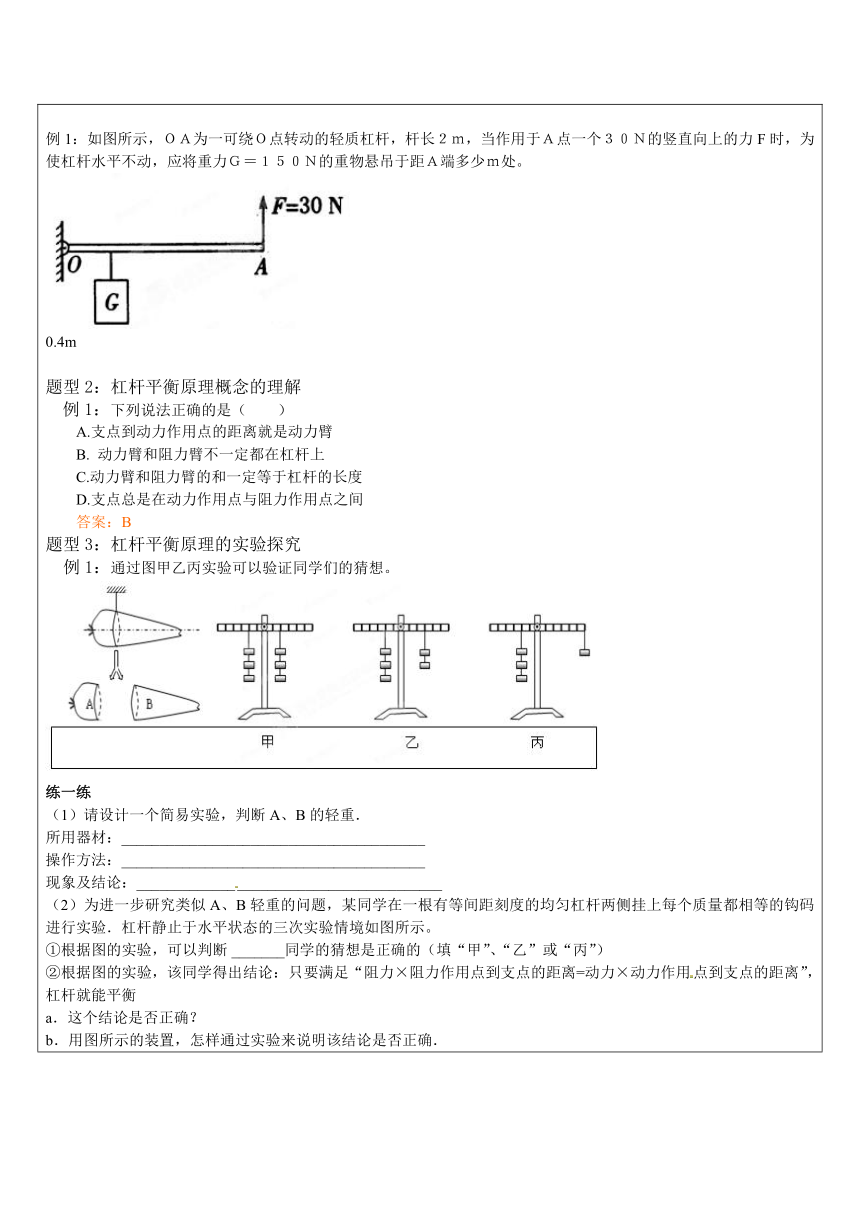
答案:(1)见右图(2)①用细绳做成两个绳套,分别拴牢在杠杆的A和B点处,调节杠杆使其在水平位置平衡。将弹簧测力计的指针调节到零刻度线位置。②在A点处依次挂1个、2个、3个、4个、5个、6个钩码,在B点处依次竖直向上拉弹簧测力计,分别使杠杆在水平位置平衡。将每次实验操作中挂在杠杆上的钩码的总质量和相应的弹簧测力计示数记录在表格中。例12:如图所示,绳子OO′悬吊着质量忽略不计的杆,在杆的a点挂上重物G,在O右侧某点b处挂上钩码.重物G的质量及a到O的距离不变,要使杆保持水平,b点挂的钩码个数(各个钩码质量相同)和b到O的距离的关系是图7中哪一幅图:(B)题型1:杠杆平衡原理公式的应用例1:如图所示,OA为一可绕O点转动的轻质杠杆,杆长2m,当作用于A点一个30N的竖直向上的力F时,为使杠杆水平不动,应将重力G=150N的重物悬吊于距A端多少m处。?0.4m题型2:杠杆平衡原理概念的理解例1:下列说法正确的是(
)A.支点到动力作用点的距离就是动力臂B.
动力臂和阻力臂不一定都在杠杆上C.动力臂和阻力臂的和一定等于杠杆的长度D.支点总是在动力作用点与阻力作用点之间答案:B题型3:杠杆平衡原理的实验探究例1:通过图甲乙丙实验可以验证同学们的猜想。
练一练(1)请设计一个简易实验,判断A、B的轻重.
所用器材:________________________________________
操作方法:________________________________________
现象及结论:________________________________________
(2)为进一步研究类似A、B轻重的问题,某同学在一根有等间距刻度的均匀杠杆两侧挂上每个质量都相等的钩码进行实验.杠杆静止于水平状态的三次实验情境如图所示。①根据图的实验,可以判断 _______同学的猜想是正确的(填“甲”、“乙”或“丙”)
②根据图的实验,该同学得出结论:只要满足“阻力×阻力作用点到支点的距离=动力×动力作用点到支点的距离”,杠杆就能平衡
a.这个结论是否正确?
b.用图所示的装置,怎样通过实验来说明该结论是否正确.
答案:
1:在“探究杠杆的平衡条件”的实验中:(1)所需的实验器材除了两端带有平衡螺母的杠杆、支架、细线、钩码外,还需要_________和__________。(2)张华同学发现杠杆的位置如图所示,则应将平衡螺母向________调节(选填“左”或“右”),使杠杆在_______位置平衡,这样做的目的是
。(3)接下来的实验过程中,张华同学同样使杠杆在
位置平衡,这样做的目的是___________________________________。(4)下列是某同学实验时记录的部分数据,请在空格处填上适当的数据:实验次数动力(N)动力臂(cm)阻力(N)阻力臂(cm)1346218129(5)某同学按照右图进行实验,发现F1·OA和F2·OB并不相等,这是由于___________________________________。答案:(1)弹簧测力计
刻度尺
(2)右
水平
消除杠杆自重对实验的影响
(3)水平
便于测量力臂
(4)2
6
(5)
OA不是F1的力臂2:如图,用测力计将长杆一端A微微抬离地面,测力计示数是F1;同理,用测力计将长杆的另一端B微微抬离地面,测力计示数是F2。则长杆的重力是(测力计保持竖直向上)(
)A.(F1+F2)/2
B.F1+F2
C.F1/F2
D.F1×F2答案:B3
如图(a)所示的杠杆是平衡的,在此杠杆支点两侧的物体下方分别加挂一个和钩码质量一样物体,如图(b)所示,那么,以下说法中正确的是(
)A.杠杆仍然平衡
B.杠杆可能平衡C.杠杆一定不能平衡,杠杆的B端下沉D.杠杆是否平衡与加挂物体的质量多少无关
1.杠杆一条件改变后杠杆将如何转动两边各加一个相等的力2.两边各减一个相等的力3.两边各加一个相等的力臂3.两边各减一个相等的力臂【思考1】如图所示,将体积相同的物体G1、G2分别挂在杠杆的两端,杠杆处于平衡状态。若将两个物体G1、G2同时减小相同的力,则(
)A.杠杆仍能保持平衡
B.杠杆不能平衡,A端下沉C.杠杆不能平衡,B端下沉
D.无法确定杠杆的状态【答案】
C【教学建议】推到这一类题型的结论【思考2】龟兔赛跑结束后,返回途中捡到半个大西瓜(如图),都想独吃,互不相让。争论的结果是:谁的体重大谁吃。可没有弹簧测力计怎么办?这时来了一只老山羊,知道情况后便说“这好办,你们两个各蹲在西瓜的一边,就可以看出哪个重些”。于是兔龟分别蹲到西瓜的一边,结果西瓜还在水平位置平衡如图.老山羊又说:“你们各自向中间移动相等的距离看看”,结果乌龟那边上翘了,兔子很高兴,说:“怎么样,还是我重吧!西瓜归我。”老山羊说:“不对,应该给乌龟。”请你用所学的杠杆知识分析,老山羊的话有道理吗?这个西瓜到底归谁?请用公式推导说出你的理由(西瓜的质量不计)。【答案】证明:设兔子的力臂为L1,重为G1,乌龟的力臂为L2,重为G2
第一次平衡,根据杠杆平衡原理,得G1L1=G2L2
(2分)
当向内移动L后,得
G1(L1-L)>G2(L2-L)
(2分)
即G1L1-G1L
>
G2L2-
G2L
G1L<
G2L
(1分)
得G1<
G2
(1分)
所以老山羊的话有道理
(G直接用m表示扣1分)杠杆中力的方向或杠杆移动后力的大小将如何改变【思考1】在研究杠杆平衡条件的实验中,某同学按图所示的装置来进行操作,他在杠杆的左端悬挂着一个物体,右端用弹簧测力计拉着,使杠杆在水平方向保持平衡,今用手拉着弹簧测力计缓慢地沿图中虚线自位置l移动至位置2,并保持杠杆始终在水平方向平衡,则弹簧测力计的读数
(
)
A.不断增大
B.不断减小
C.先增大后减小
D.先减小后增大【答案】
D【思考2】如图5所示,一根木棒AB在O点被悬挂起来,AO>OC,在A、C两点分别挂有两个和三个相同的钩码,木棒处于水平平衡。如在木棒的A、C两点各增加一个同样的钩码,则木棒(
)
A.绕O点顺时针方向转动B.绕O点逆时针方向转动C.仍保持平衡D.平衡被破坏,转动方向不定【答案】C3.转动时需要的力最小的类型【思考1】如图所示杠杆中,O是支点,在B端挂一个重物,为使杠杆平衡,要在A端加一个力。四个力中数值最小的力是(
)
A.
F1
B.
F2
C.
F3
D.
F4【答案】B【思考2】如图所示,要使杠杆处于平衡状态,在A点分别作用的四个力中,最小的是(
)A.F1
B.F2
C.F3
D.F4
【答案】C概念一、定滑轮:①定义:中间的轴固定不动的滑轮。②实质:定滑轮的实质是:
。③特点:使用定滑轮
。④对理想的定滑轮(不计轮轴间摩擦)F=G;实际生活中,F>G。绳子自由端移动距离SF
(或vF)=
二、动滑轮:①定义:和重物一起移动的滑轮。(可上下移动,也可左右移动)②实质:动滑轮的实质是:
。③特点:使用动滑轮能
。a.理想的动滑轮(不计轴间摩擦和动滑轮重力)则:F=
1
2G
只忽略轮轴间的摩擦则拉力F=
1
2(G物+G动)b.绳子自由端移动距离SF(或vF)=
注意:①可以省一半力,并不是说一定省力一半。a.理想的动滑轮(不计轴间摩擦和动滑轮重力),竖直拉绳最省力且省一半力即F1=
1
2G物;实际生活中,F1>
1
2G物.如图一:理想状态(不计轴间摩擦和动滑轮重力),F2
>F1=
1
2G物;实际生活中,F2
>F1>
1
2G物
。②可以省力,并不是只要用动滑轮就一定省力。如图二:a.理想的动滑轮(不计轴间摩擦和动滑轮重力)则
F=
2G物只忽略轮轴间的摩擦则拉力F=
2G物
+
G动b.绳子自由端移动距离SF(或vF)=
三、滑轮组的特点及其应用①滑轮组的特点:拉动物体时,既能省力又能改变力的方向②滑轮组的计算:使用滑轮组时,滑轮组用几段绳子吊着物体,提起物体所用的力就是动滑轮和重物总重的几分之一,动力作用点移动的距离就等于重物提升高度的几倍③根据一定的要求设计滑轮组绕线的方法:
a.滑轮组的绕线方法与绳子股数的确定滑轮组的绕线方法:常见滑轮组的构成有以下几种情况(如图所示),同一种构成有“定起”和“动起”两种绕线方法(绕线注意:绕线不交叉,不重叠;奇动偶定),要求绕线过程中绳子必须绷紧,具体绕线如图所示:b.绳子股数的确定:一般采用“切割法”定绳子股数,即从定滑轮和动滑轮之间切割(如上图),数出拴在动滑轮框上的绳子和最后从动滑轮引出的拉绳就是承担重物的绳子股数(图中的绳子股数已标出)c.计算:先根据题目中的条件,如绳子能承受的拉力和需要承担的物重计算出需要的绳子段数n(如果计算结果不是整数,一律进上去,例如,计算结果为3.2,则n取4)d.安装:n为偶数时,绳固定端固定在定滑轮上;反之n为奇数时,绳固定端要固定在动滑轮上.具体绕线时,一般先从固定端开始,按顺序由内向外绕,每个滑轮只能绕一次,绳不能相交叉.题型一、作图(用最小的力,应怎么绕线?)例1:
如图所示的甲、乙两个滑轮组,不计滑轮重.要求用最小的力将相同的重物拉起,应选用
滑轮组;请在你选用的滑轮组上画出绳子的绕法;如果物重100N,则用你选用的滑轮组及绕法,最小拉力为
N.[答案]甲;25.[解析]甲、乙两个滑轮组最省力的绕法分别如图甲有4段绳子拉重物,乙有3段绳子拉重物,根据F=G/n
知,甲更省力;则F=G/n
=100N/4
=25N.点评:正确给滑轮组绕绳是本题的基础,在不计绳重和摩擦的情况下,若有n股绳子在拉重物,则F=
G/n,所以n越大越省力,根据图中的滑轮组分别组装省力的情况,再进行比较并计算.例2:
要用最小的力将汽车拉动,试完成绳子的绕法.[解析]将绳子的一端固定在定滑轮的挂钩上,然后将绳子从内向外依次绕过每一只滑轮,共有4段绳子承担总的阻力.如图所示:例3:一个同学站在地面上,要利用如图所示的滑轮组提升重物.已知物重,而绳子最多只能承受的拉力.请你帮他在图中画出符合要求的绳子绕法.[解析]先判断.用“进一法”取.根据“奇拴动,一动配一定,变向加一定”原则,绳子应固定在动滑轮的钩上,由内向外绕.[答案]如图所示题型二、水平类a.
效率为100%
(滑轮组、摩擦力)例1:同一物体沿相同水平地面被匀速移动,如下图所示,拉力分别为F甲、F乙、F丙,不记滑轮与轻绳间的摩擦,比较它们的大小,则(
)
A、F甲<F乙<F丙
B、F甲>F乙>F丙
C、F甲>F乙=F丙
D、F甲=F乙>F丙[答案]B例2:如图所示,重600N的人站在重5400N的船上,通过滑轮把船匀速拉向岸边.人拉绳的力为500N,人和船相对静止.不计绳重和滑轮处摩擦,船受到水的阻力为( )A、500N
B、1000N
C、2500N
D、3000N[答案]
B[解析]因为船做匀速直线运动,所以,船受平衡力的作用,而人和船相对静止,因为F=500N,∴人的磨擦力是500N,方向向右,并且作用在船上,而该滑轮为定滑轮,∴绳子对船的拉力为500N,方向向右,而向右的拉力和船受到水的阻力是一对平衡力,所以,船受到水的阻力f=1000N.故选B.
例3:如图所示,物体A的质量是400g,物体B的体积是10cm3,此时A恰能沿着水平桌面向右做匀速直线运动.若将B始终浸没在水中,并使A沿着水平桌面向左做匀速直线运动时,需要施加0.95N水平向左的拉力.已知动滑轮重为0.3N,不计绳重以及绳和滑轮间的摩擦,则物体B重力为
N.(g取10N/kg)[答案]
0.7[解析]当物体A水平向右匀速运动时,分别对A、B物体受力分析如下图所示:
则根据力的平衡条件可得:f=F1,GB=2F1,f=1/2GB=----------------①
当A向左匀速直线运动时,分别对A、B物体受力分析如下图所示:
∵A物体对水平桌面的压力不变,接触面粗糙程度不变,∴f的大小不变,则根据力的平衡条件可得:F=f+F2,2F2+F浮=GB,
∴F-f=1/2(GB
-
F浮)------------②∵B物体始终浸没在水中,∴V排=V,∴F浮=ρ水gV------------③
由①②③式可得:GB=0.7N;
b.效率为100%
(滑轮组、摩擦力、功)例3:如图所示,置于水平桌面上的物体A重490N,物体B重294N,物体B在匀速下降了40cm的过程中,拉动物体A在水平桌面上匀速移动了一段距离;若用一水平向左的力F拉动物体A,使物体A在5s内匀速移动0.5m(不计动滑轮、绳重以及滑轮轮轴间摩擦),则下列说法正确的是
(
)A、拉力F为294N,拉力F的功率为29.4W
B、拉力F为147N,拉力F的功率为14.7W
C、物体A与桌面的滑动摩擦力为294N
D、绳子拉力对物体B所做的功为73.5J[答案]AD[解析]当A向右做匀速直线运动,水平方向上受到水平向右的拉力和向左的摩擦力,f=1
2
GB=1
2
×294N=147N;当A向左做匀速直线运动,水平方向上受到水平向左的拉力、向右的摩擦力、B对A的拉力;滑动摩擦力的大小跟压力大小和接触面的粗糙程度有关,压力不变,接触面的粗糙程度不变,摩擦力不变,所以向右的摩擦力为:f=147N.故C错误;A向左做匀速直线运动,受到平衡力的作用,A受到的水平向左的拉力为:F=f+GB
2
=147N+147N=294N;A的移动速度V=S
t
=0.5m
5s
=0.1m/s;拉力F的功率为P=FV=294N×0.1m/s=29.4W;故A正确;B错误;绳子拉力对物体B所做的功为W=GB
2
S=294N
2
×0.5m=73.5J,故D正确.故选AD.例4:如图所示,物体A的质量m
=12kg,在拉力F的作用下,物体A以0.1m/s的速度在水平面上做匀速直线运动,弹簧测力计的示数为12N,忽略滑轮与绳子的摩擦力以及滑轮、弹簧测力计和绳子所受的重力,并且绳子足够长。求:(1)物体A与水平面间摩擦力f的大小;(2)拉力F的大小;(3)物体A运动10s
的过程中,拉力F所做的功。(提示:拉力做功W2=Fs
,W2=W1,克服摩擦力做功W1=f
h)[答案]
(1)因做匀速直线运动,则:f=F示=12N(2)如图所示,作用在动滑轮轴上的拉力:F=2f=2×12N=24N(3)W=FS=24N×0.1m/s×10s×1/2=12J
[解析](1)因为物体A做匀速直线运动,所以物体受到绳子的拉力大小等于其所受摩擦力大小,而绳子拉力的大小由弹簧秤测出,所以f=12N
(2)由动滑轮的作用可知F=2f=2×12N=24N
(3)运动10秒钟,物体A通过的距离
S=v
t=0.1m/s×10s=1m
拉力F通过的距离S'=S/2=1m/2=0.5m
拉力F所做的功:W=
F
S'=24N×0.5m=12Jc.效率不为100%
(滑轮组、摩擦力、效率)例5:如右图所示,物体在水平面上做匀速直线运动,拉力F=60
N,该装置的机械效率为0.7,则物体受的摩擦力大小是(
)A、60
N
B、126
N
C、180
N
D、257.1
N[答案]B[解析]η=fh
FS
=fh
F×3h
=f
3F
;∴f=3Fη=3×60×70%N=126N.故选B.d.效率不为100%
(滑轮组、压强、机械效率)例5:用如图所示的滑轮组去拉物体A,已知A物质的密度是2
×103kg/m3,底面积是0.3m3,重力为600N。物体A在F=100N的拉力作用下,沿水平方向匀速前进了2m。(g取10N/kg)求:(1)物体A对水平地面的压强是多少
(2)物体A的体积是多大 (3)若该装置的机械效率为80%,物体A在水平方向上受到的阻力是多少?[答案](1)物体A对水平地面的压强是2×103.(2)
物体A的体积是0.03m3.(3)
物体A在水平方向上受到的阻力是160N.[解析](1)∵物体A在水平地面上作匀速直线运动,
∴F=G=600N,∴P=
F
/S=
600N/0.3m2=2×103Pa.(2)物A的质量m=
G/g
=
600N/10N/Kg=60Kg,物A的体积V=
m/ρ
=
60Kg
/2×103Kg/m3=0.03m3(3)拉力F所做的功W总=FS=100N×2×2m=400J,克服阻力所做的功W有=W总η=400J×80%=320J,物A所受阻力f=
W有/h=320J/2m=160N.题型三、竖直类a.
效率为100%(不计机械自重和摩擦)例1:如下图所示,用四个滑轮组分别匀速提升重力相同的物体,若不计滑轮重、绳重及摩擦,其中用力最小的是(
)
A.F1
B.F2
C.F3
D.F4
[答案]B例2:由两个动滑轮和两个定滑轮组成的滑轮组,站在地面的人用力向下拉绳,提起重为1000N的物体.问:(1)若不计摩擦和滑轮的重,所用拉力F是多大 (2)若实际所用拉力F为300N,则动滑轮总重是多少 (3)物体升高0.1m时,绳子的自由端所移动的距离是多少 [答案]
(1)250N;(2)200N;(3)0.4m[解析](1)因不计摩擦和滑轮的重量,所以拉力F=G/n=1000N/4=250N;(2)若实际所用拉力F为300N,则动滑轮总重G′=300×4N-1000N=200N;(3)物体升高0.1m时,绳子的自由端所移动的距离s=nh=4×0.1m=0.4m;
例3:如图所示,吊篮的重力为400N,动滑轮的重力为50N,定滑轮重力为40N,人的重力为600N,人在吊篮里拉着绳子不动时需用力(
)A.218N
B.220N
C.210N
D.236N[答案]C[解析]设人对绳的拉力F,将人、吊篮和动滑轮视为一个整体,此时整体处于静止状态,整体重力由5段绳子承担,所以有5F=.所以b.效率不为100%
(滑轮组、机械效率)例4:
用一个动滑轮、一个定滑轮组成的滑轮组来匀速提升重物G,如图所示,已知物重G=600N,拉力F=250N,求10秒内将重物升高0.5m的过程中,所做的有用功,额外功,及拉力的功率为多大?若所提升重物重力为750N,拉力为多大?(不计绳重和摩擦力).[答案]
所做的有用功为300J,额外功为75J,拉力的功率为37.5W,若所提升重物重力为750N,拉力为300N.[解析](1)由图可知,n=3,绳子自由端移动的距离s=nh=3×0.5m=1.5m,有用功W有=Gh=600N×0.5m=300J,总功W总=Fs=250N×1.5m=375J,额外功W额=W总-W有=375J-300J=75J;P总=W总
t
=375J
10s
=37.5W;(2)∵F=1
n
(G+G动),∴G动=3F-G=3×250N-600N=150N,∴所提升重物重力为750N,拉力F′=1
3
(G′+G动)=1
3
×(750N+150N)=300N.例5:建筑工人用如图所示的装置把重400N的物体匀速提升3m.所用的手拉力为300N.则该工人所做的有用功为
J,总功为
J,该滑轮组的机械效率是
(保留三位有效数字).若用该装置提升500N的重物,此时滑轮组的机械教率将
(填“变大”、“变小”或“不变”)[答案]
1200,1800,66.7%,变大[解析]由图知,有2段绳子承担物重,若重物提升h=3m,绳子末端移动距离s=2h=2×3m=6m.拉力做的有用功:W有用=Gh=400N×3m=1200J;拉力做的总功:W总=Fs=300N×6m=1800J.该机械的效率:η=W有用
W总
=1200J
1800J
≈66.7%.当提升重物的重力增加,做的有用功就变大,而额外功几乎不变,故机械效率变大.c.
效率不为100%
(滑轮组、功率、机械效率)例6:在小型建筑工地,常用简易的起重设备竖直吊运建筑材料,其工作原理相当于如图所示的滑轮组。某次将总重G为4000
N的砖块匀速吊运到高为10
m的楼上,用时40
s,卷扬机提供的拉力F为2500
N。求在此过程中:(1)有用功;(2)拉力F的功和功率;(3)滑轮组的机械效率。[答案]
(1
)4
×104J;(2
)5
×104J,1.25×103w;(3)80%[解析](1
)W有=Gh=4000N×10m=4
×104J
(2
)W总=Fs=F
×2h=2500N×2×10m=5
×104J,P=W/S=FV=5
×104J/40s=1.25×103w.(3)η=
W有/
W总=80%。d.效率不为100%
(滑轮组、浮力、机械效率)例7:如图所示,重物A是体积为10dm3,密度为7.9
×103
kg/m3的实心金属块,将它完全浸没在水中,始终未提出水面。若不计摩擦和动滑轮重,要保持平衡,求:(1)作用于绳端的拉力F是多少?(2)若缓慢将重物A提升2m,拉力做的功是多少?(3)若实际所用拉力为400N,此时该滑轮的效率是多少?(g=10N/kg)[答案]
172.5N;1380J;43.1%[解析](1)物体A的体积为V=10dm3=0.01m3,则完全浸没在水中时,V排=V=0.01m3,金属块受到的浮力:F浮=ρ水gV排=ρ水gV=1×103kg/m3×10N/kg×0.01m3=100N;金属块的重力:G=mg=ρVg=7.9×103kg/m3×0.01m3×10N/kg=790N,∵由图可知,动滑轮是由4股绳子承担,在不计摩擦和动滑轮重的条件下,∴作用于绳端的拉力:F=1/4(G-F浮)=1/4(790N-100N)=172.5N.(2)若缓慢将重物A提升2m,因为n=4,所以s=nh=4×2m=8m,拉力做的功:W=Fs=172.5N×8m=1380J.(3)若实际所用拉力为400N,则总功为:W总=Fs=400N×8m=3200J;使用滑轮组所做的有用功:W有用=(G-F浮)h=(790N-100N)×2m=1380J,此时该滑轮的效率此时该滑轮的效率:η=W有用
W总
×100%=1380J
/3200J
×100%≈43.1%.1.有用功:为达到目的必须做的功;额外功:为了达到目的并非需要又不得不做的功;总功:有用功和额外功的总和。
机械效率的计算:对于滑轮组而言的公式运用(不可直接用):;对于水平方向上的滑轮组及滑轮组与浮力组合、与斜面组合时,可牢记针对滑轮组的机械效率,力均是作用在滑轮组上的,进行受力分析找力并求该力所作的功,分清有用功和总功,运用基本公式求机械效率。
3.提高机械效率的方法:由公式可知,当有用功一定时,额外功越小,机械效率越高,因此设法减小额外功可以提高机械效率。如减轻动滑轮本身的重量,加润滑油可以减小摩擦等;当额外功一定时,有用功越大,机械效率越高,因此增大有用功可以提高机械效率,如增加物重可以提高机械效率。机械效率具有“可变性”。由可知,如果该机械的额外功(W额外)一定,有用功()越大,机械效率越大。因此,增加物重能增大机械效率。由上面的公式还可以知道:当有用功一定时,额外功越小,则机械功率越大。因此设法减小额外功可以提高机械功率。如减轻机械本身的重量,加润滑油以减少摩擦,都可以不同程度地减少额外功,提高机械效率。
4.与斜面效率有关的公式:
;;;根据,可知,利用这个式子可求物体与斜面间的摩擦力。斜面机械效率与斜面的坡度有关,坡度越大,物体与斜面间压力越小,滑动摩擦力越小,提升相同高度,物体走过的路程越短,因此克服摩擦做的额外功越小,机械效率越大。5.杠杆机械效率:6.组合机械的机械效率:1、机械效率的认识和比较1.甲吊车比乙吊车的机械效率高,当它们分别把相同质量的物体匀速提升相同高度时,则( ) A.甲吊车的电动机做的有用功较多 B.乙吊车的电动机做的额外功较多 C.甲吊车的电动机做的总功较多 D.甲、乙两吊车的电动机做的总功相同解答:A、分析知甲乙吊车做的有用功相同.此选项错误,不符合题意;B、两辆吊车做的有用功相同,乙吊车做的额外功较多,所以乙的效率较低.此选项正确,符合题意;C、已知甲吊车的机械效率高,有用功相同,如果甲吊车的总功较多就与效率高矛盾.此选项错误,不符合题意;D、两吊车做的有用功相同,如果总功也相同,则机械效率相同.此选项错误,不符合题意.故选B.2.下列关于机械效率的说法正确的是( ) A.机械效率不可能达到100% B.随着科学技术的发展,机械效率可能会大于100% C.滑轮组的机械效率一定大于动滑轮的机械效率 D.杠杆的机械效率一定大于动滑轮的机械效率解答:AB、科技无论怎么发展,机械元件之间摩擦都不能消除,机械效率不可能达到100%,更不会大于100%.所以选项A正确,选项B错误.CD、滑轮组的机械效率、动滑轮的机械效率、杠杆的机械效率高低,跟机械的重、提起物体的重、摩擦、绳重等有关,在这些不能确定的情况下不能确定哪种机械的机械效率的更大一些.选项CD都错误.故选A.3.如图所示,小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,用甲滑轮所做的总功为W1,机械效率为η1;用乙滑轮所做的总功为W2,机械效率为η2.若不计绳重与摩擦,则( ) A.W1=W2,η1=η2B.W1=W2,η1<η2C.W1<W2,η1>η2D.W1>W2,η1<η2解答:因为小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,所以两种情况的有用功相同;当有用功一定时,利用机械时做的额外功越少,则总功越少,机械效率越高.又因乙滑轮是动滑轮,所以利用乙滑轮做的额外功多,则总功越多,机械效率越低.即W1<W2,η1>η2,所以C选项正确.故选C.4.在不计摩擦和绳子质量的情况下,分别使用定滑轮、动滑轮、滑轮组(两个定滑轮和两个动滑轮)匀速提升同一物体到同一高度处,其机械效率分别为η定、η动、η组,则下列选项正确的是( ) A.η组<η动<η定B.η定<η动<η组C.η动<η定<η组D.η定<η组<η动解答:∵匀速提升同一物体到同一高度处,∴三种情况下做的有用功相同,大小都为W有用;∵不计绳子质量和摩擦,∴使用滑轮做的额外功:W额=G轮h,又∵使用定滑轮、动滑轮、滑轮组的动滑轮的个数为0、1、2,∴使用定滑轮、动滑轮、滑轮组做的额外功:W额1<W额2<W额3,∵W总=W有用+W额,∴三种情况下做的总功:W定<W动<W组,∵η=,∴使用定滑轮、动滑轮、滑轮组的机械效率:η定>η动>η组.故选A.滑轮组的机械效率1.如图所示,不计摩擦,把重G=16N的物体匀速提起所用的拉力F=10N,则关于该动滑轮的说法中错误的是( ) A.动滑轮重4N B.使该用动滑轮要费距离 C.该动滑轮的机械效率为80% D.提升物体的速度越快,机械效率越高解答:A、根据F=(G物+G动)得G动=2F﹣G物=2×10N﹣16N=4N,所以A正确.B、动滑轮可以省一半的力,但费距离.所以B正确.C、η=×100%=×100%=×100%=80%,所以C正确.D、提升物体的速度快,则做功快,功率大,但效率不变.所以D错误.故选D.2.如图所示,小丽用滑轮组匀速提升一个重为600N的物体,物体上升的速度为0.1m/s,人拉绳的力F为250N,不计绳重和摩擦,下列说法不正确的是( ) A.人拉绳做功的功率为75WB.滑轮组的机械效率为80% C.绳子自由端移动的速度为0.3
m/sD.动滑轮重为100N解答:∵物体上升的速度v=0.1m/s,n=3∴v′=3v=3×0.1m/s=0.3m/s;故C正确;人拉绳做功的功率P===Fv′=250N×0.3m/s=75W,故A正确;滑轮组的机械效率:η=====80%;故B正确;∵F=(G物+G轮)即250N=(600N+G轮)G轮=150N,故D错误.故选D.3.如图所示,利用轻质滑轮组匀速拉动水平地面上重为300N的物体,拉力F的大小为30N.若物体和地面之间的摩擦力大小为45N,则A处的拉力大小和滑轮组的机械效率分别为( ) A.45N、50%B.45N、75%C.60N、50%D.60N、75%解答:①物体在水平地面上做匀速运动,则此时A处绳子的拉力与物体与地面之间的摩擦力是一对平衡力,∵物体和地面之间摩擦力为f=45N,∴A处的拉力大小为FA=f=45N.②从图可知,由2段绳子与动滑轮相连,则S=2s物,∵F=30N,f=45N,∴滑轮组的机械效率为:η======75%.故选B.4.小明用如图所示滑轮组将一个放在水平地面上的物体匀速拉动,物体移动了3m,物体重为2000N,与地面的接触面积为0.5m2,运动过程中物体受到的摩擦力为450N,绳子自由端受到的拉力F
为200N,求:(1)物体对地面的压强;(2)拉力F做的功;(3)该装置的机械效率.解答:(1)物体对地面的压力:F=G=2000N,物体对地面的压强:p===4000Pa;(2)由图可知:n=3,绳子自由端移动的距离:s=ns′=3×3m=9m,拉力F做的功:WF=F拉s=200N×9m=1800J;(3)该装置的机械效率:η=×100%=×100%=×100%=×100%=×100%=75%.答:(1)物体对地面的压强为4000Pa;(2)拉力F做的功为1800J;(3)该装置的机械效率为75%.5.中华神州打捞公司用如图所示的滑轮组,打捞沉在长江三峡江底一个方形物体.物体上表面距离水面50米,重力为2400N,体积为0.2m3.打捞时匀速提升该物体.(g=10N/kg
ρ水=1.0×103kg/m3)
求:①物体沉在江底时,上表面受到的水的压强;②物体在露出水面之前受到水的浮力;③物体在露出水面之前,人的水平拉力F【设物体在露出水面之前此装置的机械效率为80%】解答:(1)物体上表面受到的压强为P=ρgh=1.0×103kg/m3×10N/kg×50m=5×105Pa;(2)物体露出水面前受到的浮力为F浮=ρ液gV排=1.0×103kg/m3×10N/kg×0.2m3=2000N;(3)物体出水前,滑轮组对物体的拉力为F′=G﹣F浮=2400N﹣2000N=400N作用在绳子末端的拉力为F===250N.答:(1)物体上表面受到的压强为5×105Pa;(2)物体露出水面前受到的浮力为2000N;(3)物体出水前,作用在绳子末端的拉力为250N.斜面的机械效率1.如图甲所示,王大叔正吃力地把一重物送往高台,放学回家的小鹏看见后急忙前去帮忙.他找来一块木板,搭成图乙所示的斜面,结果非常轻松地把重物推到了高台上.关于这两种方法,下列说法中正确的是( ) A.王大叔克服重力做功较多B.两人做同样多的有用功 C.小鹏做功的功率要大些D.甲、乙两种情况下的机械效率一样解答:A、B、这两种方法,都把重物推到了高台上,两人做同样多的有用功,克服重力做功相同.选项A错误、选项B正确;C、功率等于功与时间是比值,由于题中没有给出时间,不能确定哪个做功的功率大.此选项错误;D、由于乙中情况需要克服摩擦做功,所以乙种情况下的机械效率小.此选项错误.故选B.2.如图,某同学用F=300N的力将重为400N的物体从斜面底端匀速拉到顶端,斜面的高为3m,底边为4m,斜面的机械效率( ) A.93.75%B.80%C.56.25%D.45%解答:有用功:W有用=Gh=400N×3m=1200J,斜面高3m,斜面底边是4m,所以斜面长度为:s==5m,总功:W总=Fs=300N×5m=1500J,机械效率:η===80%.故选B.3.如图所示,斜面长为3m,高为lm,工人用400N沿斜面方向的力将重为840N的箱子推到车上.在这过程中( ) A.有用功是400J,总功是840JB.有用功是840J,额外功是400J C.总功是12O0J,机械效率是7O%D.有用功是400J,机械效率是7O%解答:对木箱做的有用功:W有=Gh=840N×1m=840J,利用斜面做的总功:W总=Fs=400N×3m=1200J;额外功W额=W总﹣W有用=1200J﹣840J=360J,斜面效率:η==×100%=70%.故选C.4.一个重为G的物体沿如图所示的左右两个斜面,被推上同一个平台,左斜面长为L1,是右斜面长L2的1/2,且沿两个斜面推动物体时所受摩擦力一样大,那么两个斜面相比( ) A.用左斜面省力少,机械效率比右高 B.用右斜面省力多,机械效率比左高 C.两个斜面做的有用功一样,效率也一样 D.条件不足,无法判断解答:∵左斜面倾斜角度大于右斜面,∴用右斜面更省力;由题知,沿两个斜面推动物体时所受摩擦力一样大,f1=f2,L1<L2,∵W额=fL,∴利用两个斜面做额外功:W额1<W额2,∵W有用=Gh,G、h相同,∴利用两个斜面做的有用功:W有用1=W有用2,∵W总=W有用+W额,∴利用两个斜面做的总功:W总1<W总2,∵η=,∴利用两个斜面的效率η1>η2.由上述分析可知,用左斜面省力少,机械效率比右高.故选A.5.如图所示,斜面长6m,高3m,用沿斜面向上、大小为100N的拉力F使物体在5s内沿斜面移动了2m,下列说法正确的是( ) A.滑轮组的机械效率是40%B.物体重300N C.拉力F做的功是600JD.拉力F的功率是40W解答:因条件不足,无法计算物体重和机械效率,故A、B错.拉力F移动的距离:s=3s′=3×2m=6m;拉力F所做的总功:W总=Fs=100N×6m=600J,故C正确;拉力F做功的功率:P===120W,故D错;故选C.思考:若物体的重力为300N,整个装置的机械效率为多少?物体所受摩擦力为多大?滑轮组机械效率能求出吗?杠杆的机械效率1.小明在探究利用杠杆做功的实践活动中,所用的杠杆是一根质量均匀、重为5N的硬棒,他将棒的一端固定,把重为15N的物体挂在棒的中点,然后用手缓慢竖直向上提起棒的另一端,如图所示,若把物体提升了10cm,则小明作用在杠杆上的拉力是
N,此过程中杠杆的机械效率是
.解答:15N的物体和5N杠杆的重作用在杠杆中点上,动力竖直作用在杠杆的末端,动力臂是阻力臂的2倍,所以动力是阻力的二分之一,所以F=(G+G杆)=(15N+5N)=10N.使用任何机械都不省功,动力是阻力的二分之一,动力移动的距离是阻力移动距离的2倍,有用功:W有=Gh=15N×h,总功:W总=Fs=10N×2h,机械效率:η===75%.故答案为:10;75%.2.如图所示,用竖直向上的力匀速拉动较长的杠杆,使重为18N的物体缓慢升高0.1m,拉力大小F=8N,拉力移动的距离为0.25m.拉力所做的功为
J,有用功为
J,杠杆的机械效率为
%.解答:有用功为W有=Gh=18N×0.1m=1.8J;拉力所做的功为W总=Fs=8N×0.25m=2J,杠杆的机械效率为η=×100%=×100%=90%.故答案为:2;1.8;90.机械效率相关实验1.小红在探究“影响滑轮组机械效率高低的因素”时,提出下列假设:(1)机械效率可能跟动滑轮有关(2)机械效率可能跟被拉物体上升的高度有关(3)机械效率可能跟被拉物体重有关(4)机械效率可能跟承受绳子的段数有关然后小婷设计了如图所示的2组实验进行对比,来验证小红提出的假设,则该实验验证的假设是( ) A.(1)B.(2)C.(3)D.(4)解答:猜想滑轮组机械效率可能跟动滑轮、物体上升的高度、物体重力、绳子的段数有关,探究滑轮组机械效率跟其中一个因素的关系时,控制其它因素不变.如图,动滑轮、物体上升的高度、物体重力可以相同,绳子的段数不同,所以如图探究滑轮组机械效率跟承受绳子的段数的关系.故选D.2.在“测定动滑轮机械效率”的实验中,小明用如图所示的动滑轮提升钩码,改变钩码的数量,正确操作,实验数据如下:实验序号钩码重钩码上升的高度h/cm拉力F/N绳端移动的距离s/cm①1.020.000.740.00②2.020.001.240.00③3.020.001.740.00(1)实验时,用手
拉动弹簧测力计,使持在动滑轮下的钩码缓缓上升.(2)第①次实验时测得动滑轮的机械效率为
.(3)第③次实验时,钩码上升的速度为0.05m/s,则拉力的功率为
W.(4)由表中实验数据分析可知,同一动滑轮,所提升物重增大,机械效率将
(选填“增大”、“减小”或“不变”).解答:(1)在实验时,应用手匀速拉动弹簧测力计,使挂在动滑轮下的钩码缓缓上升.(2)η1=×100=×100%≈71.4%(3)由第三次数据知,s=2h,所以绳子移动速度为物体上升速度的2倍.P总===Fv=1.7N×0.05m/s×2=0.17W(4)根据表格中数据,②的效率η2=×100%=×100%≈83.3%η3=×100%=×100%≈88.2%根据三次的机械效率及物重的变化可得同一动滑轮,所提升物重增大,机械效率将增大.故答案为:(1)匀速;(2)71.4%;(3)0.17;(4)增大.3.斜面是一种简单机械,生活中人们常常利用它来省力.小明想搽究“斜面的机械效率与斜面的倾斜程度的关系”.于是他找来木块A、长木扳B、三个高度不同的长方体C和一把弹簧测力计进行实验,实验装置如图所示.(1)除上述器材外,小明要完成实验还需要的一种器
材是
;(2)在实验过程中,应沿斜面向上拉动术块,使木块做
运动;(3)实验记录数据如下表,则第3次实验时斜面的机械效率为
;(4)分析比较下表中的实验数据,可得到的结论是:斜面越陡
.实验次数斜面倾斜程度木块重G/N斜面高度h/m沿斜面的拉力F/N木块沿斜面移动的距离S/m斜面的机械效率1较缓50.23.30.560.6%2较陡50.253.80.565.8%3最陡50.34.20.5解答:(1)要测量斜面的高度和木块沿斜面移动的距离就要使用长度的测量工具﹣﹣﹣刻度尺;(2)为了保证弹簧测力计的示数稳定,就要让木块做匀速直线运动;(3)第三次实验时,斜面的机械效率η==≈71.4%;(4)由图中数据可知:斜面的倾斜程度越大,斜面的机械效率越高.故答案为:(1)刻度尺;(2)匀速直线;(3)71.4%;(4)斜面的机械效率越高.4.用如图所示的实验装置测量杠杆的机械效率.实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升.(1)实验中,将杠杆拉至图中虚线位置,读出测力计的示数F为
N,钩码总重量G为1.0N,钩码上升高度h为0.1m,测力计移动距离s为0.3m,则杠杆的机械效率为
%.(2)为了进一步研究杠杆的机械效率与哪些因素有关,一位同学用该实验装置,先后将钩码挂在A、B两点,测量并计算得到下表所示的两组数据:次数钩码悬挂点钩码总重G/N钩码移动距离h/m拉力F/N测力计移动距离s/m机械效率η/%1A点1.50.100.70.3071.42B点2.00.151.20.3083.3根据表中数据,能否得出“杠杆的机械效率与所挂钩码的重有关,钩码越重其效率越高”的结论?答:
;请简要说明理由(写出一条即可):
.解答:(1)由图可知,弹簧测力计的分度值是0.1N,所以它的示数是0.5N;在实验过程中,有用功是:W有用=Gh=1.0N×0.1m=0.1J,总功是:W总=Fs=0.5N×0.3m=0.15J,所以杠杆的机械效率是:η=×100%=×100%=66.7%.(2)分析机械效率的影响因素应采取控制变量法,研究提起的物重和机械效率的关系时,应保持钩码所挂位置不变,而实验中,两次钩码悬挂的位置是不同的;同时,还应进行多次实验,分析多组数据,才能得出有说服力的正确结论,只凭一次实验数据做出结论是不科学的.故答案为:(1)0.5;
66.7;(2)不能.两次实验时,钩码没有挂在同一位置,同时改变两组条件,数据不宜直接比较(或仅根据一次对比实验所得结论是不可靠的).(此环节设计时间在10分钟内)(以学生自我总结为主,TR根据教案中的总结进行引导为辅,为本次课做一个总结回顾;总结方式可以多种多样,如画思维导图、默想回忆、抢答形式等。教案中给到重难点/易错点等的总结条目。)1.
2.3.1.
包含预习下次课内容和复习本次课内容两部分;
2.
建议作业量不宜过多,最好控制在学生30分钟内能够完成;3.
每节课前教师对作业进行批改与讲解;本次课复习1.如图所示,轻质木杆AB可以绕O点转动,OA的长度是OB的三倍,A端细线下所挂280N的重物静止在水平地面上,在B点用600N的动力竖直向下拉动,木杆静止不动,则重物对水平地面的压力为
N,此木杆为
(填“省力”
“费力”或“等臂”)杠杆。答案:80;费力2.
如图所示,—根铁棒在水平拉力F的作用下,以O点为转轴,由竖直位置逆时针匀速转向水平位置的过程中,动力F与动力臂L的大小变化是A.F增大,L增大
B.F减小,L减小
C.F增大,L减小
D.F减小,L增大答案:C3.(2011年中考·浙江义乌卷)如图所示,一块厚度、密度均匀的长方形水泥板放在水平地面上,用一竖直向上的力,欲使其一端抬离地面,则(
)A.F甲>F乙,因为甲方法的动力臂长
B.F甲F乙,因为乙方法时阻力臂短
D.F甲=F乙,因为动力臂都是阻力臂的2倍答案:D
4.如图所示,长度为2L的轻质细杆可在竖直面内绕竖直墙壁上的固定转轴O无摩擦地转动.AB为一段长度为1.5L的不可伸长的轻绳,绳AB能承受的最大拉力为F,现将绳的两端AB分别与墙壁及杆相连,使杆始终保持水平.则杆的末端C处可悬挂重物的最大重力为
.答案:3F/85.如图所示,轻质杠杆OA中点悬挂重为60N的物体,在A端施加一竖直向上的力F,杠杆在水平位置平衡,则力F的大小是_______________,保持F的方向不变,将杠杆从A位置匀速提升到B位置的过程中,力F将_____________(选填“变大”、“变小”或“不变”)。答案:30N;不变6.如图甲所示,小明在探究“杠杆的平衡条件”实验中所用的实验器材有:杠杆、支架、弹簧测力计、刻度尺、细线和质量相同的钩码若干个。(1)实验前,将杠杆中点置于支架上,当杠杆静止时,发现杠杆右端下沉。此时,应把杠杆两端的平衡螺母向 (选填“左”或“右”)调节,使杠杆在不挂钩码时,保持
并静止,达到平衡状态。这样做的好处是:便于在杠杆上直接测量
。(2)杠杆调节平衡后,小明在杠杆上A点处挂4个钩码,在B点处挂6个钩码杠杆恰好在原位置平衡。于是小明便得出了杠杆的平衡条件为: 。他这样得出的结论是否合理? ;为什么? 。(3)实验结束后,小明提出了新的探究问题:“若支点不在杠杆的中点时,杠杆的平衡条件是否仍然成立?”于是小组同学利用如图乙所示装置进行探究,发现在杠杆左端的不同位置,用弹簧测力计竖直向上拉使杠杆处于平衡状态时,测出的拉力大小都与杠杆平衡条件不相符。其原因是:
。答案:(1)左;水平;力臂
(2)F1
l1=
F2
l2;不合理;结论具有偶然性(结论没有普遍性)(3)杠杆自重的影响。7.如图所示,重500N的人站在重2500N的船上,用滑轮组把船匀速拉向岸边,人和船相对静止..不计绳重和滑轮轴摩擦,人拉绳的力为300N,求船受到水的阻力为(
)A、900N
B、450N
C、1100N
D、2700N8、如图中的水平桌面足够长,不计托盘质量和滑轮与绳的摩擦.物体A重10N,当物体B重为2N时,物体A保持静止,这时A物体受到的摩擦力为
N;当物体B重为3N时,物体A向右做匀速直线运动,运动一段时间托盘着地,此后物体继续运动一段时间,此时物体A受到的摩擦力是
N.方向是
.[答案]
2;3;水平向左.
9、如图所示,船和人总重1500N,船上的人用力F=30N的拉力拉绳,船作匀速直线运动,则船受到水的阻力为( )
A.30NB.60NC.90ND.500N[答案]C[解析]F=30N,n=3;物体做匀速直线运动,受平衡力,f=3F=3×30N=90N。故选
C.10、如图所示,滑轮重力和摩擦均不计,物体重均为100
N,与水平面间的摩擦力都是30
N,作用于各绳端的拉力分别为F1、F2、F3,要使物体做匀速直线运动,则下列说法中正确的是(
)A、
F1=100N、F2=50N、F3=200N
B、
F1=30N、F2=60N、F3=15N
C、
F1=100N、F2=50N、F3=50N
D、F1=30N、F2=15N、F3=60N
11、如图所示的装置处于平衡状态,若滑轮重和摩擦均不计,则G1、G2、G3的关系是( )A、2G1=G2=2
G3
B、G1=2G2=G3
C、G1=G2=G3
D、3G1=2G2=G3[答案]A12、滑轮重和摩擦忽略不计,体重为500N的人站在升降平台上拉绕过定滑轮的绳子,平台重100N,要使人和平台匀速向上运动,人拉绳的力应是多少?[答案]120N13、如图所示,物体A重80N,物体B重72N,物体A在物体B的作用下向右做匀速直线运动.如果在物体A上加一个水平向左的力,拉动物体A,使物体B以0.1m/s的速度匀速上升,则此时拉力F及3s内拉力F所做的功W分别是(已知动滑轮重18N,绳重以及绳与滑轮之间的摩擦不计)( )A、F=90N;W=27J
B、F=60N;W=54J
C、F=30N;W=27J
D、F=60N;W=18J[答案]B14、如图所示,一个质量60kg,底面积为0.1m2、高为0.1m的物块,通过滑轮组在25N拉力作用下以0.2m/s的速度作匀速直线运动.已知物块受到的滑动摩擦力为物重的0.1倍(g取10N/kg ).求:
(1)物体的密度是多少?
(2)拉力的功率是多少?
(3)该滑轮组的机械效率是多少?[答案]
(1)6×103kg/m3;(2)15W;(3)80%[解析](1)物体的密度ρ=m
V
=60kg
0.1m2×0.1m
=6×103kg/m3;(2)拉力的功率是P=F×3V=25N×3×0.2m/s=15W;(3)f=0.1G=0.1×mg=0.1×60kg×10N/Kg=60N;W有=fS;滑轮组绳子段数n=3W总=F×S2=F×3Sη=W有用
/W总
×100%=f
S/
F×3S
=60N
/25N×3
×100%=80%15、质量为60kg的小明利用如图所示滑轮组来提升重物.试思考并解答下列问题(g=10N/kg) 已知物重是800N,不考虑摩擦及绳重时,
(1)若实际拉力是500N,动滑轮的重力多大?
(2)小明利用此滑轮组至少需提起多重重物才能省力?
(3)小明利用此滑轮组至多能提起多重重物?[答案](1)200N;(2)200N;(3)1000N[解析](1)由图知,n=2,∵不考虑摩擦及绳重时,∴F=1/2(G+G动),∴G动=2F-G=2×500N-800N=200N;
(2)由题知,使用滑轮组省力时F<G,即1/2(G+G动)<G,∴G>G动=200N,即至少需提起200N重物才能省力;
(3)G人=m人g=60kg×10N/kg=600N,小明提起重物时F≤G人,即1/2(G+G动)≤G人,1/2(G+200N)≤600N,∴G≤1000N,
即:小明利用此滑轮组至多能提起1000N重物.16、用如图所示的滑轮组从15m深的水池中(水池面积很大,达几百平方米)提起底面积为200cm2,高2m的圆柱形实心物体,已知该物体的密度为2.5×103kg/m3,力F作用的绳子所能承受的最大拉力为350N,问:
(1)该物体所受的重力为多少牛?
(2)物体浸没水中时匀速拉动绳子,绳子自由端的拉力多少牛?(不计摩擦及滑轮重)
(3)物体以0.2m/s的速度匀速提起时,经多长时间绳子被拉断?(取g=10N/kg)[答案]
(1)1000N;(2)
300N;(3)67.5s.[解析](1)由题意知:圆柱体的底面积S=200cm2=2×10-2m2,高度h=2m,密度ρ=2.5×103kg/m3,g=10N/kg.所以圆柱体的体积:V=Sh=2×10-2m2×2m=4×10-2m3.圆柱体的质量:m=ρV=2.5×)103kg/m3×4×10-2m3=100kg
G=mg=100kg×10N/kg=1000N.(2)物体浸没在水中时,V排=V=4×10-2m3.此时受到的浮力:F浮=ρ水gV排=1×103kg/m3×10N/kg×4×10-2m3=400N,由于是n=2的滑轮组吊着圆柱体,所以绳子自由端的力F=1/2T,其中T为圆柱体对动滑轮的拉力.由图可知,T=G-F浮=1000N-400N=600N,所以绳子自由端的拉力F=1/2T=1/2
×600N=300N.(3)当绳子被拉断时,绳子受到的拉力F′=350N,动滑轮对圆柱体的拉力T′=2F′=700N,此时的浮力为:F浮′=G-T′=1000N-700N=300NV排′=F′浮/ρ水g
=300N/1×103kg/m3×
10Nkg
=0.03m3,物体浸入水中的长度h′为:h′=V排′/S
=0.03m3/0.02m2
=1.5m.物体上升的高度为:L=H-h′=15m-1.5m=13.5m,圆柱体运动的时间:t=L/v
=13.5m
0.2m/s
=67.5s.17.用相同的滑轮和绳子分别组成如图所示的甲、乙两个滑轮组,把相同的重物匀速提升相同的高度.若不计绳重及摩擦,下列说法正确的是( ) A.绳子受的拉力F1和F2大小相等,滑轮组的机械效率相同 B.绳子受的拉力F1和F2大小不相等,滑轮组的机械效率不同 C.绳子自由端移动的距离不相等,拉力对滑轮组所做的功相等 D.绳子自由端移动的距离不相等,拉力对滑轮组所做的功不相等解答:不计绳重及摩擦,∵拉力F=(G物+G轮),n1=2,n2=3,∴绳子受的拉力:F1=(G物+G轮),F2=(G物+G轮),∴F1≠F2,∵动滑轮重相同,提升的物体重和高度相同,W额=G轮h,W有用=G物h,∴利用滑轮组做的有用功相同、额外功相同,总功相同,∵η=×100%,∴滑轮组的机械效率相同,故A、B错;∵绳子自由端移动的距离s=nh,n1=2,n2=3,提升物体的高度h相同,∴s1=2h,s2=3h,∴s1≠s2,拉力做的功:W1=F1s1=(G物+G轮)×2h=(G物+G轮)hW2=F2s2=(G物+G轮)×3h=(G物+G轮)h∴,W1=W2,故C正确、D错.故选C.18.用一个定滑轮和一个动滑轮组成的滑轮组把重150N的物体匀速提升1m,不计摩擦和绳重,滑轮组的机械效率为60%.则下列选项错误的是( ) A.拉力一定是125NB.有用功一定是150J C.总功一定是250JD.动滑轮重一定是100N解答:对左图滑轮组,承担物重的绳子股数n=3,对物体做的有用功:W有=Gh=150N×1m=150J,∵η=,∴W总===250J,∴W额=W总﹣W有=250J﹣150J=100J;∵不计绳重和摩擦,W额=G轮h,∴动滑轮重:G轮===100N,拉力F的大小:F=(G物+G轮)=(150N+100N)=N;对右图滑轮组,承担物重的绳子股数n=2,对物体做的有用功:W有=Gh=150N×1m=150J,∵η=,∴W总===250J,∴W额=W总﹣W有=250J﹣150J=100J;∵不计绳重和摩擦,W额=G轮h,∴动滑轮重:G轮===100N,拉力F的大小:F=(G物+G轮)=(150N+100N)=125N.由以上计算可知,对物体做的有用功都是150J,总功都是250J,动滑轮重都是100N,故B、C、D都正确;但拉力不同,故A错.故选A.19.用如图所示的机械拉着重500N的物体在水平地面上匀速运动,物体受到的摩擦力为120N,绳子末端的水平拉力为50N,则滑轮组的机械效率为
;若物体运动的速度为0.2m/s,则10s内拉力做的功是
J.解答:(1)物体在水平地面上匀速运动,需要克服的是物体与地面间的摩擦力.机械效率η=;故答案为:80%.(2)10s内拉力作用点移动的距离S拉=nS物=3×0.2m/s×10s=6m,拉力所做的功W总=FS拉=50N×6m=300J;故答案为:300.20.如图,小王站在高3m、长6m的斜面上,将重200N的木箱沿斜面匀速从底端拉上顶端,拉力大小恒为120N,所花时间是10s.求:(1)木箱A沿斜面方向的运动速度.(2)小王对木箱做功的功率.(3)斜面的机械效率.解答:(1)v===0.6m/s;(2)W总=Fs=120N×6m=720J,P===72W;(3)W有用=Gh=200N×3m=600J,η==≈83.3%.答:(1)木箱A沿斜面方向的运动速度为0.6m/s.(2)小王对木箱做功的功率72W.(3)斜面的机械效率83.3%.21.小明在探究利用杠杆做功的实践活动中,将重G为15N的重物挂在杠杆的中点,用手竖直提起棒的另一端,使物体缓慢匀速提升,如图所示.(1)不计杠杆自身重力和摩擦,求拉力F的大小?(2)如杠杆是一根重为5N质量均匀的硬棒,若在2s内将重物提升0.l0m,则重物上升的速度是多大?小明使用杠杆所做的有用功为多大?机械效率是多大?解答:(1)由杠杆原理可知:FL1=GL2,即==,F==7.5N.(2)v===0.05m/s,W有用=Gh=15N×0.1m=1.5J,W额外=G杆h=5N×0.1m=0.5J,W总=W有用+W额外=1.5J+0.5J=2J,η===75%.答:(1)不计杠杆自身重力和摩擦,拉力F是7.5N.(2)重物上升的速度是0.05m/s;小明使用杠杆所做的有用功为1.5J.机械效率是75%.下次课预习
l1
l2
F2
F1
l1
F2
l2
A
B
F甲
F乙
乙
O
·
甲
O
·
B
A
·
·
年
级:
课
时
数:3课时学员姓名:
辅导科目:
学科教师:
教学主题
简单机械
授课日期及时段
教学过程
学习杠杆和滑轮相关知识阿基米德说过,给我一个支点,我可以撬起地球,你认为他的说法是否可行 1.杠杆:在力的作用下能绕固定点的硬棒叫做杠杆。2.杠杆的五要素支点:使杠杆绕着转动的固定点。动力:使杠杆转动的力。阻力:阻碍杠杆转动的力动力臂:从支点到动力作用线的垂直距离。阻力臂:从支点到阻力作用线的垂直距离。3.杠杆平衡:指杠杆保持静止状态或匀速转动状态4.研究杠杆的平衡(1).把杠杆的中央支在支架上,调节杠杆两端的螺母,使杠杆在水平位置处于平衡状态(便于直接在杠杆上测出力臂大小)。(2).在杠杆的两端分别挂上不同数量的钩码,在杠杆上左右移动钩码悬挂的位置,直到杠杆再次达到水平位置,处于平衡状态。(3).用直尺量出动力臂L1和阻力臂L2的大小。(4).动力与动力臂的乘积等于阻力与阻力臂的乘积5.杠杆平衡原理:动力×动力臂=阻力×阻力臂,即F1×L1=F2×L2杠杆的分类(1).L1>L2时,叫省力杠杆,其特点是省了力但费了距离。如开瓶盖的起子、铡刀、老虎钳、道钉撬等。(2).L1<L2时,叫费力杠杆,其特点是费了力但省了距离。如钓鱼杆、筷子、镊子、缝纫机脚踏板等。L1=L2时,叫等臂杠杆,其特点是不省力也不费力,不省距离也不费距离。如天平、定滑轮等。例1:画出渔民扳鱼网的杠杆示意图(图1)。 例2:一根扁担长1.4m,前后两筐内分别装有300N和400N的货物。问:人肩挑处离前筐多远才能平衡?(不计扁担及筐的质量)解:设前筐重力G1,肩到前筐距L1,
后筐重力G2,肩到后筐距L2。由G1L1=G2L2,即G1L1=G2(1.4m-L1),
答:
肩挑处应离前筐0.8m处,扁担平衡。例3:(2013 宜昌)下列杠杆属于费力杠杆的是( )A.用钓鱼杆钓鱼B.用起子开瓶盖C.用钳子剪钢丝D.用撬棒撬石头选A.例4:、下列所示的杠杆中,属于费力杠杆的是(D)例5:、下列关于力臂的说法中,正确的是(
B
)A、动力臂是指支点到动力作用点的距离B、阻力臂是指支点到阻力作用线的垂直距离C、动力臂与阻力臂之和等于杠杆长D、当力的作用线通过支点时,力臂最大例6:、下面举出的是几种根据杠杆原理制成的工具:A.钳子;B.铡刀;C.镊子;D.理发剪子;E.剪铁皮剪子;F.天平;G.定滑轮;H.起钉锤;I.指甲刀;J.起子;
K.缝纫机踏板.其中________是省力杠杆,________是费力杠杆,________等臂杠杆.
答案:ABEHIJ;
CDK
;FG
例7:、皮划艇是我国的奥运优势项目之一,比赛中,运动员一手支撑住浆柄的末端(视为支点),另一手用力划桨,此时的船桨是:(
B
)A.等臂杠杆
B.费力杠杆
C.省力杠杆
D.省功杠杆例8:园艺师傅使用如图所示的剪刀修剪树枝时,常把树枝尽量往剪刀轴O靠近,这样做的目的是为了:(
D
)A.增大阻力臂,减小动力移动的距离B.减小动力臂,减小动力移动的距离C.增大动力臂,省力D.减小阻力臂,省力例9:一个杠杆的动力臂与阻力臂之比为4∶1,则该杠杆是________杠杆,动力与阻力之比是________.若此杠杆受到的阻力是60
N,则当动力为________
N时,杠杆处于平衡状态.
答案:省力;1∶4
;15例10:如图所示为小明自制的风力板,口板为迎风板,其迎风面承受风力,b板为压重板,它水平放置,m为压重板上的铁板(a、b板重力不计)。当压重板上铁板重力一定时,风力大到一定程度,风力板就会倾倒,在这过程中,风对迎风板的作用力当作动力,_________当作阻力,压重板上的铁板越重,风力板倾倒时记录的风力越___________.小明通过查阅资料和实验,在压重板上加上重力不同的铁板,制成能测风力1~8级的8个风力板,构成一套风力探测仪。在南风盛行的某地,小明用这套风力探测仪测定当天最强的风力。(1)在开阔地的水平地面放置风力探测仪时,小明应____________________.(2)小明确定当天最强风力的方法是___________________________________答案:(铁板的)重力;大;
(1)将八个风力板的迎风面;
朝南放置;
(2)每天结束时,以倾倒风力板中记录风力最大的作当天最强风力。例11:实验台上有如下实验器材:一个带支架的杠杆、一个量程为0-5N的弹簧测力计、六个质量均为100g的钩码和两段细绳。请利用上述实验器材设计一个实验。证明“在杠杆平衡时,如果动力臂和阻力臂保持不变,则动力跟阻力成正比”。(1)在你所设计的实验中,如果用点A表示钩码作用在杠杆上的位置,用点B表示弹簧测力计作用在杠杆上的位置,请在图中的杠杆上标出A点和B点。(2)请写出主要实验步骤。
答案:(1)见右图(2)①用细绳做成两个绳套,分别拴牢在杠杆的A和B点处,调节杠杆使其在水平位置平衡。将弹簧测力计的指针调节到零刻度线位置。②在A点处依次挂1个、2个、3个、4个、5个、6个钩码,在B点处依次竖直向上拉弹簧测力计,分别使杠杆在水平位置平衡。将每次实验操作中挂在杠杆上的钩码的总质量和相应的弹簧测力计示数记录在表格中。例12:如图所示,绳子OO′悬吊着质量忽略不计的杆,在杆的a点挂上重物G,在O右侧某点b处挂上钩码.重物G的质量及a到O的距离不变,要使杆保持水平,b点挂的钩码个数(各个钩码质量相同)和b到O的距离的关系是图7中哪一幅图:(B)题型1:杠杆平衡原理公式的应用例1:如图所示,OA为一可绕O点转动的轻质杠杆,杆长2m,当作用于A点一个30N的竖直向上的力F时,为使杠杆水平不动,应将重力G=150N的重物悬吊于距A端多少m处。?0.4m题型2:杠杆平衡原理概念的理解例1:下列说法正确的是(
)A.支点到动力作用点的距离就是动力臂B.
动力臂和阻力臂不一定都在杠杆上C.动力臂和阻力臂的和一定等于杠杆的长度D.支点总是在动力作用点与阻力作用点之间答案:B题型3:杠杆平衡原理的实验探究例1:通过图甲乙丙实验可以验证同学们的猜想。
练一练(1)请设计一个简易实验,判断A、B的轻重.
所用器材:________________________________________
操作方法:________________________________________
现象及结论:________________________________________
(2)为进一步研究类似A、B轻重的问题,某同学在一根有等间距刻度的均匀杠杆两侧挂上每个质量都相等的钩码进行实验.杠杆静止于水平状态的三次实验情境如图所示。①根据图的实验,可以判断 _______同学的猜想是正确的(填“甲”、“乙”或“丙”)
②根据图的实验,该同学得出结论:只要满足“阻力×阻力作用点到支点的距离=动力×动力作用点到支点的距离”,杠杆就能平衡
a.这个结论是否正确?
b.用图所示的装置,怎样通过实验来说明该结论是否正确.
答案:
1:在“探究杠杆的平衡条件”的实验中:(1)所需的实验器材除了两端带有平衡螺母的杠杆、支架、细线、钩码外,还需要_________和__________。(2)张华同学发现杠杆的位置如图所示,则应将平衡螺母向________调节(选填“左”或“右”),使杠杆在_______位置平衡,这样做的目的是
。(3)接下来的实验过程中,张华同学同样使杠杆在
位置平衡,这样做的目的是___________________________________。(4)下列是某同学实验时记录的部分数据,请在空格处填上适当的数据:实验次数动力(N)动力臂(cm)阻力(N)阻力臂(cm)1346218129(5)某同学按照右图进行实验,发现F1·OA和F2·OB并不相等,这是由于___________________________________。答案:(1)弹簧测力计
刻度尺
(2)右
水平
消除杠杆自重对实验的影响
(3)水平
便于测量力臂
(4)2
6
(5)
OA不是F1的力臂2:如图,用测力计将长杆一端A微微抬离地面,测力计示数是F1;同理,用测力计将长杆的另一端B微微抬离地面,测力计示数是F2。则长杆的重力是(测力计保持竖直向上)(
)A.(F1+F2)/2
B.F1+F2
C.F1/F2
D.F1×F2答案:B3
如图(a)所示的杠杆是平衡的,在此杠杆支点两侧的物体下方分别加挂一个和钩码质量一样物体,如图(b)所示,那么,以下说法中正确的是(
)A.杠杆仍然平衡
B.杠杆可能平衡C.杠杆一定不能平衡,杠杆的B端下沉D.杠杆是否平衡与加挂物体的质量多少无关
1.杠杆一条件改变后杠杆将如何转动两边各加一个相等的力2.两边各减一个相等的力3.两边各加一个相等的力臂3.两边各减一个相等的力臂【思考1】如图所示,将体积相同的物体G1、G2分别挂在杠杆的两端,杠杆处于平衡状态。若将两个物体G1、G2同时减小相同的力,则(
)A.杠杆仍能保持平衡
B.杠杆不能平衡,A端下沉C.杠杆不能平衡,B端下沉
D.无法确定杠杆的状态【答案】
C【教学建议】推到这一类题型的结论【思考2】龟兔赛跑结束后,返回途中捡到半个大西瓜(如图),都想独吃,互不相让。争论的结果是:谁的体重大谁吃。可没有弹簧测力计怎么办?这时来了一只老山羊,知道情况后便说“这好办,你们两个各蹲在西瓜的一边,就可以看出哪个重些”。于是兔龟分别蹲到西瓜的一边,结果西瓜还在水平位置平衡如图.老山羊又说:“你们各自向中间移动相等的距离看看”,结果乌龟那边上翘了,兔子很高兴,说:“怎么样,还是我重吧!西瓜归我。”老山羊说:“不对,应该给乌龟。”请你用所学的杠杆知识分析,老山羊的话有道理吗?这个西瓜到底归谁?请用公式推导说出你的理由(西瓜的质量不计)。【答案】证明:设兔子的力臂为L1,重为G1,乌龟的力臂为L2,重为G2
第一次平衡,根据杠杆平衡原理,得G1L1=G2L2
(2分)
当向内移动L后,得
G1(L1-L)>G2(L2-L)
(2分)
即G1L1-G1L
>
G2L2-
G2L
G1L<
G2L
(1分)
得G1<
G2
(1分)
所以老山羊的话有道理
(G直接用m表示扣1分)杠杆中力的方向或杠杆移动后力的大小将如何改变【思考1】在研究杠杆平衡条件的实验中,某同学按图所示的装置来进行操作,他在杠杆的左端悬挂着一个物体,右端用弹簧测力计拉着,使杠杆在水平方向保持平衡,今用手拉着弹簧测力计缓慢地沿图中虚线自位置l移动至位置2,并保持杠杆始终在水平方向平衡,则弹簧测力计的读数
(
)
A.不断增大
B.不断减小
C.先增大后减小
D.先减小后增大【答案】
D【思考2】如图5所示,一根木棒AB在O点被悬挂起来,AO>OC,在A、C两点分别挂有两个和三个相同的钩码,木棒处于水平平衡。如在木棒的A、C两点各增加一个同样的钩码,则木棒(
)
A.绕O点顺时针方向转动B.绕O点逆时针方向转动C.仍保持平衡D.平衡被破坏,转动方向不定【答案】C3.转动时需要的力最小的类型【思考1】如图所示杠杆中,O是支点,在B端挂一个重物,为使杠杆平衡,要在A端加一个力。四个力中数值最小的力是(
)
A.
F1
B.
F2
C.
F3
D.
F4【答案】B【思考2】如图所示,要使杠杆处于平衡状态,在A点分别作用的四个力中,最小的是(
)A.F1
B.F2
C.F3
D.F4
【答案】C概念一、定滑轮:①定义:中间的轴固定不动的滑轮。②实质:定滑轮的实质是:
。③特点:使用定滑轮
。④对理想的定滑轮(不计轮轴间摩擦)F=G;实际生活中,F>G。绳子自由端移动距离SF
(或vF)=
二、动滑轮:①定义:和重物一起移动的滑轮。(可上下移动,也可左右移动)②实质:动滑轮的实质是:
。③特点:使用动滑轮能
。a.理想的动滑轮(不计轴间摩擦和动滑轮重力)则:F=
1
2G
只忽略轮轴间的摩擦则拉力F=
1
2(G物+G动)b.绳子自由端移动距离SF(或vF)=
注意:①可以省一半力,并不是说一定省力一半。a.理想的动滑轮(不计轴间摩擦和动滑轮重力),竖直拉绳最省力且省一半力即F1=
1
2G物;实际生活中,F1>
1
2G物.如图一:理想状态(不计轴间摩擦和动滑轮重力),F2
>F1=
1
2G物;实际生活中,F2
>F1>
1
2G物
。②可以省力,并不是只要用动滑轮就一定省力。如图二:a.理想的动滑轮(不计轴间摩擦和动滑轮重力)则
F=
2G物只忽略轮轴间的摩擦则拉力F=
2G物
+
G动b.绳子自由端移动距离SF(或vF)=
三、滑轮组的特点及其应用①滑轮组的特点:拉动物体时,既能省力又能改变力的方向②滑轮组的计算:使用滑轮组时,滑轮组用几段绳子吊着物体,提起物体所用的力就是动滑轮和重物总重的几分之一,动力作用点移动的距离就等于重物提升高度的几倍③根据一定的要求设计滑轮组绕线的方法:
a.滑轮组的绕线方法与绳子股数的确定滑轮组的绕线方法:常见滑轮组的构成有以下几种情况(如图所示),同一种构成有“定起”和“动起”两种绕线方法(绕线注意:绕线不交叉,不重叠;奇动偶定),要求绕线过程中绳子必须绷紧,具体绕线如图所示:b.绳子股数的确定:一般采用“切割法”定绳子股数,即从定滑轮和动滑轮之间切割(如上图),数出拴在动滑轮框上的绳子和最后从动滑轮引出的拉绳就是承担重物的绳子股数(图中的绳子股数已标出)c.计算:先根据题目中的条件,如绳子能承受的拉力和需要承担的物重计算出需要的绳子段数n(如果计算结果不是整数,一律进上去,例如,计算结果为3.2,则n取4)d.安装:n为偶数时,绳固定端固定在定滑轮上;反之n为奇数时,绳固定端要固定在动滑轮上.具体绕线时,一般先从固定端开始,按顺序由内向外绕,每个滑轮只能绕一次,绳不能相交叉.题型一、作图(用最小的力,应怎么绕线?)例1:
如图所示的甲、乙两个滑轮组,不计滑轮重.要求用最小的力将相同的重物拉起,应选用
滑轮组;请在你选用的滑轮组上画出绳子的绕法;如果物重100N,则用你选用的滑轮组及绕法,最小拉力为
N.[答案]甲;25.[解析]甲、乙两个滑轮组最省力的绕法分别如图甲有4段绳子拉重物,乙有3段绳子拉重物,根据F=G/n
知,甲更省力;则F=G/n
=100N/4
=25N.点评:正确给滑轮组绕绳是本题的基础,在不计绳重和摩擦的情况下,若有n股绳子在拉重物,则F=
G/n,所以n越大越省力,根据图中的滑轮组分别组装省力的情况,再进行比较并计算.例2:
要用最小的力将汽车拉动,试完成绳子的绕法.[解析]将绳子的一端固定在定滑轮的挂钩上,然后将绳子从内向外依次绕过每一只滑轮,共有4段绳子承担总的阻力.如图所示:例3:一个同学站在地面上,要利用如图所示的滑轮组提升重物.已知物重,而绳子最多只能承受的拉力.请你帮他在图中画出符合要求的绳子绕法.[解析]先判断.用“进一法”取.根据“奇拴动,一动配一定,变向加一定”原则,绳子应固定在动滑轮的钩上,由内向外绕.[答案]如图所示题型二、水平类a.
效率为100%
(滑轮组、摩擦力)例1:同一物体沿相同水平地面被匀速移动,如下图所示,拉力分别为F甲、F乙、F丙,不记滑轮与轻绳间的摩擦,比较它们的大小,则(
)
A、F甲<F乙<F丙
B、F甲>F乙>F丙
C、F甲>F乙=F丙
D、F甲=F乙>F丙[答案]B例2:如图所示,重600N的人站在重5400N的船上,通过滑轮把船匀速拉向岸边.人拉绳的力为500N,人和船相对静止.不计绳重和滑轮处摩擦,船受到水的阻力为( )A、500N
B、1000N
C、2500N
D、3000N[答案]
B[解析]因为船做匀速直线运动,所以,船受平衡力的作用,而人和船相对静止,因为F=500N,∴人的磨擦力是500N,方向向右,并且作用在船上,而该滑轮为定滑轮,∴绳子对船的拉力为500N,方向向右,而向右的拉力和船受到水的阻力是一对平衡力,所以,船受到水的阻力f=1000N.故选B.
例3:如图所示,物体A的质量是400g,物体B的体积是10cm3,此时A恰能沿着水平桌面向右做匀速直线运动.若将B始终浸没在水中,并使A沿着水平桌面向左做匀速直线运动时,需要施加0.95N水平向左的拉力.已知动滑轮重为0.3N,不计绳重以及绳和滑轮间的摩擦,则物体B重力为
N.(g取10N/kg)[答案]
0.7[解析]当物体A水平向右匀速运动时,分别对A、B物体受力分析如下图所示:
则根据力的平衡条件可得:f=F1,GB=2F1,f=1/2GB=----------------①
当A向左匀速直线运动时,分别对A、B物体受力分析如下图所示:
∵A物体对水平桌面的压力不变,接触面粗糙程度不变,∴f的大小不变,则根据力的平衡条件可得:F=f+F2,2F2+F浮=GB,
∴F-f=1/2(GB
-
F浮)------------②∵B物体始终浸没在水中,∴V排=V,∴F浮=ρ水gV------------③
由①②③式可得:GB=0.7N;
b.效率为100%
(滑轮组、摩擦力、功)例3:如图所示,置于水平桌面上的物体A重490N,物体B重294N,物体B在匀速下降了40cm的过程中,拉动物体A在水平桌面上匀速移动了一段距离;若用一水平向左的力F拉动物体A,使物体A在5s内匀速移动0.5m(不计动滑轮、绳重以及滑轮轮轴间摩擦),则下列说法正确的是
(
)A、拉力F为294N,拉力F的功率为29.4W
B、拉力F为147N,拉力F的功率为14.7W
C、物体A与桌面的滑动摩擦力为294N
D、绳子拉力对物体B所做的功为73.5J[答案]AD[解析]当A向右做匀速直线运动,水平方向上受到水平向右的拉力和向左的摩擦力,f=1
2
GB=1
2
×294N=147N;当A向左做匀速直线运动,水平方向上受到水平向左的拉力、向右的摩擦力、B对A的拉力;滑动摩擦力的大小跟压力大小和接触面的粗糙程度有关,压力不变,接触面的粗糙程度不变,摩擦力不变,所以向右的摩擦力为:f=147N.故C错误;A向左做匀速直线运动,受到平衡力的作用,A受到的水平向左的拉力为:F=f+GB
2
=147N+147N=294N;A的移动速度V=S
t
=0.5m
5s
=0.1m/s;拉力F的功率为P=FV=294N×0.1m/s=29.4W;故A正确;B错误;绳子拉力对物体B所做的功为W=GB
2
S=294N
2
×0.5m=73.5J,故D正确.故选AD.例4:如图所示,物体A的质量m
=12kg,在拉力F的作用下,物体A以0.1m/s的速度在水平面上做匀速直线运动,弹簧测力计的示数为12N,忽略滑轮与绳子的摩擦力以及滑轮、弹簧测力计和绳子所受的重力,并且绳子足够长。求:(1)物体A与水平面间摩擦力f的大小;(2)拉力F的大小;(3)物体A运动10s
的过程中,拉力F所做的功。(提示:拉力做功W2=Fs
,W2=W1,克服摩擦力做功W1=f
h)[答案]
(1)因做匀速直线运动,则:f=F示=12N(2)如图所示,作用在动滑轮轴上的拉力:F=2f=2×12N=24N(3)W=FS=24N×0.1m/s×10s×1/2=12J
[解析](1)因为物体A做匀速直线运动,所以物体受到绳子的拉力大小等于其所受摩擦力大小,而绳子拉力的大小由弹簧秤测出,所以f=12N
(2)由动滑轮的作用可知F=2f=2×12N=24N
(3)运动10秒钟,物体A通过的距离
S=v
t=0.1m/s×10s=1m
拉力F通过的距离S'=S/2=1m/2=0.5m
拉力F所做的功:W=
F
S'=24N×0.5m=12Jc.效率不为100%
(滑轮组、摩擦力、效率)例5:如右图所示,物体在水平面上做匀速直线运动,拉力F=60
N,该装置的机械效率为0.7,则物体受的摩擦力大小是(
)A、60
N
B、126
N
C、180
N
D、257.1
N[答案]B[解析]η=fh
FS
=fh
F×3h
=f
3F
;∴f=3Fη=3×60×70%N=126N.故选B.d.效率不为100%
(滑轮组、压强、机械效率)例5:用如图所示的滑轮组去拉物体A,已知A物质的密度是2
×103kg/m3,底面积是0.3m3,重力为600N。物体A在F=100N的拉力作用下,沿水平方向匀速前进了2m。(g取10N/kg)求:(1)物体A对水平地面的压强是多少
(2)物体A的体积是多大 (3)若该装置的机械效率为80%,物体A在水平方向上受到的阻力是多少?[答案](1)物体A对水平地面的压强是2×103.(2)
物体A的体积是0.03m3.(3)
物体A在水平方向上受到的阻力是160N.[解析](1)∵物体A在水平地面上作匀速直线运动,
∴F=G=600N,∴P=
F
/S=
600N/0.3m2=2×103Pa.(2)物A的质量m=
G/g
=
600N/10N/Kg=60Kg,物A的体积V=
m/ρ
=
60Kg
/2×103Kg/m3=0.03m3(3)拉力F所做的功W总=FS=100N×2×2m=400J,克服阻力所做的功W有=W总η=400J×80%=320J,物A所受阻力f=
W有/h=320J/2m=160N.题型三、竖直类a.
效率为100%(不计机械自重和摩擦)例1:如下图所示,用四个滑轮组分别匀速提升重力相同的物体,若不计滑轮重、绳重及摩擦,其中用力最小的是(
)
A.F1
B.F2
C.F3
D.F4
[答案]B例2:由两个动滑轮和两个定滑轮组成的滑轮组,站在地面的人用力向下拉绳,提起重为1000N的物体.问:(1)若不计摩擦和滑轮的重,所用拉力F是多大 (2)若实际所用拉力F为300N,则动滑轮总重是多少 (3)物体升高0.1m时,绳子的自由端所移动的距离是多少 [答案]
(1)250N;(2)200N;(3)0.4m[解析](1)因不计摩擦和滑轮的重量,所以拉力F=G/n=1000N/4=250N;(2)若实际所用拉力F为300N,则动滑轮总重G′=300×4N-1000N=200N;(3)物体升高0.1m时,绳子的自由端所移动的距离s=nh=4×0.1m=0.4m;
例3:如图所示,吊篮的重力为400N,动滑轮的重力为50N,定滑轮重力为40N,人的重力为600N,人在吊篮里拉着绳子不动时需用力(
)A.218N
B.220N
C.210N
D.236N[答案]C[解析]设人对绳的拉力F,将人、吊篮和动滑轮视为一个整体,此时整体处于静止状态,整体重力由5段绳子承担,所以有5F=.所以b.效率不为100%
(滑轮组、机械效率)例4:
用一个动滑轮、一个定滑轮组成的滑轮组来匀速提升重物G,如图所示,已知物重G=600N,拉力F=250N,求10秒内将重物升高0.5m的过程中,所做的有用功,额外功,及拉力的功率为多大?若所提升重物重力为750N,拉力为多大?(不计绳重和摩擦力).[答案]
所做的有用功为300J,额外功为75J,拉力的功率为37.5W,若所提升重物重力为750N,拉力为300N.[解析](1)由图可知,n=3,绳子自由端移动的距离s=nh=3×0.5m=1.5m,有用功W有=Gh=600N×0.5m=300J,总功W总=Fs=250N×1.5m=375J,额外功W额=W总-W有=375J-300J=75J;P总=W总
t
=375J
10s
=37.5W;(2)∵F=1
n
(G+G动),∴G动=3F-G=3×250N-600N=150N,∴所提升重物重力为750N,拉力F′=1
3
(G′+G动)=1
3
×(750N+150N)=300N.例5:建筑工人用如图所示的装置把重400N的物体匀速提升3m.所用的手拉力为300N.则该工人所做的有用功为
J,总功为
J,该滑轮组的机械效率是
(保留三位有效数字).若用该装置提升500N的重物,此时滑轮组的机械教率将
(填“变大”、“变小”或“不变”)[答案]
1200,1800,66.7%,变大[解析]由图知,有2段绳子承担物重,若重物提升h=3m,绳子末端移动距离s=2h=2×3m=6m.拉力做的有用功:W有用=Gh=400N×3m=1200J;拉力做的总功:W总=Fs=300N×6m=1800J.该机械的效率:η=W有用
W总
=1200J
1800J
≈66.7%.当提升重物的重力增加,做的有用功就变大,而额外功几乎不变,故机械效率变大.c.
效率不为100%
(滑轮组、功率、机械效率)例6:在小型建筑工地,常用简易的起重设备竖直吊运建筑材料,其工作原理相当于如图所示的滑轮组。某次将总重G为4000
N的砖块匀速吊运到高为10
m的楼上,用时40
s,卷扬机提供的拉力F为2500
N。求在此过程中:(1)有用功;(2)拉力F的功和功率;(3)滑轮组的机械效率。[答案]
(1
)4
×104J;(2
)5
×104J,1.25×103w;(3)80%[解析](1
)W有=Gh=4000N×10m=4
×104J
(2
)W总=Fs=F
×2h=2500N×2×10m=5
×104J,P=W/S=FV=5
×104J/40s=1.25×103w.(3)η=
W有/
W总=80%。d.效率不为100%
(滑轮组、浮力、机械效率)例7:如图所示,重物A是体积为10dm3,密度为7.9
×103
kg/m3的实心金属块,将它完全浸没在水中,始终未提出水面。若不计摩擦和动滑轮重,要保持平衡,求:(1)作用于绳端的拉力F是多少?(2)若缓慢将重物A提升2m,拉力做的功是多少?(3)若实际所用拉力为400N,此时该滑轮的效率是多少?(g=10N/kg)[答案]
172.5N;1380J;43.1%[解析](1)物体A的体积为V=10dm3=0.01m3,则完全浸没在水中时,V排=V=0.01m3,金属块受到的浮力:F浮=ρ水gV排=ρ水gV=1×103kg/m3×10N/kg×0.01m3=100N;金属块的重力:G=mg=ρVg=7.9×103kg/m3×0.01m3×10N/kg=790N,∵由图可知,动滑轮是由4股绳子承担,在不计摩擦和动滑轮重的条件下,∴作用于绳端的拉力:F=1/4(G-F浮)=1/4(790N-100N)=172.5N.(2)若缓慢将重物A提升2m,因为n=4,所以s=nh=4×2m=8m,拉力做的功:W=Fs=172.5N×8m=1380J.(3)若实际所用拉力为400N,则总功为:W总=Fs=400N×8m=3200J;使用滑轮组所做的有用功:W有用=(G-F浮)h=(790N-100N)×2m=1380J,此时该滑轮的效率此时该滑轮的效率:η=W有用
W总
×100%=1380J
/3200J
×100%≈43.1%.1.有用功:为达到目的必须做的功;额外功:为了达到目的并非需要又不得不做的功;总功:有用功和额外功的总和。
机械效率的计算:对于滑轮组而言的公式运用(不可直接用):;对于水平方向上的滑轮组及滑轮组与浮力组合、与斜面组合时,可牢记针对滑轮组的机械效率,力均是作用在滑轮组上的,进行受力分析找力并求该力所作的功,分清有用功和总功,运用基本公式求机械效率。
3.提高机械效率的方法:由公式可知,当有用功一定时,额外功越小,机械效率越高,因此设法减小额外功可以提高机械效率。如减轻动滑轮本身的重量,加润滑油可以减小摩擦等;当额外功一定时,有用功越大,机械效率越高,因此增大有用功可以提高机械效率,如增加物重可以提高机械效率。机械效率具有“可变性”。由可知,如果该机械的额外功(W额外)一定,有用功()越大,机械效率越大。因此,增加物重能增大机械效率。由上面的公式还可以知道:当有用功一定时,额外功越小,则机械功率越大。因此设法减小额外功可以提高机械功率。如减轻机械本身的重量,加润滑油以减少摩擦,都可以不同程度地减少额外功,提高机械效率。
4.与斜面效率有关的公式:
;;;根据,可知,利用这个式子可求物体与斜面间的摩擦力。斜面机械效率与斜面的坡度有关,坡度越大,物体与斜面间压力越小,滑动摩擦力越小,提升相同高度,物体走过的路程越短,因此克服摩擦做的额外功越小,机械效率越大。5.杠杆机械效率:6.组合机械的机械效率:1、机械效率的认识和比较1.甲吊车比乙吊车的机械效率高,当它们分别把相同质量的物体匀速提升相同高度时,则( ) A.甲吊车的电动机做的有用功较多 B.乙吊车的电动机做的额外功较多 C.甲吊车的电动机做的总功较多 D.甲、乙两吊车的电动机做的总功相同解答:A、分析知甲乙吊车做的有用功相同.此选项错误,不符合题意;B、两辆吊车做的有用功相同,乙吊车做的额外功较多,所以乙的效率较低.此选项正确,符合题意;C、已知甲吊车的机械效率高,有用功相同,如果甲吊车的总功较多就与效率高矛盾.此选项错误,不符合题意;D、两吊车做的有用功相同,如果总功也相同,则机械效率相同.此选项错误,不符合题意.故选B.2.下列关于机械效率的说法正确的是( ) A.机械效率不可能达到100% B.随着科学技术的发展,机械效率可能会大于100% C.滑轮组的机械效率一定大于动滑轮的机械效率 D.杠杆的机械效率一定大于动滑轮的机械效率解答:AB、科技无论怎么发展,机械元件之间摩擦都不能消除,机械效率不可能达到100%,更不会大于100%.所以选项A正确,选项B错误.CD、滑轮组的机械效率、动滑轮的机械效率、杠杆的机械效率高低,跟机械的重、提起物体的重、摩擦、绳重等有关,在这些不能确定的情况下不能确定哪种机械的机械效率的更大一些.选项CD都错误.故选A.3.如图所示,小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,用甲滑轮所做的总功为W1,机械效率为η1;用乙滑轮所做的总功为W2,机械效率为η2.若不计绳重与摩擦,则( ) A.W1=W2,η1=η2B.W1=W2,η1<η2C.W1<W2,η1>η2D.W1>W2,η1<η2解答:因为小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,所以两种情况的有用功相同;当有用功一定时,利用机械时做的额外功越少,则总功越少,机械效率越高.又因乙滑轮是动滑轮,所以利用乙滑轮做的额外功多,则总功越多,机械效率越低.即W1<W2,η1>η2,所以C选项正确.故选C.4.在不计摩擦和绳子质量的情况下,分别使用定滑轮、动滑轮、滑轮组(两个定滑轮和两个动滑轮)匀速提升同一物体到同一高度处,其机械效率分别为η定、η动、η组,则下列选项正确的是( ) A.η组<η动<η定B.η定<η动<η组C.η动<η定<η组D.η定<η组<η动解答:∵匀速提升同一物体到同一高度处,∴三种情况下做的有用功相同,大小都为W有用;∵不计绳子质量和摩擦,∴使用滑轮做的额外功:W额=G轮h,又∵使用定滑轮、动滑轮、滑轮组的动滑轮的个数为0、1、2,∴使用定滑轮、动滑轮、滑轮组做的额外功:W额1<W额2<W额3,∵W总=W有用+W额,∴三种情况下做的总功:W定<W动<W组,∵η=,∴使用定滑轮、动滑轮、滑轮组的机械效率:η定>η动>η组.故选A.滑轮组的机械效率1.如图所示,不计摩擦,把重G=16N的物体匀速提起所用的拉力F=10N,则关于该动滑轮的说法中错误的是( ) A.动滑轮重4N B.使该用动滑轮要费距离 C.该动滑轮的机械效率为80% D.提升物体的速度越快,机械效率越高解答:A、根据F=(G物+G动)得G动=2F﹣G物=2×10N﹣16N=4N,所以A正确.B、动滑轮可以省一半的力,但费距离.所以B正确.C、η=×100%=×100%=×100%=80%,所以C正确.D、提升物体的速度快,则做功快,功率大,但效率不变.所以D错误.故选D.2.如图所示,小丽用滑轮组匀速提升一个重为600N的物体,物体上升的速度为0.1m/s,人拉绳的力F为250N,不计绳重和摩擦,下列说法不正确的是( ) A.人拉绳做功的功率为75WB.滑轮组的机械效率为80% C.绳子自由端移动的速度为0.3
m/sD.动滑轮重为100N解答:∵物体上升的速度v=0.1m/s,n=3∴v′=3v=3×0.1m/s=0.3m/s;故C正确;人拉绳做功的功率P===Fv′=250N×0.3m/s=75W,故A正确;滑轮组的机械效率:η=====80%;故B正确;∵F=(G物+G轮)即250N=(600N+G轮)G轮=150N,故D错误.故选D.3.如图所示,利用轻质滑轮组匀速拉动水平地面上重为300N的物体,拉力F的大小为30N.若物体和地面之间的摩擦力大小为45N,则A处的拉力大小和滑轮组的机械效率分别为( ) A.45N、50%B.45N、75%C.60N、50%D.60N、75%解答:①物体在水平地面上做匀速运动,则此时A处绳子的拉力与物体与地面之间的摩擦力是一对平衡力,∵物体和地面之间摩擦力为f=45N,∴A处的拉力大小为FA=f=45N.②从图可知,由2段绳子与动滑轮相连,则S=2s物,∵F=30N,f=45N,∴滑轮组的机械效率为:η======75%.故选B.4.小明用如图所示滑轮组将一个放在水平地面上的物体匀速拉动,物体移动了3m,物体重为2000N,与地面的接触面积为0.5m2,运动过程中物体受到的摩擦力为450N,绳子自由端受到的拉力F
为200N,求:(1)物体对地面的压强;(2)拉力F做的功;(3)该装置的机械效率.解答:(1)物体对地面的压力:F=G=2000N,物体对地面的压强:p===4000Pa;(2)由图可知:n=3,绳子自由端移动的距离:s=ns′=3×3m=9m,拉力F做的功:WF=F拉s=200N×9m=1800J;(3)该装置的机械效率:η=×100%=×100%=×100%=×100%=×100%=75%.答:(1)物体对地面的压强为4000Pa;(2)拉力F做的功为1800J;(3)该装置的机械效率为75%.5.中华神州打捞公司用如图所示的滑轮组,打捞沉在长江三峡江底一个方形物体.物体上表面距离水面50米,重力为2400N,体积为0.2m3.打捞时匀速提升该物体.(g=10N/kg
ρ水=1.0×103kg/m3)
求:①物体沉在江底时,上表面受到的水的压强;②物体在露出水面之前受到水的浮力;③物体在露出水面之前,人的水平拉力F【设物体在露出水面之前此装置的机械效率为80%】解答:(1)物体上表面受到的压强为P=ρgh=1.0×103kg/m3×10N/kg×50m=5×105Pa;(2)物体露出水面前受到的浮力为F浮=ρ液gV排=1.0×103kg/m3×10N/kg×0.2m3=2000N;(3)物体出水前,滑轮组对物体的拉力为F′=G﹣F浮=2400N﹣2000N=400N作用在绳子末端的拉力为F===250N.答:(1)物体上表面受到的压强为5×105Pa;(2)物体露出水面前受到的浮力为2000N;(3)物体出水前,作用在绳子末端的拉力为250N.斜面的机械效率1.如图甲所示,王大叔正吃力地把一重物送往高台,放学回家的小鹏看见后急忙前去帮忙.他找来一块木板,搭成图乙所示的斜面,结果非常轻松地把重物推到了高台上.关于这两种方法,下列说法中正确的是( ) A.王大叔克服重力做功较多B.两人做同样多的有用功 C.小鹏做功的功率要大些D.甲、乙两种情况下的机械效率一样解答:A、B、这两种方法,都把重物推到了高台上,两人做同样多的有用功,克服重力做功相同.选项A错误、选项B正确;C、功率等于功与时间是比值,由于题中没有给出时间,不能确定哪个做功的功率大.此选项错误;D、由于乙中情况需要克服摩擦做功,所以乙种情况下的机械效率小.此选项错误.故选B.2.如图,某同学用F=300N的力将重为400N的物体从斜面底端匀速拉到顶端,斜面的高为3m,底边为4m,斜面的机械效率( ) A.93.75%B.80%C.56.25%D.45%解答:有用功:W有用=Gh=400N×3m=1200J,斜面高3m,斜面底边是4m,所以斜面长度为:s==5m,总功:W总=Fs=300N×5m=1500J,机械效率:η===80%.故选B.3.如图所示,斜面长为3m,高为lm,工人用400N沿斜面方向的力将重为840N的箱子推到车上.在这过程中( ) A.有用功是400J,总功是840JB.有用功是840J,额外功是400J C.总功是12O0J,机械效率是7O%D.有用功是400J,机械效率是7O%解答:对木箱做的有用功:W有=Gh=840N×1m=840J,利用斜面做的总功:W总=Fs=400N×3m=1200J;额外功W额=W总﹣W有用=1200J﹣840J=360J,斜面效率:η==×100%=70%.故选C.4.一个重为G的物体沿如图所示的左右两个斜面,被推上同一个平台,左斜面长为L1,是右斜面长L2的1/2,且沿两个斜面推动物体时所受摩擦力一样大,那么两个斜面相比( ) A.用左斜面省力少,机械效率比右高 B.用右斜面省力多,机械效率比左高 C.两个斜面做的有用功一样,效率也一样 D.条件不足,无法判断解答:∵左斜面倾斜角度大于右斜面,∴用右斜面更省力;由题知,沿两个斜面推动物体时所受摩擦力一样大,f1=f2,L1<L2,∵W额=fL,∴利用两个斜面做额外功:W额1<W额2,∵W有用=Gh,G、h相同,∴利用两个斜面做的有用功:W有用1=W有用2,∵W总=W有用+W额,∴利用两个斜面做的总功:W总1<W总2,∵η=,∴利用两个斜面的效率η1>η2.由上述分析可知,用左斜面省力少,机械效率比右高.故选A.5.如图所示,斜面长6m,高3m,用沿斜面向上、大小为100N的拉力F使物体在5s内沿斜面移动了2m,下列说法正确的是( ) A.滑轮组的机械效率是40%B.物体重300N C.拉力F做的功是600JD.拉力F的功率是40W解答:因条件不足,无法计算物体重和机械效率,故A、B错.拉力F移动的距离:s=3s′=3×2m=6m;拉力F所做的总功:W总=Fs=100N×6m=600J,故C正确;拉力F做功的功率:P===120W,故D错;故选C.思考:若物体的重力为300N,整个装置的机械效率为多少?物体所受摩擦力为多大?滑轮组机械效率能求出吗?杠杆的机械效率1.小明在探究利用杠杆做功的实践活动中,所用的杠杆是一根质量均匀、重为5N的硬棒,他将棒的一端固定,把重为15N的物体挂在棒的中点,然后用手缓慢竖直向上提起棒的另一端,如图所示,若把物体提升了10cm,则小明作用在杠杆上的拉力是
N,此过程中杠杆的机械效率是
.解答:15N的物体和5N杠杆的重作用在杠杆中点上,动力竖直作用在杠杆的末端,动力臂是阻力臂的2倍,所以动力是阻力的二分之一,所以F=(G+G杆)=(15N+5N)=10N.使用任何机械都不省功,动力是阻力的二分之一,动力移动的距离是阻力移动距离的2倍,有用功:W有=Gh=15N×h,总功:W总=Fs=10N×2h,机械效率:η===75%.故答案为:10;75%.2.如图所示,用竖直向上的力匀速拉动较长的杠杆,使重为18N的物体缓慢升高0.1m,拉力大小F=8N,拉力移动的距离为0.25m.拉力所做的功为
J,有用功为
J,杠杆的机械效率为
%.解答:有用功为W有=Gh=18N×0.1m=1.8J;拉力所做的功为W总=Fs=8N×0.25m=2J,杠杆的机械效率为η=×100%=×100%=90%.故答案为:2;1.8;90.机械效率相关实验1.小红在探究“影响滑轮组机械效率高低的因素”时,提出下列假设:(1)机械效率可能跟动滑轮有关(2)机械效率可能跟被拉物体上升的高度有关(3)机械效率可能跟被拉物体重有关(4)机械效率可能跟承受绳子的段数有关然后小婷设计了如图所示的2组实验进行对比,来验证小红提出的假设,则该实验验证的假设是( ) A.(1)B.(2)C.(3)D.(4)解答:猜想滑轮组机械效率可能跟动滑轮、物体上升的高度、物体重力、绳子的段数有关,探究滑轮组机械效率跟其中一个因素的关系时,控制其它因素不变.如图,动滑轮、物体上升的高度、物体重力可以相同,绳子的段数不同,所以如图探究滑轮组机械效率跟承受绳子的段数的关系.故选D.2.在“测定动滑轮机械效率”的实验中,小明用如图所示的动滑轮提升钩码,改变钩码的数量,正确操作,实验数据如下:实验序号钩码重钩码上升的高度h/cm拉力F/N绳端移动的距离s/cm①1.020.000.740.00②2.020.001.240.00③3.020.001.740.00(1)实验时,用手
拉动弹簧测力计,使持在动滑轮下的钩码缓缓上升.(2)第①次实验时测得动滑轮的机械效率为
.(3)第③次实验时,钩码上升的速度为0.05m/s,则拉力的功率为
W.(4)由表中实验数据分析可知,同一动滑轮,所提升物重增大,机械效率将
(选填“增大”、“减小”或“不变”).解答:(1)在实验时,应用手匀速拉动弹簧测力计,使挂在动滑轮下的钩码缓缓上升.(2)η1=×100=×100%≈71.4%(3)由第三次数据知,s=2h,所以绳子移动速度为物体上升速度的2倍.P总===Fv=1.7N×0.05m/s×2=0.17W(4)根据表格中数据,②的效率η2=×100%=×100%≈83.3%η3=×100%=×100%≈88.2%根据三次的机械效率及物重的变化可得同一动滑轮,所提升物重增大,机械效率将增大.故答案为:(1)匀速;(2)71.4%;(3)0.17;(4)增大.3.斜面是一种简单机械,生活中人们常常利用它来省力.小明想搽究“斜面的机械效率与斜面的倾斜程度的关系”.于是他找来木块A、长木扳B、三个高度不同的长方体C和一把弹簧测力计进行实验,实验装置如图所示.(1)除上述器材外,小明要完成实验还需要的一种器
材是
;(2)在实验过程中,应沿斜面向上拉动术块,使木块做
运动;(3)实验记录数据如下表,则第3次实验时斜面的机械效率为
;(4)分析比较下表中的实验数据,可得到的结论是:斜面越陡
.实验次数斜面倾斜程度木块重G/N斜面高度h/m沿斜面的拉力F/N木块沿斜面移动的距离S/m斜面的机械效率1较缓50.23.30.560.6%2较陡50.253.80.565.8%3最陡50.34.20.5解答:(1)要测量斜面的高度和木块沿斜面移动的距离就要使用长度的测量工具﹣﹣﹣刻度尺;(2)为了保证弹簧测力计的示数稳定,就要让木块做匀速直线运动;(3)第三次实验时,斜面的机械效率η==≈71.4%;(4)由图中数据可知:斜面的倾斜程度越大,斜面的机械效率越高.故答案为:(1)刻度尺;(2)匀速直线;(3)71.4%;(4)斜面的机械效率越高.4.用如图所示的实验装置测量杠杆的机械效率.实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升.(1)实验中,将杠杆拉至图中虚线位置,读出测力计的示数F为
N,钩码总重量G为1.0N,钩码上升高度h为0.1m,测力计移动距离s为0.3m,则杠杆的机械效率为
%.(2)为了进一步研究杠杆的机械效率与哪些因素有关,一位同学用该实验装置,先后将钩码挂在A、B两点,测量并计算得到下表所示的两组数据:次数钩码悬挂点钩码总重G/N钩码移动距离h/m拉力F/N测力计移动距离s/m机械效率η/%1A点1.50.100.70.3071.42B点2.00.151.20.3083.3根据表中数据,能否得出“杠杆的机械效率与所挂钩码的重有关,钩码越重其效率越高”的结论?答:
;请简要说明理由(写出一条即可):
.解答:(1)由图可知,弹簧测力计的分度值是0.1N,所以它的示数是0.5N;在实验过程中,有用功是:W有用=Gh=1.0N×0.1m=0.1J,总功是:W总=Fs=0.5N×0.3m=0.15J,所以杠杆的机械效率是:η=×100%=×100%=66.7%.(2)分析机械效率的影响因素应采取控制变量法,研究提起的物重和机械效率的关系时,应保持钩码所挂位置不变,而实验中,两次钩码悬挂的位置是不同的;同时,还应进行多次实验,分析多组数据,才能得出有说服力的正确结论,只凭一次实验数据做出结论是不科学的.故答案为:(1)0.5;
66.7;(2)不能.两次实验时,钩码没有挂在同一位置,同时改变两组条件,数据不宜直接比较(或仅根据一次对比实验所得结论是不可靠的).(此环节设计时间在10分钟内)(以学生自我总结为主,TR根据教案中的总结进行引导为辅,为本次课做一个总结回顾;总结方式可以多种多样,如画思维导图、默想回忆、抢答形式等。教案中给到重难点/易错点等的总结条目。)1.
2.3.1.
包含预习下次课内容和复习本次课内容两部分;
2.
建议作业量不宜过多,最好控制在学生30分钟内能够完成;3.
每节课前教师对作业进行批改与讲解;本次课复习1.如图所示,轻质木杆AB可以绕O点转动,OA的长度是OB的三倍,A端细线下所挂280N的重物静止在水平地面上,在B点用600N的动力竖直向下拉动,木杆静止不动,则重物对水平地面的压力为
N,此木杆为
(填“省力”
“费力”或“等臂”)杠杆。答案:80;费力2.
如图所示,—根铁棒在水平拉力F的作用下,以O点为转轴,由竖直位置逆时针匀速转向水平位置的过程中,动力F与动力臂L的大小变化是A.F增大,L增大
B.F减小,L减小
C.F增大,L减小
D.F减小,L增大答案:C3.(2011年中考·浙江义乌卷)如图所示,一块厚度、密度均匀的长方形水泥板放在水平地面上,用一竖直向上的力,欲使其一端抬离地面,则(
)A.F甲>F乙,因为甲方法的动力臂长
B.F甲
D.F甲=F乙,因为动力臂都是阻力臂的2倍答案:D
4.如图所示,长度为2L的轻质细杆可在竖直面内绕竖直墙壁上的固定转轴O无摩擦地转动.AB为一段长度为1.5L的不可伸长的轻绳,绳AB能承受的最大拉力为F,现将绳的两端AB分别与墙壁及杆相连,使杆始终保持水平.则杆的末端C处可悬挂重物的最大重力为
.答案:3F/85.如图所示,轻质杠杆OA中点悬挂重为60N的物体,在A端施加一竖直向上的力F,杠杆在水平位置平衡,则力F的大小是_______________,保持F的方向不变,将杠杆从A位置匀速提升到B位置的过程中,力F将_____________(选填“变大”、“变小”或“不变”)。答案:30N;不变6.如图甲所示,小明在探究“杠杆的平衡条件”实验中所用的实验器材有:杠杆、支架、弹簧测力计、刻度尺、细线和质量相同的钩码若干个。(1)实验前,将杠杆中点置于支架上,当杠杆静止时,发现杠杆右端下沉。此时,应把杠杆两端的平衡螺母向 (选填“左”或“右”)调节,使杠杆在不挂钩码时,保持
并静止,达到平衡状态。这样做的好处是:便于在杠杆上直接测量
。(2)杠杆调节平衡后,小明在杠杆上A点处挂4个钩码,在B点处挂6个钩码杠杆恰好在原位置平衡。于是小明便得出了杠杆的平衡条件为: 。他这样得出的结论是否合理? ;为什么? 。(3)实验结束后,小明提出了新的探究问题:“若支点不在杠杆的中点时,杠杆的平衡条件是否仍然成立?”于是小组同学利用如图乙所示装置进行探究,发现在杠杆左端的不同位置,用弹簧测力计竖直向上拉使杠杆处于平衡状态时,测出的拉力大小都与杠杆平衡条件不相符。其原因是:
。答案:(1)左;水平;力臂
(2)F1
l1=
F2
l2;不合理;结论具有偶然性(结论没有普遍性)(3)杠杆自重的影响。7.如图所示,重500N的人站在重2500N的船上,用滑轮组把船匀速拉向岸边,人和船相对静止..不计绳重和滑轮轴摩擦,人拉绳的力为300N,求船受到水的阻力为(
)A、900N
B、450N
C、1100N
D、2700N8、如图中的水平桌面足够长,不计托盘质量和滑轮与绳的摩擦.物体A重10N,当物体B重为2N时,物体A保持静止,这时A物体受到的摩擦力为
N;当物体B重为3N时,物体A向右做匀速直线运动,运动一段时间托盘着地,此后物体继续运动一段时间,此时物体A受到的摩擦力是
N.方向是
.[答案]
2;3;水平向左.
9、如图所示,船和人总重1500N,船上的人用力F=30N的拉力拉绳,船作匀速直线运动,则船受到水的阻力为( )
A.30NB.60NC.90ND.500N[答案]C[解析]F=30N,n=3;物体做匀速直线运动,受平衡力,f=3F=3×30N=90N。故选
C.10、如图所示,滑轮重力和摩擦均不计,物体重均为100
N,与水平面间的摩擦力都是30
N,作用于各绳端的拉力分别为F1、F2、F3,要使物体做匀速直线运动,则下列说法中正确的是(
)A、
F1=100N、F2=50N、F3=200N
B、
F1=30N、F2=60N、F3=15N
C、
F1=100N、F2=50N、F3=50N
D、F1=30N、F2=15N、F3=60N
11、如图所示的装置处于平衡状态,若滑轮重和摩擦均不计,则G1、G2、G3的关系是( )A、2G1=G2=2
G3
B、G1=2G2=G3
C、G1=G2=G3
D、3G1=2G2=G3[答案]A12、滑轮重和摩擦忽略不计,体重为500N的人站在升降平台上拉绕过定滑轮的绳子,平台重100N,要使人和平台匀速向上运动,人拉绳的力应是多少?[答案]120N13、如图所示,物体A重80N,物体B重72N,物体A在物体B的作用下向右做匀速直线运动.如果在物体A上加一个水平向左的力,拉动物体A,使物体B以0.1m/s的速度匀速上升,则此时拉力F及3s内拉力F所做的功W分别是(已知动滑轮重18N,绳重以及绳与滑轮之间的摩擦不计)( )A、F=90N;W=27J
B、F=60N;W=54J
C、F=30N;W=27J
D、F=60N;W=18J[答案]B14、如图所示,一个质量60kg,底面积为0.1m2、高为0.1m的物块,通过滑轮组在25N拉力作用下以0.2m/s的速度作匀速直线运动.已知物块受到的滑动摩擦力为物重的0.1倍(g取10N/kg ).求:
(1)物体的密度是多少?
(2)拉力的功率是多少?
(3)该滑轮组的机械效率是多少?[答案]
(1)6×103kg/m3;(2)15W;(3)80%[解析](1)物体的密度ρ=m
V
=60kg
0.1m2×0.1m
=6×103kg/m3;(2)拉力的功率是P=F×3V=25N×3×0.2m/s=15W;(3)f=0.1G=0.1×mg=0.1×60kg×10N/Kg=60N;W有=fS;滑轮组绳子段数n=3W总=F×S2=F×3Sη=W有用
/W总
×100%=f
S/
F×3S
=60N
/25N×3
×100%=80%15、质量为60kg的小明利用如图所示滑轮组来提升重物.试思考并解答下列问题(g=10N/kg) 已知物重是800N,不考虑摩擦及绳重时,
(1)若实际拉力是500N,动滑轮的重力多大?
(2)小明利用此滑轮组至少需提起多重重物才能省力?
(3)小明利用此滑轮组至多能提起多重重物?[答案](1)200N;(2)200N;(3)1000N[解析](1)由图知,n=2,∵不考虑摩擦及绳重时,∴F=1/2(G+G动),∴G动=2F-G=2×500N-800N=200N;
(2)由题知,使用滑轮组省力时F<G,即1/2(G+G动)<G,∴G>G动=200N,即至少需提起200N重物才能省力;
(3)G人=m人g=60kg×10N/kg=600N,小明提起重物时F≤G人,即1/2(G+G动)≤G人,1/2(G+200N)≤600N,∴G≤1000N,
即:小明利用此滑轮组至多能提起1000N重物.16、用如图所示的滑轮组从15m深的水池中(水池面积很大,达几百平方米)提起底面积为200cm2,高2m的圆柱形实心物体,已知该物体的密度为2.5×103kg/m3,力F作用的绳子所能承受的最大拉力为350N,问:
(1)该物体所受的重力为多少牛?
(2)物体浸没水中时匀速拉动绳子,绳子自由端的拉力多少牛?(不计摩擦及滑轮重)
(3)物体以0.2m/s的速度匀速提起时,经多长时间绳子被拉断?(取g=10N/kg)[答案]
(1)1000N;(2)
300N;(3)67.5s.[解析](1)由题意知:圆柱体的底面积S=200cm2=2×10-2m2,高度h=2m,密度ρ=2.5×103kg/m3,g=10N/kg.所以圆柱体的体积:V=Sh=2×10-2m2×2m=4×10-2m3.圆柱体的质量:m=ρV=2.5×)103kg/m3×4×10-2m3=100kg
G=mg=100kg×10N/kg=1000N.(2)物体浸没在水中时,V排=V=4×10-2m3.此时受到的浮力:F浮=ρ水gV排=1×103kg/m3×10N/kg×4×10-2m3=400N,由于是n=2的滑轮组吊着圆柱体,所以绳子自由端的力F=1/2T,其中T为圆柱体对动滑轮的拉力.由图可知,T=G-F浮=1000N-400N=600N,所以绳子自由端的拉力F=1/2T=1/2
×600N=300N.(3)当绳子被拉断时,绳子受到的拉力F′=350N,动滑轮对圆柱体的拉力T′=2F′=700N,此时的浮力为:F浮′=G-T′=1000N-700N=300NV排′=F′浮/ρ水g
=300N/1×103kg/m3×
10Nkg
=0.03m3,物体浸入水中的长度h′为:h′=V排′/S
=0.03m3/0.02m2
=1.5m.物体上升的高度为:L=H-h′=15m-1.5m=13.5m,圆柱体运动的时间:t=L/v
=13.5m
0.2m/s
=67.5s.17.用相同的滑轮和绳子分别组成如图所示的甲、乙两个滑轮组,把相同的重物匀速提升相同的高度.若不计绳重及摩擦,下列说法正确的是( ) A.绳子受的拉力F1和F2大小相等,滑轮组的机械效率相同 B.绳子受的拉力F1和F2大小不相等,滑轮组的机械效率不同 C.绳子自由端移动的距离不相等,拉力对滑轮组所做的功相等 D.绳子自由端移动的距离不相等,拉力对滑轮组所做的功不相等解答:不计绳重及摩擦,∵拉力F=(G物+G轮),n1=2,n2=3,∴绳子受的拉力:F1=(G物+G轮),F2=(G物+G轮),∴F1≠F2,∵动滑轮重相同,提升的物体重和高度相同,W额=G轮h,W有用=G物h,∴利用滑轮组做的有用功相同、额外功相同,总功相同,∵η=×100%,∴滑轮组的机械效率相同,故A、B错;∵绳子自由端移动的距离s=nh,n1=2,n2=3,提升物体的高度h相同,∴s1=2h,s2=3h,∴s1≠s2,拉力做的功:W1=F1s1=(G物+G轮)×2h=(G物+G轮)hW2=F2s2=(G物+G轮)×3h=(G物+G轮)h∴,W1=W2,故C正确、D错.故选C.18.用一个定滑轮和一个动滑轮组成的滑轮组把重150N的物体匀速提升1m,不计摩擦和绳重,滑轮组的机械效率为60%.则下列选项错误的是( ) A.拉力一定是125NB.有用功一定是150J C.总功一定是250JD.动滑轮重一定是100N解答:对左图滑轮组,承担物重的绳子股数n=3,对物体做的有用功:W有=Gh=150N×1m=150J,∵η=,∴W总===250J,∴W额=W总﹣W有=250J﹣150J=100J;∵不计绳重和摩擦,W额=G轮h,∴动滑轮重:G轮===100N,拉力F的大小:F=(G物+G轮)=(150N+100N)=N;对右图滑轮组,承担物重的绳子股数n=2,对物体做的有用功:W有=Gh=150N×1m=150J,∵η=,∴W总===250J,∴W额=W总﹣W有=250J﹣150J=100J;∵不计绳重和摩擦,W额=G轮h,∴动滑轮重:G轮===100N,拉力F的大小:F=(G物+G轮)=(150N+100N)=125N.由以上计算可知,对物体做的有用功都是150J,总功都是250J,动滑轮重都是100N,故B、C、D都正确;但拉力不同,故A错.故选A.19.用如图所示的机械拉着重500N的物体在水平地面上匀速运动,物体受到的摩擦力为120N,绳子末端的水平拉力为50N,则滑轮组的机械效率为
;若物体运动的速度为0.2m/s,则10s内拉力做的功是
J.解答:(1)物体在水平地面上匀速运动,需要克服的是物体与地面间的摩擦力.机械效率η=;故答案为:80%.(2)10s内拉力作用点移动的距离S拉=nS物=3×0.2m/s×10s=6m,拉力所做的功W总=FS拉=50N×6m=300J;故答案为:300.20.如图,小王站在高3m、长6m的斜面上,将重200N的木箱沿斜面匀速从底端拉上顶端,拉力大小恒为120N,所花时间是10s.求:(1)木箱A沿斜面方向的运动速度.(2)小王对木箱做功的功率.(3)斜面的机械效率.解答:(1)v===0.6m/s;(2)W总=Fs=120N×6m=720J,P===72W;(3)W有用=Gh=200N×3m=600J,η==≈83.3%.答:(1)木箱A沿斜面方向的运动速度为0.6m/s.(2)小王对木箱做功的功率72W.(3)斜面的机械效率83.3%.21.小明在探究利用杠杆做功的实践活动中,将重G为15N的重物挂在杠杆的中点,用手竖直提起棒的另一端,使物体缓慢匀速提升,如图所示.(1)不计杠杆自身重力和摩擦,求拉力F的大小?(2)如杠杆是一根重为5N质量均匀的硬棒,若在2s内将重物提升0.l0m,则重物上升的速度是多大?小明使用杠杆所做的有用功为多大?机械效率是多大?解答:(1)由杠杆原理可知:FL1=GL2,即==,F==7.5N.(2)v===0.05m/s,W有用=Gh=15N×0.1m=1.5J,W额外=G杆h=5N×0.1m=0.5J,W总=W有用+W额外=1.5J+0.5J=2J,η===75%.答:(1)不计杠杆自身重力和摩擦,拉力F是7.5N.(2)重物上升的速度是0.05m/s;小明使用杠杆所做的有用功为1.5J.机械效率是75%.下次课预习
l1
l2
F2
F1
l1
F2
l2
A
B
F甲
F乙
乙
O
·
甲
O
·
B
A
·
·
同课章节目录
