2016年北师大新版九年级数学上册同步测试:4.2 平行线分线段成比例(解析版)
文档属性
| 名称 | 2016年北师大新版九年级数学上册同步测试:4.2 平行线分线段成比例(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 155.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-19 00:00:00 | ||
图片预览




文档简介
2016年北师大新版九年级数学上册同步测试:4.2
平行线分线段成比例
一、选择题(共12小题)
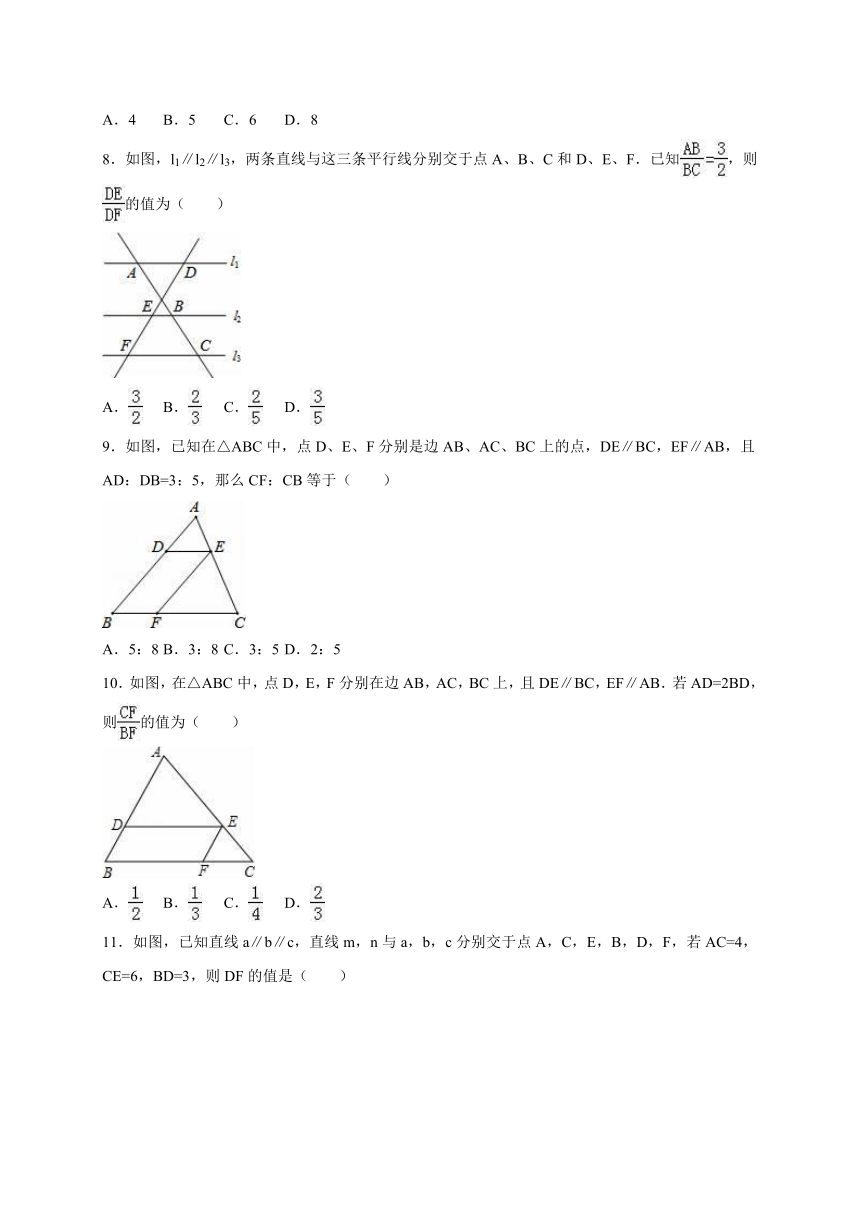
1.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,,则EC的长是( )
A.4.5
B.8
C.10.5
D.14
2.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若=,DE=4,则EF的长是( )
A.
B.
C.6
D.10
3.如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( )
A.2
B.4
C.6
D.8
4.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则的值为( )
A.
B.2
C.
D.
5.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为( )
A.
B.2
C.
D.
6.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
A.1
B.2
C.3
D.4
7.如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为( )
A.4
B.5
C.6
D.8
8.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知,则的值为( )
A.
B.
C.
D.
9.如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( )
A.5:8
B.3:8
C.3:5
D.2:5
10.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则的值为( )
A.
B.
C.
D.
11.如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=6,BD=3,则DF的值是( )
A.4
B.4.5
C.5
D.5.5
12.如图,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则的值是( )
A.
B.
C.
D.
二、填空题(共4小题)
13.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .
14.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,
=,DE=6,则EF= .
15.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC= cm.
16.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH的长为 .
2016年北师大新版九年级数学上册同步测试:4.2
平行线分线段成比例
参考答案与试题解析
一、选择题(共12小题)
1.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,,则EC的长是( )
A.4.5
B.8
C.10.5
D.14
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例定理列式进行计算即可得解.
【解答】解:∵DE∥BC,
∴=,
即=,
解得EC=8.
故选B.
【点评】本题考查了平行线分线段成比例定理,找准对应关系是解题的关键.
2.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若=,DE=4,则EF的长是( )
A.
B.
C.6
D.10
【考点】平行线分线段成比例.
【专题】压轴题.
【分析】根据平行线分线段成比例可得,代入计算即可解答.
【解答】解:∵l1∥l2∥l3,
∴,
即,
解得:EF=6.
故选:C.
【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.
3.如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( )
A.2
B.4
C.6
D.8
【考点】平行线分线段成比例;菱形的判定与性质;作图—基本作图.
【分析】根据已知得出MN是线段AD的垂直平分线,推出AE=DE,AF=DF,求出DE∥AC,DF∥AE,得出四边形AEDF是菱形,根据菱形的性质得出AE=DE=DF=AF,根据平行线分线段成比例定理得出=,代入求出即可.
【解答】解:∵根据作法可知:MN是线段AD的垂直平分线,
∴AE=DE,AF=DF,
∴∠EAD=∠EDA,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠EDA=∠CAD,
∴DE∥AC,
同理DF∥AE,
∴四边形AEDF是菱形,
∴AE=DE=DF=AF,
∵AF=4,
∴AE=DE=DF=AF=4,
∵DE∥AC,
∴=,
∵BD=6,AE=4,CD=3,
∴=,
∴BE=8,
故选D.
【点评】本题考查了平行线分线段成比例定理,菱形的性质和判定,线段垂直平分线性质,等腰三角形的性质的应用,能根据定理四边形AEDF是菱形是解此题的关键,注意:一组平行线截两条直线,所截得的对应线段成比例.
4.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则的值为( )
A.
B.2
C.
D.
【考点】平行线分线段成比例.
【分析】根据AH=2,HB=1求出AB的长,根据平行线分线段成比例定理得到=,计算得到答案.
【解答】解:∵AH=2,HB=1,
∴AB=3,
∵l1∥l2∥l3,
∴==,
故选:D.
【点评】本题考查平行线分线段成比例定理,掌握定理的内容、找准对应关系列出比例式是解题的关键.
5.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为( )
A.
B.2
C.
D.
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例可得,代入计算,可求得答案.
【解答】解:∵AG=2,GB=1,
∴AB=AG+BG=3,
∵直线l1∥l2∥l3,
∴=,
故选:D.
【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.
6.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
A.1
B.2
C.3
D.4
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例可得,代入计算即可解答.
【解答】解:∵DE∥BC,
∴,
即,
解得:EC=2,
故选:B.
【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.
7.如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为( )
A.4
B.5
C.6
D.8
【考点】平行线分线段成比例.
【分析】由AD∥BE∥CF可得=,代入可求得EF.
【解答】解:∵AD∥BE∥CF,
∴=,
∵AB=1,BC=3,DE=2,
∴=,
解得EF=6,
故选:C.
【点评】本题主要考查平行线分线段成比例的性质,掌握平行线分线段可得对应线段成比例是解题的关键.
8.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知,则的值为( )
A.
B.
C.
D.
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例定理得出=,根据已知即可求出答案.
【解答】解:∵l1∥l2∥l3,,
∴===,
故选:D.
【点评】本题考查了平行线分线段成比例定理的应用,能根据定理得出比例式是解此题的关键,注意:一组平行线截两条直线,所截得的对应线段成比例.
9.如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( )
A.5:8
B.3:8
C.3:5
D.2:5
【考点】平行线分线段成比例.
【分析】先由AD:DB=3:5,求得BD:AB的比,再由DE∥BC,根据平行线分线段成比例定理,可得CE:AC=BD:AB,然后由EF∥AB,根据平行线分线段成比例定理,可得CF:CB=CE:AC,则可求得答案.
【解答】解:∵AD:DB=3:5,
∴BD:AB=5:8,
∵DE∥BC,
∴CE:AC=BD:AB=5:8,
∵EF∥AB,
∴CF:CB=CE:AC=5:8.
故选A.
【点评】此题考查了平行线分线段成比例定理.此题比较简单,注意掌握比例线段的对应关系是解此题的关键.
10.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则的值为( )
A.
B.
C.
D.
【考点】平行线分线段成比例.
【专题】几何图形问题.
【分析】根据平行线分线段成比例定理得出===2,即可得出答案.
【解答】解:∵DE∥BC,EF∥AB,AD=2BD,
∴==2,
==2,
∴=,
故选:A.
【点评】本题考查了平行线分线段成比例定理的应用,注意:一组平行线截两条直线,所截得的对应线段成比例.
11.如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=6,BD=3,则DF的值是( )
A.4
B.4.5
C.5
D.5.5
【考点】平行线分线段成比例.
【分析】直接根据平行线分线段成比例定理即可得出结论.
【解答】解:∵直线a∥b∥c,AC=4,CE=6,BD=3,
∴=,即=,解得DF=4.5.
故选B.
【点评】本题考查的是平行线分线段成比例定理,熟知三条平行线截两条直线,所得的对应线段成比例是解答此题的关键.
12.如图,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则的值是( )
A.
B.
C.
D.
【考点】平行线分线段成比例;角平分线的性质;等腰直角三角形.
【专题】计算题.
【分析】作FG⊥AB于点G,由AE∥FG,得出=,求出Rt△BGF≌Rt△BCF,再由AB=BC求解.
【解答】解:作FG⊥AB于点G,
∵∠DAB=90°,
∴AE∥FG,
∴=,
∵AC⊥BC,
∴∠ACB=90°,
又∵BE是∠ABC的平分线,
∴FG=FC,
在Rt△BGF和Rt△BCF中,
∴Rt△BGF≌Rt△BCF(HL),
∴CB=GB,
∵AC=BC,
∴∠CBA=45°,
∴AB=BC,
∴====+1.
故选:C.
【点评】本题主要考查了平行线分线段成比例,全等三角形及角平分线的知识,解题的关键是找出线段之间的关系,CB=GB,AB=BC再利用比例式求解.
二、填空题(共4小题)
13.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例定理即可直接求解.
【解答】解:∵DE∥AC,
∴,
即,
解得:EC=.
故答案为:.
【点评】本题考查了平行线分线段成比例定理,理解定理内容是解题的关键.
14.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,
=,DE=6,则EF= 9 .
【考点】平行线分线段成比例.
【专题】计算题.
【分析】根据平行线分线段成比例定理得到=,即=,然后根据比例性质求EF.
【解答】解:∵AD∥BE∥CF,
∴=,即=,
∴EF=9.
故答案为9.
【点评】本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.
15.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC= 12 cm.
【考点】平行线分线段成比例.
【分析】过点A作AE⊥CE于点E,交BD于点D,根据平行线分线段成比例可得,代入计算即可解答.
【解答】解:如图,过点A作AE⊥CE于点E,交BD于点D,
∵练习本中的横格线都平行,且相邻两条横格线间的距离都相等,
∴,
即,
∴BC=12cm.
故答案为:12.
【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.
16.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH的长为 .
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例定理,由AB∥GH,得出=,由GH∥CD,得出=,将两个式子相加,即可求出GH的长.
【解答】解:∵AB∥GH,
∴=,即=①,
∵GH∥CD,
∴=,即=②,
①+②,得+=+==1,
∴+=1,
解得GH=.
故答案为.
【点评】本题考查了平行线分线段成比例定理,熟练运用等式的性质进行计算.本题难度适中.
平行线分线段成比例
一、选择题(共12小题)
1.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,,则EC的长是( )
A.4.5
B.8
C.10.5
D.14
2.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若=,DE=4,则EF的长是( )
A.
B.
C.6
D.10
3.如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( )
A.2
B.4
C.6
D.8
4.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则的值为( )
A.
B.2
C.
D.
5.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为( )
A.
B.2
C.
D.
6.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
A.1
B.2
C.3
D.4
7.如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为( )
A.4
B.5
C.6
D.8
8.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知,则的值为( )
A.
B.
C.
D.
9.如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( )
A.5:8
B.3:8
C.3:5
D.2:5
10.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则的值为( )
A.
B.
C.
D.
11.如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=6,BD=3,则DF的值是( )
A.4
B.4.5
C.5
D.5.5
12.如图,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则的值是( )
A.
B.
C.
D.
二、填空题(共4小题)
13.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .
14.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,
=,DE=6,则EF= .
15.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC= cm.
16.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH的长为 .
2016年北师大新版九年级数学上册同步测试:4.2
平行线分线段成比例
参考答案与试题解析
一、选择题(共12小题)
1.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,,则EC的长是( )
A.4.5
B.8
C.10.5
D.14
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例定理列式进行计算即可得解.
【解答】解:∵DE∥BC,
∴=,
即=,
解得EC=8.
故选B.
【点评】本题考查了平行线分线段成比例定理,找准对应关系是解题的关键.
2.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若=,DE=4,则EF的长是( )
A.
B.
C.6
D.10
【考点】平行线分线段成比例.
【专题】压轴题.
【分析】根据平行线分线段成比例可得,代入计算即可解答.
【解答】解:∵l1∥l2∥l3,
∴,
即,
解得:EF=6.
故选:C.
【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.
3.如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( )
A.2
B.4
C.6
D.8
【考点】平行线分线段成比例;菱形的判定与性质;作图—基本作图.
【分析】根据已知得出MN是线段AD的垂直平分线,推出AE=DE,AF=DF,求出DE∥AC,DF∥AE,得出四边形AEDF是菱形,根据菱形的性质得出AE=DE=DF=AF,根据平行线分线段成比例定理得出=,代入求出即可.
【解答】解:∵根据作法可知:MN是线段AD的垂直平分线,
∴AE=DE,AF=DF,
∴∠EAD=∠EDA,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠EDA=∠CAD,
∴DE∥AC,
同理DF∥AE,
∴四边形AEDF是菱形,
∴AE=DE=DF=AF,
∵AF=4,
∴AE=DE=DF=AF=4,
∵DE∥AC,
∴=,
∵BD=6,AE=4,CD=3,
∴=,
∴BE=8,
故选D.
【点评】本题考查了平行线分线段成比例定理,菱形的性质和判定,线段垂直平分线性质,等腰三角形的性质的应用,能根据定理四边形AEDF是菱形是解此题的关键,注意:一组平行线截两条直线,所截得的对应线段成比例.
4.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则的值为( )
A.
B.2
C.
D.
【考点】平行线分线段成比例.
【分析】根据AH=2,HB=1求出AB的长,根据平行线分线段成比例定理得到=,计算得到答案.
【解答】解:∵AH=2,HB=1,
∴AB=3,
∵l1∥l2∥l3,
∴==,
故选:D.
【点评】本题考查平行线分线段成比例定理,掌握定理的内容、找准对应关系列出比例式是解题的关键.
5.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为( )
A.
B.2
C.
D.
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例可得,代入计算,可求得答案.
【解答】解:∵AG=2,GB=1,
∴AB=AG+BG=3,
∵直线l1∥l2∥l3,
∴=,
故选:D.
【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.
6.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
A.1
B.2
C.3
D.4
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例可得,代入计算即可解答.
【解答】解:∵DE∥BC,
∴,
即,
解得:EC=2,
故选:B.
【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.
7.如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为( )
A.4
B.5
C.6
D.8
【考点】平行线分线段成比例.
【分析】由AD∥BE∥CF可得=,代入可求得EF.
【解答】解:∵AD∥BE∥CF,
∴=,
∵AB=1,BC=3,DE=2,
∴=,
解得EF=6,
故选:C.
【点评】本题主要考查平行线分线段成比例的性质,掌握平行线分线段可得对应线段成比例是解题的关键.
8.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知,则的值为( )
A.
B.
C.
D.
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例定理得出=,根据已知即可求出答案.
【解答】解:∵l1∥l2∥l3,,
∴===,
故选:D.
【点评】本题考查了平行线分线段成比例定理的应用,能根据定理得出比例式是解此题的关键,注意:一组平行线截两条直线,所截得的对应线段成比例.
9.如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( )
A.5:8
B.3:8
C.3:5
D.2:5
【考点】平行线分线段成比例.
【分析】先由AD:DB=3:5,求得BD:AB的比,再由DE∥BC,根据平行线分线段成比例定理,可得CE:AC=BD:AB,然后由EF∥AB,根据平行线分线段成比例定理,可得CF:CB=CE:AC,则可求得答案.
【解答】解:∵AD:DB=3:5,
∴BD:AB=5:8,
∵DE∥BC,
∴CE:AC=BD:AB=5:8,
∵EF∥AB,
∴CF:CB=CE:AC=5:8.
故选A.
【点评】此题考查了平行线分线段成比例定理.此题比较简单,注意掌握比例线段的对应关系是解此题的关键.
10.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则的值为( )
A.
B.
C.
D.
【考点】平行线分线段成比例.
【专题】几何图形问题.
【分析】根据平行线分线段成比例定理得出===2,即可得出答案.
【解答】解:∵DE∥BC,EF∥AB,AD=2BD,
∴==2,
==2,
∴=,
故选:A.
【点评】本题考查了平行线分线段成比例定理的应用,注意:一组平行线截两条直线,所截得的对应线段成比例.
11.如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=6,BD=3,则DF的值是( )
A.4
B.4.5
C.5
D.5.5
【考点】平行线分线段成比例.
【分析】直接根据平行线分线段成比例定理即可得出结论.
【解答】解:∵直线a∥b∥c,AC=4,CE=6,BD=3,
∴=,即=,解得DF=4.5.
故选B.
【点评】本题考查的是平行线分线段成比例定理,熟知三条平行线截两条直线,所得的对应线段成比例是解答此题的关键.
12.如图,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则的值是( )
A.
B.
C.
D.
【考点】平行线分线段成比例;角平分线的性质;等腰直角三角形.
【专题】计算题.
【分析】作FG⊥AB于点G,由AE∥FG,得出=,求出Rt△BGF≌Rt△BCF,再由AB=BC求解.
【解答】解:作FG⊥AB于点G,
∵∠DAB=90°,
∴AE∥FG,
∴=,
∵AC⊥BC,
∴∠ACB=90°,
又∵BE是∠ABC的平分线,
∴FG=FC,
在Rt△BGF和Rt△BCF中,
∴Rt△BGF≌Rt△BCF(HL),
∴CB=GB,
∵AC=BC,
∴∠CBA=45°,
∴AB=BC,
∴====+1.
故选:C.
【点评】本题主要考查了平行线分线段成比例,全等三角形及角平分线的知识,解题的关键是找出线段之间的关系,CB=GB,AB=BC再利用比例式求解.
二、填空题(共4小题)
13.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例定理即可直接求解.
【解答】解:∵DE∥AC,
∴,
即,
解得:EC=.
故答案为:.
【点评】本题考查了平行线分线段成比例定理,理解定理内容是解题的关键.
14.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,
=,DE=6,则EF= 9 .
【考点】平行线分线段成比例.
【专题】计算题.
【分析】根据平行线分线段成比例定理得到=,即=,然后根据比例性质求EF.
【解答】解:∵AD∥BE∥CF,
∴=,即=,
∴EF=9.
故答案为9.
【点评】本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.
15.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC= 12 cm.
【考点】平行线分线段成比例.
【分析】过点A作AE⊥CE于点E,交BD于点D,根据平行线分线段成比例可得,代入计算即可解答.
【解答】解:如图,过点A作AE⊥CE于点E,交BD于点D,
∵练习本中的横格线都平行,且相邻两条横格线间的距离都相等,
∴,
即,
∴BC=12cm.
故答案为:12.
【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.
16.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH的长为 .
【考点】平行线分线段成比例.
【分析】根据平行线分线段成比例定理,由AB∥GH,得出=,由GH∥CD,得出=,将两个式子相加,即可求出GH的长.
【解答】解:∵AB∥GH,
∴=,即=①,
∵GH∥CD,
∴=,即=②,
①+②,得+=+==1,
∴+=1,
解得GH=.
故答案为.
【点评】本题考查了平行线分线段成比例定理,熟练运用等式的性质进行计算.本题难度适中.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
