24.4解直角三角形 复习教案
图片预览

文档简介
解直角三角形
1、一个直角三角形中,若已知五个元素中的两个元素(其中必须有一个元素是边),则这样的直角三角形可解。
五个元素:两个锐角、三条边
Rt△ABC中:∠A,∠B,a,b,c即为直角三角形的五个元素.
三边之间的关系:
两锐角之间的关系
∠A+∠B=90°
边角之间的关系:
2、解直角三角形时,要注意适当选用恰含一个未知数的关系式。
在Rt△ABC中,∠C=90°
已知∠A、c,则;
已知一锐角、斜边,求对边,用锐角的正弦;求邻边,用锐角的余弦。
已知∠A、b,则;
已知一锐角,邻边,求对边,用锐角的正切;求斜边,用锐角的余弦。
已知∠A,a,则;
已知一锐角、对边,
求邻边,用锐角的余切;求斜边,用锐角的正弦。
已知a、b,则
已知a、c,则
3、选用关系式归纳为口诀
已知斜边求直边,正弦余弦很方便;
已知直边求直边,正切余切理当然;
已知两边求一边,勾股定理最方便;
已知两边求一角,函数关系要选好;
已知锐角求锐角,互余关系要记好;
已知直边求斜边,用除还需正余弦;
计算方法要选择,能用乘法不用除。
4、典型例题:
在Rt△ABC中,∠C=90°,a=32,b=,解三角形。
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
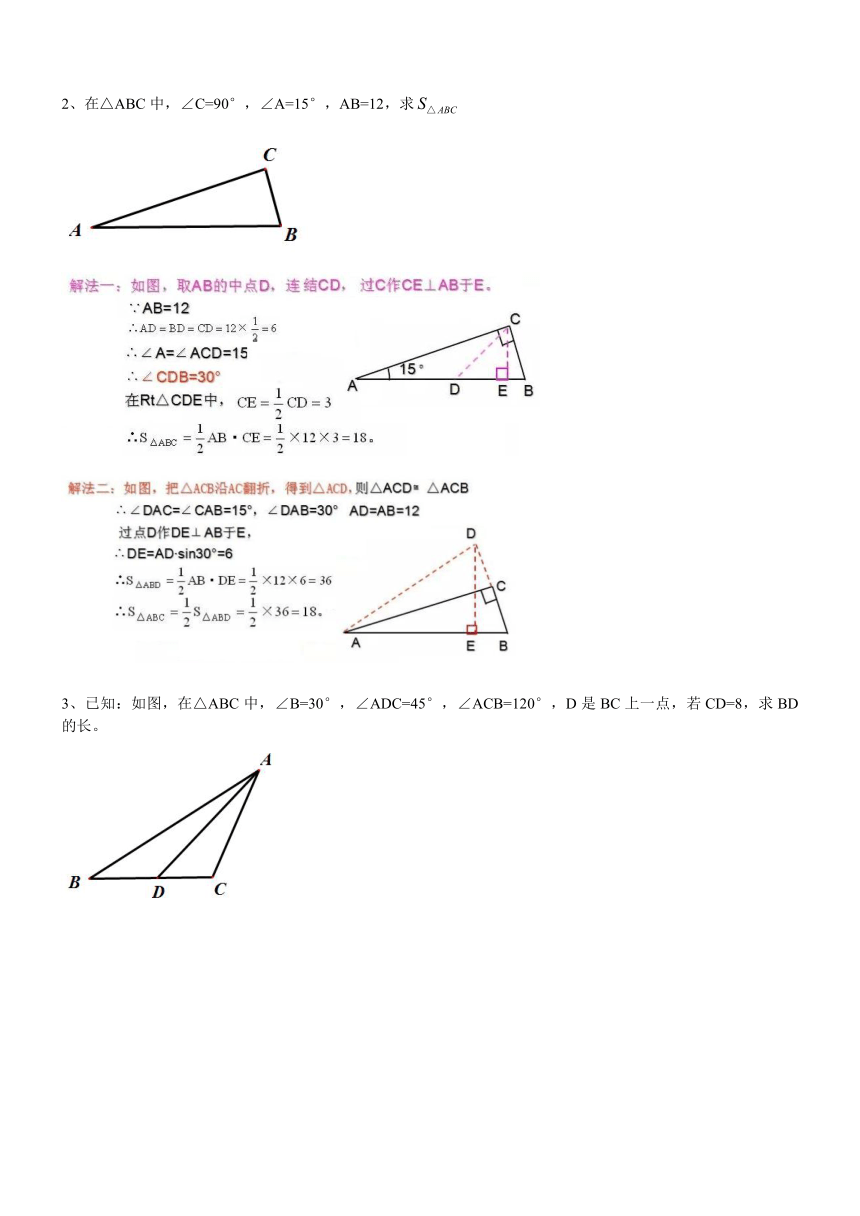
在△ABC中,∠C=90°,∠A=15°,AB=12,求
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
3、已知:如图,在△ABC中,∠B=30°,∠ADC=45°,∠ACB=120°,D是BC上一点,若CD=8,求BD的长。
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
解直角三角形的应用
基本概念:
仰角:视线与水平线的夹角
俯角:视线与水平线的夹角
坡度:坡面的垂直高度和水平宽度的比叫坡度(或叫坡比)
坡度角:坡面与水平面的夹角
例1
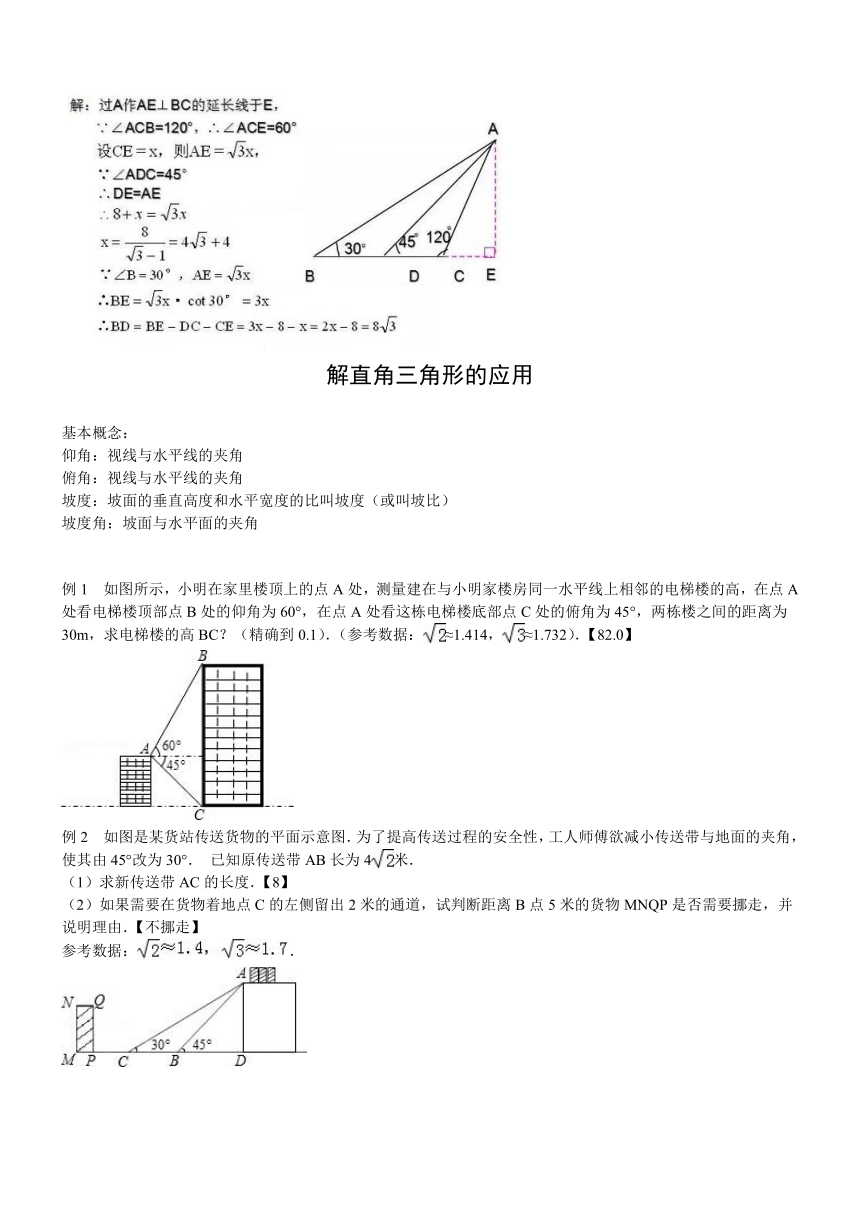
如图所示,小明在家里楼顶上的点A处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A处看电梯楼顶部点B处的仰角为60°,在点A处看这栋电梯楼底部点C处的俯角为45°,两栋楼之间的距离为30m,求电梯楼的高BC?(精确到0.1).(参考数据:≈1.414,≈1.732).【82.0】
( http: / / www.21cnjy.com )
例2
如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.
已知原传送带AB长为4米.
(1)求新传送带AC的长度.【8】
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.【不挪走】
参考数据:.
( http: / / www.21cnjy.com )
例3
如图,一架飞机在空中P处探测到某
( http: / / www.21cnjy.com )高山山顶D处的俯角为60°,此后飞机以300米/秒的速度沿平行于地面AB的方向匀速飞行,飞行10秒到山顶D的正上方C处,此时测得飞机距地平面的垂直高度为12千米,求这座山的高(精确到0.1千米)【6.8】
( http: / / www.21cnjy.com )
1、2009年首届中国国际航空体育节在莱芜雪野举办,期间在市政府广场进行了热气球飞行表演.如图,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,)【15.6】
( http: / / www.21cnjy.com )
2、图1为已建设封项的16层楼房和其塔吊图
( http: / / www.21cnjy.com ),图2为其示意图,吊臂AB与地面EH平行,测得A点到楼顶D点的距离为5m,每层楼高3.5m,AE、BF、CH都垂直于地面,EF=16m,求塔吊的高CH的长?【69】
( http: / / www.21cnjy.com )
3、在一个阳光明媚、清风徐来的周末,小明和
( http: / / www.21cnjy.com )小强一起到郊外放风筝﹒他们把风筝放飞后,将两个风筝的引线一端都固定在地面上的C处(如图).现已知风筝A的引线(线段AC)长20m,风筝B的引线(线段BC)长24m,在C处测得风筝A的仰角为60°,风筝B的仰角为45°.
(1)试通过计算,比较风筝A与风筝B谁离地面更高?【A更高】
(2)求风筝A与风筝B的水
( http: / / www.21cnjy.com )平距离.(精确到0.01m;参考数据:sin45°≈0.707,cos45°≈0.707,tan45°=1,sin60°≈0.866,cos60°=0.5,tan60°≈1.732)【6.97】
( http: / / www.21cnjy.com )
4、永乐桥摩天轮是天津市的标志性景观之一某校数学兴趣小组要测量摩天轮的高度如图,他们在C处测得摩天轮的最高点A的仰角为45°,再往摩天轮的方向前进50m至D处,测得最高点A的仰角为60°.求该兴趣小组测得的摩天轮的高度AB.(,结果保留整数)【118】
( http: / / www.21cnjy.com )
参考数据
cos20°≈0.94
sin20°≈0.34
sin18°≈0.31
cos18°≈0.95
5、施工队准备在一段斜坡上铺上台阶方便通行.现测得斜坡上铅垂的两棵树间水平距离
AB=4米,斜面距离BC=4.25米,斜坡总长DE=85米.
(1)求坡角∠D的度数(结果精确到1°);【20°】
(2)若这段斜坡用厚度为17cm的长方体台阶来铺,需要铺几级台阶?【170】
( http: / / www.21cnjy.com )
6、如图,大海中有A和B两个岛屿,为测
( http: / / www.21cnjy.com )量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
(1)判断AB,AE的数量关系,并说明理由;【相等】
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).【3.6】
(参考数据:≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
( http: / / www.21cnjy.com )
7、在东西方向的海岸线L上有一长为1km的码头MN(如图),在码头西端M
的正西19.5km
处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于
A
的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距km的C处.
(1)求该轮船航行的速度(保留精确结果);【】
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由;【可以】
(3)根据(2)的探究过程,请求出要使从B出发的轮船靠岸,那么轮船的航线y=kx+b的k的取值范围?(直接写出答案)【】
( http: / / www.21cnjy.com )
8、如图,某天然气公司的主输气管道
( http: / / www.21cnjy.com )从A市的东偏北30°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市东偏北60°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西60°方向,请你在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,并求AN的长?【150】
( http: / / www.21cnjy.com )
9、小明想知道湖中两个小亭A、B之
( http: / / www.21cnjy.com )间的距离,他在与小亭A、B位于同一水平面且东西走向的湖边小道l上某一观测点M处,测得亭A在点M的北偏东30°,亭B在点M的北偏东60°,当小明由点M沿小道l向东走60米时,到达点N处,此时测得亭A恰好位于点N的正北方向,继续向东走30米时到达点Q处,此时亭B恰好位于点Q的正北方向,根据以上测量数据,请你帮助小明计算湖中两个小亭A、B之间的距离.【60】
( http: / / www.21cnjy.com )
1、一个直角三角形中,若已知五个元素中的两个元素(其中必须有一个元素是边),则这样的直角三角形可解。
五个元素:两个锐角、三条边
Rt△ABC中:∠A,∠B,a,b,c即为直角三角形的五个元素.
三边之间的关系:
两锐角之间的关系
∠A+∠B=90°
边角之间的关系:
2、解直角三角形时,要注意适当选用恰含一个未知数的关系式。
在Rt△ABC中,∠C=90°
已知∠A、c,则;
已知一锐角、斜边,求对边,用锐角的正弦;求邻边,用锐角的余弦。
已知∠A、b,则;
已知一锐角,邻边,求对边,用锐角的正切;求斜边,用锐角的余弦。
已知∠A,a,则;
已知一锐角、对边,
求邻边,用锐角的余切;求斜边,用锐角的正弦。
已知a、b,则
已知a、c,则
3、选用关系式归纳为口诀
已知斜边求直边,正弦余弦很方便;
已知直边求直边,正切余切理当然;
已知两边求一边,勾股定理最方便;
已知两边求一角,函数关系要选好;
已知锐角求锐角,互余关系要记好;
已知直边求斜边,用除还需正余弦;
计算方法要选择,能用乘法不用除。
4、典型例题:
在Rt△ABC中,∠C=90°,a=32,b=,解三角形。
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
在△ABC中,∠C=90°,∠A=15°,AB=12,求
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
3、已知:如图,在△ABC中,∠B=30°,∠ADC=45°,∠ACB=120°,D是BC上一点,若CD=8,求BD的长。
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
解直角三角形的应用
基本概念:
仰角:视线与水平线的夹角
俯角:视线与水平线的夹角
坡度:坡面的垂直高度和水平宽度的比叫坡度(或叫坡比)
坡度角:坡面与水平面的夹角
例1
如图所示,小明在家里楼顶上的点A处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A处看电梯楼顶部点B处的仰角为60°,在点A处看这栋电梯楼底部点C处的俯角为45°,两栋楼之间的距离为30m,求电梯楼的高BC?(精确到0.1).(参考数据:≈1.414,≈1.732).【82.0】
( http: / / www.21cnjy.com )
例2
如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.
已知原传送带AB长为4米.
(1)求新传送带AC的长度.【8】
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.【不挪走】
参考数据:.
( http: / / www.21cnjy.com )
例3
如图,一架飞机在空中P处探测到某
( http: / / www.21cnjy.com )高山山顶D处的俯角为60°,此后飞机以300米/秒的速度沿平行于地面AB的方向匀速飞行,飞行10秒到山顶D的正上方C处,此时测得飞机距地平面的垂直高度为12千米,求这座山的高(精确到0.1千米)【6.8】
( http: / / www.21cnjy.com )
1、2009年首届中国国际航空体育节在莱芜雪野举办,期间在市政府广场进行了热气球飞行表演.如图,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,)【15.6】
( http: / / www.21cnjy.com )
2、图1为已建设封项的16层楼房和其塔吊图
( http: / / www.21cnjy.com ),图2为其示意图,吊臂AB与地面EH平行,测得A点到楼顶D点的距离为5m,每层楼高3.5m,AE、BF、CH都垂直于地面,EF=16m,求塔吊的高CH的长?【69】
( http: / / www.21cnjy.com )
3、在一个阳光明媚、清风徐来的周末,小明和
( http: / / www.21cnjy.com )小强一起到郊外放风筝﹒他们把风筝放飞后,将两个风筝的引线一端都固定在地面上的C处(如图).现已知风筝A的引线(线段AC)长20m,风筝B的引线(线段BC)长24m,在C处测得风筝A的仰角为60°,风筝B的仰角为45°.
(1)试通过计算,比较风筝A与风筝B谁离地面更高?【A更高】
(2)求风筝A与风筝B的水
( http: / / www.21cnjy.com )平距离.(精确到0.01m;参考数据:sin45°≈0.707,cos45°≈0.707,tan45°=1,sin60°≈0.866,cos60°=0.5,tan60°≈1.732)【6.97】
( http: / / www.21cnjy.com )
4、永乐桥摩天轮是天津市的标志性景观之一某校数学兴趣小组要测量摩天轮的高度如图,他们在C处测得摩天轮的最高点A的仰角为45°,再往摩天轮的方向前进50m至D处,测得最高点A的仰角为60°.求该兴趣小组测得的摩天轮的高度AB.(,结果保留整数)【118】
( http: / / www.21cnjy.com )
参考数据
cos20°≈0.94
sin20°≈0.34
sin18°≈0.31
cos18°≈0.95
5、施工队准备在一段斜坡上铺上台阶方便通行.现测得斜坡上铅垂的两棵树间水平距离
AB=4米,斜面距离BC=4.25米,斜坡总长DE=85米.
(1)求坡角∠D的度数(结果精确到1°);【20°】
(2)若这段斜坡用厚度为17cm的长方体台阶来铺,需要铺几级台阶?【170】
( http: / / www.21cnjy.com )
6、如图,大海中有A和B两个岛屿,为测
( http: / / www.21cnjy.com )量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
(1)判断AB,AE的数量关系,并说明理由;【相等】
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).【3.6】
(参考数据:≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
( http: / / www.21cnjy.com )
7、在东西方向的海岸线L上有一长为1km的码头MN(如图),在码头西端M
的正西19.5km
处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于
A
的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距km的C处.
(1)求该轮船航行的速度(保留精确结果);【】
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由;【可以】
(3)根据(2)的探究过程,请求出要使从B出发的轮船靠岸,那么轮船的航线y=kx+b的k的取值范围?(直接写出答案)【】
( http: / / www.21cnjy.com )
8、如图,某天然气公司的主输气管道
( http: / / www.21cnjy.com )从A市的东偏北30°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市东偏北60°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西60°方向,请你在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,并求AN的长?【150】
( http: / / www.21cnjy.com )
9、小明想知道湖中两个小亭A、B之
( http: / / www.21cnjy.com )间的距离,他在与小亭A、B位于同一水平面且东西走向的湖边小道l上某一观测点M处,测得亭A在点M的北偏东30°,亭B在点M的北偏东60°,当小明由点M沿小道l向东走60米时,到达点N处,此时测得亭A恰好位于点N的正北方向,继续向东走30米时到达点Q处,此时亭B恰好位于点Q的正北方向,根据以上测量数据,请你帮助小明计算湖中两个小亭A、B之间的距离.【60】
( http: / / www.21cnjy.com )
