空间直角坐标系
图片预览




文档简介
课件29张PPT。空间直角坐标系
蚌埠九中 罗培涛回顾1 在初中,我们学过数轴,那么什么是
数轴?决定数轴的因素有哪些?数轴上的
点怎么表示?数轴是规定了原点、正方向和单位长度的直线。x数轴上的点可用与这个点对应的实数x来表示。一维坐标 在初中,我们学过平面直角坐标系,那
么如何建立平面直角坐标系?决定的因素有
哪些?平面直角坐标系上的点怎么表示? 平面直角坐标系是由两条
原点重合、互相垂直的数轴
组成的。回顾2 平面直角坐标系上的点用
它对应的横、纵坐标,即一
对有序实数对(x,y)表示。二维坐标思考1: 在空间,我们是否可以建立一个坐标系,
使空间中的任意一点都可用对应的有序实数
组表示出来呢?猜想: 空间中的点可用有序实数
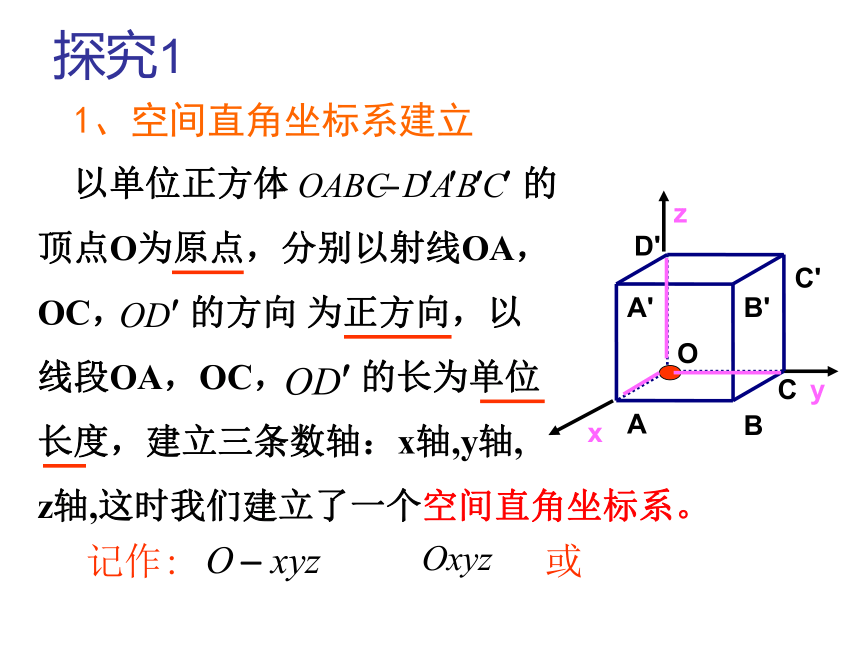
组(x,y,z)表示。 探究11、空间直角坐标系建立 以单位正方体 的
顶点O为原点,分别以射线OA,
OC, 的方向 为正方向,以
线段OA,OC, 的长为单位
长度,建立三条数轴:x轴,y轴,
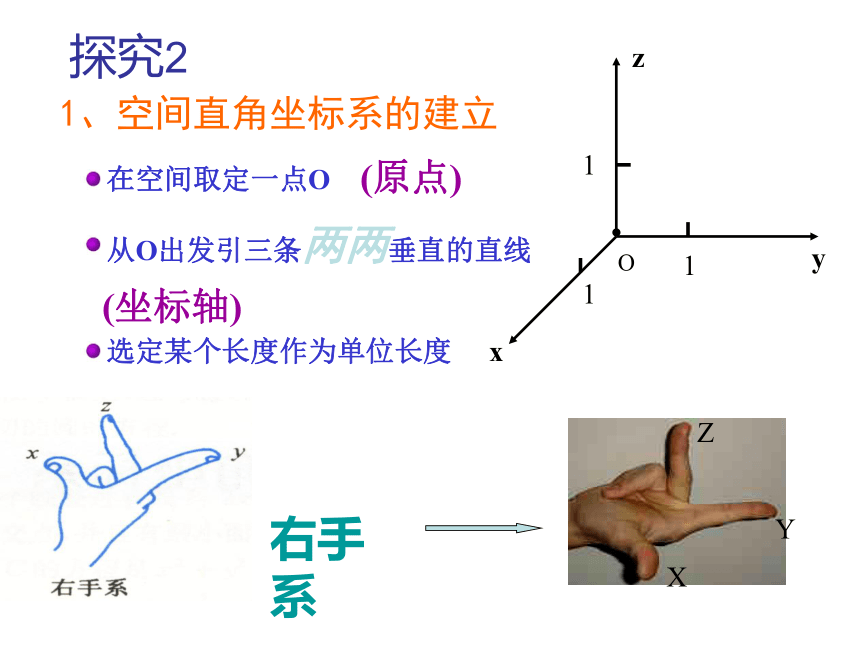
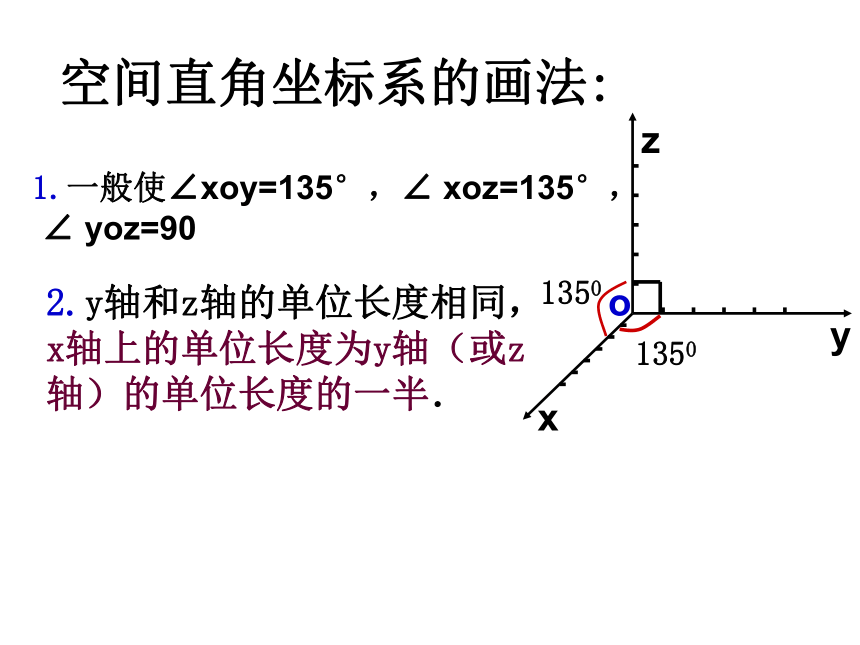
z轴,这时我们建立了一个空间直角坐标系。记作: 或1、空间直角坐标系的建立在空间取定一点O从O出发引三条两两垂直的直线选定某个长度作为单位长度(原点)(坐标轴)探究2空间直角坐标系的画法:o1.一般使∠xoy=135°,∠ xoz=135°,
∠ yoz=90 2.y轴和z轴的单位长度相同,x轴上的单位长度为y轴(或z轴)的单位长度的一半.通过每两个坐标轴的
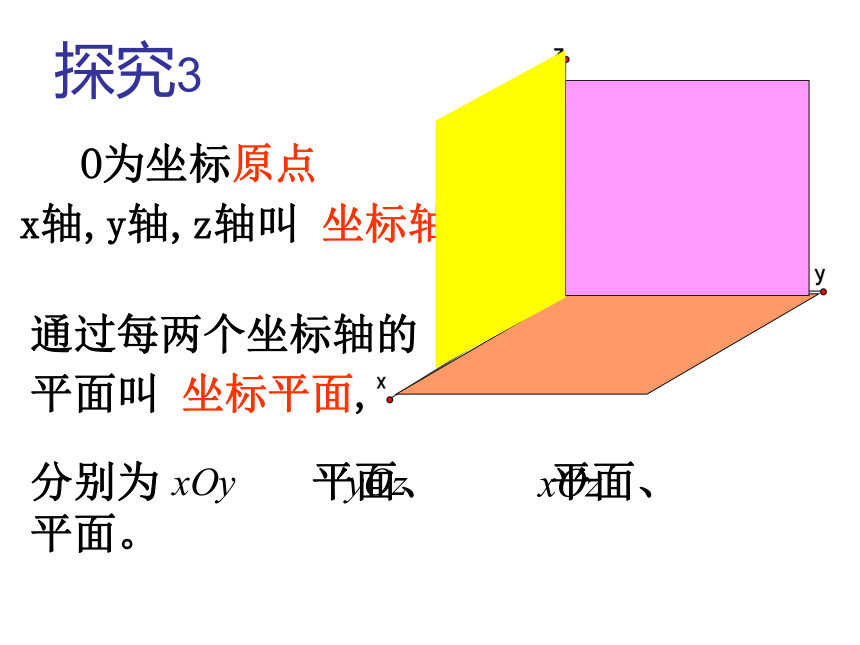
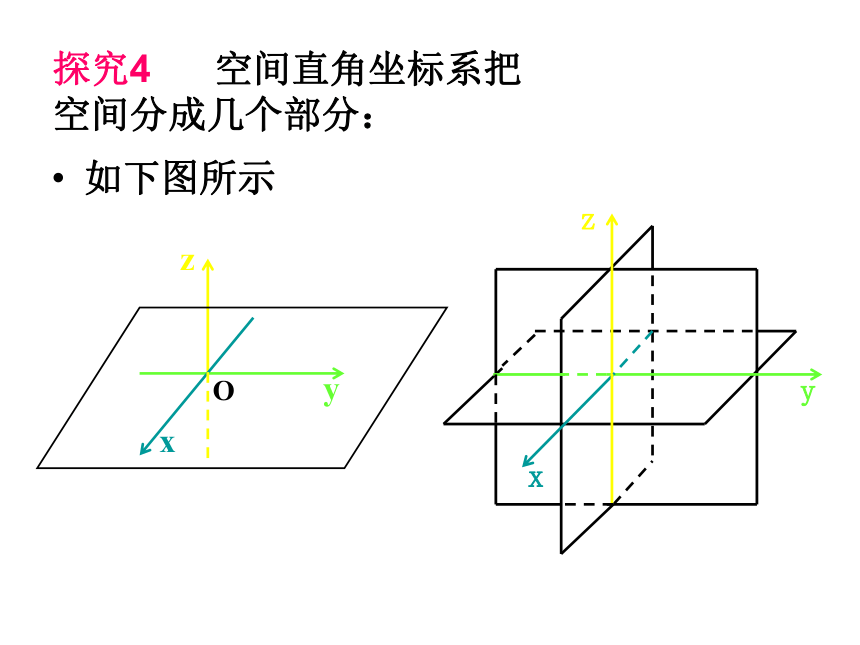
平面叫 坐标平面,探究3O为坐标原点x轴,y轴,z轴叫 坐标轴分别为 平面、 平面、 平面。如下图所示探究4 空间直角坐标系把空间分成几个部分:xoz面xoy面yoz面空间直角坐标系共有八个卦限2、空间直角坐标系的划分思考2: 空间直角坐标系中任意一点的位置如何表示?
?P1P2P3yxz??3、空间中的点的坐标对于空间任意一点P,要求它的坐标 方法一:过P点分别做三个平面分别垂直于x,y,z轴,平面与三个坐标轴的交点分别为P1、P2、P3,在其相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点P的空间直角坐标,简称为坐标,记作P(x,y,z),三个数值
叫做 P点的横坐标、纵坐标、竖坐标。??P0xyz P点坐标为
(x,y,z)P13、空间中点的坐标 方法二:过P点作xOy面的垂线,垂足为 点。点 在坐标系xOy中的坐标x、y依次是P点的横坐标、纵坐标。再过P点作z轴的垂线,垂足 在z轴上的坐标z就是P点的竖坐标。MN 3、在建立了空间直角坐标系后,空间中任何一点P就与有序实数组(x,y,z)建立了一一对应关系.注意: 2、有序实数组(x,y,z)就叫做P的空间直角坐标,简称为坐标,记作P(x,y,z)。
1、在第一卦限中,点的横、纵、竖坐标即为
该点分别到 平面、 平面、 平面的距离。小提示:坐标轴上的点至少有两个坐标等于0;坐标面上的点至少有一个坐标等于0。(0,0,0)(x,0,0)(0,y,0)(0,0,z)(x,y,0)(0,y,z)(x,0,z)4、特殊位置的点的坐标xoy平面上的点竖坐标为0yoz平面上的点横坐标为0xoz平面上的点纵坐标为0x轴上的点纵坐标和竖坐标都为0z轴上的点横坐标和纵坐标都为0y轴上的点横坐标和竖坐标都为0一、坐标平面内的点二、坐标轴上的点规律总结:例1:
D’ (0,0,2)C (0,4,0)A’ (3,0,2)B’ (3,4,2) 结晶体的基本单位称为晶胞,如图是食盐晶胞示意图(可看成是八个棱长为1/2的小正方体堆积成的正方体),其中红色点代表钠原子,黑点代表氯原子,如图:建立空间直角坐标系 后,
试写出全部钠原子
所在位置的坐标。例2:练习:???ABC?DEF??在空间直角坐标系中描出下列各点,并说明这些点的位置
A(0,1,1) B(0,0,2) C(0,2,0)
D(1,0,3) E(2,2,0) F(1,0,0)(+,+,+)5、点P在各卦限中x、y、z坐标的符号(-,+,+)(-,-,+)(+,-,+)(+,+,-)(-,+,-)(-,-,-)(+,-,-)卦限图卦限图?A1(1,4,0)?A(1,4,1)?(2,-2,0)
B1? B
(2,-2,-1)?(-1,-3,0)
C1?(-1,-3,3)
C练习:在空间直角坐标系中作出下列各点
(1)、A(1,4,1);
(2)、B(2,-2,-1);
(3)、C(-1,-3,3);思考3:设点M的坐标为(x,y,z)那么点M关于x轴、y轴、z轴及原点对称的点的坐标分别是什么?M(x,y,z)N(x,-y,-z)练习:规律:关于谁对称谁不变1.关于原点对称的为 (-x,-y,-z)空间直角坐标系中任一点p(x,y,z)2.关于x轴对称的为 (x,-y,-z)3.关于y轴对称的为 (-x, y,-z)4.关于z轴对称的为 (-x,-y, z)例:(1,2,3)(-1,-2,-3)(-1,-2,3)(-1,2,-3)(1,-2,-3)5.关于xoy平面对称的点为(x,y,-z)(1,2,-3)6.关于xoz平面对称的点为(x,-y,z)(1,-2,3)7.关于yoz平面对称的点为(-x,y,z)(-1,2,3)思考4:
若点A(x1,y1,z1),B(x2,y2,z2),则线段AB的中点M的坐标如何?随堂练习求下列各点的坐标1.2.3.4.思考5:点P1(x1,y1,z1)与P2(x2,y2,z2)之间的距离是
它对任意两点P1、P2都成立吗? 1. 在空间中,已知点A(1, 0, -1),B (4, 3, -1),求A、B两点之间的距离.练习: 2. 已知两点 A(-4, 1, 7)和B(3, 5, 2),点P在z轴上,若|PA|=|PB|,求点P的坐标. 3. 已知A(3,-2,-1),B(-1,-3,2),C(-5,-4,5),试判断A,B,C三点是否共线 4. 已知□ABCD的顶点A(4,1,3),B(2,-5,1),C(3,7,-5),求顶点D的坐标思考6:在空间直角坐标系中,方程 x2+y2+z2=r2(r>0为常数)表示什么图形是什么? 若r为常数,那么x2+y2+z2=r2表示以(0,0,0)为球心的球面谢谢观赏
数轴?决定数轴的因素有哪些?数轴上的
点怎么表示?数轴是规定了原点、正方向和单位长度的直线。x数轴上的点可用与这个点对应的实数x来表示。一维坐标 在初中,我们学过平面直角坐标系,那
么如何建立平面直角坐标系?决定的因素有
哪些?平面直角坐标系上的点怎么表示? 平面直角坐标系是由两条
原点重合、互相垂直的数轴
组成的。回顾2 平面直角坐标系上的点用
它对应的横、纵坐标,即一
对有序实数对(x,y)表示。二维坐标思考1: 在空间,我们是否可以建立一个坐标系,
使空间中的任意一点都可用对应的有序实数
组表示出来呢?猜想: 空间中的点可用有序实数
组(x,y,z)表示。 探究11、空间直角坐标系建立 以单位正方体 的
顶点O为原点,分别以射线OA,
OC, 的方向 为正方向,以
线段OA,OC, 的长为单位
长度,建立三条数轴:x轴,y轴,
z轴,这时我们建立了一个空间直角坐标系。记作: 或1、空间直角坐标系的建立在空间取定一点O从O出发引三条两两垂直的直线选定某个长度作为单位长度(原点)(坐标轴)探究2空间直角坐标系的画法:o1.一般使∠xoy=135°,∠ xoz=135°,
∠ yoz=90 2.y轴和z轴的单位长度相同,x轴上的单位长度为y轴(或z轴)的单位长度的一半.通过每两个坐标轴的
平面叫 坐标平面,探究3O为坐标原点x轴,y轴,z轴叫 坐标轴分别为 平面、 平面、 平面。如下图所示探究4 空间直角坐标系把空间分成几个部分:xoz面xoy面yoz面空间直角坐标系共有八个卦限2、空间直角坐标系的划分思考2: 空间直角坐标系中任意一点的位置如何表示?
?P1P2P3yxz??3、空间中的点的坐标对于空间任意一点P,要求它的坐标 方法一:过P点分别做三个平面分别垂直于x,y,z轴,平面与三个坐标轴的交点分别为P1、P2、P3,在其相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点P的空间直角坐标,简称为坐标,记作P(x,y,z),三个数值
叫做 P点的横坐标、纵坐标、竖坐标。??P0xyz P点坐标为
(x,y,z)P13、空间中点的坐标 方法二:过P点作xOy面的垂线,垂足为 点。点 在坐标系xOy中的坐标x、y依次是P点的横坐标、纵坐标。再过P点作z轴的垂线,垂足 在z轴上的坐标z就是P点的竖坐标。MN 3、在建立了空间直角坐标系后,空间中任何一点P就与有序实数组(x,y,z)建立了一一对应关系.注意: 2、有序实数组(x,y,z)就叫做P的空间直角坐标,简称为坐标,记作P(x,y,z)。
1、在第一卦限中,点的横、纵、竖坐标即为
该点分别到 平面、 平面、 平面的距离。小提示:坐标轴上的点至少有两个坐标等于0;坐标面上的点至少有一个坐标等于0。(0,0,0)(x,0,0)(0,y,0)(0,0,z)(x,y,0)(0,y,z)(x,0,z)4、特殊位置的点的坐标xoy平面上的点竖坐标为0yoz平面上的点横坐标为0xoz平面上的点纵坐标为0x轴上的点纵坐标和竖坐标都为0z轴上的点横坐标和纵坐标都为0y轴上的点横坐标和竖坐标都为0一、坐标平面内的点二、坐标轴上的点规律总结:例1:
D’ (0,0,2)C (0,4,0)A’ (3,0,2)B’ (3,4,2) 结晶体的基本单位称为晶胞,如图是食盐晶胞示意图(可看成是八个棱长为1/2的小正方体堆积成的正方体),其中红色点代表钠原子,黑点代表氯原子,如图:建立空间直角坐标系 后,
试写出全部钠原子
所在位置的坐标。例2:练习:???ABC?DEF??在空间直角坐标系中描出下列各点,并说明这些点的位置
A(0,1,1) B(0,0,2) C(0,2,0)
D(1,0,3) E(2,2,0) F(1,0,0)(+,+,+)5、点P在各卦限中x、y、z坐标的符号(-,+,+)(-,-,+)(+,-,+)(+,+,-)(-,+,-)(-,-,-)(+,-,-)卦限图卦限图?A1(1,4,0)?A(1,4,1)?(2,-2,0)
B1? B
(2,-2,-1)?(-1,-3,0)
C1?(-1,-3,3)
C练习:在空间直角坐标系中作出下列各点
(1)、A(1,4,1);
(2)、B(2,-2,-1);
(3)、C(-1,-3,3);思考3:设点M的坐标为(x,y,z)那么点M关于x轴、y轴、z轴及原点对称的点的坐标分别是什么?M(x,y,z)N(x,-y,-z)练习:规律:关于谁对称谁不变1.关于原点对称的为 (-x,-y,-z)空间直角坐标系中任一点p(x,y,z)2.关于x轴对称的为 (x,-y,-z)3.关于y轴对称的为 (-x, y,-z)4.关于z轴对称的为 (-x,-y, z)例:(1,2,3)(-1,-2,-3)(-1,-2,3)(-1,2,-3)(1,-2,-3)5.关于xoy平面对称的点为(x,y,-z)(1,2,-3)6.关于xoz平面对称的点为(x,-y,z)(1,-2,3)7.关于yoz平面对称的点为(-x,y,z)(-1,2,3)思考4:
若点A(x1,y1,z1),B(x2,y2,z2),则线段AB的中点M的坐标如何?随堂练习求下列各点的坐标1.2.3.4.思考5:点P1(x1,y1,z1)与P2(x2,y2,z2)之间的距离是
它对任意两点P1、P2都成立吗? 1. 在空间中,已知点A(1, 0, -1),B (4, 3, -1),求A、B两点之间的距离.练习: 2. 已知两点 A(-4, 1, 7)和B(3, 5, 2),点P在z轴上,若|PA|=|PB|,求点P的坐标. 3. 已知A(3,-2,-1),B(-1,-3,2),C(-5,-4,5),试判断A,B,C三点是否共线 4. 已知□ABCD的顶点A(4,1,3),B(2,-5,1),C(3,7,-5),求顶点D的坐标思考6:在空间直角坐标系中,方程 x2+y2+z2=r2(r>0为常数)表示什么图形是什么? 若r为常数,那么x2+y2+z2=r2表示以(0,0,0)为球心的球面谢谢观赏
