2.1 分解因式

课件21张PPT。第一章 第五节隆德二中 李伟第二章 分解因式1.整式乘法有几种形式?2.乘法公式有哪些?(1)单项式乘以单项式
(2)单项式乘以多项式
(3)多项式乘以多项式(1)平方差公式 (2)完全平方公式3.计算:
(1)3a(a-2b+c)
(2)(a+3)(a-3)
(3)(a+2b)2
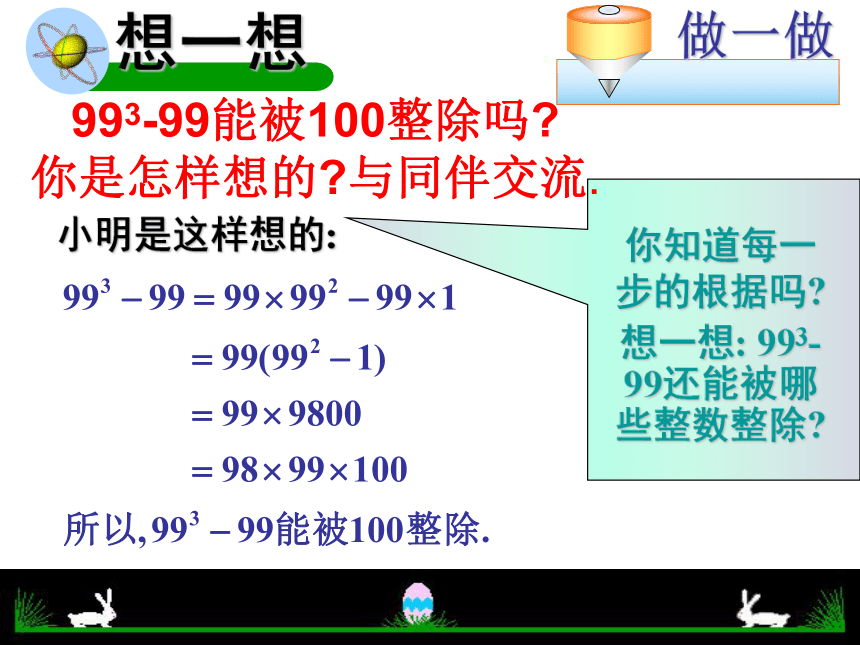
(4)(a-3b)2=3a2-6ab+3ac=a2 - 9=a2+4ab+4b2=a2-6ab+9b2数学中的游戏游戏规则：1、大家说出一个大于1的正整数。2、写出它的立方减它的式子。如：3、不通过计算，说出这个式子能被那些正整数整除。你能做到吗？小明是这样想的:993-99能被100整除吗?你是怎样想的?与同伴交流.根据左面算式填空:
(1) 3x2-3x=_________
(2)ma+mb+mc=___
(3) m2-16=__________
(4) x2-6x+9=________
(5) a3-a=___________计算下列各式:
3x(x-1)= __,
m(a+b+c) = __,
(m+4)(m-4)= __,
(x-3)2= ,
a(a+1)(a-1)= __,3x2 - 3xma+mb+mcm2 -16x2-6x+9a3-a3x(x-1)m(a+b+c)(m+4)(m-4)(x-3)2a(a+1)(a-1)想一想 由a(a+1)(a-1)得到a3-a的变形是什么运算?
由a3-a得到a(a+1)(a-1)的变形与它有什么不同?答:由a(a+1)(a-1)得到a3-a的变形是
整式乘法,由a3-a得到a(a+1)(a-1)
的变形与上面的变形互为逆过程.议一议分解因式定义: 把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式分解因式.想一想: 分解因式与整式乘法有何关系?理解 · 定义知道吗?善于辨析：分解因式与整式乘法
有什么关系?二者是互逆的恒等变形 分解因式练习一 理解概念判断下列各式哪些是整式乘法?哪些是因式分解?
(1).x2-4y2=(x+2y)(x-2y)
(2).2x(x-3y)=2x2-6xy
(3).(5a-1)2=25a2-10a+1
(4).x2+4x+4=(x+2)2
(5).(a-3)(a+3)=a2-9
(6).m2-42=(m+4)(m-4)
(7).2 πR+ 2 πr= 2 π(R+r)因式分解整式乘法整式乘法因式分解整式乘法因式分解因式分解随堂练习一P401、连一连2、在课本上。练习二 试一试把下列各式写成乘积的形式:
(1). 1-x2
(2). 4a2+4a+1
(3). 4x2-8x
(4). 2x2y-6xy2
(5). 1-4x2
(6). x2-14x+49=(1+x)(1-x)=(2a+1)2=4x(x-2)=2xy(x-3y)=(1-2x)(1+2x)=(x-7)2练习三 拓展应用 1. 计算: 7652×17－2352 ×17
解: 7652×17－2352 ×17
=17(7652 －2352)=17(765+235)(765 －235)
=17 ×1000 ×530=9010000 2. 20042+2004能被2005整除吗?
解: ∵20042+2004=2004(2004+1)
=2004 ×2005
∴ 20042+2004能被2005整除学以致用1、若 —x—m=（x+2)(x-3) 则m=_______2、若 —ax+b=能分解成（x-1)（x-4），
则a=___,b=___ 假如用一根比地球赤道长10米的铁丝将地球赤道围起来,那么铁丝与赤道之间均匀的间隙能有多大(赤道看成圆形)?异想天开真相大白R –r 规律总结分解因式与整式乘法是互逆过程.
分解因式要注意以下几点:
1.分解的对象必须是多项式.
2.分接的结果一定是几个整式
的乘积的形式.
3.要分解到不能分解为止. 阅读 ? 体验 ?作业
P40 习题2.1
1、2、3、4补充练习若a=101,b=99,求a2-b2的值.
若x=-3,求20x2-60x的值.
1993-199能被200整除吗?还能被哪些整数整除?补充练习4. 若n是整数,证明(2n+1)2-(2n-1)2是8的倍数.
5. 某工厂需加工一批零件,由甲、乙、丙三位工人共同完成，已知甲工人每天加工23个零件，乙工人每天加工19个零件，丙工人每天加工18个零件，三人需共同做12天才能做完，要加工的零件共有多少？
欢迎指导