完全平方公式（1）

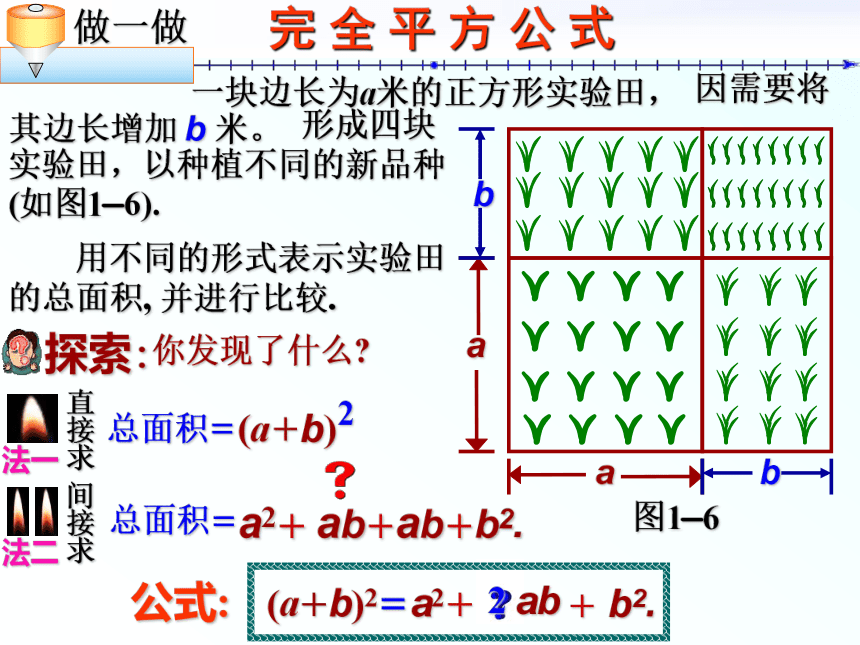
课件12张PPT。回顾与思考公式的结构特征:左边是a2 ? b2; 两个二项式的乘积,平方差公式应用平方差公式的注意事项: 对于一般两个多项式的积, 看准这两个多项式是否只含有相等的“项”和符号相反的“项”; 仅当把两个多项式的积变成公式标准形式后，才能使用平方差公式。 (a+b)(a?b)=即两数和与这两数差的积.右边是两数的平方差. 完 全 平 方 公 式 一块边长为a米的正方形实验田，图1—6 因需要将其边长增加 b 米。 形成四块实验田，以种植不同的新品种(如图1—6). 用不同的形式表示实验田的总面积, 并进行比较. (a+b) 2a2+ab+ab+b2.(a+b)2=a2+ab+b2.2 完全平方公式 (1) 你能用别的方法来说明它成立吗?(a+b)2=a2+2ab+b2 ;(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2;(2)a2 ?2ab+b2.小颖写出了如下的算式:(a?b)2=[a+(?b)]2?她是怎么想的?利用两数和的
完全平方公式
?推证公式?= 2 + 2 + 2 aa(?b)(?b)=a22ab?b2.+你能继续做下去吗?的证明标题第一章 整 式完全平方公式(1)8标题完全平方公式(a+b)2 = a2+2ab+b2 .
(a?b)2 = a2?2ab+b2 .例题解析例题 例1 利用完全平方公式计算：
(1) (2x?3)2 ； (2) (4x+5y)2 ; (3) (mn?a)2 使用完全平方公式与平方差公式的使用一样, 先把要计算的式子与完全平方公式对照, 明确哪个是 a , 哪个是 b.前者2x4x22x的平方,( )2?减去2x前后两数?2x3?乘积的2倍,?2加上+后者3的平方.2=?12x+9 ;3随堂练习 (1) ( x ? 2y)2 ；
(2) (2xy+ x )2 ;1、计算：(3) (n +1)2 ? n2.请你用几何图形直观地解释下列等式(a+b)2 = a2+2ab+b2 .
(a?b)2 = a2?2ab+b2 . 完全平方公式(a+b)2 = a2+2ab+b2 .
(a?b)2 = a2?2ab+b2 .a2abb2(a+b)2=a?ba?bab? b2(a?b)2a2+2ab+b2(a?b)2 = a2?2ab+b2纠 错 练 习 指出下列各式中的错误，并加以改正：
(1) (2a?1)2＝2a2?2a+1;
(2) (2a+1)2＝4a2 +1；
(3) (?a?1)2＝?a2?2a?1.解: (1)第一数被平方时, 未添括号;第一数与第二数乘积的2倍 少乘了一个2 ;应改为: (2a?1)2＝ (2a)2?2?2a?1+1; (2) 少了第一数与第二数乘积的2倍 (丢了一项);应改为: (2a+1)2＝ (2a)2+2?2a?1 +1; (3) 第一数平方未添括号, 第一数与第二数乘积的2倍 错了符号;第二数的平方 这一项错了符号;应改为: (?a?1)2＝(?a)2?2?(?a )?1+12; 拓 展 练 习 下列等式是否成立? 说明理由．
(1) (?4a+1)2=(1?4a)2；
(2) (?4a?1)2=(4a+1)2；
(3) (4a?1)(1?4a)＝(4a?1)(4a?1)＝(4a?1)2；
(4) (4a?1)(?1?4a)＝(4a?1)(4a+1).(1) 由加法交换律 ?4a+l＝l?4a。成立理由:(2) ∵ ?4a?1＝?(4a+1)，成立∴(?4a?1)2＝[?(4a+1)]2＝(4a+1)2.(3) ∵ (1?4a)＝?(?1+4a)不成立．即 (1?4a)＝?(4a?1)＝?(4a?1)，∴ (4a?1)(1?4a)＝(4a?1)·[?(4a?1)]＝?(4a?1)(4a?1)＝?(4a?1)2。 不成立．(4) 右边应为:?(4a?1)(4a+1)。本节课你的收获是什么？小结本节课你学到了什么?注意完全平方公式和平方差公式不同：形式不同．结果不同：完全平方公式的结果 是三项，
即 (a ?b)2＝a2 ?2ab+b2;平方差公式的结果 是两项，
即 (a+b)(a?b)＝a2?b2. 有时需要进行变形，使变形后的式子符合应用完全平方公式
的条件，即为“两数和(或差)的平方”，然后应用公式计算. 在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2；第一(二)数是乘积被平方时要注意添括号, 是运用完全平方公式进行多项式乘法的关键