第一章三角形单元测试卷(含解析)
图片预览



文档简介
〖鲁教版五四制七年级上数学单元测试卷〗
第一章《三角形》
班级: 姓名: 得分:
(时间90分钟 满分100分)
一、选择题:本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
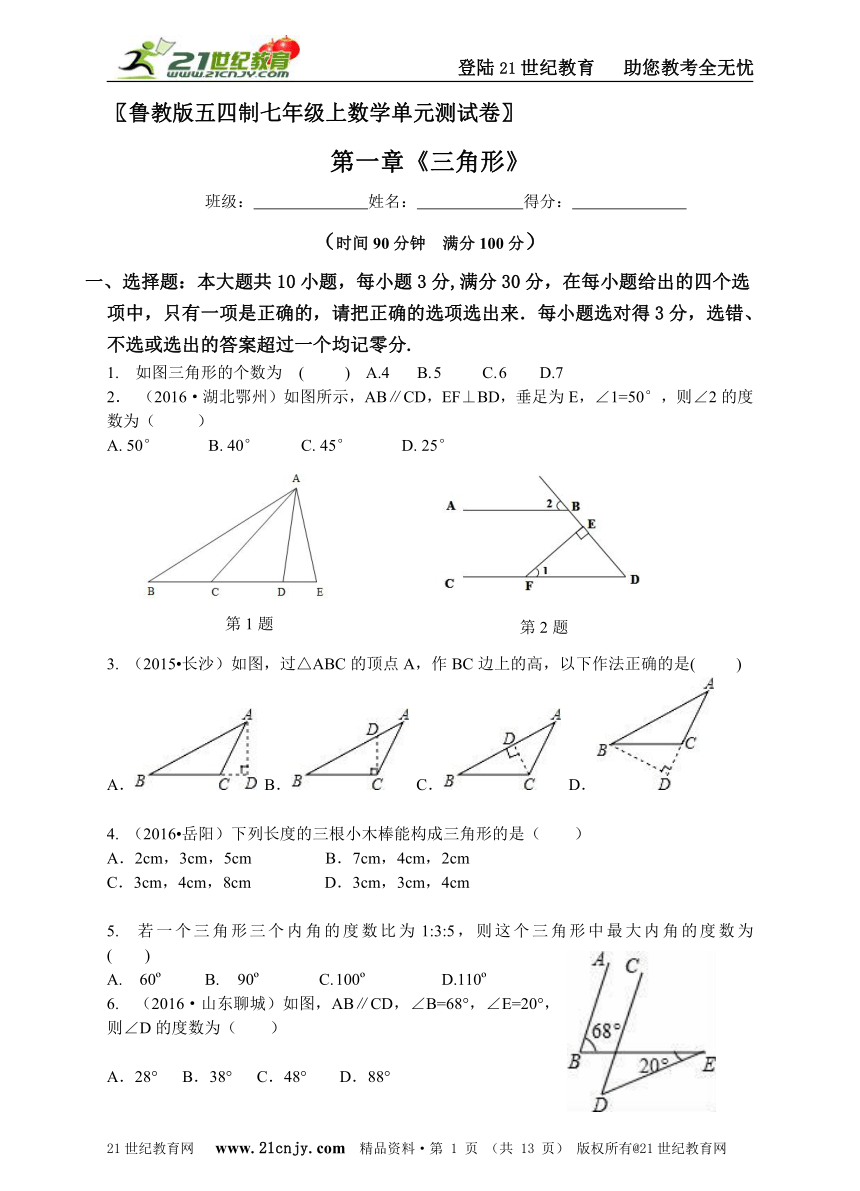
1. 如图三角形的个数为 ( ) A.4 B. 5 C. 6 D.7
2. (2016·湖北鄂州)如图所示,AB∥CD,EF⊥BD,垂足为E,∠1=50°,则∠2的度数为( )
A. 50° B. 40° C. 45° D. 25°
3. (2015?长沙)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A. B. C. D.
4. (2016?岳阳)下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm B.7cm,4cm,2cm
C.3cm,4cm,8cm D.3cm,3cm,4cm
5. 若一个三角形三个内角的度数比为1:3:5,则这个三角形中最大内角的度数为 ( )
A. 60o B. 90o C. 100o D.110o
6. (2016·山东聊城)如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38° C.48° D.88°
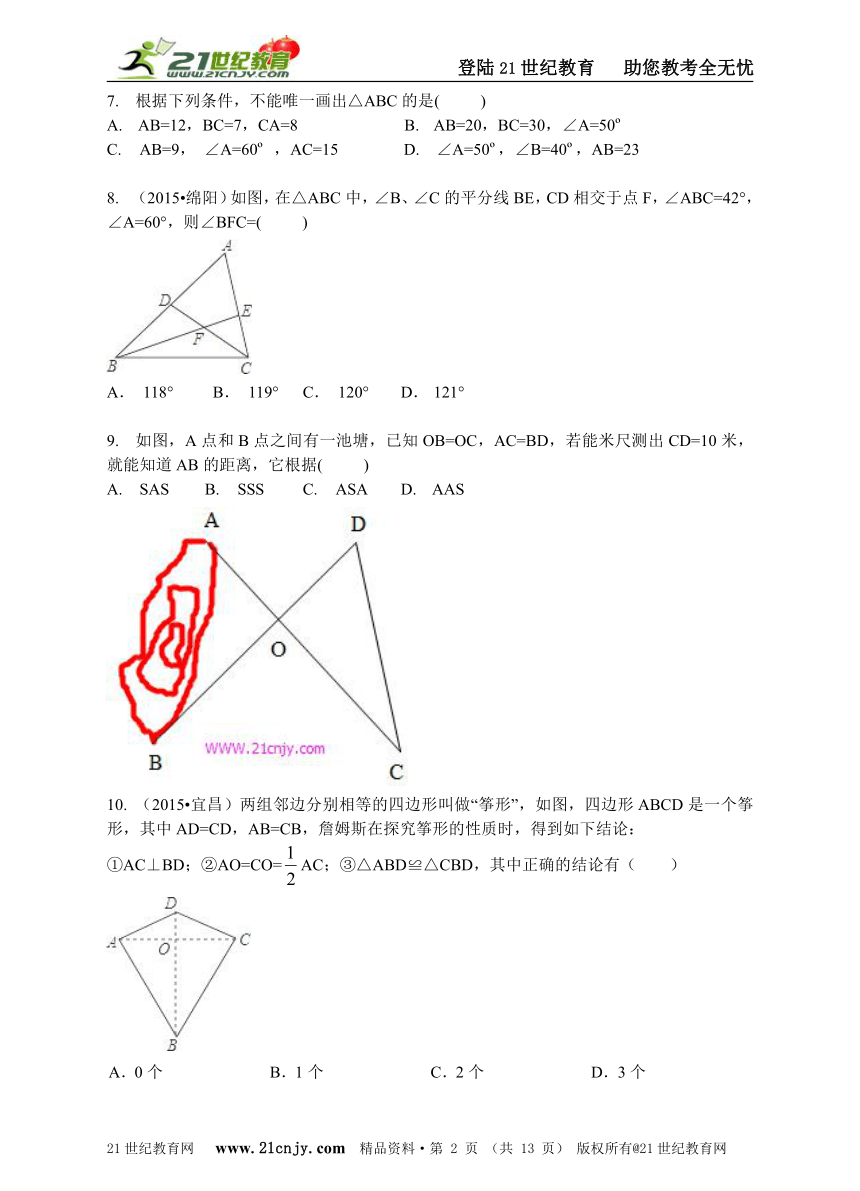
7. 根据下列条件,不能唯一画出△ABC的是( )
A. AB=12,BC=7,CA=8 B. AB=20,BC=30,∠A=50o
C. AB=9, ∠A=60o ,AC=15 D. ∠A=50o,∠B=40o,AB=23
8. (2015?绵阳)如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )
A. 118° B. 119° C. 120° D. 121°
9. 如图,A点和B点之间有一池塘,已知OB=OC,AC=BD,若能米尺测出CD=10米,就能知道AB的距离,它根据( )
A. SAS B. SSS C. ASA D. AAS
10. (2015?宜昌)两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:
①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD,其中正确的结论有( )
A.
0个
B.
1个
C.
2个
D.
3个
二、填空题(本大题共4小题,每小题4分,满分16分)
11. (2015?江苏盐城)如图,在△ABC与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需再添加的一个条件可以是 .
12. 小明家的椅子坏了, 小明在学校学习了鲁教版五四制七上数学第一章《三角形》的知识后,正在家里帮爸爸妈妈修理椅子,请你告诉大家聪明的小明应用的数学原理: 。
(2016·黑龙江大庆)如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC= .
14. 如图在△ABC中,AD是△ABC的中线,DE是△ABD的中线,若=3,则=
; = 。
三、解答题(本大题共6小题,第15、16小题每小题6分,第17、18小题每小题9分,第19、20小题每小题12分,满分54分)
15. (本题满分6分)
(2016·湖北武汉)如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:AB∥DE.
(本题满分6分)
如图,已知线段,用尺规作图画三角形△ABC,使AB=,BC=,AC=(要求:①写出作法;②保留作图痕迹)。
17.(本题满分9分)
(2016·云南省昆明市)如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB求证:AE=CE.
(本题满分9分)
如图,点A和点B分别是青云湖的南北两岸,在湖中有一测量水位的标杆点O, 湖边的游客想知道O点到湖南岸B点的距离,经过大伙讨论采用下列方法测量:(1)从北岸A点拉一条很长的绳子到F点,利用绳子找出中点C;(2)再从南岸到点C,D拉一条绳子,使BC=CD;(3)在线段DE上进行目测,使O,C,E在同一直线上,这样就确定准E点;(4)用米尺测量DE=100米。
通过上述方法你知道O点到湖南岸B点的距离了吗?请说明道理。
19. (本题满分12分)
(2015?温州)如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD.
(2)若AB=CF,∠B=30°,求∠D的度数.
(本题满分12分)
如图在Rt△ABC中,AB=AC,过A点任意作一直线m,过B点作BD⊥直线m,垂足为D,过C点作CE⊥直线m,垂足为E,若CE>BD,请思考下面两个问题:(1)AD和CE谁长谁短?请说明理由。(2)线段CE,DE,BD之间满足什么数量关系?请开动脑经探索并证明这个问题。
〖鲁教版五四制七年级上数学单元测试卷〗
第一章《三角形》答案与解析
1.【答案】:C
【解析】:数三角形时,按从左到右的顺序分类数,△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,共6个。
2.【答案】:B
【解析】:
如图,∵AB∥CD,
∴∠2=∠D;
4.【答案】:D
【解析】:依据三角形任意两边之和大于第三边求解即可.
A.因为2+3=5,所以不能构成三角形,故A错误;
B.因为2+4<6,所以不能构成三角形,故B错误;
C.因为3+4<8,所以不能构成三角形,故C错误;
D.因为3+3>4,所以能构成三角形,故D正确.
故选:D.
【点评】本题主要考查的是三角形的三边关系,掌握三角形的三边关系是解题的关键.
5.【答案】:C
【解析】:依据三角形内角和为180o,列方程求出即可。
解:设三角形三个内角的度数分别为,,,由题意得,解得=20o,所以最大的内角为100o,故选C.
6.【答案】:C
【解析】:考点平行线性质及三角形内角和定理
证明:
7.【答案】:B
【解析】:考察尺规作图的理论依据及三角形的判定方法。
依据SSS定理能画出三角形 B. 利用已知条件属于SSA,无法判定三角形全等,无法画出三角形 C.依据SAS定理能画出三角形 D.依据ASA定理能画出三角形
故选B
8.【答案】:C
【解析】:考点:三角形内角和定理.由三角形内角和定理得∠ABC+∠ACB=120°,由角平分线的性质得∠CBE+∠BCD=60°,再利用三角形的内角和定理得结果.
证明: 解:∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵BE,CD是∠B、∠C的平分线,
∴∠CBE=∠ABC,∠BCD=,
∴∠CBE+∠BCD=(∠ABC+∠BCA)=60°,
∴∠BFC=180°﹣60°=120°,
故选:C.
点评:本题主要考查了三角形内角和定理和角平分线的性质,综合运用三角形内角和定理和角平分线的性质是解答此题的关键.
9.【答案】:A
【解析】:考点利用三角形的判定定理测量距离
证明:
10.【答案】:D
【解析】:全等三角形的判定与性质.先证明△ABD与△CBD全等,再证明△AOD与△COD全等即可判断。
解答:
解:在△ABD与△CBD中,
,
∴△ABD≌△CBD(SSS),
故③正确;
∴∠ADB=∠CDB,
在△AOD与△COD中,
,
∴△AOD≌△COD(SAS),
∴∠AOD=∠COD=90°,AO=OC,
∴AC⊥DB,
故①②正确;
故选D
二、填空题
11.【答案】:DC=BC或∠DAC=∠BAC
【解析】:考点:全等三角形的判定.添加DC=BC,利用SSS即可得到两三角形全等;添加∠DAC=∠BAC,利用SAS即可得到两三角形全等.
解:添加条件为DC=BC,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS);
若添加条件为∠DAC=∠BAC,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(SAS).
故答案为:DC=BC或∠DAC=∠BAC
点评: 此题考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解本题的关键.
12.【答案】:三角形的稳定性
【解析】:考察三角形三边关系的应用性问题,三角形相对于四边形具有稳定性,在实际生活中应用广泛。
13.【答案】:110°
【解析】:考点:三角形内角和定理.由D点是∠ABC和∠ACB角平分线的交点可推出∠DBC+∠DCB=70,再利用三角形内角和定理即可求出∠BDC的度数.
证明:∵D点是∠ABC和∠ACB角平分线的交点,
∴有∠CBD=∠ABD=∠ABC,∠BCD=∠ACD=∠ACB,
∴∠ABC+∠ACB=180﹣40=140,
∴∠OBC+∠OCB=70,
∴∠BOC=180﹣70=110°,
故答案为:110°.
【点评】此题主要考查学生对角平分线性质,三角形内角和定理,三角形的外角性质等知识点的理解和掌握,难度不大,是一道基础题,熟记三角形内角和定理是解决问题的关键.
14.【答案】:6;12
【解析】:考察三角形的三线(角平分线、中线和高)
证明:
15.【答案】:AB∥DE
【解析】:全等三角形的判定和性质
证明:由BE=CF可得BC=EF,又AB=DE,AC=DF,故△ABC≌△DEF(SSS),则∠B=∠DEF,∴AB∥DE.
16.【答案】:
17.【解析】:考点全等三角形的判定与性质.根据平行线的性质得出∠A=∠ECF,∠ADE=∠CFE,再根据全等三角形的判定定理AAS得出△ADE≌△CFE,即可得出答案.
证明:∵FC∥AB,
∴∠A=∠ECF,∠ADE=∠CFE,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS),
∴AE=CE.
18.【答案】:O点到湖南岸B点的距离OB=100米。
【解析】:数学来源于生活,数学又能方便生活,此题是用全等三角形的知识进行测量距离。
证明:
19.【答案】:∠D=75°
【解析】:考点全等三角形的判定与性质.
(1)易证得△ABE≌△CDF,即可得AB=CD;
(2)易证得△ABE≌△CDF,即可得AB=CD,又由AB=CF,∠B=30°,即可证得△ABE是等腰三角形,解答即可.
证明:(1)∵AB∥CD,
∴∠B=∠C,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AB=CD;
(2)∵△ABE≌△CDF,
∴AB=CD,BE=CF,
∵AB=CF,∠B=30°,
∴AB=BE,
∴△ABE是等腰三角形,
∴∠D=.
点评: 此题考查全等三角形问题,关键是根据AAS证明三角形全等,再利用全等三角形的性质解答.
20.【答案】:(1)AD=CE;(2)CE=DE+BD
【解析】:考点三角形全等及等腰直角三角形知识,此类是探索性问题,难度大,关键是通过图形和已知条件寻找全等三角形及学会转移思路和等量代换。
第一章《三角形》
班级: 姓名: 得分:
(时间90分钟 满分100分)
一、选择题:本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1. 如图三角形的个数为 ( ) A.4 B. 5 C. 6 D.7
2. (2016·湖北鄂州)如图所示,AB∥CD,EF⊥BD,垂足为E,∠1=50°,则∠2的度数为( )
A. 50° B. 40° C. 45° D. 25°
3. (2015?长沙)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A. B. C. D.
4. (2016?岳阳)下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm B.7cm,4cm,2cm
C.3cm,4cm,8cm D.3cm,3cm,4cm
5. 若一个三角形三个内角的度数比为1:3:5,则这个三角形中最大内角的度数为 ( )
A. 60o B. 90o C. 100o D.110o
6. (2016·山东聊城)如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38° C.48° D.88°
7. 根据下列条件,不能唯一画出△ABC的是( )
A. AB=12,BC=7,CA=8 B. AB=20,BC=30,∠A=50o
C. AB=9, ∠A=60o ,AC=15 D. ∠A=50o,∠B=40o,AB=23
8. (2015?绵阳)如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )
A. 118° B. 119° C. 120° D. 121°
9. 如图,A点和B点之间有一池塘,已知OB=OC,AC=BD,若能米尺测出CD=10米,就能知道AB的距离,它根据( )
A. SAS B. SSS C. ASA D. AAS
10. (2015?宜昌)两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:
①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD,其中正确的结论有( )
A.
0个
B.
1个
C.
2个
D.
3个
二、填空题(本大题共4小题,每小题4分,满分16分)
11. (2015?江苏盐城)如图,在△ABC与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需再添加的一个条件可以是 .
12. 小明家的椅子坏了, 小明在学校学习了鲁教版五四制七上数学第一章《三角形》的知识后,正在家里帮爸爸妈妈修理椅子,请你告诉大家聪明的小明应用的数学原理: 。
(2016·黑龙江大庆)如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC= .
14. 如图在△ABC中,AD是△ABC的中线,DE是△ABD的中线,若=3,则=
; = 。
三、解答题(本大题共6小题,第15、16小题每小题6分,第17、18小题每小题9分,第19、20小题每小题12分,满分54分)
15. (本题满分6分)
(2016·湖北武汉)如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:AB∥DE.
(本题满分6分)
如图,已知线段,用尺规作图画三角形△ABC,使AB=,BC=,AC=(要求:①写出作法;②保留作图痕迹)。
17.(本题满分9分)
(2016·云南省昆明市)如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB求证:AE=CE.
(本题满分9分)
如图,点A和点B分别是青云湖的南北两岸,在湖中有一测量水位的标杆点O, 湖边的游客想知道O点到湖南岸B点的距离,经过大伙讨论采用下列方法测量:(1)从北岸A点拉一条很长的绳子到F点,利用绳子找出中点C;(2)再从南岸到点C,D拉一条绳子,使BC=CD;(3)在线段DE上进行目测,使O,C,E在同一直线上,这样就确定准E点;(4)用米尺测量DE=100米。
通过上述方法你知道O点到湖南岸B点的距离了吗?请说明道理。
19. (本题满分12分)
(2015?温州)如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD.
(2)若AB=CF,∠B=30°,求∠D的度数.
(本题满分12分)
如图在Rt△ABC中,AB=AC,过A点任意作一直线m,过B点作BD⊥直线m,垂足为D,过C点作CE⊥直线m,垂足为E,若CE>BD,请思考下面两个问题:(1)AD和CE谁长谁短?请说明理由。(2)线段CE,DE,BD之间满足什么数量关系?请开动脑经探索并证明这个问题。
〖鲁教版五四制七年级上数学单元测试卷〗
第一章《三角形》答案与解析
1.【答案】:C
【解析】:数三角形时,按从左到右的顺序分类数,△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,共6个。
2.【答案】:B
【解析】:
如图,∵AB∥CD,
∴∠2=∠D;
4.【答案】:D
【解析】:依据三角形任意两边之和大于第三边求解即可.
A.因为2+3=5,所以不能构成三角形,故A错误;
B.因为2+4<6,所以不能构成三角形,故B错误;
C.因为3+4<8,所以不能构成三角形,故C错误;
D.因为3+3>4,所以能构成三角形,故D正确.
故选:D.
【点评】本题主要考查的是三角形的三边关系,掌握三角形的三边关系是解题的关键.
5.【答案】:C
【解析】:依据三角形内角和为180o,列方程求出即可。
解:设三角形三个内角的度数分别为,,,由题意得,解得=20o,所以最大的内角为100o,故选C.
6.【答案】:C
【解析】:考点平行线性质及三角形内角和定理
证明:
7.【答案】:B
【解析】:考察尺规作图的理论依据及三角形的判定方法。
依据SSS定理能画出三角形 B. 利用已知条件属于SSA,无法判定三角形全等,无法画出三角形 C.依据SAS定理能画出三角形 D.依据ASA定理能画出三角形
故选B
8.【答案】:C
【解析】:考点:三角形内角和定理.由三角形内角和定理得∠ABC+∠ACB=120°,由角平分线的性质得∠CBE+∠BCD=60°,再利用三角形的内角和定理得结果.
证明: 解:∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵BE,CD是∠B、∠C的平分线,
∴∠CBE=∠ABC,∠BCD=,
∴∠CBE+∠BCD=(∠ABC+∠BCA)=60°,
∴∠BFC=180°﹣60°=120°,
故选:C.
点评:本题主要考查了三角形内角和定理和角平分线的性质,综合运用三角形内角和定理和角平分线的性质是解答此题的关键.
9.【答案】:A
【解析】:考点利用三角形的判定定理测量距离
证明:
10.【答案】:D
【解析】:全等三角形的判定与性质.先证明△ABD与△CBD全等,再证明△AOD与△COD全等即可判断。
解答:
解:在△ABD与△CBD中,
,
∴△ABD≌△CBD(SSS),
故③正确;
∴∠ADB=∠CDB,
在△AOD与△COD中,
,
∴△AOD≌△COD(SAS),
∴∠AOD=∠COD=90°,AO=OC,
∴AC⊥DB,
故①②正确;
故选D
二、填空题
11.【答案】:DC=BC或∠DAC=∠BAC
【解析】:考点:全等三角形的判定.添加DC=BC,利用SSS即可得到两三角形全等;添加∠DAC=∠BAC,利用SAS即可得到两三角形全等.
解:添加条件为DC=BC,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS);
若添加条件为∠DAC=∠BAC,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(SAS).
故答案为:DC=BC或∠DAC=∠BAC
点评: 此题考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解本题的关键.
12.【答案】:三角形的稳定性
【解析】:考察三角形三边关系的应用性问题,三角形相对于四边形具有稳定性,在实际生活中应用广泛。
13.【答案】:110°
【解析】:考点:三角形内角和定理.由D点是∠ABC和∠ACB角平分线的交点可推出∠DBC+∠DCB=70,再利用三角形内角和定理即可求出∠BDC的度数.
证明:∵D点是∠ABC和∠ACB角平分线的交点,
∴有∠CBD=∠ABD=∠ABC,∠BCD=∠ACD=∠ACB,
∴∠ABC+∠ACB=180﹣40=140,
∴∠OBC+∠OCB=70,
∴∠BOC=180﹣70=110°,
故答案为:110°.
【点评】此题主要考查学生对角平分线性质,三角形内角和定理,三角形的外角性质等知识点的理解和掌握,难度不大,是一道基础题,熟记三角形内角和定理是解决问题的关键.
14.【答案】:6;12
【解析】:考察三角形的三线(角平分线、中线和高)
证明:
15.【答案】:AB∥DE
【解析】:全等三角形的判定和性质
证明:由BE=CF可得BC=EF,又AB=DE,AC=DF,故△ABC≌△DEF(SSS),则∠B=∠DEF,∴AB∥DE.
16.【答案】:
17.【解析】:考点全等三角形的判定与性质.根据平行线的性质得出∠A=∠ECF,∠ADE=∠CFE,再根据全等三角形的判定定理AAS得出△ADE≌△CFE,即可得出答案.
证明:∵FC∥AB,
∴∠A=∠ECF,∠ADE=∠CFE,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS),
∴AE=CE.
18.【答案】:O点到湖南岸B点的距离OB=100米。
【解析】:数学来源于生活,数学又能方便生活,此题是用全等三角形的知识进行测量距离。
证明:
19.【答案】:∠D=75°
【解析】:考点全等三角形的判定与性质.
(1)易证得△ABE≌△CDF,即可得AB=CD;
(2)易证得△ABE≌△CDF,即可得AB=CD,又由AB=CF,∠B=30°,即可证得△ABE是等腰三角形,解答即可.
证明:(1)∵AB∥CD,
∴∠B=∠C,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AB=CD;
(2)∵△ABE≌△CDF,
∴AB=CD,BE=CF,
∵AB=CF,∠B=30°,
∴AB=BE,
∴△ABE是等腰三角形,
∴∠D=.
点评: 此题考查全等三角形问题,关键是根据AAS证明三角形全等,再利用全等三角形的性质解答.
20.【答案】:(1)AD=CE;(2)CE=DE+BD
【解析】:考点三角形全等及等腰直角三角形知识,此类是探索性问题,难度大,关键是通过图形和已知条件寻找全等三角形及学会转移思路和等量代换。
