第三章勾股定理单元测试题(含解析)
图片预览


文档简介
〖鲁教版五四制七年级上数学单元测试卷〗
第三章《勾股定理》
班级: 姓名: 得分:
(时间90分钟 满分100分)
一、选择题:本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.21世纪教育网版权所有
1. 中国古代的数学家们很早就尝试对勾股定理的证明。最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽,赵爽创制了一幅“勾股弦方图”。在图中每个直角三角形的两直角边分别是,,大正方形的面积是25,小正方形的面积是1,那么的值是( )
A. 49 B.25 C. 13 D.26
2. (2016·湖北荆门)如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )2·1·c·n·j·y
A.5 B.6 C.8 D.10
3. 已知三角形的三个内角分别是∠A,∠B,∠C,三边分别是,,,下列说法:①;②;③;③,能判定是直角三角形的是( )2-1-c-n-j-y
A. ①② B. ③④ C. ①④ D.②③
4. 已知,则以,,为边的三角形一定是( )2·1·c·n·j·y
A. 等边三角形 B. 等腰三角形 C. 直角三角形 D.形状无法确定
5. 如图,观光塔是潍坊市区的标志性建筑,吸引美丽的喜鹊前来欣赏,聪明的小喜鹊从建筑物AB的顶端B点飞到观光塔的低端D点,估算飞行了26米,又从建筑物AB的底端A点飞到观光塔的CD顶端C点,估算飞行了30米;若已知建筑物AB高度是10米,小喜鹊心中就盘算出了观光塔CD的高度,然后高高兴兴地飞回家告诉妈妈这个小秘密。那么,小喜鹊算出观光塔CD的高度是( )米。 21*cnjy*com
18米 B. 19米 C. 20米 D.21米
6. CD是Rt△ABC斜边AB上的高,若AB=26,AC:BC=12:5,则CD为( )
A. B. C. D.
如图,在网格中,小正方形的边长是1,点A、点B、点C都在网格图的格点上,则∠ACB的度数为( )【来源:21·世纪·教育·网】
30o B. 45o C. 60o D. 75o
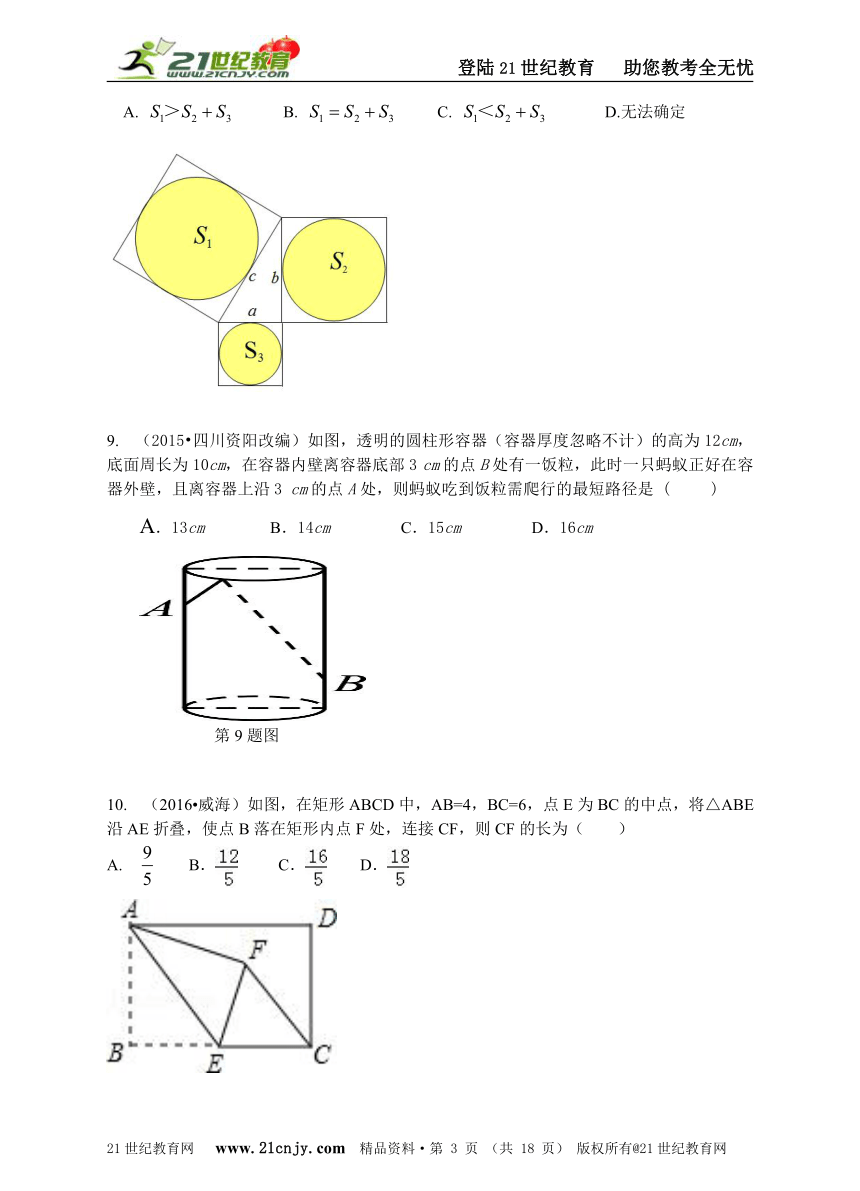
8. 如图直角三角形的三边分别是,,,且,分别以,,为边画正方形,然后再在三个正方形的内部,分别以,,为直径画圆,若三个圆的面积分别为,,,那么三个圆的面积大小关系是( )【来源:21cnj*y.co*m】
A. B. C. D.无法确定
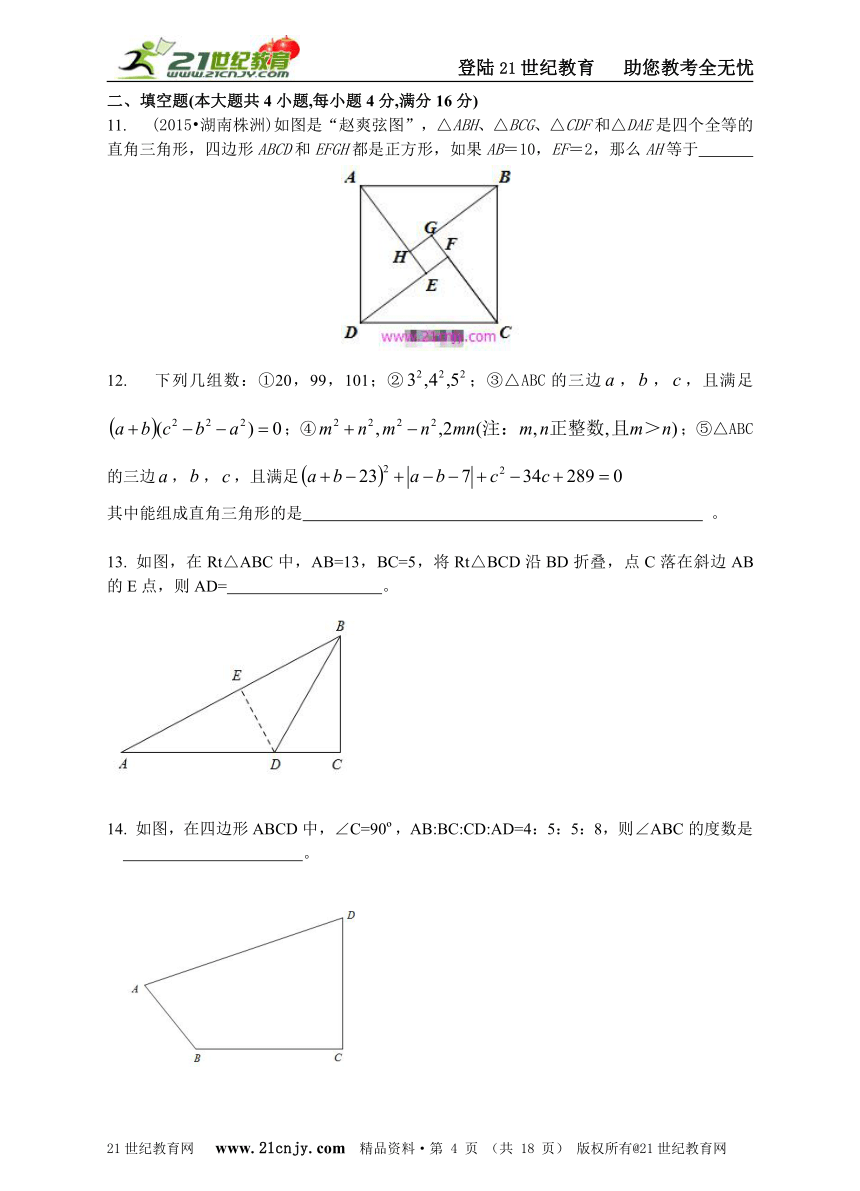
9. (2015?四川资阳改编)如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3 cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是 ( ) A.13cm B.14cm C.15cm D.16cm
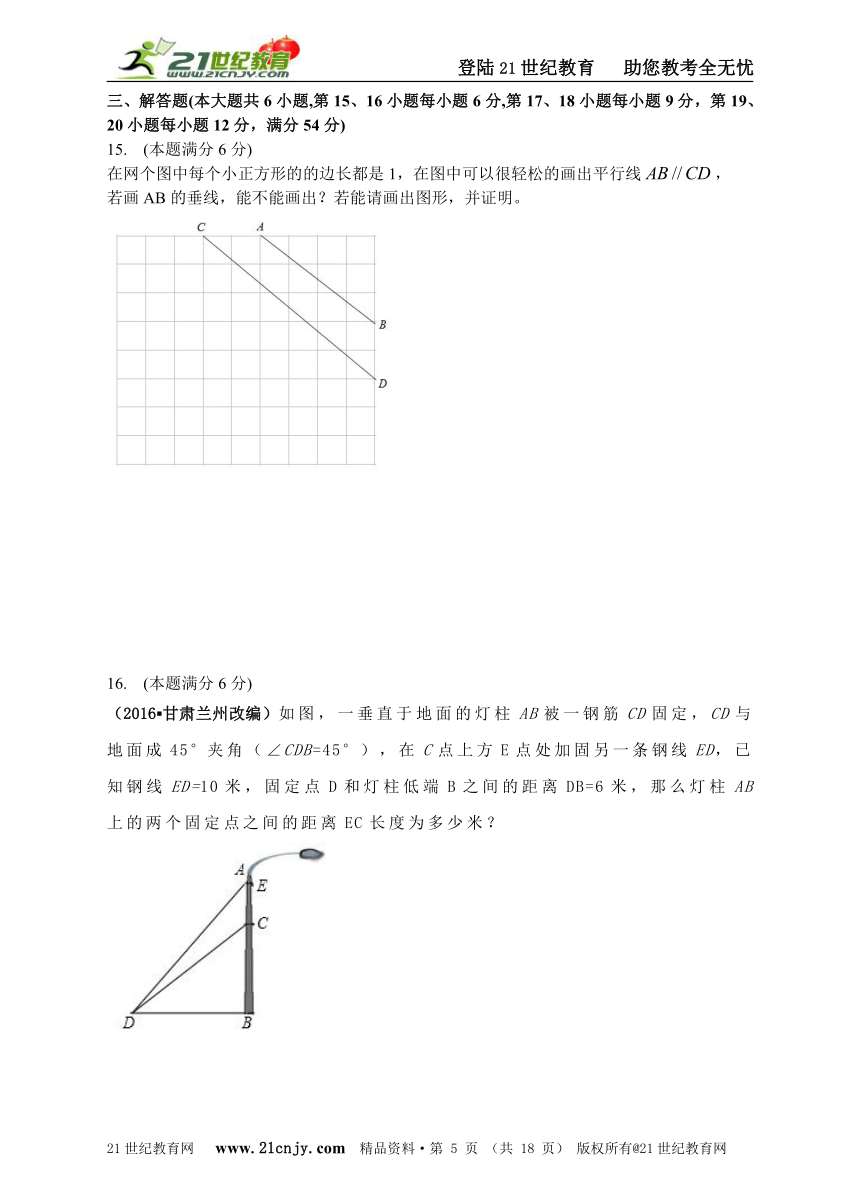
10. (2016?威海)如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题4分,满分16分)
11. (2015?湖南株洲)如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于
12. 下列几组数:①20,99,101;②;③△ABC的三边,,,且满足;④;⑤△ABC的三边,,,且满足
其中能组成直角三角形的是 。
13. 如图,在Rt△ABC中,AB=13,BC=5,将Rt△BCD沿BD折叠,点C落在斜边AB的E点,则AD= 。www.21-cn-jy.com
如图,在四边形ABCD中,∠C=90o,AB:BC:CD:AD=4:5:5:8,则∠ABC的度数是
。
三、解答题(本大题共6小题,第15、16小题每小题6分,第17、18小题每小题9分,第19、20小题每小题12分,满分54分)21·世纪*教育网
15. (本题满分6分)
在网个图中每个小正方形的的边长都是1,在图中可以很轻松的画出平行线,
若画AB的垂线,能不能画出?若能请画出图形,并证明。
16. (本题满分6分)
(2016?甘肃兰州改编)如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方E点处加固另一条钢线ED,已知钢线ED=10米,固定点D和灯柱低端B之间的距离DB=6米,那么灯柱AB上的两个固定点之间的距离EC长度为多少米?【出处:21教育名师】
17. (本题满分9分)
观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…,a,b,c
根据你发现的规律,请写出
当a=19时,求b、c的值.
当a=2n+1时,求b、c的值.
用(2)的结论判断15,111,112是否为一组勾股数,并说明理由.
(本题满分9分)
如图,小猴在距河边10米的A点玩耍,河边栽满了很多桃树,小猴家在B点,小猴A点和房子B点的东西距离是42米,南北距离是20米,突然小猴接到妈妈的电话:要求小猴迅速到河边多摘些桃子,然后再回家吃饭,请你帮助聪明的小猴设计路线,画出图形并求出小猴行驶最短距离。【版权所有:21教育】
19. (本题满分12分)
(2016西宁)如图8,已知正方形的边长为,,分别是,边上的点,且.将绕点逆时针旋转,得到.若,求的长。21教育名师原创作品
20. (本题满分12分)
(2016山东?淄博改编)如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,如果以GH为边作正方形,请求出正方形的面积。21*cnjy*com
〖鲁教版五四制七年级上数学单元测试卷〗
第一章《三角形》答案与解析
【解析】:考点 勾股定理;等腰三角形的性质.根据等腰三角形的性质得到AD⊥BC,BD=CD,根据勾股定理即可得到结论.21教育网
解:∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,BD=CD,
∴
∵AB=5,AD=3,
∴
∴BD=4,
∴BC=2BD=8,
故选C.
3.【答案】:D
【解析】:考点 勾股数及勾股定理
解:A.,不能构成直角三角形,故选项错误;
B. 设,,能构成直角三角形,故选项正确;
C. ,,能构成直角三角形,故选项正确;
D.,,不能构成直角三角形,故选项错误;
4.【答案】:C
【解析】:考点 勾股定理逆定理及完全平方公式。
解:
5.【答案】:A
【解析】:考点 勾股定理的应用
解:
6.【答案】:D
【解析】:解:考点 勾股定理及三角形面积
7.【答案】:B
【解析】:考点 勾股定理逆定理的应用
解:
8.【答案】:B
【解析】:考点 圆的面积计算及勾股定理
解:
9.【答案】:
【解析】:考点 平面展开-最短路径问题.
分析 将容器侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求. www-2-1-cnjy-com
解:如图
∵高为12cm,底面周长为16cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,
∴A′D=5cm,BD=12﹣3+AE=12cm,
∴将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,
故选:A.
点评:本题考查了平面展开﹣﹣﹣最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
10.【答案】:D
【解析】:考点 翻折变换;矩形的性质;勾股定理.
二、填空题
11.【答案】:6
【解析】:考点 全等三角形的对应边相等,直角三角形的勾股定理,正方形的边长相等;
解:由全等可知:AH=DE,AE=AH+HE
由直角三角形可得:,代入可得
答案为:6
12.【答案】:①③④⑤
【解析】:勾股定理逆定理、完全平方公式及非负式
解:
①,能构成直角三角形;
②,不能构成直角三角形;
③ ,能构成直角三角形;
④
能构成直角三角形;
⑤
14.【答案】:135o
【解析】:考点 勾股定理逆定理及应用
解:
三、解答题
15.【答案】:如图
【解析】:考点 勾股定理及逆定理
解:
16.【答案】:2米
【解析】:考点 勾股定理及解直角三角形的应用
解:
17.【答案】:(1)b=180,c=181(2)b=,a=(3)不是
【解析】:考点 勾股数及探索规律
解:(1)b=180,c=181
(2)通过观察知b-a=1,又(2n+1)2+a2=b2 ∴b2-a2=(2n+1)2
(b+a)(b-a)=(2n+1)2 ∴b+a=(2n+1)2
∴b=,a=
(3)由(2)知,2n+1,=2n(n+1),=2n(n+1)+1为一组勾股数,当n=7时,2n+1=15,112-111=1,但2n(n+1)=2×7×8=112≠111,∴15,111,112不是一组勾股数21cnjy.com
18.【答案】:路线如图,最短距离是58米
【解析】:考点 勾股定理及最短路线问题
解:设计方法:过A点作关于河边m的对称点C,连接CB交河边m于点D,连接AD、DB,则最短路线是A→D→B21·cn·jy·com
过B做BE⊥CE,垂足为E
在直角三角形CEB中,EB=42,AE=20,AF=10
∵点A和点C关于河边m对称
∴AF=CF=10,AD=CD
∴EC=AE+AF+CF=40,
由勾股定理知:
∴BC=58
∴AD+BD=BC=58
即最短距离是58米。
19.【答案】:
【解析】:考点 全等三角形、勾股定理及旋转问题
解:
第三章《勾股定理》
班级: 姓名: 得分:
(时间90分钟 满分100分)
一、选择题:本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.21世纪教育网版权所有
1. 中国古代的数学家们很早就尝试对勾股定理的证明。最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽,赵爽创制了一幅“勾股弦方图”。在图中每个直角三角形的两直角边分别是,,大正方形的面积是25,小正方形的面积是1,那么的值是( )
A. 49 B.25 C. 13 D.26
2. (2016·湖北荆门)如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )2·1·c·n·j·y
A.5 B.6 C.8 D.10
3. 已知三角形的三个内角分别是∠A,∠B,∠C,三边分别是,,,下列说法:①;②;③;③,能判定是直角三角形的是( )2-1-c-n-j-y
A. ①② B. ③④ C. ①④ D.②③
4. 已知,则以,,为边的三角形一定是( )2·1·c·n·j·y
A. 等边三角形 B. 等腰三角形 C. 直角三角形 D.形状无法确定
5. 如图,观光塔是潍坊市区的标志性建筑,吸引美丽的喜鹊前来欣赏,聪明的小喜鹊从建筑物AB的顶端B点飞到观光塔的低端D点,估算飞行了26米,又从建筑物AB的底端A点飞到观光塔的CD顶端C点,估算飞行了30米;若已知建筑物AB高度是10米,小喜鹊心中就盘算出了观光塔CD的高度,然后高高兴兴地飞回家告诉妈妈这个小秘密。那么,小喜鹊算出观光塔CD的高度是( )米。 21*cnjy*com
18米 B. 19米 C. 20米 D.21米
6. CD是Rt△ABC斜边AB上的高,若AB=26,AC:BC=12:5,则CD为( )
A. B. C. D.
如图,在网格中,小正方形的边长是1,点A、点B、点C都在网格图的格点上,则∠ACB的度数为( )【来源:21·世纪·教育·网】
30o B. 45o C. 60o D. 75o
8. 如图直角三角形的三边分别是,,,且,分别以,,为边画正方形,然后再在三个正方形的内部,分别以,,为直径画圆,若三个圆的面积分别为,,,那么三个圆的面积大小关系是( )【来源:21cnj*y.co*m】
A. B. C. D.无法确定
9. (2015?四川资阳改编)如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3 cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是 ( ) A.13cm B.14cm C.15cm D.16cm
10. (2016?威海)如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题4分,满分16分)
11. (2015?湖南株洲)如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于
12. 下列几组数:①20,99,101;②;③△ABC的三边,,,且满足;④;⑤△ABC的三边,,,且满足
其中能组成直角三角形的是 。
13. 如图,在Rt△ABC中,AB=13,BC=5,将Rt△BCD沿BD折叠,点C落在斜边AB的E点,则AD= 。www.21-cn-jy.com
如图,在四边形ABCD中,∠C=90o,AB:BC:CD:AD=4:5:5:8,则∠ABC的度数是
。
三、解答题(本大题共6小题,第15、16小题每小题6分,第17、18小题每小题9分,第19、20小题每小题12分,满分54分)21·世纪*教育网
15. (本题满分6分)
在网个图中每个小正方形的的边长都是1,在图中可以很轻松的画出平行线,
若画AB的垂线,能不能画出?若能请画出图形,并证明。
16. (本题满分6分)
(2016?甘肃兰州改编)如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方E点处加固另一条钢线ED,已知钢线ED=10米,固定点D和灯柱低端B之间的距离DB=6米,那么灯柱AB上的两个固定点之间的距离EC长度为多少米?【出处:21教育名师】
17. (本题满分9分)
观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…,a,b,c
根据你发现的规律,请写出
当a=19时,求b、c的值.
当a=2n+1时,求b、c的值.
用(2)的结论判断15,111,112是否为一组勾股数,并说明理由.
(本题满分9分)
如图,小猴在距河边10米的A点玩耍,河边栽满了很多桃树,小猴家在B点,小猴A点和房子B点的东西距离是42米,南北距离是20米,突然小猴接到妈妈的电话:要求小猴迅速到河边多摘些桃子,然后再回家吃饭,请你帮助聪明的小猴设计路线,画出图形并求出小猴行驶最短距离。【版权所有:21教育】
19. (本题满分12分)
(2016西宁)如图8,已知正方形的边长为,,分别是,边上的点,且.将绕点逆时针旋转,得到.若,求的长。21教育名师原创作品
20. (本题满分12分)
(2016山东?淄博改编)如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,如果以GH为边作正方形,请求出正方形的面积。21*cnjy*com
〖鲁教版五四制七年级上数学单元测试卷〗
第一章《三角形》答案与解析
【解析】:考点 勾股定理;等腰三角形的性质.根据等腰三角形的性质得到AD⊥BC,BD=CD,根据勾股定理即可得到结论.21教育网
解:∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,BD=CD,
∴
∵AB=5,AD=3,
∴
∴BD=4,
∴BC=2BD=8,
故选C.
3.【答案】:D
【解析】:考点 勾股数及勾股定理
解:A.,不能构成直角三角形,故选项错误;
B. 设,,能构成直角三角形,故选项正确;
C. ,,能构成直角三角形,故选项正确;
D.,,不能构成直角三角形,故选项错误;
4.【答案】:C
【解析】:考点 勾股定理逆定理及完全平方公式。
解:
5.【答案】:A
【解析】:考点 勾股定理的应用
解:
6.【答案】:D
【解析】:解:考点 勾股定理及三角形面积
7.【答案】:B
【解析】:考点 勾股定理逆定理的应用
解:
8.【答案】:B
【解析】:考点 圆的面积计算及勾股定理
解:
9.【答案】:
【解析】:考点 平面展开-最短路径问题.
分析 将容器侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求. www-2-1-cnjy-com
解:如图
∵高为12cm,底面周长为16cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,
∴A′D=5cm,BD=12﹣3+AE=12cm,
∴将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,
故选:A.
点评:本题考查了平面展开﹣﹣﹣最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
10.【答案】:D
【解析】:考点 翻折变换;矩形的性质;勾股定理.
二、填空题
11.【答案】:6
【解析】:考点 全等三角形的对应边相等,直角三角形的勾股定理,正方形的边长相等;
解:由全等可知:AH=DE,AE=AH+HE
由直角三角形可得:,代入可得
答案为:6
12.【答案】:①③④⑤
【解析】:勾股定理逆定理、完全平方公式及非负式
解:
①,能构成直角三角形;
②,不能构成直角三角形;
③ ,能构成直角三角形;
④
能构成直角三角形;
⑤
14.【答案】:135o
【解析】:考点 勾股定理逆定理及应用
解:
三、解答题
15.【答案】:如图
【解析】:考点 勾股定理及逆定理
解:
16.【答案】:2米
【解析】:考点 勾股定理及解直角三角形的应用
解:
17.【答案】:(1)b=180,c=181(2)b=,a=(3)不是
【解析】:考点 勾股数及探索规律
解:(1)b=180,c=181
(2)通过观察知b-a=1,又(2n+1)2+a2=b2 ∴b2-a2=(2n+1)2
(b+a)(b-a)=(2n+1)2 ∴b+a=(2n+1)2
∴b=,a=
(3)由(2)知,2n+1,=2n(n+1),=2n(n+1)+1为一组勾股数,当n=7时,2n+1=15,112-111=1,但2n(n+1)=2×7×8=112≠111,∴15,111,112不是一组勾股数21cnjy.com
18.【答案】:路线如图,最短距离是58米
【解析】:考点 勾股定理及最短路线问题
解:设计方法:过A点作关于河边m的对称点C,连接CB交河边m于点D,连接AD、DB,则最短路线是A→D→B21·cn·jy·com
过B做BE⊥CE,垂足为E
在直角三角形CEB中,EB=42,AE=20,AF=10
∵点A和点C关于河边m对称
∴AF=CF=10,AD=CD
∴EC=AE+AF+CF=40,
由勾股定理知:
∴BC=58
∴AD+BD=BC=58
即最短距离是58米。
19.【答案】:
【解析】:考点 全等三角形、勾股定理及旋转问题
解:
