1.1 动量定律 1.2 动量守恒定律 课件
文档属性
| 名称 | 1.1 动量定律 1.2 动量守恒定律 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 283.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-08-25 16:39:51 | ||
图片预览











文档简介
课件33张PPT。 第一节 动量定律
第二节 动量守恒定律知识点 1 物体的碰撞1.历史上对碰撞问题的研究 最早发表有关碰撞问题研究成果的是物理学家马尔西教
授,他在 1639 年发表的著作《运动的比例》中得出了一些碰撞
的结论.随后伽利略、马略特、牛顿、笛卡尔、惠更斯等都先
后做了一些实验,总结出碰撞的规律,奠定了动量守恒的基础. 近现代通过加速器技术研究高能粒子的碰撞,产生了一种
全新的基本粒子研究手段.绝大多数粒子都是在粒子的碰撞中
发现的,当代物理离不开碰撞.2.生活中的各种碰撞现象碰撞的种类有正碰和斜碰两种. (1)正碰:像台球的碰撞中若两个小球碰
撞时的速度沿着连心线方向,则称为正碰.如
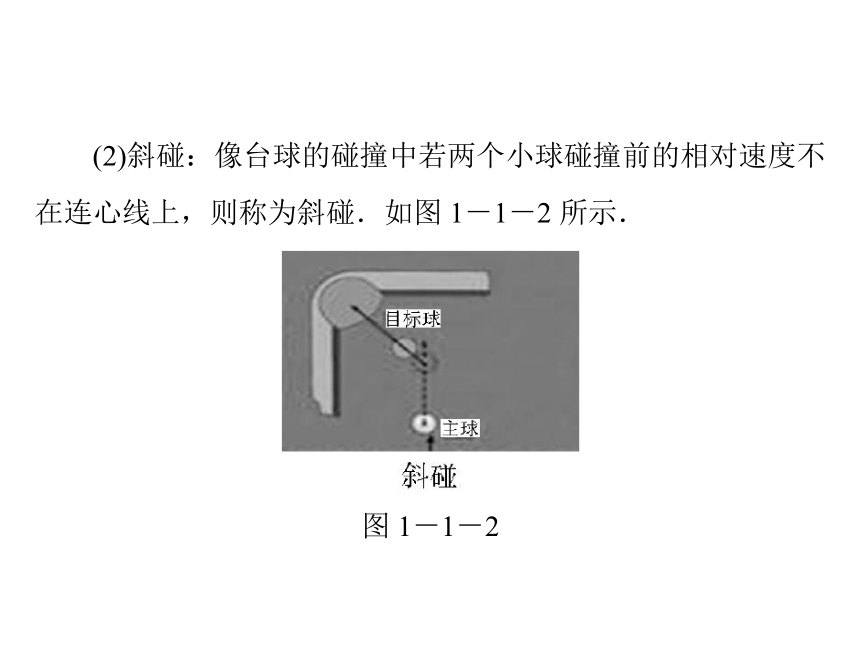
图 1-1-1 所示.图 1-1-1(2)斜碰:像台球的碰撞中若两个小球碰撞前的相对速度不在连心线上,则称为斜碰.如图 1-1-2 所示.图 1-1-23.弹性碰撞和非弹性碰撞(1)碰撞分为_________和_________撞两种. ①弹性碰撞:若两个物体的碰撞发生在水平面上,碰撞后
______________,则没有动能损失,碰撞前后两个物体构成的
系统动能相等. ②非弹性碰撞:若两个物体的碰撞发生在水平面上,碰撞
后________________或_________________,则有动能损失(或
损失最大),损失的动能转变为热能,碰撞前后两个物体构成的
系统动能不再相等,碰撞后的总动能小于碰撞前的总动能.弹性碰撞非弹性碰形变能完全恢复形变不能完全恢复完全不能恢复(黏合)(2)两种碰撞的区别:弹性碰撞没有能量损失,非弹性碰撞有能量损失. 当两个小球的碰撞发生在水平面上时,两小球碰撞前后的
重力势能不变,变化的是动能,根据动能是否守恒,把小球的
碰撞分为弹性碰撞和非弹性碰撞,如下所示:(3)注意. ①非弹性碰撞一定有机械能损失,损失的机械能一般转化
为内能.碰撞后的总机械能不可能增加,这一点尤为重要.
②系统发生爆炸时,内力对系统内的每一个物体都做正功,
故爆炸时,系统的机械能是增加的,这一增加的机械能来源于
炸药贮存的化学能.知识点 2 动量 动量守恒定律
1.动量及其变化 (1)冲量:物体受到的__与________________的乘积叫做这
个力的冲量.单位为 N·s,是一个矢量,用符号 I 表示,即 I=
Ft.冲量的方向就是力的方向. (2)动量:运动物体的____和它的____的乘积叫做这个物体
的动量.单位为 kg·m/s,是一个矢量,用符号 p 表示,即 p=
mv.动量的方向是物体运动的方向,也就是速度的方向.力这个力的作用时间质量速度(3)动量定理:合外力的冲量等于系统的动量变化量.表达式为 Ft=mvt-mv0. ①冲量的方向和动量变化量的方向是同一个方向,也是力
的方向(或是加速度的方向),冲量的方向与动量的方向不一定
相同(相同、相反,或是成某一个角度).②求某一个力的冲量有两种方法:一是用冲量的定义式 I=Ft;二是用动量定理 I=mvt- mv0.③求动量的变化量有两种方法:一是用动量变化量的定义式Δp=mvt-mv0;二是用动量定理Δp=Ft.(4)应用动量定理.
①对动量定理的理解 a.动量定理给出了状态量动量 p 和过程量冲量 I 之间的关
系,在合外力为恒力的情况下,用冲量Δp=Ft 来求物体的动量
变化量比较方便;在合外力为变力的情况下,用动量变化量的定义式Δp=mvt-mv0 来求物体的动量变化量较为方便.
b.动量定理的研究对象可以是一个物体,也可以是几个物
体组成的系统.由于系统内力的总冲量一定是零,不会改变系
统的总动量,所以对一个系统而言,“合外力的冲量等于系统
的动量变化”仍然成立. c.如果物体的运动分为几个阶段,既可以分阶段用动量定
理,也可以对全过程用动量定理.对全过程而言,把各个阶段
的冲量分别计算出来,再求其矢量和,即为物体受到的总冲量.
d.对竖直方向的打击和碰撞问题,合外力应该是撞击力和
重力的合力,不能随意忽略重力.只有在作用时间极短,撞击
力远大于重力时,重力才可以忽略不计.(5)F-t 图象中面积的物理意义. F-t 图象中的面积代表这个力的冲量.无论力是恒力还是
变力,当这个力为合外力时,F-t 图象中的面积始终代表物体
受到的冲量,等于物体的动量变化量.2.一维碰撞中的动量守恒定律 (1)系统:当两个物体相互碰撞时,这两个物体之间发生了
相互作用,把具有相互作用的这两个物体称为系统.
(2)内力和外力:________的其他物体对系统的作用力叫做外力;_________物体之间相互作用的力称为内力. (3)动量守恒定律:当一个系统所受到的__________时,系
统的_______________,这就是一维碰撞中的动量守恒定律.(4)表达式:m1v10+m2v20=m1v1+m2v2. (5)注意:动量守恒定律并不限于两个物体的相互作用,一
个系统可以包括任意数目的物体,只要整个系统受到的合外力
等于零,系统的总动量就守恒.系统外部系统内部合外力为零总动量保持不变vt-v0知识点 3 力的两大积累效应
1.力对时间的积累:I=Ft
根据牛顿第二定律:F=ma
得到 F=ma=mt,即:Ft=mvt-mv0 这就是动量定理.当合外力的__________时,很显然____
_____________,即总动量不变,这就是动量守恒定律.冲量等于零动量的变化量为零2.力对空间的积累效应:W=Fs
根据牛顿第二定律:F=mamvt-mv0【例题】人从高处跳到低处时,为了安全,一般都让脚尖先着地,这样做是为了()CA.减小冲量
B.减小动量的变化量
C.增大与地面的作用时间,从而减小冲力
D.增大人对地面的压强,起到安全作用解析:根据动量定理,F=t,脚尖先着地,增加了脚与地面的作用时间,在动量变化量一定的情况下,脚与地面
的作用力变小,起到保护作用.1.一对作用力与反作用力做的总功为 W,总冲量为 I,下列说法正确的是()A.W 一定等于零,I 不一定等于零
B.W 可能不等于零,I 一定等于零
C.W 和 I 一定都等于零
D.W 和 I 可能都不等于零 解析:一对作用力与反作用力中的两个力,既可以都做正
功(比如爆炸),也可以都做负功(比如相向运动发生碰撞而静止
的问题),也可以一个做正功,一个做负功(比如滑块在木板上
移动的问题),所以总功可能不等于零;但作用力与反作用力的
大小相等方向相反,作用时间相等,其总冲量必然等于零,只
有 B 正确.答案:B 2.(双选)从水平地面上方同一高度处,使 a 球竖直上抛,
使 b 球平抛,且两球质量相等,初速度大小相同,最后落于同一水平地面上(空气阻力不计).下列说法中正确的是()A.两球着地时的动量相同BD B.两球着地时的动能相同
C.重力对两球的冲量相同
D.重力对两球所做的功相同
解析:a、b 两球的重力相同,落下的高度相同,所以做功
相同;a、b 两球的飞行时间不同,所以重力的冲量不同.BD
正确,AC 错.知识点 4 动量守恒定律
1.动能和动量大小的换算(2)动量守恒定律成立的条件.①系统不受外力或者所受外力之和为零.②系统受外力,但外力远小于内力,可以忽略不计.
③系统在某一个方向上所受的合外力为零,则该方向上动量守恒.④全过程的某一阶段系统受的合外力为零,则该阶段系统动量守恒. 【例题】如图 1-1-3 所示的装置中,木块 B 与水平桌面
间的接触面是光滑的,子弹 A 沿水平方向射入木块后留在木块
内,将弹簧压缩到最短.现将子弹、木块和弹簧合在一起作为
研究对象(系统),则此系统在从子弹开始射入木块到弹簧压缩至最短的整个过程中( )
图 1-1-3A.动量守恒、机械能守恒B.动量不守恒、机械能不守恒
C.动量守恒、机械能不守恒
D.动量不守恒、机械能守恒 解析:若以子弹、木块和弹簧合在一起作为研究对象(系统),从
子弹开始射入木块到弹簧压缩至最短时,弹簧固定端墙壁对弹簧有外
力作用,因此动量不守恒.而在子弹射入木块时,存在剧烈摩擦作用,
有一部分能量转化为内能,机械能也不守恒.实际上,在子弹射入木
块这一瞬间过程,取子弹与木块为系统则可认为动量守恒(此瞬间弹
簧尚未形变).子弹射入木块与木块达到相同速度后压缩弹簧过程中,
机械能守恒,但动量不守恒.答案:B 3.两只小船逆向航行,航线邻近.在两船首尾相齐时,由
每只船上各自向对方放置一质量为 m=50 kg 的麻袋,结果载重
较小的船停了下来,另一船则以 v=8.5 m/s 的速度沿原方向航行.
设两只船及船上载重量分别为 m1=500 kg,m2=1 000 kg.问交
换麻袋前各船的速率是多大?(水的阻力不计) 解:每只船向对方放置麻袋过程中不会影响本船的速度,
船速之所以发生变化,是接受了对方的麻袋并与之发生相互作
用的结果.若选抛出麻袋后的此船与彼船扔来的麻袋所组成的
系统为研究对象,在水的阻力不计的情况下,系统动量守恒.
分别以各船原航行方向为正方向,则对轻船系统有(m1-m)v1-mv2=0 ①
即(500-50)v1-50v2=0对重船系统有(m2-m)v2-mv1=(m2-m+m)v ②
即(1 000-50)v2-50v1=1 000×8.5
解之可得:v1=1 m/s,v2=9 m/s.题型 1动量的矢量性与动能的标量性【例题】关于物体的动量和动能,下列说法中正确的是( )
A.一物体的动量不变,其动能一定不变
B.一物体的动能不变,其动量一定不变
C.两物体的动量相等,其动能一定相等
D.两物体的动能相等,其动量一定相等 解析:物体的动量不变实质就是速度不变,亦即速度大小
和方向均不变,所以其动能一定不变,A 对;而动能是标量,
动能不变,速度的方向是可以变化的,故其动量可以变化,B有关,又与物体的速度有关,两个物体的质量不一定相等,速
度也不一定相等,所以其动量与动能不一定相等,C、D 都错.答案:A化取决于合外力做的功,若合外力的总功不为零,动能必然变
化,若合外力的总功为零,动能必然不变;动量是矢量,表达式为 p=mv,动量是否变化取决于合外力的冲量,当合外力的冲量为零时,动量不变,当合外力的冲量不为零时,动量必然
改变.当物体的速度大小不变只是方向改变时,合外力的总功
为零,但合外力的冲量不为零,其动能是不变的,但动量的方
向必然改变. 1.(双选)一个质量为 2 kg 的物体以 2 m/s 的速度向东运动,
某时刻受到一个向西的力,过一段时间,该物体向西运动,当)其速度也为 2 m/s 时,下列说法正确的是(
A.动量变化 8 kg·m/s,向东
B.动量变化 8 kg·m/s,向西
C.动能变化为 8 J
D.动能变化为零 解析:动量是矢量,所以物体向西运动的动量 4 kg·m/s 与
向东运动时的动量 4 kg·m/s 虽然大小相同,但方向不同,所以
动量变化动量变化 8 kg·m/s,向西;动能是标量,所以未变.
BD 正确,AC 错.答案:BD题型 2动量守恒定律的简单应用 【例题】质量为 M 的小车在光滑的水平地面上以 v0 匀速运
动,当车中的沙子从底部的漏斗中不断流下时,车子速度将()BA.减小B.不变C.增大D.无法确定 解析:动量守恒的条件是合外力等于零,在沙子没有落地
之前,落下的沙子和小车组成的系统水平方向不受其他外力作
用,合外力等于零,动量守恒.在沙子没有落地之前,沙子在
水平方向和小车具有相同的速度(惯性),故小车的速度不变. 规律总结:此类问题属系统所受外力不为零,竖直方向上
受到外力,动量不守恒,但水平方向上不受外力作用,动量守
恒.又如大炮在以倾角发射炮弹时,炮身要后退,受到地面的阻
力,但因其炸药产生的作用力很大,远大于受到的阻力,故仍
认为水平方向动量守恒.在本题中,沙子未落到地面之前,沙子
的沿水平方向的速度大小不变,是解决本题的关键. 2.在光滑水平直路上停着一辆较长的木板车,车的左端站
立一个大人,车的右端站立一个小孩.如果大人向右走,小孩(质
量比大人小)向左走,他们的速度大小相同,则在他们走动过程中()BA.车可能向右运动
C.车可能保持静止B.车一定向左运动
D.无法确定 解析:系统动量守恒,他们的速度大小相同方向相反,必
有大人的动量大,故小孩和车的动量与大人的动量大小相等,
方向相反.
第二节 动量守恒定律知识点 1 物体的碰撞1.历史上对碰撞问题的研究 最早发表有关碰撞问题研究成果的是物理学家马尔西教
授,他在 1639 年发表的著作《运动的比例》中得出了一些碰撞
的结论.随后伽利略、马略特、牛顿、笛卡尔、惠更斯等都先
后做了一些实验,总结出碰撞的规律,奠定了动量守恒的基础. 近现代通过加速器技术研究高能粒子的碰撞,产生了一种
全新的基本粒子研究手段.绝大多数粒子都是在粒子的碰撞中
发现的,当代物理离不开碰撞.2.生活中的各种碰撞现象碰撞的种类有正碰和斜碰两种. (1)正碰:像台球的碰撞中若两个小球碰
撞时的速度沿着连心线方向,则称为正碰.如
图 1-1-1 所示.图 1-1-1(2)斜碰:像台球的碰撞中若两个小球碰撞前的相对速度不在连心线上,则称为斜碰.如图 1-1-2 所示.图 1-1-23.弹性碰撞和非弹性碰撞(1)碰撞分为_________和_________撞两种. ①弹性碰撞:若两个物体的碰撞发生在水平面上,碰撞后
______________,则没有动能损失,碰撞前后两个物体构成的
系统动能相等. ②非弹性碰撞:若两个物体的碰撞发生在水平面上,碰撞
后________________或_________________,则有动能损失(或
损失最大),损失的动能转变为热能,碰撞前后两个物体构成的
系统动能不再相等,碰撞后的总动能小于碰撞前的总动能.弹性碰撞非弹性碰形变能完全恢复形变不能完全恢复完全不能恢复(黏合)(2)两种碰撞的区别:弹性碰撞没有能量损失,非弹性碰撞有能量损失. 当两个小球的碰撞发生在水平面上时,两小球碰撞前后的
重力势能不变,变化的是动能,根据动能是否守恒,把小球的
碰撞分为弹性碰撞和非弹性碰撞,如下所示:(3)注意. ①非弹性碰撞一定有机械能损失,损失的机械能一般转化
为内能.碰撞后的总机械能不可能增加,这一点尤为重要.
②系统发生爆炸时,内力对系统内的每一个物体都做正功,
故爆炸时,系统的机械能是增加的,这一增加的机械能来源于
炸药贮存的化学能.知识点 2 动量 动量守恒定律
1.动量及其变化 (1)冲量:物体受到的__与________________的乘积叫做这
个力的冲量.单位为 N·s,是一个矢量,用符号 I 表示,即 I=
Ft.冲量的方向就是力的方向. (2)动量:运动物体的____和它的____的乘积叫做这个物体
的动量.单位为 kg·m/s,是一个矢量,用符号 p 表示,即 p=
mv.动量的方向是物体运动的方向,也就是速度的方向.力这个力的作用时间质量速度(3)动量定理:合外力的冲量等于系统的动量变化量.表达式为 Ft=mvt-mv0. ①冲量的方向和动量变化量的方向是同一个方向,也是力
的方向(或是加速度的方向),冲量的方向与动量的方向不一定
相同(相同、相反,或是成某一个角度).②求某一个力的冲量有两种方法:一是用冲量的定义式 I=Ft;二是用动量定理 I=mvt- mv0.③求动量的变化量有两种方法:一是用动量变化量的定义式Δp=mvt-mv0;二是用动量定理Δp=Ft.(4)应用动量定理.
①对动量定理的理解 a.动量定理给出了状态量动量 p 和过程量冲量 I 之间的关
系,在合外力为恒力的情况下,用冲量Δp=Ft 来求物体的动量
变化量比较方便;在合外力为变力的情况下,用动量变化量的定义式Δp=mvt-mv0 来求物体的动量变化量较为方便.
b.动量定理的研究对象可以是一个物体,也可以是几个物
体组成的系统.由于系统内力的总冲量一定是零,不会改变系
统的总动量,所以对一个系统而言,“合外力的冲量等于系统
的动量变化”仍然成立. c.如果物体的运动分为几个阶段,既可以分阶段用动量定
理,也可以对全过程用动量定理.对全过程而言,把各个阶段
的冲量分别计算出来,再求其矢量和,即为物体受到的总冲量.
d.对竖直方向的打击和碰撞问题,合外力应该是撞击力和
重力的合力,不能随意忽略重力.只有在作用时间极短,撞击
力远大于重力时,重力才可以忽略不计.(5)F-t 图象中面积的物理意义. F-t 图象中的面积代表这个力的冲量.无论力是恒力还是
变力,当这个力为合外力时,F-t 图象中的面积始终代表物体
受到的冲量,等于物体的动量变化量.2.一维碰撞中的动量守恒定律 (1)系统:当两个物体相互碰撞时,这两个物体之间发生了
相互作用,把具有相互作用的这两个物体称为系统.
(2)内力和外力:________的其他物体对系统的作用力叫做外力;_________物体之间相互作用的力称为内力. (3)动量守恒定律:当一个系统所受到的__________时,系
统的_______________,这就是一维碰撞中的动量守恒定律.(4)表达式:m1v10+m2v20=m1v1+m2v2. (5)注意:动量守恒定律并不限于两个物体的相互作用,一
个系统可以包括任意数目的物体,只要整个系统受到的合外力
等于零,系统的总动量就守恒.系统外部系统内部合外力为零总动量保持不变vt-v0知识点 3 力的两大积累效应
1.力对时间的积累:I=Ft
根据牛顿第二定律:F=ma
得到 F=ma=mt,即:Ft=mvt-mv0 这就是动量定理.当合外力的__________时,很显然____
_____________,即总动量不变,这就是动量守恒定律.冲量等于零动量的变化量为零2.力对空间的积累效应:W=Fs
根据牛顿第二定律:F=mamvt-mv0【例题】人从高处跳到低处时,为了安全,一般都让脚尖先着地,这样做是为了()CA.减小冲量
B.减小动量的变化量
C.增大与地面的作用时间,从而减小冲力
D.增大人对地面的压强,起到安全作用解析:根据动量定理,F=t,脚尖先着地,增加了脚与地面的作用时间,在动量变化量一定的情况下,脚与地面
的作用力变小,起到保护作用.1.一对作用力与反作用力做的总功为 W,总冲量为 I,下列说法正确的是()A.W 一定等于零,I 不一定等于零
B.W 可能不等于零,I 一定等于零
C.W 和 I 一定都等于零
D.W 和 I 可能都不等于零 解析:一对作用力与反作用力中的两个力,既可以都做正
功(比如爆炸),也可以都做负功(比如相向运动发生碰撞而静止
的问题),也可以一个做正功,一个做负功(比如滑块在木板上
移动的问题),所以总功可能不等于零;但作用力与反作用力的
大小相等方向相反,作用时间相等,其总冲量必然等于零,只
有 B 正确.答案:B 2.(双选)从水平地面上方同一高度处,使 a 球竖直上抛,
使 b 球平抛,且两球质量相等,初速度大小相同,最后落于同一水平地面上(空气阻力不计).下列说法中正确的是()A.两球着地时的动量相同BD B.两球着地时的动能相同
C.重力对两球的冲量相同
D.重力对两球所做的功相同
解析:a、b 两球的重力相同,落下的高度相同,所以做功
相同;a、b 两球的飞行时间不同,所以重力的冲量不同.BD
正确,AC 错.知识点 4 动量守恒定律
1.动能和动量大小的换算(2)动量守恒定律成立的条件.①系统不受外力或者所受外力之和为零.②系统受外力,但外力远小于内力,可以忽略不计.
③系统在某一个方向上所受的合外力为零,则该方向上动量守恒.④全过程的某一阶段系统受的合外力为零,则该阶段系统动量守恒. 【例题】如图 1-1-3 所示的装置中,木块 B 与水平桌面
间的接触面是光滑的,子弹 A 沿水平方向射入木块后留在木块
内,将弹簧压缩到最短.现将子弹、木块和弹簧合在一起作为
研究对象(系统),则此系统在从子弹开始射入木块到弹簧压缩至最短的整个过程中( )
图 1-1-3A.动量守恒、机械能守恒B.动量不守恒、机械能不守恒
C.动量守恒、机械能不守恒
D.动量不守恒、机械能守恒 解析:若以子弹、木块和弹簧合在一起作为研究对象(系统),从
子弹开始射入木块到弹簧压缩至最短时,弹簧固定端墙壁对弹簧有外
力作用,因此动量不守恒.而在子弹射入木块时,存在剧烈摩擦作用,
有一部分能量转化为内能,机械能也不守恒.实际上,在子弹射入木
块这一瞬间过程,取子弹与木块为系统则可认为动量守恒(此瞬间弹
簧尚未形变).子弹射入木块与木块达到相同速度后压缩弹簧过程中,
机械能守恒,但动量不守恒.答案:B 3.两只小船逆向航行,航线邻近.在两船首尾相齐时,由
每只船上各自向对方放置一质量为 m=50 kg 的麻袋,结果载重
较小的船停了下来,另一船则以 v=8.5 m/s 的速度沿原方向航行.
设两只船及船上载重量分别为 m1=500 kg,m2=1 000 kg.问交
换麻袋前各船的速率是多大?(水的阻力不计) 解:每只船向对方放置麻袋过程中不会影响本船的速度,
船速之所以发生变化,是接受了对方的麻袋并与之发生相互作
用的结果.若选抛出麻袋后的此船与彼船扔来的麻袋所组成的
系统为研究对象,在水的阻力不计的情况下,系统动量守恒.
分别以各船原航行方向为正方向,则对轻船系统有(m1-m)v1-mv2=0 ①
即(500-50)v1-50v2=0对重船系统有(m2-m)v2-mv1=(m2-m+m)v ②
即(1 000-50)v2-50v1=1 000×8.5
解之可得:v1=1 m/s,v2=9 m/s.题型 1动量的矢量性与动能的标量性【例题】关于物体的动量和动能,下列说法中正确的是( )
A.一物体的动量不变,其动能一定不变
B.一物体的动能不变,其动量一定不变
C.两物体的动量相等,其动能一定相等
D.两物体的动能相等,其动量一定相等 解析:物体的动量不变实质就是速度不变,亦即速度大小
和方向均不变,所以其动能一定不变,A 对;而动能是标量,
动能不变,速度的方向是可以变化的,故其动量可以变化,B有关,又与物体的速度有关,两个物体的质量不一定相等,速
度也不一定相等,所以其动量与动能不一定相等,C、D 都错.答案:A化取决于合外力做的功,若合外力的总功不为零,动能必然变
化,若合外力的总功为零,动能必然不变;动量是矢量,表达式为 p=mv,动量是否变化取决于合外力的冲量,当合外力的冲量为零时,动量不变,当合外力的冲量不为零时,动量必然
改变.当物体的速度大小不变只是方向改变时,合外力的总功
为零,但合外力的冲量不为零,其动能是不变的,但动量的方
向必然改变. 1.(双选)一个质量为 2 kg 的物体以 2 m/s 的速度向东运动,
某时刻受到一个向西的力,过一段时间,该物体向西运动,当)其速度也为 2 m/s 时,下列说法正确的是(
A.动量变化 8 kg·m/s,向东
B.动量变化 8 kg·m/s,向西
C.动能变化为 8 J
D.动能变化为零 解析:动量是矢量,所以物体向西运动的动量 4 kg·m/s 与
向东运动时的动量 4 kg·m/s 虽然大小相同,但方向不同,所以
动量变化动量变化 8 kg·m/s,向西;动能是标量,所以未变.
BD 正确,AC 错.答案:BD题型 2动量守恒定律的简单应用 【例题】质量为 M 的小车在光滑的水平地面上以 v0 匀速运
动,当车中的沙子从底部的漏斗中不断流下时,车子速度将()BA.减小B.不变C.增大D.无法确定 解析:动量守恒的条件是合外力等于零,在沙子没有落地
之前,落下的沙子和小车组成的系统水平方向不受其他外力作
用,合外力等于零,动量守恒.在沙子没有落地之前,沙子在
水平方向和小车具有相同的速度(惯性),故小车的速度不变. 规律总结:此类问题属系统所受外力不为零,竖直方向上
受到外力,动量不守恒,但水平方向上不受外力作用,动量守
恒.又如大炮在以倾角发射炮弹时,炮身要后退,受到地面的阻
力,但因其炸药产生的作用力很大,远大于受到的阻力,故仍
认为水平方向动量守恒.在本题中,沙子未落到地面之前,沙子
的沿水平方向的速度大小不变,是解决本题的关键. 2.在光滑水平直路上停着一辆较长的木板车,车的左端站
立一个大人,车的右端站立一个小孩.如果大人向右走,小孩(质
量比大人小)向左走,他们的速度大小相同,则在他们走动过程中()BA.车可能向右运动
C.车可能保持静止B.车一定向左运动
D.无法确定 解析:系统动量守恒,他们的速度大小相同方向相反,必
有大人的动量大,故小孩和车的动量与大人的动量大小相等,
方向相反.
同课章节目录
- 第1章 动量守恒研究
- 导 入 从天体到微粒的碰撞
- 第1节 动量定理
- 第2节 动量守恒定律
- 第3节 科学探究——维弹性碰撞
- 第2章 原子结构
- 导 入 从一幅图片说起
- 第1节 电子的发现与汤姆孙模型
- 第2节 原子的核式结构模型
- 第3节 玻尔的原子模型
- 第4节 氢原子光谱与能级结构
- 专题探究 动量与原子的实验与调研
- 第3章 原子核与放射性
- 导 入 打开原子核物理的大门
- 第1节 原子核结构
- 第2节 原子核衰变及半衰期
- 第3节 放射性的应用与防护
- 第4章 核能
- 导 入 熟悉而又陌生的核能
- 第1节 核力与核能
- 第2节 核裂变
- 第3节 核聚变
- 第4节 核能的利用与环境保护
- 专题探究 原子核和核能利用的实验与调研
- 第5章 波与粒子
- 导 入 奇异的微观世界
- 第1节 光电效应
- 第2节 康普顿效应
- 第3节 实物粒子的波粒二象性
- 第4节 “基本粒子”与恒星演化
- 专题探究 波粒二象性的实验与调研
