离散型随机变量的分布列
图片预览





文档简介
课件19张PPT。2.1.2离散型随机变量的分布列教学目标:知识与技能理解取有限的离散型随机变量及其分布列的概念,掌握分布列的两个性质,并求简单的分布列,认识分布列对于刻画随机现象的重要性。过程与方法师生共同探讨、研究,从具体的实例中得到概念,会利 用分布列的性质判断一个分布列是否正确,通过师生之间,学生与学生之间互相交流,培养学生学会共同学习的能力。情感态度与价值观把生活实际问题转化为数学问题,让学生体会到数学源于生活,而高于生活的一种学科,激发学生学习数学的兴趣,以及积极性,陶冶学生的情操。一、复习回顾: 首页上页下页定义1:如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量。随机变量常用希腊字母X、Y、ξ、η表示。定义2:对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量。引例:抛掷一个骰子,设得到的点数为ξ,则ξ的取值情况如何? ξ取各个值的概率分别是什么?首页上页下页解:则 的取值有1、2、3、4、5、6列 表:二、离散型随机变量的分布列 表中从概率的角度指出了随机变量在随机试验中取值的分布状况,
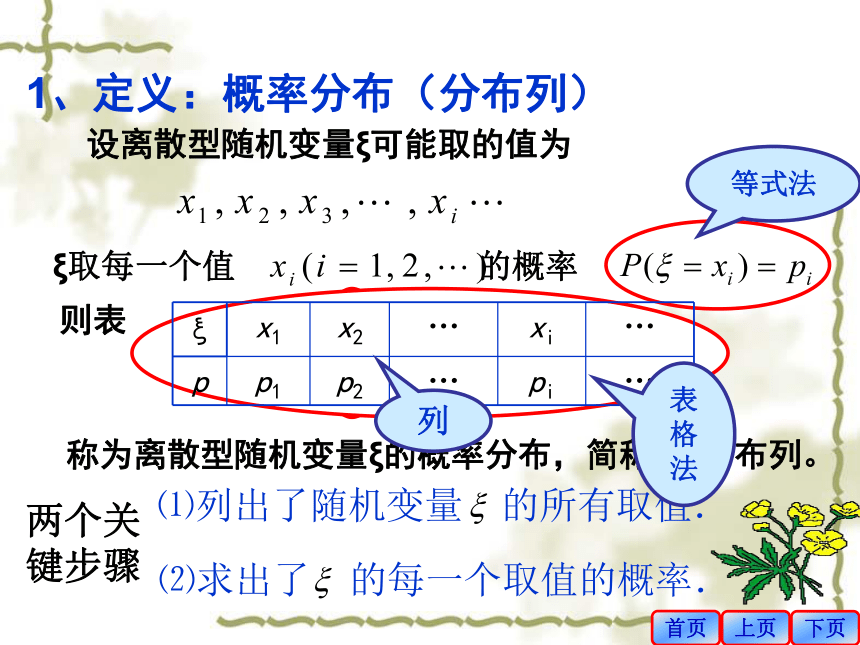
称为随机变量的概率分布列。首页下页上页称为离散型随机变量ξ的概率分布,简称ξ的分布列。则表ξ取每一个值 的概率 设离散型随机变量ξ可能取的值为1、定义:概率分布(分布列)首页下页上页两个关
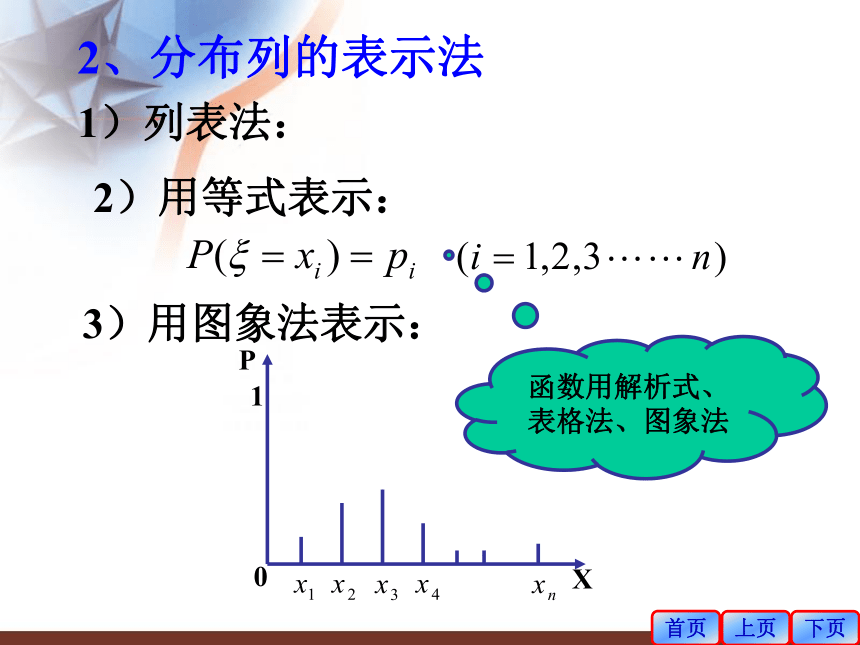
键步骤⑴列出了随机变量 的所有取值. ⑵求出了 的每一个取值的概率.等式法表格法列首页上页下页2、分布列的表示法2)用等式表示: 3)用图象法表示:PX01函数用解析式、表格法、图象法1)列表法:首页上页下页3、离散型随机变量的分布列具有下述两个性质:注:这个两个性质是判断分布列是否正确的重要依据例如:某同学求得一离散型随机变量的分布列如下:试说明该同学的计算结果是否正确? 根据射手射击所得环数ξ的分布列,有例1、某一射手射击所得环数ξ的分布列如下:求此射手” ≥7”的概率. 分析: “ ≥7”的事件有哪些? 这些事件之间有什么特点?解:P(ξ=7)=0.09,P(ξ=8)=0.28,P(ξ=9)=0.29,P(ξ=10)=0.22,所求的概率为P(ξ≥7)=0.09+ 0.28+ 0.29+ 0.22= 0.88首页上页下页三、沙场点兵 小结:一般地,离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。首页上页下页例2、随机变量ξ的分布列为1)求常数 a;解:1)由离散型随机变量的分布列的性质有:2)例3、连续抛掷两个骰子,得到的点数之和为ξ,
则ξ取哪些值?各个值对应的概率分别是什么?解:的可能取值有:2、3、4、5、6、7、8、
9、10、11、12由古典概型计算出各取值的概率得到分布列为:首页上页下页求离散型随机变量的分布列步骤:S1:求出 的所有可能取值S2:求出 取值各个值的概率 S3:列出分布列首页上页下页尝试高考: 随机抽取某厂的某种产品200件,经质检,
其中有一等品126件,二等品50件,三等品
20件,次品4件。已知生产1件一、二、
三等品获得的利润分别为6万元、2万元、
1万元,而1件次品亏损2万元。设1件产品
的利润为 (单位.万元),求 的分布列。解:的取值有:-2、1、2、6首页上页下页(2008 广东 理 17)列表:首页上页下页小结:1)、本节课学习里离散型随机变量的分 布列的概念以及求一些简单的分布列2)、分布列的性质以及应用作业:P49 练习题 第2题首页上页下页思考:(2004 辽宁 8)已知随机变量ξ的概率分布如下:求p(ξ=10)等于( )再见定义:设离散型随机变量ξ可能取的值为ξ取每一个值 的概率 则表 一盒中放有大小相同的红色、绿色、黄色三种小球,已知红球的个数是绿球个数的两倍,黄球个数是绿球个数的一半,现从该盒中随机取出一球,若取出红球得1分,取出绿 球得0分,取出黄球得-1分,试写出从该盒内随机取出一球所得分数ξ的分布列.解:设黄球的个数为n,则绿球的个数为2n,红球的个数为4n,盒中球的个数为7n,所以
P(ξ=1)= = ,P(ξ=0)= = ,
P(ξ=-1)= = . 所以从该盒中随机取出一球
所得分数ξ的分布列为:
称为随机变量的概率分布列。首页下页上页称为离散型随机变量ξ的概率分布,简称ξ的分布列。则表ξ取每一个值 的概率 设离散型随机变量ξ可能取的值为1、定义:概率分布(分布列)首页下页上页两个关
键步骤⑴列出了随机变量 的所有取值. ⑵求出了 的每一个取值的概率.等式法表格法列首页上页下页2、分布列的表示法2)用等式表示: 3)用图象法表示:PX01函数用解析式、表格法、图象法1)列表法:首页上页下页3、离散型随机变量的分布列具有下述两个性质:注:这个两个性质是判断分布列是否正确的重要依据例如:某同学求得一离散型随机变量的分布列如下:试说明该同学的计算结果是否正确? 根据射手射击所得环数ξ的分布列,有例1、某一射手射击所得环数ξ的分布列如下:求此射手” ≥7”的概率. 分析: “ ≥7”的事件有哪些? 这些事件之间有什么特点?解:P(ξ=7)=0.09,P(ξ=8)=0.28,P(ξ=9)=0.29,P(ξ=10)=0.22,所求的概率为P(ξ≥7)=0.09+ 0.28+ 0.29+ 0.22= 0.88首页上页下页三、沙场点兵 小结:一般地,离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。首页上页下页例2、随机变量ξ的分布列为1)求常数 a;解:1)由离散型随机变量的分布列的性质有:2)例3、连续抛掷两个骰子,得到的点数之和为ξ,
则ξ取哪些值?各个值对应的概率分别是什么?解:的可能取值有:2、3、4、5、6、7、8、
9、10、11、12由古典概型计算出各取值的概率得到分布列为:首页上页下页求离散型随机变量的分布列步骤:S1:求出 的所有可能取值S2:求出 取值各个值的概率 S3:列出分布列首页上页下页尝试高考: 随机抽取某厂的某种产品200件,经质检,
其中有一等品126件,二等品50件,三等品
20件,次品4件。已知生产1件一、二、
三等品获得的利润分别为6万元、2万元、
1万元,而1件次品亏损2万元。设1件产品
的利润为 (单位.万元),求 的分布列。解:的取值有:-2、1、2、6首页上页下页(2008 广东 理 17)列表:首页上页下页小结:1)、本节课学习里离散型随机变量的分 布列的概念以及求一些简单的分布列2)、分布列的性质以及应用作业:P49 练习题 第2题首页上页下页思考:(2004 辽宁 8)已知随机变量ξ的概率分布如下:求p(ξ=10)等于( )再见定义:设离散型随机变量ξ可能取的值为ξ取每一个值 的概率 则表 一盒中放有大小相同的红色、绿色、黄色三种小球,已知红球的个数是绿球个数的两倍,黄球个数是绿球个数的一半,现从该盒中随机取出一球,若取出红球得1分,取出绿 球得0分,取出黄球得-1分,试写出从该盒内随机取出一球所得分数ξ的分布列.解:设黄球的个数为n,则绿球的个数为2n,红球的个数为4n,盒中球的个数为7n,所以
P(ξ=1)= = ,P(ξ=0)= = ,
P(ξ=-1)= = . 所以从该盒中随机取出一球
所得分数ξ的分布列为:
