广东中山大学附属中学三水实验学校八年级数学下册北师大版课件:1.2.1直角三角形 (共27张PPT)
文档属性
| 名称 | 广东中山大学附属中学三水实验学校八年级数学下册北师大版课件:1.2.1直角三角形 (共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 438.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-26 09:28:14 | ||
图片预览






文档简介
课件27张PPT。第一章 三角形的证明 1.2.1 直角三角形
学习目标1.经历探索、猜测、证明的过程,了解勾股定理及其逆定理的证明方法,发展学生初步的演绎推理能力。
2.结合具体例子了解逆命题、逆定理的概念,会识别两个互逆命题、互逆定理,知道原命题成立其逆命题不一定成立。 复习提问:
1、直角三角形的角有哪些性质? 一般性质:
直角三角形的角具有一般三角形的所有性质.特殊性质:直角三角形两锐角互余.2、直角三角形的边有哪些性质? 一般性质:直角三角形的边具有一般三角
形的所有性质. 特殊性质:在直角三角形中,如果一个锐
角等于30,那么它所对的直角
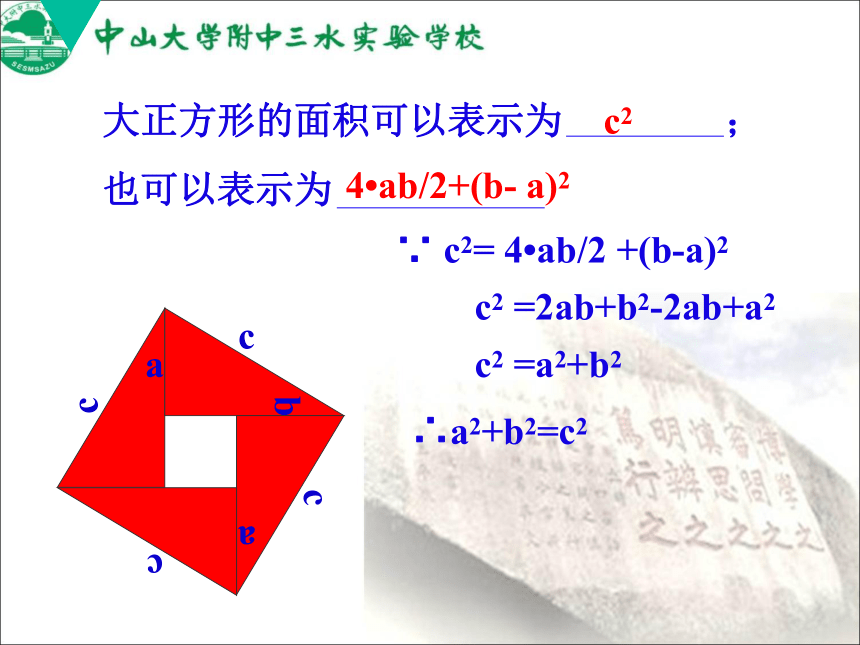
边等于斜边的一半. 勾股定理:如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.勾股定理在西方文献中又称为毕达哥拉斯定理∵ (a+b)2 = c2 + 4?ab/2a2+2ab+b2 = c2 +2ab∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为(a+b)2c2 +4?ab/2∵ c2= 4?ab/2 +(b-a)2 c2 =2ab+b2-2ab+a2 c2 =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为c24?ab/2+(b- a)2
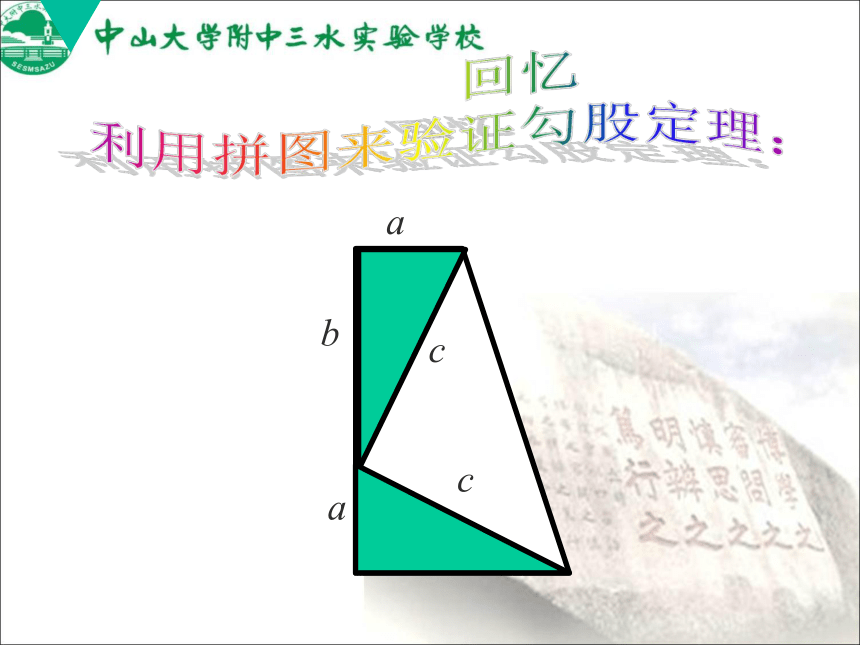
回忆
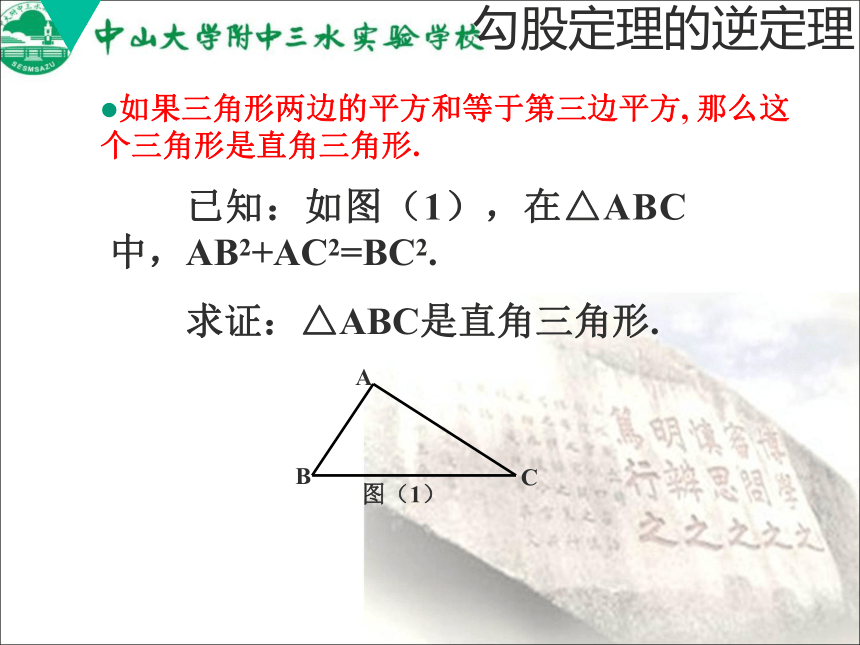
利用拼图来验证勾股定理:美国第十七任总统的证法 已知:如图(1),在△ABC中,AB2+AC2=BC2.
求证:△ABC是直角三角形.勾股定理的逆定理如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.证明:作Rt△A′B′C′,使∠A′=90°,A′B′=AB,A′C′=AC(如图(2)),则A′B′2+A′C′2=B′C′2(勾股定理). ∵AB2+AC2=BC2 , A′B′=AB,A′C′=AC, ∴BC2=B′C′2. ∴BC=B′C′. ∴△ABC≌△A′B′C′(SSS). ∴∠A==∠A′=90°(全等三角形的对应角相等).
因此,△ABC是直角三角形. 几何的三种语言′驶向胜利的彼岸勾股定理的逆定理
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.这是判定直角三角形的根据之一.在△ABC中
∵AC2+BC2=AB2(已知),
∴△ABC是直角三角形(如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形).及时练:
1、一个三角形的三边之比为 ∶ ∶ ,
这个三角形的形状是( )
2、已知:线段a∶b∶c的值如下,则能够组成直角三角形的是( )
(A)3∶4∶6 (B)5∶12∶13
(C)1∶2∶4 (4)1∶3∶5
1.在△ABC中,已知,AB=13cm,BC=10cm,BC边上的中线AD=12cm ,
求证:AB=AC 定理: 直角三角形两条直角边的平方
和等于斜边的平方。 命题: 如果一个三角形两边的平方和等于第三边的平方,那么这个三形是直角三角形。 两个命题的条件和结论有什么
样的关系?在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?它们都是真命题吗? 逆命题:如果两个有理数的平方相等,那么这两个有理数相等.
原命题是真命题,逆命题是假命题.
巩固练习:
说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果ab=0,那么a=0,b=0.
提问:一个命题是真命题,它的逆命题一定是真命题吗?
定理与逆定理一个命题是真命题,它逆命题却不一定是真命题.你还能举出一些例子吗?想一想:互逆命题与互逆定理有何关系?如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理. 互逆定理:如果一个定理的逆命题经过证明是真命题,那么它也是个定理,这两个定理称为互逆定理,其中一个定理称为另一个定理的逆定理. 判断正误:
(1)互逆命题一定是互逆定理;
(2)互逆定理一定是互逆命题.
我们已经学习了一些互逆定理,如勾股定理及其逆定理、“两直线平行,内错角相等与“内错角相等,两直线平行”等.请你再举出一些互逆定理的例子.
巩固练习:
1、写出下列命题的逆命题,并判断每对命题的真假:
(2)矩形是正方形;
(3)如果x2﹥0,那么x﹥0;(4)直角都相等.2、在△ABC中,已知AB=13cm,BC=10cm,BC边上的中线AD=12cm.求证:AB=AC.
已知:△ABC中,∠ C=600,AB=14,AC=10,AD是BC边上的高,求BC的长解后反思:
在直角三角形中,利用勾股定理计算线段的长,是勾股定理的一个重要应用,在有直角三角形时,可直接应用,在没有直角三角形时,常作垂线构造直角三角形,为能应用勾股定理创造条件。习题1.4 3.如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲从正四棱柱的底面上的点A沿棱柱侧面到点C1处吃食物,那么它需要爬行的最短路径是多少? 提示:对于空间图形需要动手操作,将其转化为平面图形来解决. 已知:在△ABC中, ∠ C=900, AD是BC边上的中线,DE⊥AB,垂足为E,
求证:AC2=AE2-BE2解后反思证明线段的平方和或差,常常考虑运用勾股定理,若无直角三角形,可通过作垂线构造直角三角形,以便运用勾股定理。梦想成真1.如图(单位:英尺),在一个长方体的房间里,一只蜘蛛在一面墙的正中间离天花板1英尺的A处,苍蝇则在对面墙的正中间离地板1英尺的B处.
试问:蜘蛛为了捕获苍蝇,需要爬行的最短距离是多少?提高练习: 1、如图,在四边形ABCD中,AB=2,BC= CD=5,DA=4,∠B=90°求四边形ABCD的面积. 2、在△ABC中,若∠A∶∠B∶∠C=1∶2∶3,则BC∶AC∶AB = ?则△ABC是 三角形.课堂小结当堂检测:
《学案》P10课时达标
学习目标1.经历探索、猜测、证明的过程,了解勾股定理及其逆定理的证明方法,发展学生初步的演绎推理能力。
2.结合具体例子了解逆命题、逆定理的概念,会识别两个互逆命题、互逆定理,知道原命题成立其逆命题不一定成立。 复习提问:
1、直角三角形的角有哪些性质? 一般性质:
直角三角形的角具有一般三角形的所有性质.特殊性质:直角三角形两锐角互余.2、直角三角形的边有哪些性质? 一般性质:直角三角形的边具有一般三角
形的所有性质. 特殊性质:在直角三角形中,如果一个锐
角等于30,那么它所对的直角
边等于斜边的一半. 勾股定理:如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.勾股定理在西方文献中又称为毕达哥拉斯定理∵ (a+b)2 = c2 + 4?ab/2a2+2ab+b2 = c2 +2ab∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为(a+b)2c2 +4?ab/2∵ c2= 4?ab/2 +(b-a)2 c2 =2ab+b2-2ab+a2 c2 =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为c24?ab/2+(b- a)2
回忆
利用拼图来验证勾股定理:美国第十七任总统的证法 已知:如图(1),在△ABC中,AB2+AC2=BC2.
求证:△ABC是直角三角形.勾股定理的逆定理如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.证明:作Rt△A′B′C′,使∠A′=90°,A′B′=AB,A′C′=AC(如图(2)),则A′B′2+A′C′2=B′C′2(勾股定理). ∵AB2+AC2=BC2 , A′B′=AB,A′C′=AC, ∴BC2=B′C′2. ∴BC=B′C′. ∴△ABC≌△A′B′C′(SSS). ∴∠A==∠A′=90°(全等三角形的对应角相等).
因此,△ABC是直角三角形. 几何的三种语言′驶向胜利的彼岸勾股定理的逆定理
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.这是判定直角三角形的根据之一.在△ABC中
∵AC2+BC2=AB2(已知),
∴△ABC是直角三角形(如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形).及时练:
1、一个三角形的三边之比为 ∶ ∶ ,
这个三角形的形状是( )
2、已知:线段a∶b∶c的值如下,则能够组成直角三角形的是( )
(A)3∶4∶6 (B)5∶12∶13
(C)1∶2∶4 (4)1∶3∶5
1.在△ABC中,已知,AB=13cm,BC=10cm,BC边上的中线AD=12cm ,
求证:AB=AC 定理: 直角三角形两条直角边的平方
和等于斜边的平方。 命题: 如果一个三角形两边的平方和等于第三边的平方,那么这个三形是直角三角形。 两个命题的条件和结论有什么
样的关系?在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?它们都是真命题吗? 逆命题:如果两个有理数的平方相等,那么这两个有理数相等.
原命题是真命题,逆命题是假命题.
巩固练习:
说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果ab=0,那么a=0,b=0.
提问:一个命题是真命题,它的逆命题一定是真命题吗?
定理与逆定理一个命题是真命题,它逆命题却不一定是真命题.你还能举出一些例子吗?想一想:互逆命题与互逆定理有何关系?如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理. 互逆定理:如果一个定理的逆命题经过证明是真命题,那么它也是个定理,这两个定理称为互逆定理,其中一个定理称为另一个定理的逆定理. 判断正误:
(1)互逆命题一定是互逆定理;
(2)互逆定理一定是互逆命题.
我们已经学习了一些互逆定理,如勾股定理及其逆定理、“两直线平行,内错角相等与“内错角相等,两直线平行”等.请你再举出一些互逆定理的例子.
巩固练习:
1、写出下列命题的逆命题,并判断每对命题的真假:
(2)矩形是正方形;
(3)如果x2﹥0,那么x﹥0;(4)直角都相等.2、在△ABC中,已知AB=13cm,BC=10cm,BC边上的中线AD=12cm.求证:AB=AC.
已知:△ABC中,∠ C=600,AB=14,AC=10,AD是BC边上的高,求BC的长解后反思:
在直角三角形中,利用勾股定理计算线段的长,是勾股定理的一个重要应用,在有直角三角形时,可直接应用,在没有直角三角形时,常作垂线构造直角三角形,为能应用勾股定理创造条件。习题1.4 3.如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲从正四棱柱的底面上的点A沿棱柱侧面到点C1处吃食物,那么它需要爬行的最短路径是多少? 提示:对于空间图形需要动手操作,将其转化为平面图形来解决. 已知:在△ABC中, ∠ C=900, AD是BC边上的中线,DE⊥AB,垂足为E,
求证:AC2=AE2-BE2解后反思证明线段的平方和或差,常常考虑运用勾股定理,若无直角三角形,可通过作垂线构造直角三角形,以便运用勾股定理。梦想成真1.如图(单位:英尺),在一个长方体的房间里,一只蜘蛛在一面墙的正中间离天花板1英尺的A处,苍蝇则在对面墙的正中间离地板1英尺的B处.
试问:蜘蛛为了捕获苍蝇,需要爬行的最短距离是多少?提高练习: 1、如图,在四边形ABCD中,AB=2,BC= CD=5,DA=4,∠B=90°求四边形ABCD的面积. 2、在△ABC中,若∠A∶∠B∶∠C=1∶2∶3,则BC∶AC∶AB = ?则△ABC是 三角形.课堂小结当堂检测:
《学案》P10课时达标
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
