广东中山大学附属中学三水实验学校七年级数学下册北师大版课件:2.3.2 平行线性质 (共15张PPT)
文档属性
| 名称 | 广东中山大学附属中学三水实验学校七年级数学下册北师大版课件:2.3.2 平行线性质 (共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 153.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-26 10:11:24 | ||
图片预览





文档简介
课件15张PPT。3.2、平行线性质邹道坚第二章 平行线和相交线1: 平行线的性质有哪几条?
2:判定两条直线平行的定理有哪几个?课前提问:(2分钟)学习目标
1.掌握平行线的判定与平行线的性质的区别,
2.灵活地综合利用平行线的判定和性质解决实际问题。自学课本P52页至例2,尝试解决以下问题:1.通过例1,归纳判断两直线平行的依据.2.在例2中学习平行线的传递性. 学生自学,教师巡视(4分钟)即平行于同一条直线的两条直线互相平行自学指导11:如图,选择合适的内容填空。
(1)∵AB//CD
∴∠1=∠2( )
(2)∵∠3=∠1
∴ //__ (同位角相等,两直线平行)
(3)∵∠1+∠ =180? ,
∴ AB//CD( ) 两直线平行,内错角相等同旁内角互补,两直线平行ABCD42:∵AB//CDEF//CD∴ //
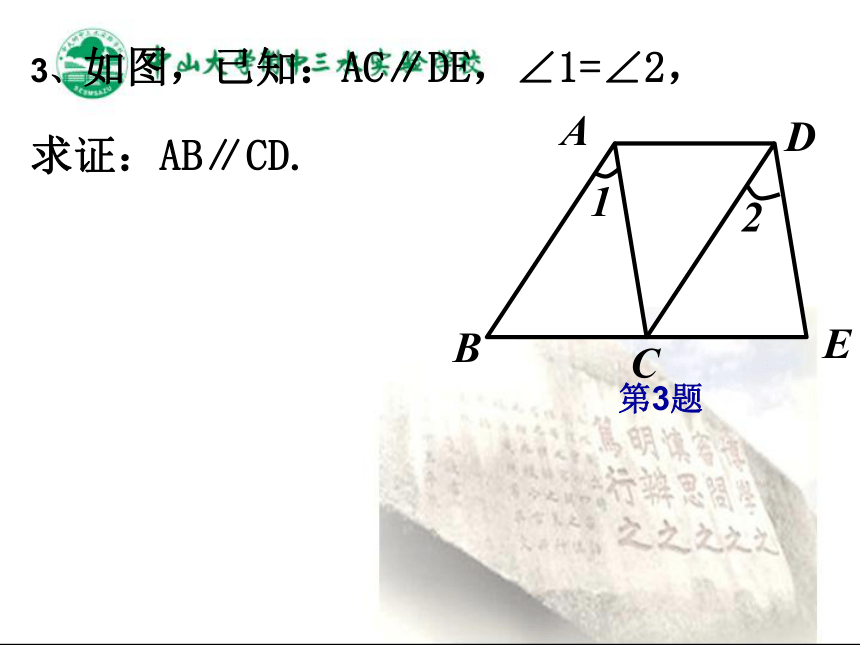
( )ABEF平行于同一条直线的两条直线互相平行自学检测1(8分钟)3、如图,已知:AC∥DE,∠1=∠2,
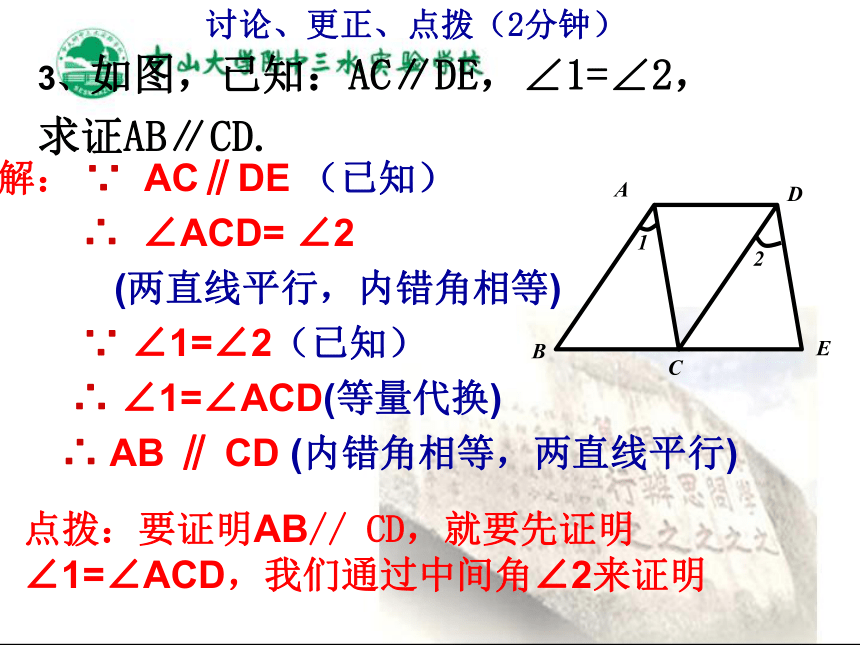
求证:AB∥CD. 2C 解: ∵ AC∥DE (已知)
∴ ∠ACD= ∠2
(两直线平行,内错角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠ACD(等量代换)
∴ AB ∥ CD (内错角相等,两直线平行)3、如图,已知:AC∥DE,∠1=∠2,求证AB∥CD. 点拨:要证明AB// CD,就要先证明∠1=∠ACD,我们通过中间角∠2来证明讨论、更正、点拨(2分钟)自学课本P52页例3至P53想一想的内容:1.理解在例3中的说理过程.
2.两条直线被第三条直线所截,如果同位角相等,那么内错角相等吗?同旁内角互补吗?学生自学,教师巡视(3分钟)自学指导2 如图,AE∥BC, AE平分∠DAC ,求证:∠B=∠C证明∵ AE∥BC(已知)∴?1= ?B(两直线平行,同位角相等)∴∠B=∠C(等量代换)∵ AE平分∠DAC (已知)∴∠1=?2(角平分线定理)?2= ?C (两直线平行,内错角相等)点拨:我们通常用等量代换得到一些较相等自学检测2(6分钟)小结(2分钟):同位角相等
内错角相等同旁内角互补同位角相等
内错角相等同旁内角互补注意判定和性质二者之间的区别2.已知∠DAC= ∠ACB, ∠D+∠DFE
=1800,试说明:EF//BC第4题图第2题图当堂训练(15分钟)1.如,一个宽度相等的纸条,折叠一下,那么∠ 1=__65°3、如图,AB ∥ CD,EG,FH分别 是∠ CEK, ∠ EFA的角平分线,则 EG∥HF. 请说明理由.4、 (选做)如图4,已知AB∥CD,∠ABF=∠DCE.试说明:∠BFE=∠FEC. 第3题图2、已知∠DAC= ∠ACB, ∠D+∠DFE=1800,求证:EF//BC 证明:
∵ ∠DAC= ∠ACB (已知)
∴AD// BC (内错角相等,两直线平行)
∵ ∠D+∠DFE=1800(已知)
∴ AD// EF (同旁内角互补,两直线平行)
∴ EF// BC(平行于同一条直线的两条直线互相平行)3.如图,AB ∥ CD,EG,FH 分别是 ∠ CEK, ∠ EFA 的角平分线, 则 EG∥HF. 请说明理由. 解 ∵ AB ∥ CD
∴ ∠KEC=∠EFA ( 两直线平行,同位角相等)
∵EG,FH分别是∠CEK, ∠ EFA的角平分线,
∴ ∠KEG= ∠KEC, ∠EFH= ∠EFA
∴ ∠KEG=∠EFH
∴EG∥HF(同位角相等,两直线平行)
4、如图7,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC. (选做题)图7证明:连接BC,
∵ AB∥CD (已知)
∴ ∠ABC=∠BCD (两直线平行,内错角相等)
∵ ∠ABF=∠DCE (已知)
∴ ∠FBC=∠BCE
∴ FB∥CE (内错角相等,两直线平行)
∴ ∠BFE=∠FEC(两直线平行,内错角相等)
同位角相等
内错角相等同旁内角互补同位角相等
内错角相等同旁内角互补注意判定和性质二者之间的区别当堂检测
2:判定两条直线平行的定理有哪几个?课前提问:(2分钟)学习目标
1.掌握平行线的判定与平行线的性质的区别,
2.灵活地综合利用平行线的判定和性质解决实际问题。自学课本P52页至例2,尝试解决以下问题:1.通过例1,归纳判断两直线平行的依据.2.在例2中学习平行线的传递性. 学生自学,教师巡视(4分钟)即平行于同一条直线的两条直线互相平行自学指导11:如图,选择合适的内容填空。
(1)∵AB//CD
∴∠1=∠2( )
(2)∵∠3=∠1
∴ //__ (同位角相等,两直线平行)
(3)∵∠1+∠ =180? ,
∴ AB//CD( ) 两直线平行,内错角相等同旁内角互补,两直线平行ABCD42:∵AB//CDEF//CD∴ //
( )ABEF平行于同一条直线的两条直线互相平行自学检测1(8分钟)3、如图,已知:AC∥DE,∠1=∠2,
求证:AB∥CD. 2C 解: ∵ AC∥DE (已知)
∴ ∠ACD= ∠2
(两直线平行,内错角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠ACD(等量代换)
∴ AB ∥ CD (内错角相等,两直线平行)3、如图,已知:AC∥DE,∠1=∠2,求证AB∥CD. 点拨:要证明AB// CD,就要先证明∠1=∠ACD,我们通过中间角∠2来证明讨论、更正、点拨(2分钟)自学课本P52页例3至P53想一想的内容:1.理解在例3中的说理过程.
2.两条直线被第三条直线所截,如果同位角相等,那么内错角相等吗?同旁内角互补吗?学生自学,教师巡视(3分钟)自学指导2 如图,AE∥BC, AE平分∠DAC ,求证:∠B=∠C证明∵ AE∥BC(已知)∴?1= ?B(两直线平行,同位角相等)∴∠B=∠C(等量代换)∵ AE平分∠DAC (已知)∴∠1=?2(角平分线定理)?2= ?C (两直线平行,内错角相等)点拨:我们通常用等量代换得到一些较相等自学检测2(6分钟)小结(2分钟):同位角相等
内错角相等同旁内角互补同位角相等
内错角相等同旁内角互补注意判定和性质二者之间的区别2.已知∠DAC= ∠ACB, ∠D+∠DFE
=1800,试说明:EF//BC第4题图第2题图当堂训练(15分钟)1.如,一个宽度相等的纸条,折叠一下,那么∠ 1=__65°3、如图,AB ∥ CD,EG,FH分别 是∠ CEK, ∠ EFA的角平分线,则 EG∥HF. 请说明理由.4、 (选做)如图4,已知AB∥CD,∠ABF=∠DCE.试说明:∠BFE=∠FEC. 第3题图2、已知∠DAC= ∠ACB, ∠D+∠DFE=1800,求证:EF//BC 证明:
∵ ∠DAC= ∠ACB (已知)
∴AD// BC (内错角相等,两直线平行)
∵ ∠D+∠DFE=1800(已知)
∴ AD// EF (同旁内角互补,两直线平行)
∴ EF// BC(平行于同一条直线的两条直线互相平行)3.如图,AB ∥ CD,EG,FH 分别是 ∠ CEK, ∠ EFA 的角平分线, 则 EG∥HF. 请说明理由. 解 ∵ AB ∥ CD
∴ ∠KEC=∠EFA ( 两直线平行,同位角相等)
∵EG,FH分别是∠CEK, ∠ EFA的角平分线,
∴ ∠KEG= ∠KEC, ∠EFH= ∠EFA
∴ ∠KEG=∠EFH
∴EG∥HF(同位角相等,两直线平行)
4、如图7,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC. (选做题)图7证明:连接BC,
∵ AB∥CD (已知)
∴ ∠ABC=∠BCD (两直线平行,内错角相等)
∵ ∠ABF=∠DCE (已知)
∴ ∠FBC=∠BCE
∴ FB∥CE (内错角相等,两直线平行)
∴ ∠BFE=∠FEC(两直线平行,内错角相等)
同位角相等
内错角相等同旁内角互补同位角相等
内错角相等同旁内角互补注意判定和性质二者之间的区别当堂检测
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
