1.1 等腰三角形的判定 同步练习(无答案)
文档属性
| 名称 | 1.1 等腰三角形的判定 同步练习(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 26.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-26 21:33:41 | ||
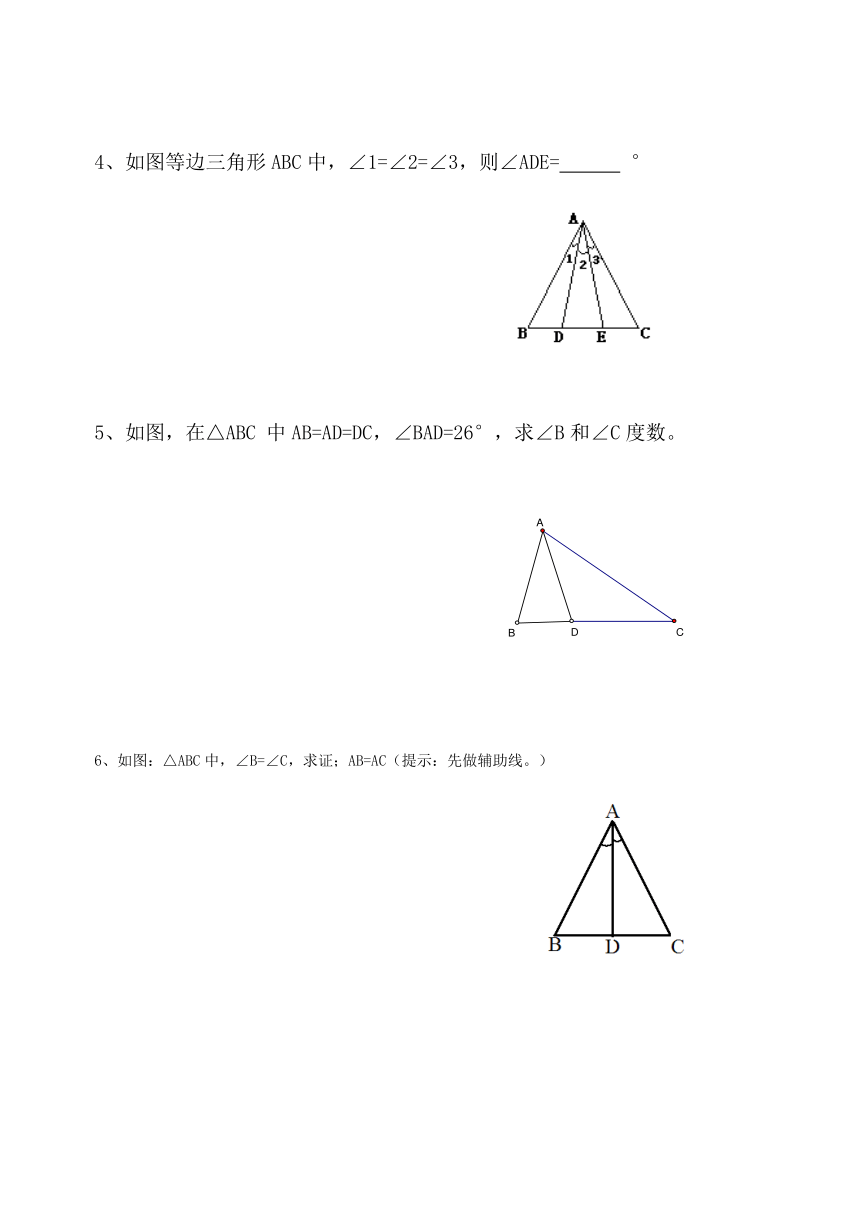
图片预览

文档简介
等腰三角形的判定
同步练习
等腰三角形的性质有:
①性质1:等腰三角形的两底角
(简单叙述为:
)
∵
∴
②性质2:等腰三角形的
互相重合
∵
∴
∵
∴
∵
∴
等边三角形的性质:
等边三角形的三个角都是
,并且每个角都等于
。
1、等腰三角形有两条边长为4cm和9cm,则该三角形的周长是(
)
A.17cm
B.22cm
C.17cm或22cm
D.18cm
2、等腰三角形的顶角是80°,则一腰上的高与底边的夹角是(
)
A.40°
B.50°
C.60°
D.30°
3、已知一个等边三角形周长为12cm,则它的面积是
cm。
4、如图等边三角形ABC中,∠1=∠2=∠3,则∠ADE=
°
5、如图,在△ABC
中AB=AD=DC,∠BAD=26°,求∠B和∠C度数。
6、如图:△ABC中,∠B=∠C,求证;AB=AC(提示:先做辅助线。)
八年级数学
1.1.3等腰三角形的判定
等腰三角形判定定理:
(简单叙述为:
)
∵
∴
例2:已知,如图,AB=DC,BD=CA,BD与CA相交于点E。
求证:△AED是等腰三角形。
情境导入
小龙和小明看过电影后走出电影院,小明扫视周围后不假思索的唠叨:“下了雨,天还这么热。”
小明很诧异,问:“哪里下了雨?”“你没看到马路快车道上全是湿漉漉的吗?”
“没有下雨,这是洒水车洒的。”
小明有理有据的回答:“如果下雨的话,不仅快车道上湿,慢车道和人行道上也要湿。你看,除了快车道外,其它地方都不湿,所以肯定刚才没下雨,”
小龙点点头笑道:“不错,是没有下雨,怪不得天这么闷热。”
思考讨论:
小龙为什么会赞同小明的分析?小明在分析的过程中体现了一种什么数学方法呢?
反证法:先假设命题的结论不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立。
例3:用反证法证明:一个三角形中不能有两个角是直角。
已知:△ABC。
求证:∠A,∠B,∠C中不能有两个角是直角。
课后反思:这节课你学会了什么?
同步练习
等腰三角形的性质有:
①性质1:等腰三角形的两底角
(简单叙述为:
)
∵
∴
②性质2:等腰三角形的
互相重合
∵
∴
∵
∴
∵
∴
等边三角形的性质:
等边三角形的三个角都是
,并且每个角都等于
。
1、等腰三角形有两条边长为4cm和9cm,则该三角形的周长是(
)
A.17cm
B.22cm
C.17cm或22cm
D.18cm
2、等腰三角形的顶角是80°,则一腰上的高与底边的夹角是(
)
A.40°
B.50°
C.60°
D.30°
3、已知一个等边三角形周长为12cm,则它的面积是
cm。
4、如图等边三角形ABC中,∠1=∠2=∠3,则∠ADE=
°
5、如图,在△ABC
中AB=AD=DC,∠BAD=26°,求∠B和∠C度数。
6、如图:△ABC中,∠B=∠C,求证;AB=AC(提示:先做辅助线。)
八年级数学
1.1.3等腰三角形的判定
等腰三角形判定定理:
(简单叙述为:
)
∵
∴
例2:已知,如图,AB=DC,BD=CA,BD与CA相交于点E。
求证:△AED是等腰三角形。
情境导入
小龙和小明看过电影后走出电影院,小明扫视周围后不假思索的唠叨:“下了雨,天还这么热。”
小明很诧异,问:“哪里下了雨?”“你没看到马路快车道上全是湿漉漉的吗?”
“没有下雨,这是洒水车洒的。”
小明有理有据的回答:“如果下雨的话,不仅快车道上湿,慢车道和人行道上也要湿。你看,除了快车道外,其它地方都不湿,所以肯定刚才没下雨,”
小龙点点头笑道:“不错,是没有下雨,怪不得天这么闷热。”
思考讨论:
小龙为什么会赞同小明的分析?小明在分析的过程中体现了一种什么数学方法呢?
反证法:先假设命题的结论不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立。
例3:用反证法证明:一个三角形中不能有两个角是直角。
已知:△ABC。
求证:∠A,∠B,∠C中不能有两个角是直角。
课后反思:这节课你学会了什么?
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
