探索三角形全等的条件同步练习(含答案)
文档属性
| 名称 | 探索三角形全等的条件同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 167.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-26 21:50:17 | ||
图片预览


文档简介
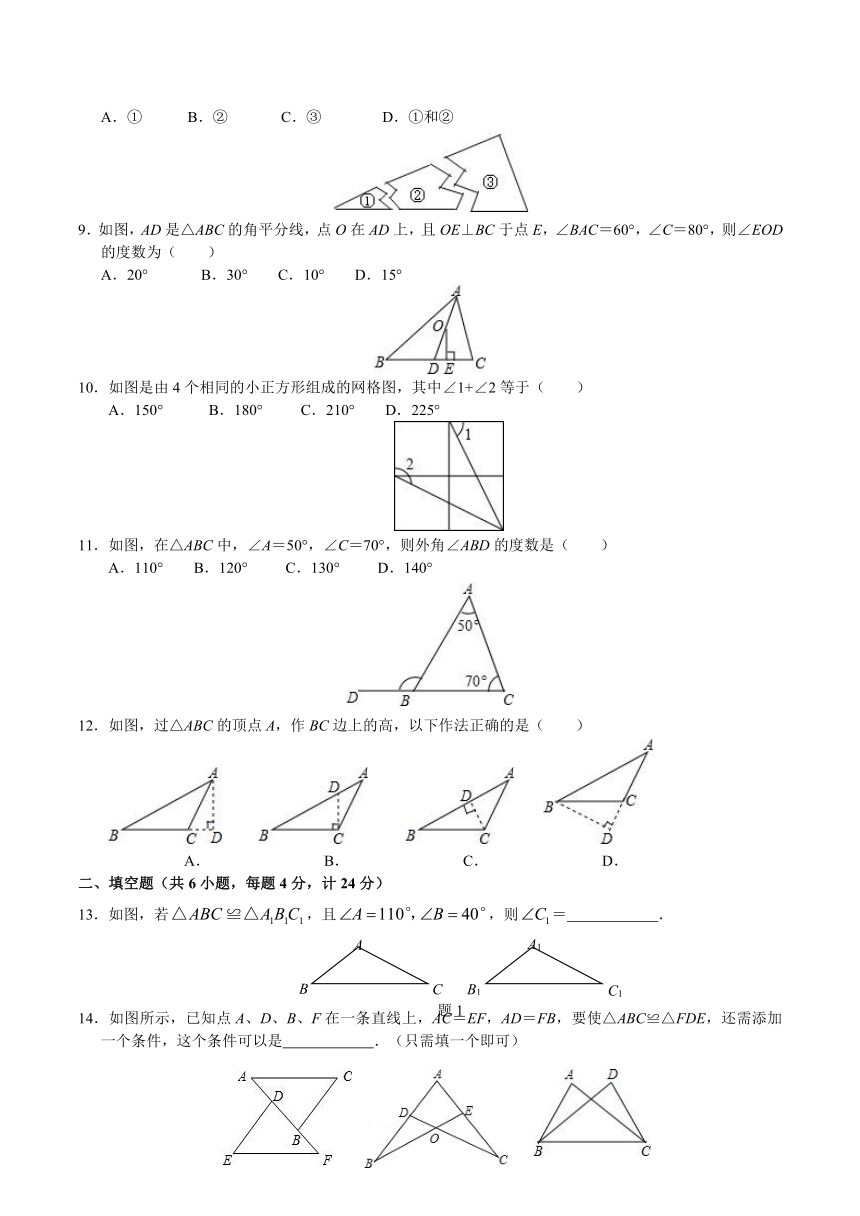
第四章
三角形(7~10课时)
同步练习
一、选择题(共12小题,每题4分,计48分)
1.如图,若
△ABC≌△DEF,∠E等于(
)
A.30°
B.50°
C.60°
D.100°
第1题图
第2题图
2.如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是(
)
A.∠BCA=∠F
B.∠B=∠E
C.BC∥EF
D.∠A=∠EDF
3.如图,CB=CD,∠B=∠D=90°,∠BAC=35°,则∠BCD的度数为(
)
A.145°
B.130°
C.110°
D.70°
第3题图
第4题图
4.如图,已知
AB=CD,AE⊥
BD于
E,CF⊥
BD于
F,AE=CF,则图中全等三角形有(
)
A.1对
B.2对
C.3对
D.4对
5.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是(
)
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
第5题图
第6题图
6.如图,已知AE=CF,∠AFD=∠CEB,那么添加一个条件后,仍无法判定△ADF≌△CBE的是(
)
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
7.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A.两点之间的线段最短
B.长方形的四个角都是直角
C.长方形是轴对称图形
D.三角形有稳定性
8.小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )
A.①
B.②
C.③
D.①和②
9.如图,AD是△ABC的角平分线,点O在AD上,且OE⊥BC于点E,∠BAC=60°,∠C=80°,则∠EOD的度数为( )
A.20°
B.30°
C.10°
D.15°
10.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.150°
B.180°
C.210°
D.225°
11.如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是( )
A.110°
B.120°
C.130°
D.140°
12.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A.
B.
C.
D.
二、填空题(共6小题,每题4分,计24分)
13.如图,若,且,则=
.
14.如图所示,已知点A、D、B、F在一条直线上,AC=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是
.(只需填一个即可)
第14题
第15题
第16题
15.如图,点D,E分别在线段AB,AC上,BE,CD相交于点O,AE=AD,要使△ABE≌△ACD,需添加一个条件是
(只需一个即可,图中不能再添加其他点或线).
16.如图,己知AC=BD,要使△ABC≌△DCB,则只需添加一个适当的条件是
(填一个即可)
17.如图,点B在线段AE上,∠1=∠2,如果添加一个条件,即可得到△ABC≌△ABD,那么这个条件可以是
___________________(要求:不在图中添加其他辅助线,写出一个条件即可)
18.已知三角形的两边长分别为3和6,那么第三边长x的取值范围是
___________________.
三、解答题(共6小题,每题7分,共28分,)
19.如图,点A、B、C、D在同一条直线上,BE∥DF,∠A=∠F,AB=FD.
求证:AE=FC.
20.如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.
求证:△ABC≌△DEF.
21.如图,点E、F在AC上,AB∥CD,AB=CD,AE=CF.求证:△ABF≌△CDE.
22.如图,点A.B.D.E在同一直线上,AD=EB,BC∥DF,∠C=∠F.
求证:AC=EF.
答
案
部
分
一、选择题
1.D
2.B
3.C
4.C
5.
B
6.B
7.D
8.C
9.A
10.B
11.B
12.A
二、填空题
13.30°
14.BC=DE或∠A=∠F或AC∥EF
15.AB=AC或∠B=∠C或∠AEB=∠ADC
16.AB=DC或∠ACB=∠DBC
17.AC=AD或∠C=∠D或∠ABC=∠ABD或∠CBE=∠DBE
18.3<x<9
三、解答题:
19.证明:∵BE∥DF,
∴∠EBA=∠D.
在△ABE和△FDC中
∵
∴△ABE≌△FDC(ASA).
∴AE=FC.
20.证明:∵BE=CF,
∴BE+CE=CF+CE.
∴BC=EF.
∵AB∥DE,
∴∠B=∠DEF.
在△ABC和△DEF中
∵
∴△ABC≌△DEF(ASA).
21.证明:∵AB∥CD,
∴∠A=∠C.
∵AE=FC,
∴AE+EF=CF+EF.
∴AF=CE.
在△ABF和△CDE中
∵
∴△ABF≌△CDE(SAS)
22.证明:∵AD=EB,
∴AD―BD=BE―BD.
∴AB=DE.
∵BC∥DF,
∴∠CBD=∠EDF.
∴∠ABC=∠EDF
在△ABC和△EDF中
∵
∴△ABC≌△EDF(AAS)
A
B
C
C1
A1
B1
题1
三角形(7~10课时)
同步练习
一、选择题(共12小题,每题4分,计48分)
1.如图,若
△ABC≌△DEF,∠E等于(
)
A.30°
B.50°
C.60°
D.100°
第1题图
第2题图
2.如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是(
)
A.∠BCA=∠F
B.∠B=∠E
C.BC∥EF
D.∠A=∠EDF
3.如图,CB=CD,∠B=∠D=90°,∠BAC=35°,则∠BCD的度数为(
)
A.145°
B.130°
C.110°
D.70°
第3题图
第4题图
4.如图,已知
AB=CD,AE⊥
BD于
E,CF⊥
BD于
F,AE=CF,则图中全等三角形有(
)
A.1对
B.2对
C.3对
D.4对
5.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是(
)
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
第5题图
第6题图
6.如图,已知AE=CF,∠AFD=∠CEB,那么添加一个条件后,仍无法判定△ADF≌△CBE的是(
)
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
7.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A.两点之间的线段最短
B.长方形的四个角都是直角
C.长方形是轴对称图形
D.三角形有稳定性
8.小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )
A.①
B.②
C.③
D.①和②
9.如图,AD是△ABC的角平分线,点O在AD上,且OE⊥BC于点E,∠BAC=60°,∠C=80°,则∠EOD的度数为( )
A.20°
B.30°
C.10°
D.15°
10.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.150°
B.180°
C.210°
D.225°
11.如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是( )
A.110°
B.120°
C.130°
D.140°
12.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A.
B.
C.
D.
二、填空题(共6小题,每题4分,计24分)
13.如图,若,且,则=
.
14.如图所示,已知点A、D、B、F在一条直线上,AC=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是
.(只需填一个即可)
第14题
第15题
第16题
15.如图,点D,E分别在线段AB,AC上,BE,CD相交于点O,AE=AD,要使△ABE≌△ACD,需添加一个条件是
(只需一个即可,图中不能再添加其他点或线).
16.如图,己知AC=BD,要使△ABC≌△DCB,则只需添加一个适当的条件是
(填一个即可)
17.如图,点B在线段AE上,∠1=∠2,如果添加一个条件,即可得到△ABC≌△ABD,那么这个条件可以是
___________________(要求:不在图中添加其他辅助线,写出一个条件即可)
18.已知三角形的两边长分别为3和6,那么第三边长x的取值范围是
___________________.
三、解答题(共6小题,每题7分,共28分,)
19.如图,点A、B、C、D在同一条直线上,BE∥DF,∠A=∠F,AB=FD.
求证:AE=FC.
20.如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.
求证:△ABC≌△DEF.
21.如图,点E、F在AC上,AB∥CD,AB=CD,AE=CF.求证:△ABF≌△CDE.
22.如图,点A.B.D.E在同一直线上,AD=EB,BC∥DF,∠C=∠F.
求证:AC=EF.
答
案
部
分
一、选择题
1.D
2.B
3.C
4.C
5.
B
6.B
7.D
8.C
9.A
10.B
11.B
12.A
二、填空题
13.30°
14.BC=DE或∠A=∠F或AC∥EF
15.AB=AC或∠B=∠C或∠AEB=∠ADC
16.AB=DC或∠ACB=∠DBC
17.AC=AD或∠C=∠D或∠ABC=∠ABD或∠CBE=∠DBE
18.3<x<9
三、解答题:
19.证明:∵BE∥DF,
∴∠EBA=∠D.
在△ABE和△FDC中
∵
∴△ABE≌△FDC(ASA).
∴AE=FC.
20.证明:∵BE=CF,
∴BE+CE=CF+CE.
∴BC=EF.
∵AB∥DE,
∴∠B=∠DEF.
在△ABC和△DEF中
∵
∴△ABC≌△DEF(ASA).
21.证明:∵AB∥CD,
∴∠A=∠C.
∵AE=FC,
∴AE+EF=CF+EF.
∴AF=CE.
在△ABF和△CDE中
∵
∴△ABF≌△CDE(SAS)
22.证明:∵AD=EB,
∴AD―BD=BE―BD.
∴AB=DE.
∵BC∥DF,
∴∠CBD=∠EDF.
∴∠ABC=∠EDF
在△ABC和△EDF中
∵
∴△ABC≌△EDF(AAS)
A
B
C
C1
A1
B1
题1
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
