1.1 全等三角形同步练习（无答案）

1.1
全等三角形
同步练习
一、本课主要知识点
1、全等三角形性质：
（1）对应边相等
（2）对应角相等（3）周长相等
（4）面积相等
2、全等三角形的判定方法：
一般三角形
SAS
、ASA、
AAS、
SSS、
直角三角形
SAS
、ASA、
AAS、
SSS
、H
L
3、角平分线性质定理：角平分线上的点到这个角两边的距离相等。
逆定理：
到一个角的两边的距离相等的点在这个角的平分线上。
二、知识点练习
1、如图：AB=AC，BD=CD，若∠B=28°则∠C=
；
2、如图：EA∥DF，AE=DF，要使△AEC≌△DBF，则只要（
）
A：AB=CD
B：EC=BF
C：∠A=∠D
D：AB=BC
3、如图：在∠AOB的两边截取OA=OB，OC=OD，连接AD，BC
交于点P，则下列结论中①△AOD≌△BOC，②△APC≌△BPD，
③点P在∠AOB的平分线上。正确的是
；（填序号）
21世纪教育网
4、如图：在△ABC中，∠B=∠C=50°，D是BC的中点，DE⊥AB，
DF⊥AC，
则∠BAD=
。
5、如图,在△ABC中，∠C＝90°，AD是∠BAC的角平分线，若BC＝5㎝，BD＝3㎝，则点D到AB的距离为　　　　　.21世纪教育网
6.
如图，∠1=∠2，要使△ABE≌△ACE，还需添加的一个条件是　　　　　　(填上你认为适当的一个条件即可)
三、典型例题
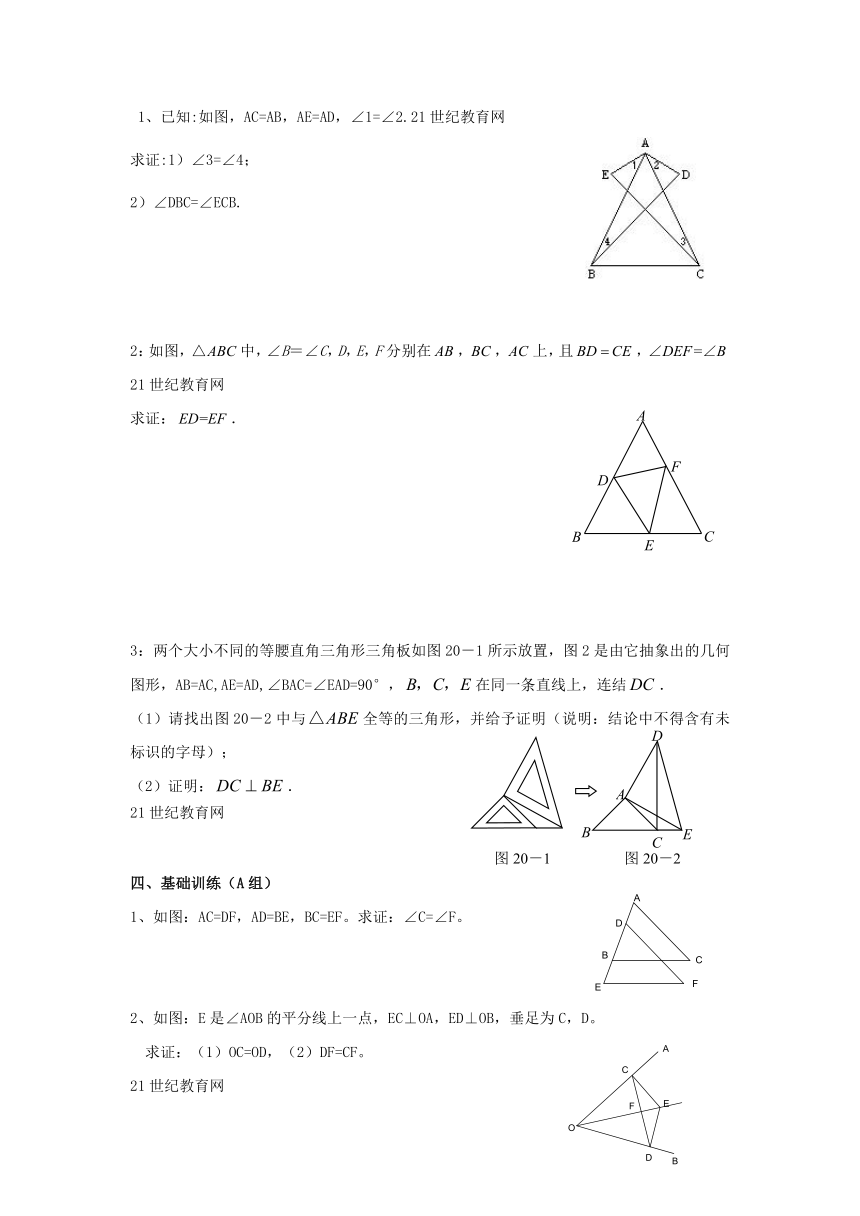
1、已知:如图，AC=AB，AE=AD，∠1=∠2.21世纪教育网
求证:1）∠3=∠4；
2）∠DBC=∠ECB.
2：如图，中，∠B＝∠C，D，E，F分别在，，上，且，
21世纪教育网
求证：．
3：两个大小不同的等腰直角三角形三角板如图20－1所示放置，图2是由它抽象出的几何图形，AB=AC,AE=AD,∠BAC=∠EAD=90°，在同一条直线上，连结．
（1）请找出图20－2中与全等的三角形，并给予证明（说明：结论中不得含有未标识的字母）；
（2）证明：．
21世纪教育网
四、基础训练（A组）
1、如图：AC=DF，AD=BE，BC=EF。求证：∠C=∠F。
2、如图：E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足为C，D。
求证：（1）OC=OD，（2）DF=CF。
21世纪教育网
3、如图：在△ABC，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F。
求证：AF平分∠BAC。
21世纪教育网21世纪教育网
4、如图，给出五个等量关系：①
②
③
④
⑤．请你以其中两个为条件，另三个中的一个为结论，推出一个正确
的结论（只需写出一种情况），并加以证明．
已知：
求证：
证明：
五、能力训练（B组）
1、如图，在∠AOB的两边OA,OB上分别取OM=ON，OD=OE，
DN和EM相交于点C．
求证：点C在∠AOB的平分线上．
2、已知：如图，在中，BE、CF分别是AC、AB两条边上的高，在BE上截取BD=AC,在CF的延长线上截取CG=AB，连接AD、AG。
求证：1）AG=AD.
2）
AD与AG的位置关系如何。
3、如图：在△ABC中，∠C=90°，AC=BC，过点C在△ABC外作直线MN，AM⊥MN于M，BN⊥MN于N。（1）求证：MN=AM+BN。21世纪教育网
（2）若过点C在△ABC内作直线MN，AM⊥MN于M，BN⊥MN于N，则AM、BN与MN之
间有什么关系？请说明理由。
六、拓展训练（C组）
1、△ABC为正三角形，点M是射线BC上任意一点，点N是射线CA上任意一点，且BM=CN，直线BN与AM相交于Q点，就下面给出的三种情况，如图8中的①②③，先用量角器分别测量∠BQM的大小，然后猜测∠BQM等于多少度．并利用图③证明你的结论．
A
C
B
D
E
A
D
E
C
B
F
图20－1
图20－2
D
C
E
A
B
A
B
C
E
D
①
②
③
图8