1.3 相似三角形 同步练习1(无答案)
文档属性
| 名称 | 1.3 相似三角形 同步练习1(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 42.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-28 00:00:00 | ||
图片预览

文档简介
1.3
相似三角形
同步练习
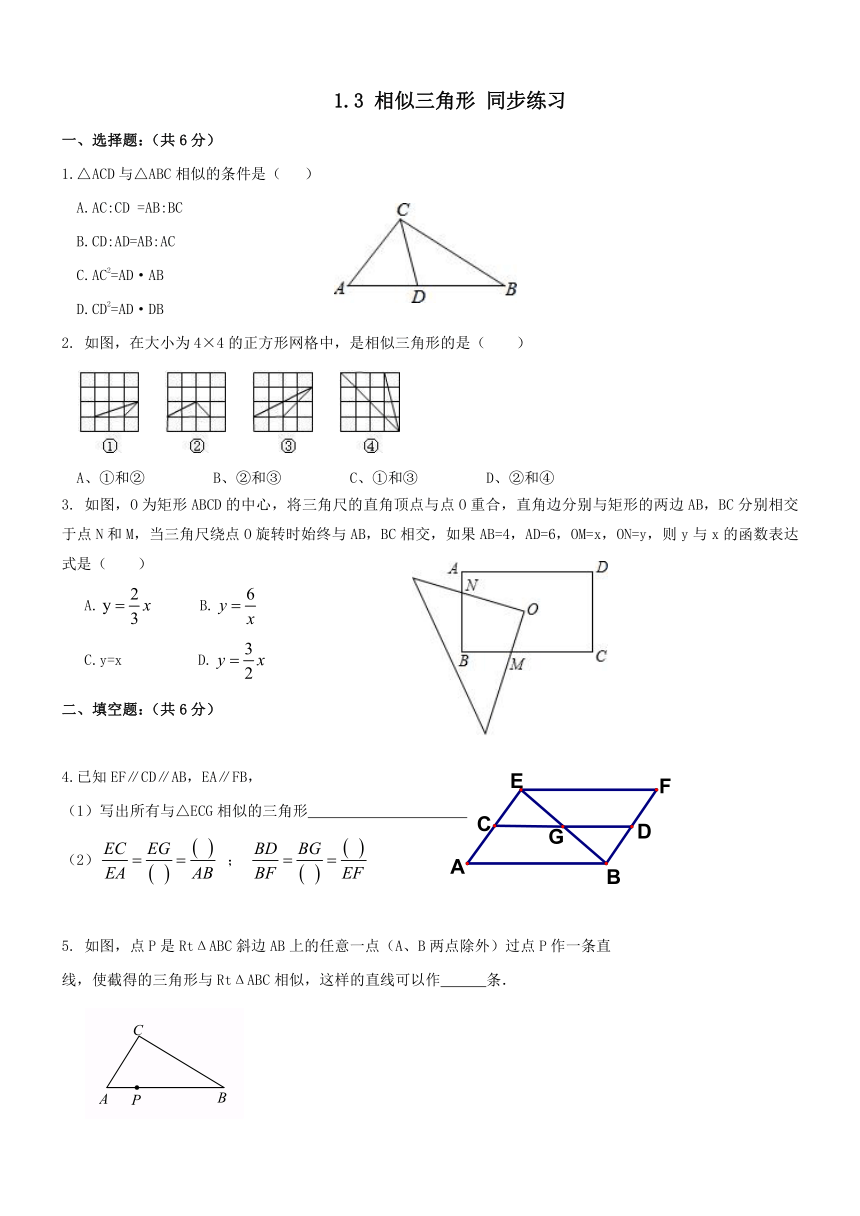
一、选择题:(共6分)
1.△ACD与△ABC相似的条件是(
)
A.AC:CD
=AB:BC
B.CD:AD=AB:AC
C.AC2=AD·AB
D.CD2=AD·DB
2.
如图,在大小为4×4的正方形网格中,是相似三角形的是( )
A、①和②
B、②和③
C、①和③
D、②和④
3.
如图,O为矩形ABCD的中心,将三角尺的直角顶点与点O重合,直角边分别与矩形的两边AB,BC分别相交于点N和M,当三角尺绕点O旋转时始终与AB,BC相交,如果AB=4,AD=6,OM=x,ON=y,则y与x的函数表达式是(
)
A.
B.
C.y=x
D.
二、填空题:(共6分)
4.已知EF∥CD∥AB,EA∥FB,
(1)写出所有与△ECG相似的三角形
(2)
;
5.
如图,点P是RtΔABC斜边AB上的任意一点(A、B两点除外)过点P作一条直
线,使截得的三角形与RtΔABC相似,这样的直线可以作 条.
6.如图,把矩形ABCD对折,折痕为MN,如果矩形DMNC与矩形ABCD相似,且AB=4
(1)AD的长=
(2)求矩形DMNC与矩形ABCD的相似比=
三、解答题:(共8分)
7.如图,在△ABC中,点D在边BC上,∠BAC=∠ADC,AC=8,BC=16,求CD的长。
8.如图,在△ABC中,已知AE=2,BE=3,DB=AE,BC=7.5
(1)△ABC∽△DBE吗?为什么?
(2)如果DE=2.5,那么AC的长是多少?
E
A
C
B
D
相似三角形
同步练习
一、选择题:(共6分)
1.△ACD与△ABC相似的条件是(
)
A.AC:CD
=AB:BC
B.CD:AD=AB:AC
C.AC2=AD·AB
D.CD2=AD·DB
2.
如图,在大小为4×4的正方形网格中,是相似三角形的是( )
A、①和②
B、②和③
C、①和③
D、②和④
3.
如图,O为矩形ABCD的中心,将三角尺的直角顶点与点O重合,直角边分别与矩形的两边AB,BC分别相交于点N和M,当三角尺绕点O旋转时始终与AB,BC相交,如果AB=4,AD=6,OM=x,ON=y,则y与x的函数表达式是(
)
A.
B.
C.y=x
D.
二、填空题:(共6分)
4.已知EF∥CD∥AB,EA∥FB,
(1)写出所有与△ECG相似的三角形
(2)
;
5.
如图,点P是RtΔABC斜边AB上的任意一点(A、B两点除外)过点P作一条直
线,使截得的三角形与RtΔABC相似,这样的直线可以作 条.
6.如图,把矩形ABCD对折,折痕为MN,如果矩形DMNC与矩形ABCD相似,且AB=4
(1)AD的长=
(2)求矩形DMNC与矩形ABCD的相似比=
三、解答题:(共8分)
7.如图,在△ABC中,点D在边BC上,∠BAC=∠ADC,AC=8,BC=16,求CD的长。
8.如图,在△ABC中,已知AE=2,BE=3,DB=AE,BC=7.5
(1)△ABC∽△DBE吗?为什么?
(2)如果DE=2.5,那么AC的长是多少?
E
A
C
B
D
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
