中考数学复习专题三:代数、三角、几何综合问题
文档属性
| 名称 | 中考数学复习专题三:代数、三角、几何综合问题 |
|
|
| 格式 | rar | ||
| 文件大小 | 71.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-19 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
中考数学复习专题3 代数、三角、几何综合问题 ( http: / / www.21cnjy.com / )
概述: ( http: / / www.21cnjy.com / )
代数、三角与几何综合题是较复杂与难度较大的问题,其中包括方程、函数、三角与几何等,内容基本上包含所有的初中数学知识,必须把以前的函数观念、方程思想、数形结合思想、转化与化归思想进行综合来解题. ( http: / / www.21cnjy.com / )
典型例题精析 ( http: / / www.21cnjy.com / )
例1.有一根直尺的短边长2cm,长边长10cm,还有一块锐角为45°的直角三角形纸板,它的斜边长12cm,如图1,将直尺的矩边DE放置与直角三角形纸板的斜边AB重合,且点D与点A重合,将直尺沿AB方向平移如图2,设平移的长度为xcm(0≤x≤10),直尺和三角形纸板的重叠部分(图中阴影部分)的面积为Scm2. ( http: / / www.21cnjy.com / )
(1)当x=0时(如图),S=________;当x=10时,S=___________;
(2)当0(3)当4( http: / / www.21cnjy.com / )
解析:(1)2;2. ( http: / / www.21cnjy.com / )
(2)在Rt△ADG中,∠A=45°, ( http: / / www.21cnjy.com / )
∴DG=AD=x. ( http: / / www.21cnjy.com / )
同理EF=AE=x+2, ( http: / / www.21cnjy.com / )
∴S梯形DEGF=(x+x+2)×2=2x+2, ( http: / / www.21cnjy.com / )
∴S=2x+2. ( http: / / www.21cnjy.com / )
(3)①当4GD=AD=x,EF=EB=12-(x+2)=10-x, ( http: / / www.21cnjy.com / )
则S△ADG=x 2,S△BEF=(10-x)2, ( http: / / www.21cnjy.com / )
而S△ABC=×12×6=36, ( http: / / www.21cnjy.com / )
∴S=36-x2-(10-x)2=-x2+10x-14, ( http: / / www.21cnjy.com / )
S=-x2+10x-14=-(x-5)2+11, ( http: / / www.21cnjy.com / )
∴当x=5(4<5<6)时,S最大值=11. ( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
②当6≤x<10时(如图6), ( http: / / www.21cnjy.com / )
BD=BG=12-x,BE=EF=10-x, ( http: / / www.21cnjy.com / )
S=(12-x+10-x)×2=22-2x, ( http: / / www.21cnjy.com / )
S随x的增大而减小,所以S≤10. ( http: / / www.21cnjy.com / )
由①、②可得,当4例2.如图所示,点O2是⊙O1上一点,⊙O2与⊙O1相交于A、D两点,BC⊥AD,垂足为D,分别交⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA的延长线于F,BO2交AD于G,连结AG. ( http: / / www.21cnjy.com / )
(1)求证:∠BGD=∠C; ( http: / / www.21cnjy.com / )
(2)若∠DO2C=45°,求证:AD=AF; ( http: / / www.21cnjy.com / )
(3)若BF=6CD,且线段BD、BF的长是关于x的方程x2-(4m+2)x+4m2+8=0的两个实数根,求BD、BF的长. ( http: / / www.21cnjy.com / )
解析:(1)∵BC⊥AD于D, ( http: / / www.21cnjy.com / )
∴∠BDA=∠CDA=90°, ( http: / / www.21cnjy.com / )
∴AB、AC分别为⊙O1、⊙O2的直径. ( http: / / www.21cnjy.com / )
∵∠2=∠3,∠BGD+∠2=90°,∠C+∠3=90°, ( http: / / www.21cnjy.com / )
∴∠BGD=∠C. ( http: / / www.21cnjy.com / )
(2)∵∠DO2C=45°,∴∠ABD=45°,∵O2D=O2C, ( http: / / www.21cnjy.com / )
∴∠C=∠O2DC=(180°-∠DO2C)=67.5°, ( http: / / www.21cnjy.com / )
∴∠4=22.5°, ∵∠O2DC=∠ABD+∠F, ( http: / / www.21cnjy.com / )
∴∠F=∠4=22.5°,∴AD=AF. ( http: / / www.21cnjy.com / )
(3)∵BF=6CD,∴设CD=k,则BF=6k. ( http: / / www.21cnjy.com / )
连结AE,则AE⊥AD,∴AE∥BC, ( http: / / www.21cnjy.com / )
∴ ∴AE·BF=BD·AF. ( http: / / www.21cnjy.com / )
又∵在△AO2E和△DO2C中,AO2=DO2 ( http: / / www.21cnjy.com / )
∠AO2E=∠DO2C, O2E=O2C, ( http: / / www.21cnjy.com / )
∴△AO2E≌△DO2C,∴AE=CD=k, ( http: / / www.21cnjy.com / )
∴6k2=BD·AF=(BC-CD)(BF-AB). ( http: / / www.21cnjy.com / )
∵∠BO2A=90°,O2A=O2C,∴BC=AB. ( http: / / www.21cnjy.com / )
∴6k2=(BC-k)(6k-BC).∴BC2-7kBC+12k2=0, ( http: / / www.21cnjy.com / )
解得:BC=3k或BC=4k. ( http: / / www.21cnjy.com / )
当BC=3k,BD=2k. ( http: / / www.21cnjy.com / )
∵BD、BF的长是关于x的方程x2-(4m+2)x+4m2+8=0的两个实数根. ( http: / / www.21cnjy.com / )
∴由根与系数的关系知:BD+BF=2k+6k=8k=4m+2. ( http: / / www.21cnjy.com / )
整理,得:4m2-12m+29=0. ( http: / / www.21cnjy.com / )
∵△=(-12)2-4×4×29=-320<0,此方程无实数根. ( http: / / www.21cnjy.com / )
∴BC=3k(舍). ( http: / / www.21cnjy.com / )
当BC=4k时,BD=3k. ( http: / / www.21cnjy.com / )
∴3k+6k=4m+2,18k2=4m2+8,整理, ( http: / / www.21cnjy.com / )
得:m2-8m+16=0, ( http: / / www.21cnjy.com / )
解得:m1=m2=4, ( http: / / www.21cnjy.com / )
∴原方程可化为x2-18x+72=0, ( http: / / www.21cnjy.com / )
解得:x1=6,x2=12, ∴BD=6,BF=12. ( http: / / www.21cnjy.com / )
中考样题训练 ( http: / / www.21cnjy.com / )
1.已知抛物线y=-x2+(k+1)x+3,当x<1时,y随着x的增大而增大,当x>1时,y随x的增大而减小. ( http: / / www.21cnjy.com / )
(1)求k的值及抛物线的解析式; ( http: / / www.21cnjy.com / )
(2)设抛物线与x轴交于A、B两点(A在B的左边),抛物线的顶点为P,试求出A、B、P三点的坐标,并在直角坐标系中画出这条抛物线; ( http: / / www.21cnjy.com / )
(3)求经过P、A、B三点的圆的圆心O′的坐标; ( http: / / www.21cnjy.com / )
(4)设点G(0,m)是y轴上的动点. ( http: / / www.21cnjy.com / )
①当点G运动到何处时,直线BG是⊙O′的切线?并求出此时直线BG的解析式. ( http: / / www.21cnjy.com / )
②若直线BG与⊙O相交,且另一个交点为D,当m满足什么条件时,点D在x轴的下方? ( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
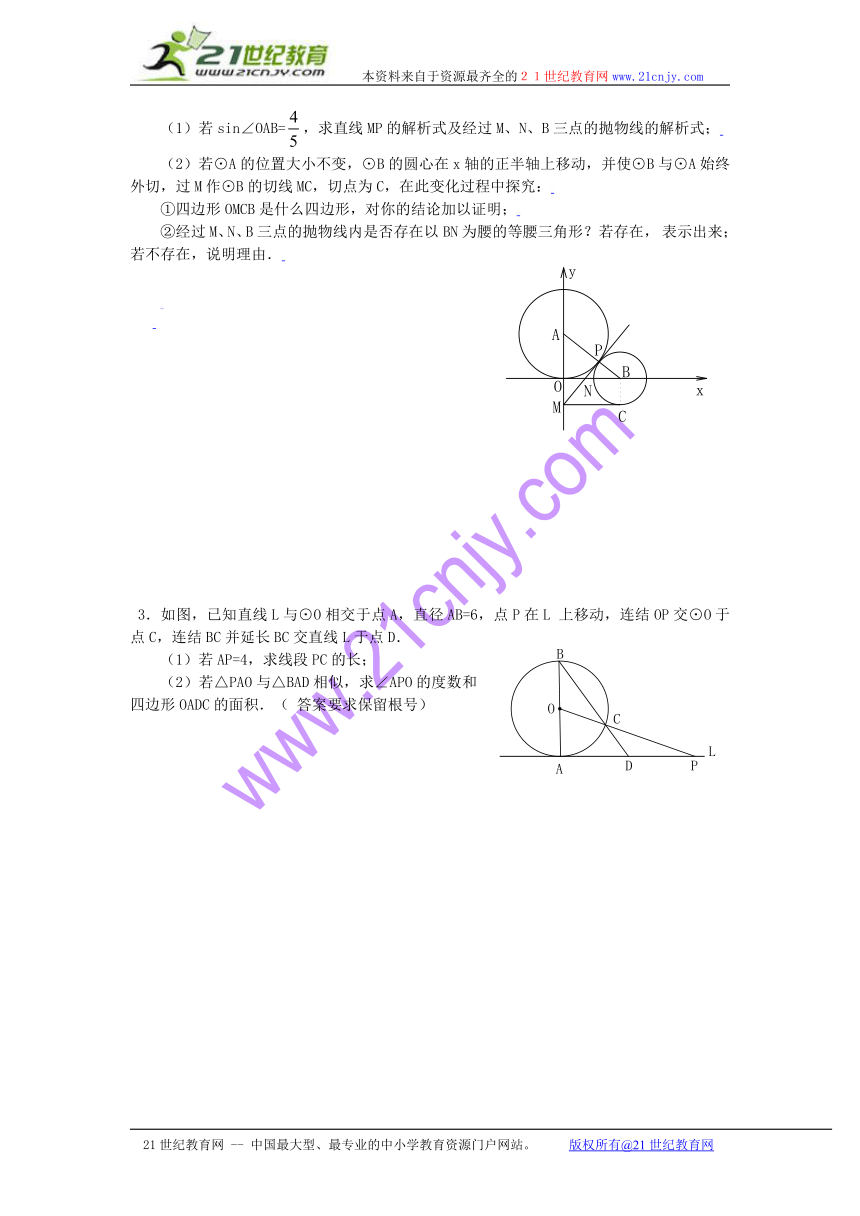
2.如图,已知圆心A(0,3),⊙A与x轴相切,⊙B的圆心在x轴的正半轴上,且⊙B与⊙A外切于点P,两圆的公切线MP交y轴于点M,交x轴于点N. ( http: / / www.21cnjy.com / )
(1)若sin∠OAB=,求直线MP的解析式及经过M、N、B三点的抛物线的解析式; ( http: / / www.21cnjy.com / )
(2)若⊙A的位置大小不变,⊙B的圆心在x轴的正半轴上移动,并使⊙B与⊙A始终外切,过M作⊙B的切线MC,切点为C,在此变化过程中探究: ( http: / / www.21cnjy.com / )
①四边形OMCB是什么四边形,对你的结论加以证明; ( http: / / www.21cnjy.com / )
②经过M、N、B三点的抛物线内是否存在以BN为腰的等腰三角形?若存在,表示出来;若不存在,说明理由. ( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
3.如图,已知直线L与⊙O相交于点A,直径AB=6,点P在L上移动,连结OP交⊙O于点C,连结BC并延长BC交直线L于点D.
(1)若AP=4,求线段PC的长;
(2)若△PAO与△BAD相似,求∠APO的度数和四边形OADC的面积.(答案要求保留根号)
考前热身训练
1.如图,已知A为∠POQ的边OQ上一点,以A为顶点的∠MAN的两边分别交射线OP于M、N两点,且∠MAN=∠POQ=α(α为锐角),当∠MAN为以点A为旋转中心,AM边从与AO重合的位置开始,按逆时针方向旋转(∠MAN保持不变)时,M、N两点在射线OP上同时以不同的速度向右平行移动.设OM=x,ON=y(y>x≥0),△AOM的面积为S,若cosα、OA是方程2z2-5z+2=0的两个根.
(1)当∠MAN旋转30°(即∠OAM=30°)时,求点N移动的距离;
(2)求证:AN2=ON·MN;
(3)求y与x之间的函数关系式及自变量量x的取值范围;
(4)试写出S随x变化的函数关系式,并确定S的取值范围.
2.如图,已知P、A、B是x轴上的三点,点A的坐标为(-1,0),点B的坐标为(3,0),且PA:AB=1:2,以AB为直径画⊙M交y轴的正半轴于点C.
(1)求证:PC是⊙M的切线;
(2)在x轴上是否存在这样的点Q,使得直线QC与过A、C、B三点的抛物线只有一个交点?若存在,求点Q的坐标,若不存在,请说明理由;
(3)画⊙N,使得圆心N在x轴的负半轴上,⊙N与⊙M外切,且与直线PC相切于D,问将过A、C、B三点的抛物线平移后,能否同时经过P、D、A三点?为什么?
答案:
中考样题看台
1.(1)k=1,抛物线解析式y=-x2+2x+3
(2)A(-1,0),B(3,0),C(1,4)
(3)∵⊙O′过A、B两点,
∴O′在AB的垂直平分线上,即在抛物线的对称轴上,
设抛物线的对称轴交x轴于M,交⊙O′于N,
则有MP×MN=MA×MB,4MN=2×2,
∴MN=1,PN=5,O′P=∴O′点在x轴上方,∴O′M=,∴O′(1,).
(4)①过B点作⊙O′的切线交y轴于点G,直线BO′交y轴于点E,
可求出直线BO′的解析式为,y=-x+,
∴E(0,),∵BG是⊙O′的切线,BO⊥EG,
∴BO=OE×OG,∴OG=4,∴G(0,-4),
求出直线BG的解析式为y=x-4.
②-42.(1)在Rt△AOB中,∵OA=3,sin∠OAB=,cos∠OAB=,
∴AB=5,OB=4,BP=5-3=2.
在Rt△APM中,=cos∠OAB=,
∴AM=5,OM=2,∴点M(0,-2),
又△NPB∽△AOB,∴,
∴BN=,∴ON=,∴点B(,0),
设MP的解析式为y=kx+b,∵MP经过M、N两点,
∴MP的解析式为y=x-2,
设过M、N、B的抛物线解析式为y=a(x-)(x-4)
且点M(0,-2)在其上,可得a=-,即y=-x2+x-2.
(2)①四边形OMCB是矩形.
证明:在⊙A不动,⊙B运动变化过程中,
恒有∠BAO=∠MAP,OA=AP,∠AOB=∠APM=90°,
∴△AOB≌△APM,
∴OB=PM,AB=AM,
∴PB=OM,
而PB=BC,∴OM=BC,
由切线长定理知MC=MP,∴MC=OB,
∴四边形MOBC是平行四边形,
又∵∠MOB=90°,
∴四边形MOBC是矩形.
②存在,由上证明可知,Rt△MON≌Rt△BPN,
∴BN=MN.
因此在过M、N、B三点的抛物线内有以BN为腰的等腰三角形MNB存在,
由抛物线的轴对称性可知,在抛物线上必有一点M′与M关于其对称轴对称,
∴BN=BM′,这样得到满足条件的三角形有两个,△MNB和△M′NB.
3.(1)∵L与⊙O相切于点A,
∴∠4=90°,∴OP2=OA2+AP2,
∵OB=OC=AB=3,AP=4,
∴OP2=32+42,∴OP=5,
∴PC=5-3=2.
(2)∵△PAO∽△BAD,且∠1>∠2,∠4=90°,
∴∠2=∠APO,∴OB=OC,∴∠2=∠3
∵∠1=∠2+∠3,∴∠2=2∠2=2∠APO
∴∠4=90°,∴∠1+∠APO=90°
∴3∠APO=90°,∴∠APO=30°.
在Rt△BAD中,∠2=∠APO=30°.
∴AD=6sin30°=6×=2.
过点O作OE⊥BC于点E
∵∠2=30°,BO=3,
∴OE=,BE=3×cos30°=,
∴BC=2BE=3,
∴S四边形OADC=S△BAD-S△BOC=AB·AD
=BC·OE=×6×2-×3×=6-= .
考前热身训练
1.(1)易知OA=2,cosα=,∠POQ=∠MAN=60°,
∴初始状态时,△AON为等边三角形,
∴ON=OA=2,当AM旋转到AM′时,点N移动到N′,
∵∠OAM′=30°,∠POQ=∠M′AN′=60°,
∴∠M′N′A=30°,在Rt△OAN中,ON′=2AO=4,
∴NN′=ON′-ON=2,∴点N移动的距离为2.
(2)易知△OAN∽△AMN,∴AN2=ON·MN.
(3)∵MN=y-x,∴AN2=y2-xy,
过A点作AD⊥OP,垂足为D,可得OD=1,AD=,
∴DN=ON-OD=y-1,
在Rt△AND中,AN2=AD2+DN2=y2-2y+4,
∴y2-xy=y2-2y+4,即y=.
∴y>0,∴2-x>0,即x<2,
又∵x≥0,∴x的取值范围是:0≤x<2.
(4)S=·OM·AD=x,
∵S是x的正比例函数,且比例系数>0,
∴0≤S<·2.即0≤S<
2.(1)易知⊙M半径为2,设PA=x,则x:4=1:2x=2,
由相交弦定理推论得OC=OA.OB=1×3,
∴OC=,∴PC2=PO2+OC2=32+()2=12,
PM2=42=16,MC2=22=4,
∴PM2=PC2+MC2,∴∠PCM=90°.
(2)易知过A、C、B三点的抛物线的解析式为y=-(x+1)(x-3),
假设满足条件的Q点存在,坐标为(m,0),直线QC的解析式为y=-x+,
∵直线QC与抛物线只有一个公共点,
∴方程-(x+1)(x-3)=-x+有相等的实根,
∴(2+)2=0,∴m=-,即满足条件的Q点存在,坐标为(-,0);
(3)连结DN,作DH⊥PN,垂足为H,设⊙N的半径为r,则∵ND⊥PC,
∴ND∥MC,∴,∴,
∴r=,∵DN2=NH·NP,
∴()2=NH·(2-),∴NH=,
∴DH==,∴D(-2,).
∵抛物线y=-(x+1)(x-3)平移,使其经过P、A两点的抛物线的解析式为
y=-(x+1)(x+3)
又经验证D是该抛物线上的点,
∴将过A、C、B三点的抛物线平移后能同时经过P、D、A三点.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
中考数学复习专题3 代数、三角、几何综合问题 ( http: / / www.21cnjy.com / )
概述: ( http: / / www.21cnjy.com / )
代数、三角与几何综合题是较复杂与难度较大的问题,其中包括方程、函数、三角与几何等,内容基本上包含所有的初中数学知识,必须把以前的函数观念、方程思想、数形结合思想、转化与化归思想进行综合来解题. ( http: / / www.21cnjy.com / )
典型例题精析 ( http: / / www.21cnjy.com / )
例1.有一根直尺的短边长2cm,长边长10cm,还有一块锐角为45°的直角三角形纸板,它的斜边长12cm,如图1,将直尺的矩边DE放置与直角三角形纸板的斜边AB重合,且点D与点A重合,将直尺沿AB方向平移如图2,设平移的长度为xcm(0≤x≤10),直尺和三角形纸板的重叠部分(图中阴影部分)的面积为Scm2. ( http: / / www.21cnjy.com / )
(1)当x=0时(如图),S=________;当x=10时,S=___________;
(2)当0
解析:(1)2;2. ( http: / / www.21cnjy.com / )
(2)在Rt△ADG中,∠A=45°, ( http: / / www.21cnjy.com / )
∴DG=AD=x. ( http: / / www.21cnjy.com / )
同理EF=AE=x+2, ( http: / / www.21cnjy.com / )
∴S梯形DEGF=(x+x+2)×2=2x+2, ( http: / / www.21cnjy.com / )
∴S=2x+2. ( http: / / www.21cnjy.com / )
(3)①当4
则S△ADG=x 2,S△BEF=(10-x)2, ( http: / / www.21cnjy.com / )
而S△ABC=×12×6=36, ( http: / / www.21cnjy.com / )
∴S=36-x2-(10-x)2=-x2+10x-14, ( http: / / www.21cnjy.com / )
S=-x2+10x-14=-(x-5)2+11, ( http: / / www.21cnjy.com / )
∴当x=5(4<5<6)时,S最大值=11. ( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
②当6≤x<10时(如图6), ( http: / / www.21cnjy.com / )
BD=BG=12-x,BE=EF=10-x, ( http: / / www.21cnjy.com / )
S=(12-x+10-x)×2=22-2x, ( http: / / www.21cnjy.com / )
S随x的增大而减小,所以S≤10. ( http: / / www.21cnjy.com / )
由①、②可得,当4
(1)求证:∠BGD=∠C; ( http: / / www.21cnjy.com / )
(2)若∠DO2C=45°,求证:AD=AF; ( http: / / www.21cnjy.com / )
(3)若BF=6CD,且线段BD、BF的长是关于x的方程x2-(4m+2)x+4m2+8=0的两个实数根,求BD、BF的长. ( http: / / www.21cnjy.com / )
解析:(1)∵BC⊥AD于D, ( http: / / www.21cnjy.com / )
∴∠BDA=∠CDA=90°, ( http: / / www.21cnjy.com / )
∴AB、AC分别为⊙O1、⊙O2的直径. ( http: / / www.21cnjy.com / )
∵∠2=∠3,∠BGD+∠2=90°,∠C+∠3=90°, ( http: / / www.21cnjy.com / )
∴∠BGD=∠C. ( http: / / www.21cnjy.com / )
(2)∵∠DO2C=45°,∴∠ABD=45°,∵O2D=O2C, ( http: / / www.21cnjy.com / )
∴∠C=∠O2DC=(180°-∠DO2C)=67.5°, ( http: / / www.21cnjy.com / )
∴∠4=22.5°, ∵∠O2DC=∠ABD+∠F, ( http: / / www.21cnjy.com / )
∴∠F=∠4=22.5°,∴AD=AF. ( http: / / www.21cnjy.com / )
(3)∵BF=6CD,∴设CD=k,则BF=6k. ( http: / / www.21cnjy.com / )
连结AE,则AE⊥AD,∴AE∥BC, ( http: / / www.21cnjy.com / )
∴ ∴AE·BF=BD·AF. ( http: / / www.21cnjy.com / )
又∵在△AO2E和△DO2C中,AO2=DO2 ( http: / / www.21cnjy.com / )
∠AO2E=∠DO2C, O2E=O2C, ( http: / / www.21cnjy.com / )
∴△AO2E≌△DO2C,∴AE=CD=k, ( http: / / www.21cnjy.com / )
∴6k2=BD·AF=(BC-CD)(BF-AB). ( http: / / www.21cnjy.com / )
∵∠BO2A=90°,O2A=O2C,∴BC=AB. ( http: / / www.21cnjy.com / )
∴6k2=(BC-k)(6k-BC).∴BC2-7kBC+12k2=0, ( http: / / www.21cnjy.com / )
解得:BC=3k或BC=4k. ( http: / / www.21cnjy.com / )
当BC=3k,BD=2k. ( http: / / www.21cnjy.com / )
∵BD、BF的长是关于x的方程x2-(4m+2)x+4m2+8=0的两个实数根. ( http: / / www.21cnjy.com / )
∴由根与系数的关系知:BD+BF=2k+6k=8k=4m+2. ( http: / / www.21cnjy.com / )
整理,得:4m2-12m+29=0. ( http: / / www.21cnjy.com / )
∵△=(-12)2-4×4×29=-320<0,此方程无实数根. ( http: / / www.21cnjy.com / )
∴BC=3k(舍). ( http: / / www.21cnjy.com / )
当BC=4k时,BD=3k. ( http: / / www.21cnjy.com / )
∴3k+6k=4m+2,18k2=4m2+8,整理, ( http: / / www.21cnjy.com / )
得:m2-8m+16=0, ( http: / / www.21cnjy.com / )
解得:m1=m2=4, ( http: / / www.21cnjy.com / )
∴原方程可化为x2-18x+72=0, ( http: / / www.21cnjy.com / )
解得:x1=6,x2=12, ∴BD=6,BF=12. ( http: / / www.21cnjy.com / )
中考样题训练 ( http: / / www.21cnjy.com / )
1.已知抛物线y=-x2+(k+1)x+3,当x<1时,y随着x的增大而增大,当x>1时,y随x的增大而减小. ( http: / / www.21cnjy.com / )
(1)求k的值及抛物线的解析式; ( http: / / www.21cnjy.com / )
(2)设抛物线与x轴交于A、B两点(A在B的左边),抛物线的顶点为P,试求出A、B、P三点的坐标,并在直角坐标系中画出这条抛物线; ( http: / / www.21cnjy.com / )
(3)求经过P、A、B三点的圆的圆心O′的坐标; ( http: / / www.21cnjy.com / )
(4)设点G(0,m)是y轴上的动点. ( http: / / www.21cnjy.com / )
①当点G运动到何处时,直线BG是⊙O′的切线?并求出此时直线BG的解析式. ( http: / / www.21cnjy.com / )
②若直线BG与⊙O相交,且另一个交点为D,当m满足什么条件时,点D在x轴的下方? ( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
2.如图,已知圆心A(0,3),⊙A与x轴相切,⊙B的圆心在x轴的正半轴上,且⊙B与⊙A外切于点P,两圆的公切线MP交y轴于点M,交x轴于点N. ( http: / / www.21cnjy.com / )
(1)若sin∠OAB=,求直线MP的解析式及经过M、N、B三点的抛物线的解析式; ( http: / / www.21cnjy.com / )
(2)若⊙A的位置大小不变,⊙B的圆心在x轴的正半轴上移动,并使⊙B与⊙A始终外切,过M作⊙B的切线MC,切点为C,在此变化过程中探究: ( http: / / www.21cnjy.com / )
①四边形OMCB是什么四边形,对你的结论加以证明; ( http: / / www.21cnjy.com / )
②经过M、N、B三点的抛物线内是否存在以BN为腰的等腰三角形?若存在,表示出来;若不存在,说明理由. ( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
3.如图,已知直线L与⊙O相交于点A,直径AB=6,点P在L上移动,连结OP交⊙O于点C,连结BC并延长BC交直线L于点D.
(1)若AP=4,求线段PC的长;
(2)若△PAO与△BAD相似,求∠APO的度数和四边形OADC的面积.(答案要求保留根号)
考前热身训练
1.如图,已知A为∠POQ的边OQ上一点,以A为顶点的∠MAN的两边分别交射线OP于M、N两点,且∠MAN=∠POQ=α(α为锐角),当∠MAN为以点A为旋转中心,AM边从与AO重合的位置开始,按逆时针方向旋转(∠MAN保持不变)时,M、N两点在射线OP上同时以不同的速度向右平行移动.设OM=x,ON=y(y>x≥0),△AOM的面积为S,若cosα、OA是方程2z2-5z+2=0的两个根.
(1)当∠MAN旋转30°(即∠OAM=30°)时,求点N移动的距离;
(2)求证:AN2=ON·MN;
(3)求y与x之间的函数关系式及自变量量x的取值范围;
(4)试写出S随x变化的函数关系式,并确定S的取值范围.
2.如图,已知P、A、B是x轴上的三点,点A的坐标为(-1,0),点B的坐标为(3,0),且PA:AB=1:2,以AB为直径画⊙M交y轴的正半轴于点C.
(1)求证:PC是⊙M的切线;
(2)在x轴上是否存在这样的点Q,使得直线QC与过A、C、B三点的抛物线只有一个交点?若存在,求点Q的坐标,若不存在,请说明理由;
(3)画⊙N,使得圆心N在x轴的负半轴上,⊙N与⊙M外切,且与直线PC相切于D,问将过A、C、B三点的抛物线平移后,能否同时经过P、D、A三点?为什么?
答案:
中考样题看台
1.(1)k=1,抛物线解析式y=-x2+2x+3
(2)A(-1,0),B(3,0),C(1,4)
(3)∵⊙O′过A、B两点,
∴O′在AB的垂直平分线上,即在抛物线的对称轴上,
设抛物线的对称轴交x轴于M,交⊙O′于N,
则有MP×MN=MA×MB,4MN=2×2,
∴MN=1,PN=5,O′P=
(4)①过B点作⊙O′的切线交y轴于点G,直线BO′交y轴于点E,
可求出直线BO′的解析式为,y=-x+,
∴E(0,),∵BG是⊙O′的切线,BO⊥EG,
∴BO=OE×OG,∴OG=4,∴G(0,-4),
求出直线BG的解析式为y=x-4.
②-4
∴AB=5,OB=4,BP=5-3=2.
在Rt△APM中,=cos∠OAB=,
∴AM=5,OM=2,∴点M(0,-2),
又△NPB∽△AOB,∴,
∴BN=,∴ON=,∴点B(,0),
设MP的解析式为y=kx+b,∵MP经过M、N两点,
∴MP的解析式为y=x-2,
设过M、N、B的抛物线解析式为y=a(x-)(x-4)
且点M(0,-2)在其上,可得a=-,即y=-x2+x-2.
(2)①四边形OMCB是矩形.
证明:在⊙A不动,⊙B运动变化过程中,
恒有∠BAO=∠MAP,OA=AP,∠AOB=∠APM=90°,
∴△AOB≌△APM,
∴OB=PM,AB=AM,
∴PB=OM,
而PB=BC,∴OM=BC,
由切线长定理知MC=MP,∴MC=OB,
∴四边形MOBC是平行四边形,
又∵∠MOB=90°,
∴四边形MOBC是矩形.
②存在,由上证明可知,Rt△MON≌Rt△BPN,
∴BN=MN.
因此在过M、N、B三点的抛物线内有以BN为腰的等腰三角形MNB存在,
由抛物线的轴对称性可知,在抛物线上必有一点M′与M关于其对称轴对称,
∴BN=BM′,这样得到满足条件的三角形有两个,△MNB和△M′NB.
3.(1)∵L与⊙O相切于点A,
∴∠4=90°,∴OP2=OA2+AP2,
∵OB=OC=AB=3,AP=4,
∴OP2=32+42,∴OP=5,
∴PC=5-3=2.
(2)∵△PAO∽△BAD,且∠1>∠2,∠4=90°,
∴∠2=∠APO,∴OB=OC,∴∠2=∠3
∵∠1=∠2+∠3,∴∠2=2∠2=2∠APO
∴∠4=90°,∴∠1+∠APO=90°
∴3∠APO=90°,∴∠APO=30°.
在Rt△BAD中,∠2=∠APO=30°.
∴AD=6sin30°=6×=2.
过点O作OE⊥BC于点E
∵∠2=30°,BO=3,
∴OE=,BE=3×cos30°=,
∴BC=2BE=3,
∴S四边形OADC=S△BAD-S△BOC=AB·AD
=BC·OE=×6×2-×3×=6-= .
考前热身训练
1.(1)易知OA=2,cosα=,∠POQ=∠MAN=60°,
∴初始状态时,△AON为等边三角形,
∴ON=OA=2,当AM旋转到AM′时,点N移动到N′,
∵∠OAM′=30°,∠POQ=∠M′AN′=60°,
∴∠M′N′A=30°,在Rt△OAN中,ON′=2AO=4,
∴NN′=ON′-ON=2,∴点N移动的距离为2.
(2)易知△OAN∽△AMN,∴AN2=ON·MN.
(3)∵MN=y-x,∴AN2=y2-xy,
过A点作AD⊥OP,垂足为D,可得OD=1,AD=,
∴DN=ON-OD=y-1,
在Rt△AND中,AN2=AD2+DN2=y2-2y+4,
∴y2-xy=y2-2y+4,即y=.
∴y>0,∴2-x>0,即x<2,
又∵x≥0,∴x的取值范围是:0≤x<2.
(4)S=·OM·AD=x,
∵S是x的正比例函数,且比例系数>0,
∴0≤S<·2.即0≤S<
2.(1)易知⊙M半径为2,设PA=x,则x:4=1:2x=2,
由相交弦定理推论得OC=OA.OB=1×3,
∴OC=,∴PC2=PO2+OC2=32+()2=12,
PM2=42=16,MC2=22=4,
∴PM2=PC2+MC2,∴∠PCM=90°.
(2)易知过A、C、B三点的抛物线的解析式为y=-(x+1)(x-3),
假设满足条件的Q点存在,坐标为(m,0),直线QC的解析式为y=-x+,
∵直线QC与抛物线只有一个公共点,
∴方程-(x+1)(x-3)=-x+有相等的实根,
∴(2+)2=0,∴m=-,即满足条件的Q点存在,坐标为(-,0);
(3)连结DN,作DH⊥PN,垂足为H,设⊙N的半径为r,则∵ND⊥PC,
∴ND∥MC,∴,∴,
∴r=,∵DN2=NH·NP,
∴()2=NH·(2-),∴NH=,
∴DH==,∴D(-2,).
∵抛物线y=-(x+1)(x-3)平移,使其经过P、A两点的抛物线的解析式为
y=-(x+1)(x+3)
又经验证D是该抛物线上的点,
∴将过A、C、B三点的抛物线平移后能同时经过P、D、A三点.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
